发展学生思维能力 提升数学解题效率

赵静静

(蒙城县庄子中学,安徽 亳州 233500)

与小学阶段相比,初中数学知识相对抽象复杂,是学生学习的难点.纵观初中数学解题教学现状,普遍存在学生基础知识薄弱、兴趣不佳、抽象概括能力不足以及教师教学方式单一等问题,这些问题严重影响了解题教学质量.为此,数学教师应在新课程标准指导下,结合学生学情从多方面优化解题教学,切实提升解题教学效果,深化学生对所学知识理解,使学生养成良好的解题习惯,提高学生解题水平[1].

1 巧用数学模型思想,提升解题效率

1.1 构建函数模型解题

在初中数学教学中,“函数”是重要的教学内容,它能够反应出现实生活中变量之间的变化关系,在现实生活中有着广泛的应用.如计划决策、居民用电以及投资理财等,均可以构建相应的函数模型,完成问题的解决[2].

例1 某个城市为了鼓励居民节约用水,采取分段计费的方式,月用水量不超过20立方米时,按照每立方米2元收费,月用水量超过20立方米时,其中的20立方米依然按照2元每立方米计算,超出的部分按照2.6元每立方米计费.某学生家第一季度的用水情况如表1所示:

表1 第一季度用水情况表

求解这名学生家本季度一共需要交多少水费?

解析根据题意可知,采取分段计费的方式收取水费,需分别构建模型,根据用水量的不同,确定收费标准.因此,可以构建分段函数模型.假设家庭的月用水量为x立方米,当用水量不超过20立方米时,需要交的水费为y1元,超过20立方米,需要交的水费为y2元,本季度总水费时y元,则y1=2x(0≤x≤20),y2=20×2+2.6(x-20)=2.6x-12(x>20),y是三个月水费之和.显然,对每个月的水费进行计算,最终完成本季度水费的计算.

对于分段、分类型等问题,可以通过构建分段函数模型进行解题.在分段函数模型中,需要明确每个分段函数的定义域,根据题意准确构建模型.

1.2 构建几何模型解题

几何模型是中考数学中考查的重要内容,学生需熟悉并且灵活利用几何模型解决问题,对学生空间想象能力要求较高.在数学教学中,教师需引导学生根据题目类型,构建相应的几何模型,完成数学问题的解答,提高解题效率[3].

例2 如图1所示,△ABC是等边三角形,AB=6,N是AB上的任意一点,∠BAC的平分线与BC相较于点D,M是AD上的动点,连接MB,MN,求MB+MN的最小值.

图1 例2题图

解析本题涉及到动点、最小值等知识,需要引导学生进行转化,将其转化成“两点之间线段最短”问题进行解决.为此,教师可以让学生思考“将军饮马”模型,让学生对问题进行思考和解答.找出点B关于定直线AD的对称点,即点C.当C,M,N三点在同一条直线上,且CN⊥AB时,MB+MN的值最小.如图1,过C点作CE⊥AB,垂足为E,则MB+MN的最小值等于线段CE的长.

“将军饮马”问题是初中数学中常见的几何模型,通过这样的模型构建与转化,完成了问题解答.在数学教学中,教师还应引导学生关注其他几何模型,为问题解决指引方向.

1.3 构建方程、不等式模型解题

方程、不等式是将现实问题数学化的有效模型.利用其解决问题的基本思路是:根据题意寻找相等或不等关系,然后,通过方程或不等式解决数学问题.现实生活中有很多相等或不等关系,如增长率、打折销售以及工程问题等,利用模型思想,能够准确找出其中的数量关系,设定合适的未知数,利用未知数表示数量关系,构建相应的方程或者不等式模型,从而有效解决问题[4].

例3某个商店计划用1 200元购进A、B两种型号的羽毛球拍,其中A型号的羽毛球拍进价是每副12元,B型号羽毛球拍的进价是每副10元,在销售时,A的售价是15元/副,B的售价是12元/副,全部售完,获利是270元.①求解A、B两种型号的羽毛球拍各进了多少副?②如果该商店以原进价再次购进A、B两种型号的羽毛球拍,A型号羽毛球拍数量不变,B型号羽毛球拍数量是第一次的两倍,B型号羽毛球拍按照原来的售价销售,A型号羽毛球拍则降价销售,当两种羽毛球拍销售完,想要使得再次购进的羽毛球拍利润不少于340元,A型号羽毛球拍最低售价是每副多少元?

根据数量关系,构建方程模型,可求出购进两种型号的羽毛球拍的数量.在完成问题①的解答之后,对问题②进行分析,根据题意构建相应的不等式模型,完成求解.

2 巧借数学转化思想,提升解题能力

培养学生思维能力是数学学科的重要目标,尤其各种数学思想在提升教学效率和学生数学核心素养方面发挥着不可小觑作用.学生在小学阶段已经历数学学习并感悟数学学科的抽象化特征,升至初中阶段需着重培养思维能力,养成良好思维习惯.转化思想是初中数学重要思想之一,简言之,运用转化思想简化学生理解知识和解题难度,提升学习效率[5].从另一角度剖析,转化思想即从不同角度将同一数学知识或问题转化为易被学生理解的表达形式,激发学生深层次探究数学知识的欲望,最重要是帮助学生理解和掌握数学元素之间的逻辑关系,在解题中对所学知识展开深入思考,提升数学素养.

教师可从两个方面为学生渗透数学思想:其一,换元转化.该方式旨在化繁为简,以变量问题为例,运用转化思想可多个变量问题转为一个变量问题,减小解题难度.同时,该方式还能减少计算量,将无从下手的问题转至常规问题后再进行解答,增强分析与解答问题能力.

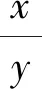
由此可以看出,转化思想的应用有效降低了问题的难度,当学生发现转化思想的独特与便利之处后就可激发潜在持续学习数学兴趣,在后续学习和解题中遇到相同问题也可顺利解决.

其二,化同为殊.纵观初中几何问题,命题者给出的已知条件与所求量之间的逻辑关系较为隐蔽,学生需深入思考后通过添加辅助线解答,使已知条件与所求量之间的逻辑关系外显化,拓宽学生解题思维,提升学生解题能力.

例5在△BCD中,∠C=60°,BC长度为6,BD的长度为8,求三角形的边CD的长度.

如果学生运用初中数学知识解答上述题目则较为复杂,尤其题目可用信息相对较少,此时可通过添加辅助线,化难为易,使问题顺利解决.

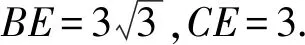
由此可见,在解答几何问题时,添加辅助线可降低问题难度,即将多个难度较大的问题转为较为简单的小问题后再运用所学知识解决,提升解题能力.

3 巧用数学化归思想,提升解题能力

顾名思义,“化归”为转化与归纳简称.数学中的化归思想是指将较为复杂或抽象的问题转化为较易被学生解答的简单问题,或将未知转为已知,将分式方程转化为整式方程,将四边形问题转化为三角形问题,等等.化归思想作为初中数学解题不可缺少的数学思想,在解决相关问题时运用其分析问题,能有效提升学生解题效率.纵观初中数学解题,有很多方面都体现化归思想,对此,教师可指导学生理解化归思想,巧妙将该思想应用于数学解题.例如在解答不等式问题时就可运用化归思想,提升解题能力.

在以上解题中,有效利用化归思想,将多个未知数用含同一个字母的代数式表示出来,对多元问题进行转化,通过等元抵消,快速计算得出结果.

总之,在初中数学解题教学中,教师可指导学生基于不同角度思考和分析问题,改变思维定势,灵活运用多种方式解决问题,提升解题效率,发展思维能力.教师指导学生运用多元解题技巧分析和解决问题,不仅能使学生学会应用所学知识与技能解决问题,而且能使学生对题目所涵盖的知识形成深刻印象,提升数学学习效率,更能帮助学生掌握多元解题技巧,拓宽解题思路,实现举一反三学习效果.