巧用数学思维 解答物理难题

吴宗德

(福建省连城县冠豸中学,福建 龙岩 366200)

在初中物理解题中经常应用的数学思维主要有:转化思维、逆向思维、方程思维、极限思维、数形结合思维[1].在物理教学实践中,教师若能运用好上述常用数学思维,结合教学进度,做好应用示范,将提高学生的解题能力,增强学生解题自信.

1 转化思维的应用

解答初中物理难题时若采用常规做法难度较大,过程较为繁琐,可考虑转化思维的应用,将看似复杂的过程进行合理等效,化繁为简,以达到高效解题的目的.转化思维对学生的思维能力要求较高,教学实践中为使学生能够跟上教学步伐,教师应预留空白时间,要求学生认真揣摩与反思,把握转化本质,使其真正理解与掌握,体会转化思维在解答物理难题中的应用,增强运用转化思维解题的意识.

“浮力”是初中物理的难点,对部分“浮力”问题而言采用常规方法作答,虽然能计算出最终答案,但是效率较低[2].教学实践中,教师可启发学生依据阿基米德原理进行转化,将物理问题转化为数学问题,借助数学中的“比例”知识,迅速得出结果.

例1 如图1,在水平面上放置一半径为2R圆柱形薄壁容器.将密度为ρ,高为h,半径为R的圆柱体木块竖直放置在容器中,随后向容器中注水.求使木块竖直漂浮时向容器中注入水的最少质量.

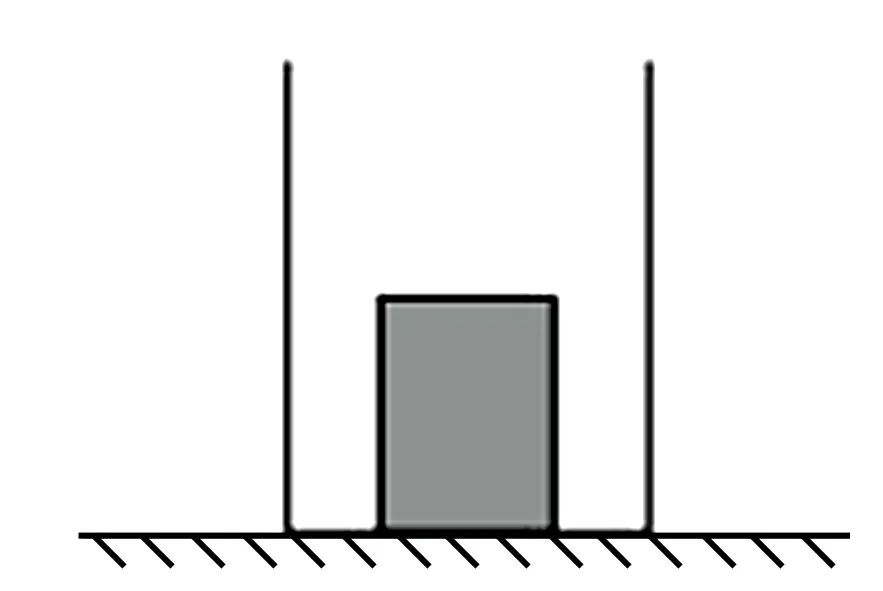
图1 木块置于容器中.

假设向容器中注入水的高度为h′时,木块刚好漂浮,此时其对容器底部的压力为零,木块受到的浮力和重力相等,由阿基米德原理可知木块排开水的重力刚好为其自身重力.m水g=ρR2πhg,对应该部分水的质量m水=ρR2πh.木块排开水的体积V排=R2πh′,将这部分体积看成水,则容器中可装入水的体积为V=(2R)2πh′,则V/V排=4.表明实际上容器中的水为3份,1份水的质量为m水=ρR2πh,则至少需加入水的质量为3m水=3ρR2πh.如此通过转化法解答该题,可减少复杂运算,提高解题效率.

2 逆向思维的应用

对于部分初中物理习题而言,大多数学生会想到正向思维,一步步地计算推理,效率并不高,而逆向思维则能节省不少时间.教学实践中,教师应讲解逆向思维并展示具体应用,认识应用逆向思维解题的必要性[3].

“电路故障的分析”是初中物理电学部分的热门问题.分析该类问题的方法灵活多变,对于选择题而言采用逆向思维,可迅速排除从而找到正确答案.

例2 如图2,将灯泡L1和灯泡L2串联(灯丝电阻保持不变)在电路中,其中L2的功率为4 W,且L1较L2亮,使用一段时间后L2灯突然熄灭,L1亮度增强,L1的功率为25 W,则L2出现的故障以及L2未熄灭之前,L1的电功率为( ).

图2 电路图

A.短路,1 W B.短路,9 W

C.短路,16 W D.断路,18 W

3 方程思维的应用

方程思维是求解未知参数的重要思维.根据经验,运用方程思维解答物理难题的关键点有两个:设出合理参数和根据物理定律构建等式关系[4].教学实践中,为使学生掌握运用方程思维解题的技巧,教师引导学生具备列出多个方程的意识,借助方程求解出目标参数.

“比热容”相关的计算是中考的重要考点.教学实践中,为提高学生解题的灵活性,掌握运用方程思维解题的具体思路,教师应驱使学生主动思考,确定方程参数,构建物理方程.

例3向盛有冷水的容器中倒入一杯热水,冷水温度升高10℃.继续倒入一杯同样质量和同样温度的热水,容器水温升高6℃.若此后连续向其中倒入5杯同样的热水,忽略热量损失,则容器水温会升高( ).

A.14℃ B.12℃ C.9℃ D.4℃

由题意可得倒入热水后,热水放出的热量和冷水吸收的热量相等,据此列出方程.

设热水质量为m0,冷水质量为m,开始时热冷水的温差为t.向冷水中倒入第一杯热水时:

cm0(t-10℃)=cm×10℃①;

倒入第二杯热水后,有:

cm0(t-10℃-6℃)=c(m+m0)×6℃②;

同理,连续倒入5杯热水,设容器水温升高Δt,有:

5cm0(t-10℃-6℃-Δt)=c(m+2m0)×Δt③;

联立①②得到:m=3m0,t=40℃.将这些数据代入到③解得Δt=12℃,选择B项.

4 极限思维的应用

极限思维又称极端思维,是向极端分析问题的一种思维.如将质量看作无穷大或无穷小就属于极限思维[5].

“杠杆”是初中物理中的重要知识点.对于部分“杠杆”类的问题,如采用常规做法,设出参数,列出方程,解题难度较大,而且也不一定得出正确结果.教学实践中,教师应引导学生尝试着使用极限思维分析问题,将看似复杂的问题直观化、简单化.

例4 如图3所示,将质量均匀等体积实心物体甲、乙分别挂在轻质杠杆的A、B两端,杠杆平衡.则( ).

图3 甲乙物体在杠杆中的情形

A.两物体切掉相等体积,杠杆右端下倾

B.两物体切掉相等体积,杠杆仍保持平衡

C.两物体切掉相等质量,杠杆左端下倾

D.两物体切掉相等质量,杠杆仍保持平衡

该题如设出参数列出方程,计算非常繁琐.为提高解题效率,解答该题应应用极限思维.因甲、乙体积相等,由图可知甲的质量小于乙的质量.切掉相等体积,甲、乙质量同比例减小,杠杆仍平衡.切掉等质量时,假设将甲的质量全部去掉,乙还剩余部分质量,杠杆右侧会下倾,综上分析选择B项.

5 数形结合思维的应用

运用数形结合思维分析问题主要分为两类:根据题干描述画出对应图形,借助图形将抽象、复杂的关系展现出来,更为高效地解题;从给出的图形中挖掘隐含条件,将图形与物理情境对应起来,寻找解题的蛛丝马迹[6].

“浮力”问题中,与图形相关的问题难度一般较大,需学生自己构建图形与物理情境之间的内在联系.教学实践中,教师应引导学生分析图线为什么是这个形状,拐点代表什么含义,帮助其找到解题切入点,运用数形结合思维解答物理难题.

例5 使用细绳将底面积为0.01 m2的长方体木块拴在空容器底部.而后向容器中缓慢加水,直到水和木块上表面持平.其中木块底部受到水的压强与注入水的深度图像如图4所示,忽略细线体积,g取10 N/kg,则( ).

图4 长方体在容器中的情境以及下表面所受压强和水深图像

A.细线的长度为7 cm

B.木块重力为15 N

C.细线对木块的最大拉力为6 N

D.木块的密度为0.6×103kg/m3

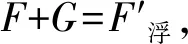
综上所述,在初中物理教学中,教师应将数学思维渗透至物理知识讲解中,尤其为提高学生的物理解题能力,应做好习题的筛选,逐一展示不同数学思维在初中物理解题中的应用,让学生真正理解并吃透不同数学思维在物理解题中的应用,促进其物理解题水平的进一步提升.