一种快速自动挖掘航空发动机工作模式的新方法
2023-07-29彭沛赵永平王雨玮
彭沛,赵永平,*,王雨玮
1.南京航空航天大学 能源与动力学院,南京 210016
2.北京航空工程技术研究中心,北京 100076
在大数据时代,航空发动机采集的传感器信息的应用由最初的事故原因调查扩展到发动机设计性能评估、飞行训练考核辅助评价、协助地勤人员进行状态监控及视情维护等方面。伴随着飞机整体性能的提升和发动机结构的复杂化,人们对飞行安全及发动机可靠性方面将会提出更高的要求,因而充分挖掘并利用飞行中发动机采集到的数据信息将会成为后续研究的必然趋势。传感器的测量过程由于发动机工作的复杂环境而易受随机噪声的影响,这就导致地面研究人员对原始获取的数据难以直观地分析研究。因此,如何将外场获取的数据最大程度还原出发动机在飞机飞行时真实的工作状态,这对后续基线模型的建立、实施状态监控及维护决策有重要的意义[1-4]。但研究人员处理发动机获取的传感器数据目前仍采用人工判读的方法,尤其在批量分析时会因判读数据量大而耗时耗力。另外,发动机环境参数的不同和个体制造的差异会导致判读规律的变化,这也增加了研究人员对工作模式判读的难度。
国内外为解决上述问题做出很多尝试。王奕惟等[5]将快速存储记录器(Quick Access Re‐coder,QAR)的数据图像化并采用卷积神经网络来判别状态。该方法本质上是对时间序列人为采样的单点识别而未考虑到传感器数据的动力学性质,这割裂了时序上的连续性,并且在识别过程中该方法也未考虑过渡态。CWT-CNN 方法[6]结合了小波变换和卷积神经网络,但其识别的单维时序样本并非含多种模式的信号,而是人为分割后单一模式的信号。此外,Cynthia 等[7]提出了将剪枝精确线性时间法[8]和自组织神经网络结合并给出过渡态的判别方法。该模型成功地识别了飞机的多个飞行状态,但仅涉及单维时序信号如油门杆角度,这样就忽视了真实数据中的时滞效应,即按油门杆角度切换模式时,其他监视参数如转速、瞬时耗量等不会同步地发生改变。
多维时序数据的挖掘在机械零件的传感器分析、金融财政等早有广泛的应用。此类问题可细分为时序分割、模式发现、模式匹配等任务。例如基于动态规划的算法[9]、剪枝精确线性时间法、基于模式的隐马尔可夫模型[10]、基于高斯假设的贪婪分割模型[11]。这几类方法仅能由不同模式来分割序列,并不能直接识别出模式,而且这些方法对参数调节很敏感,例如片段数和相关阈值等。在航空发动机收集到的大批量多维的时序数据下,不同航段采集的时序数据包含的工作模式数量和类别均不同,不同时序数据的要调节的参数有很大差别且随着数据量的增加调节参数往往会耗费大量的时间。在这种场景下理想的方法应该能寻找任意的模式并不受参数的影响,即无参数化。AutoPlait[12]是基于多级链隐马尔可夫模型,它利用无损压缩原则实现模型无参数化。Auto-Cyclone[13]也采用相似的思路实现模式季节性挖掘。但上述2 种方法并不适合于发动机的工作状态的挖掘,它们更倾向于挖掘有季节性的模式而模糊了发动机的稳态模式和过渡态模式的界限,并且复杂的过渡态模式也无法给出很好的处理方法。事实上,上述2 种无参数方法更适合于飞行动作识别,但模型训练也需要丰富的飞行姿态数据。
考虑到现有方法在实际工程中遇到的诸多问题,本文针对航空发动机工作时产生的时序数据,设计了一个快速自动挖掘工作模式的方法,即AutoMiner。该方法自然地集成了时序分割、模式发现和模式识别任务,它以最原始的全航段多维时序数据为研究对象,采用最小编码代价的原则进行模型无参数化,以应对多变的时序数据。并且该方法还借鉴了标记传播的思想[14]来解决过渡态的识别问题。在模型训练方面,该方法支持并行化并利用储存单元省去多次重复计算,这大大缩短了训练时间。本文模型的设计初衷为航空发动机工作模式的挖掘,但由于模型的可迁移性,还能被应用于更高级模式的识别,如飞行动作。最后,在准确度、迭代效率、可迁移性等方面,本文开展一系列实验,通过与多种方法对比可视化地展示了AutoMiner 方法的优越性。
1 AutoMiner 方法优化目标
该节介绍工作模式的线性模型,由最小化编码损失的方式提出优化目标,并给出利用标记传播法识别过渡态在内的发动机工作模式的方法。
1.1 工作模式的线性模型
从航空发动机上获取指定的传感器数据,可组成多维时间序列X=[x1,x2,…,xn],xi为第i时刻的d维列向量。假设模型根据X的本征模式能将其分割成K段,即S={s1,s2,…,sK},第i段si可视为X中由断点τi和τi+1分割的部分,则断点序号集组成τ={τ1,τ2,…,τK+1},其中τ1=1,τK+1=n。S中每段按照工作模式可以赋予相应标记并组成F={f1,f2,…,fK},fi∈{1,2,…,c}表示第i段si属于工作模式fi,c为工作模式总数。
当航空发动机处于相同工作模式时,内在物理规律应是相似的,工作模式的转变会引起这种内在物理规律的变化,而这种规律体现到可测传感器数据上就是多维时序数据的变化。由此思路,对S中每个片段建立数学模型,自然地认为相同工作模式的数学模型是相似的,而不同工作模式的模型会有显著区别。对第i段si可建模为
1.2 总编码代价的计算
在计算过程中,编码描述数据X及储存算法模型需要付出一定的代价,而最小编码代价对应的模型是最理想的,这个思想与经典的奥卡姆剃刀定律相似。于是,可建立优化目标为
式中:CT表示编码的总代价,即本文所需最小化的优化目标,分别由描述算法模型的编码代价和算法模型应用到数据X后产生的编码代价组成。
假设本文讨论的编码过程均是无损的,定义符号log*(a) 为对整数a的编码长度[15],即log*(a)=log2(a)+log2(log2(a))+…,按此规律求和且只有正数项包含在求和项中。AutoMiner算法模型简式为:{Θ1,Θ2,…,ΘK,S,F,K,r},r代表S中片段的总类别数,区别于1.1 节中提及的工作模式数c。例如本文涉及到8 个稳态模式,则包含过渡态后总的模式数c为9,在优化目标中总类别数r的计算方法为
式中:IF(⋅)为判断函数,例如对IF(l∈F)而言,若语句l∈F为真,则取值1,反之为0。式(3)中r将前8 个稳态按是否出现计算,第9 个表示的过渡态按出现次数计算。
式中:cF为浮点系数[16],其默认取值为4×8,即32 bit;q为线性模型的阶数。
由①~⑤便可获得算法模型编码所需的代价,即式(2)第1 项,而式(2)求和中的第2 项,体现模型在给定数据X完成任务的能力,即序列分割及模式挖掘的准确度。本文采用哈夫曼编码,将编码代价转化为线性模型的似然概率,得到
式中:Θ={Θ1,Θ2,…,ΘK};P(X|Θ) 为似然函数值。
考虑到同一工作模式中线性模型的相关参数应尽可能相似,利用式(1)中偏差项服从正态分布的性质,构造对数似然函数为
式中:det 表示对矩阵取行列式;l(i)表示由第i个片段计算得到的对数似然函数。
在序列分割过程中,当片段长度|si|小于维数d时会导致矩阵求逆出现病态,本文引入正则化的方法将式(6)进行改造,如式(7)所示,这种正则化方法常用于解决高维时间序列的问题[17]。
式中:λ为正则化系数,常取较小值,本文取10−5;tr 表示矩阵的求迹运算。
通过极大化对数似然函数能求解出参数Θ,令式(7)对Θ的偏导数分别为0,得
式中:Ιd表示d阶单位矩阵。当不考虑正则化时即λ=0,Σi与相等。式(7)求偏导数涉及到诸多矩阵运算,对式(8)更详细的推导可见附录A。
于是,将式(8)结果重新代入式(7),可得到最大似然值的结果,并结合式(5)和式(6)可得
综合式(5)、式(9)可得式(2)第2 项的表达式为
式中:为便于后续对编码代价迭代求解断点,将结果化为ϕ(τi,τi+1)的求和,且该项只与断点有关。
最后可以通过①~④及式(4)、式(10)获得编码的总代价CT,即模型的优化目标
式中:优化目标仅为断点集τ的函数,随后便可寻优出合适的断点组合,并使总编码代价最小。
1.3 基于标记传播的含过渡态时序挖掘方法
在计算式(11)中编码的总代价CT前,还需在寻优迭代过程中对片段集S赋予合适的标记集F,即找到每段隶属的工作模式。在计算出F后便可由式(3)计算出总类别数r。
根据本文含过渡态模式的工程场景可做出如下描述:在F标记集中,第i段si可以划分为模式fi∈{1,2,…,9},其中前8 个模式为稳定态,第9 个模式为过渡态。假设已获得待识别片段序列为s0,对该段序列建立线性模型可获得参数Θ0并组成样本点。参照行业工程手册以及专家建议可按同样方式选取特征生成带标记的参照样本集表示采集第i个参照片段数据后维的特征向量,实验中为Θ0包含的参数总数。记参照样本集的对应标记矩阵为YL=[y1,y2,…,ym],9 维的标记向量yi中除第l个元素yil为1,其他项均为0,即表示参照数据属于第l类模式。由于可获取的参照样本仅为前8类的稳态模式,则参考样本的标记中yi9均为0。
式中:迭代过程中的初始标记值Y(0)被赋值为先验标记矩阵Y,其值被预先人为设置。式(13)中第2 项表示先验信息在传播时的参与程度。为让传播过程中仅改变标记y0,比例矩阵Dα设置为分块矩阵,α越大即待标记数据会接收更多其他点的信息,本文默认取值为0.99[18]。
不难证明式(13)的迭代必收敛于式(14)。
由式(14)获得软标记y0,其每个元素表示样本隶属对应模式的概率,选取最大概率对应的序号l即为所属的模式。本质上,参照样本集虽只含稳态模式,但该方法利用标记传播更新生成了软标记,使得过渡态模式对应的软标记值在这里充当着剩余概率的角色,即样本不属于前8 种稳态模式的概率。
时序模式识别步骤如算法1 所示。为尽可能降低计算复杂度,在采用式(13)计算W时对已知的距离矩阵无需重复计算。于是由算法1 步骤2 可将算法1 的计算复杂度由O(m2)降至O(m)。

算法1 工作模式时序挖掘算法Algorithm 1 Working mode time-series mining algorithm
2 断点寻优的启发式算法
式(12)得到总编码代价仅与断点τ有关,问题转化为寻找最优的断点组合使总编码代价最小,在该断点组合下对应的片段集S以及标记集F即是AutoMiner 方法挖掘时序数据X获得的最优方案。在AutoMiner 方法中提出的断点优化算法是种启发式算法,它无需全局遍历所有的解而是在迭代范围内找寻局部最优的组合。每一次迭代时添加一个断点,并局部调整断点组合以保证总编码代价总是维持着最小值的状态,直到找到总编码代价不再减小的断点组合。这个思路类似标准的“自上而下”方法[19],但该方法容易陷入局部最优并且承担着较高的计算成本。本文将提出的启发式算法细分为图1 所示的3 个步骤来分别介绍。
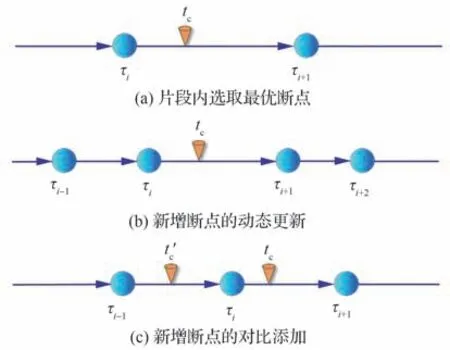
图1 断点寻优示意图Fig.1 Schematic diagram of breakpoint optimization
2.1 时序片段内最优断点选择策略
启发式方法如图1(a)所示。从式(12)中可以看出,每次迭代添加的断点仅对断点所在的片段产生影响。于是做出下述约定:对于片段si而言,在其内添加的一个断点t并将片段si分别分割为左右2 个子片段,其总编码代价的变化量为
式中:g是K0、r0、K1和r1的函数,它由式(4)和式(11)计算获得。式(10)中展示了与断点有关的函数ϕ的表达式。K0和r0为添加断点t前的总断点数和总类别数,同理添加断点后可表示为K1和r1。易知K1=K0+1,而r0和r1可由式(3)获得。
在si内寻找最优断点tc的思路如算法2 所示,其中算法中总断点数K、添加断点前的标记集F等均默认已知。算法2 步骤1 表示从τi+T到τi+1−T以寻优步长T来迭代选取t,设置较低步长有利于精确的搜索但会增加计算时间。
此外,算法2 还采取了其他减少计算开销的方法。由于对于算法2 步骤1~步骤7 的循环之间并未存在联系,即可支持并行化计算来节省大量计算时间。引入储存单元Pi是为了将此次寻优结果保存下来,防止后续迭代过程循环调用算法2。而选择总代价的变化量作为判断指标,也从一定程度上,避免了直接比较总编码代价带来的计算高额量。若考虑并行化,算法2 对于si的计算复杂度可由降为O(md2)。

算法2 时序片段内部最优断点选择策略Algorithm 2 Internal optimal breakpoint selection strategy for time-series segments
2.2 断点的动态更新策略
由于寻优算法的策略是启发式的,为了最大程度避免陷入局部最优解,在每次迭代添加断点后需要动态回顾全局,再次更新断点组合以保证求解的断点组合的总编码代价保持最低值。参考图1(b),更新策略如算法3 所示。当K不大时更新次数将是适度的,而随着K的增大,每次更新只影响局部断点且多次迭代后断点集趋于最优组合,所以在容错阈值范围ξ内更新一定会在适度次数后收敛,实验中ξ=5。在算法3 步骤2中,栈储存添加点或变化点,随后每次仅对栈弹出点的邻域最近两断点进行更新。在断点改变后也会同步更新原来的片段,这时与片段对应储存单元中的内容将会清除并等待下次调用算法2 时再次赋值。

算法3 添加断点后的动态更新策略Algorithm 3 Dynamic update strategy after addition of breakpoints
2.3 断点的寻优算法
依照图1(c),算法4 中展示了寻优的总体思路。算法4 中步骤3~步骤12 的循环是独立运行的并支持并行化运算。在算法4 步骤2~步骤27中,若片段si未因断点更新改变且该时序片段的最优断点未被此次迭代选中,下一次迭代开始时便无需对si重复寻优,这也是设置存储单元Pi的目的,因此每个存储单元总是唯一地指向片段si。若断点平均更新次数为L,算法3 的计算复杂度为,K为求解获得的最优断点数。考虑并行化后,计算复杂度为。

算法4 断点寻优的启发式算法Algorithm 4 Breakpoint-seeking heuristic algorithm
在某航段上截取部分简单的三维时间序列并可视化地展示AutoMiner 方法断点寻优的工作流程图,如图2 所示,其中M2 为过渡态模式,而M1、M3、M4对应不同的稳态模式。算法初始目标是添加单个合适的断点使得总代价下降,这仅需对时序数据扫描一次便可得图2(a)。随后,图2(b)~图2(d)为逐步添加断点的过程。由于算法4步骤22 加入了终止条件,算法将在第6 次迭代时终止并将第5 次的迭代结果作为最优断点组合输出。如图2(e)所示,若不加以约束添加断点总代价反而会随之增加。
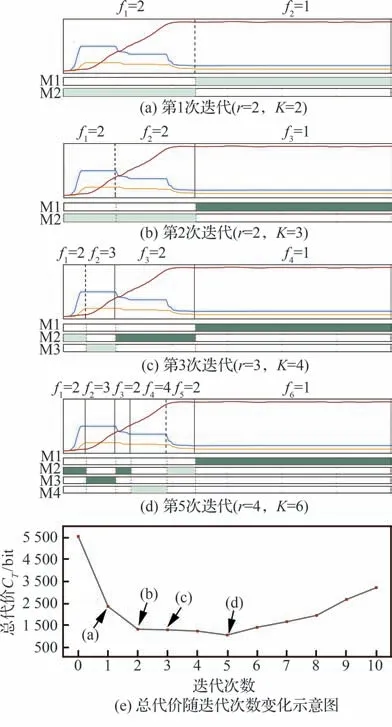
图2 AutoMiner 方法寻优流程Fig.2 Optimization process of AutoMiner method
3 实验分析
图3 是将AutoMiner 方法运用于实际工程场景中的示意图。可以看出该方法将从外场采集发动机上原始的传感器数据进行自动处理以获得大批量数据能进行后续的分析。参考样本集按研究的时序对象而变化,常可通过专家研究设计手册或借鉴历史已标注工作模式的数据来获得。此处历史数据中包含了不同退化状态下的工作模式数据信息,但实际中退化量与出厂的理论值通常偏差不大,选择手册的信息作为参照也是合理的。
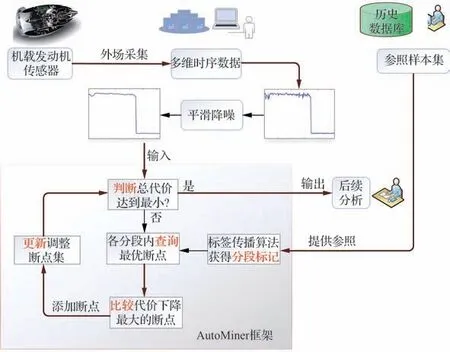
图3 实际工程场景应用的示意图Fig.3 Application diagram of engineering scenario
3.1 实验背景
本文以某型机载航空发动机在飞行过程中采集的多组传感器数据为研究对象,实验中涉及3 组飞机全航段工作数据,此处一个航段记录为飞机的一次长时间飞行任务。这些数据囊括了实验考虑的全部工作模式,在飞机飞行时由4 台同型号发动机的传感器进行同步测量。
对于实验参数的筛选需要参考实验手册,选取随工作模式的变化量最大的多个物理指标,比如绝对气压高度体现了飞机起飞降落及巡航状态,从而也反映发动机工作模式的变化。在工作模式需要改变时,飞行员会通过外部干预调节油门杆角度,这会引起发动机转子转速、瞬时耗量等物理量的变化。为解决参数的时滞效应,本文选择上述4 类物理指标作为不同工作模式的分辨依据,其中油门杆角度、转速和瞬时耗量均由2 组以上传感器参与测量,收集以上数据可共同组成描述发动机工作状态的多维时间序列。后续实验将证明,考虑发动机传感器的多维时序数据比常规只考虑单组油门杆角度作为辨别依据的方案更能适应复杂的数据情况。本文涉及的发动机工作模式的人为编号如表1所示。

表1 某型航空发动机工作模式说明Table 1 Description of operating mode of aero-engine
3.2 数据预处理
飞机常需要应对复杂的飞行条件甚至完成某些高难度的动作,这使得发动机上测量的参数不可避免地会产生波动,并且热力及电磁环境干扰和不稳定的传感器测量状态也会引入噪声。为了减少噪声以提高挖掘时序数据信息的准确度,便需要对采集到的数据进行平滑降噪。选取某航段上一台发动机的油门杆角度进行比较,实验方法包括滑动中值滤波[20]、滑动均值滤波以及小波软阈值滤波[21]。对比实验结果如图4 所示。数据点之间采样间隔为1 s,考虑到滤波时尽可能保留过渡态模式信息,选择滑动窗口的长度为60 s,同时采用8 层小波分解来计算近似系数。
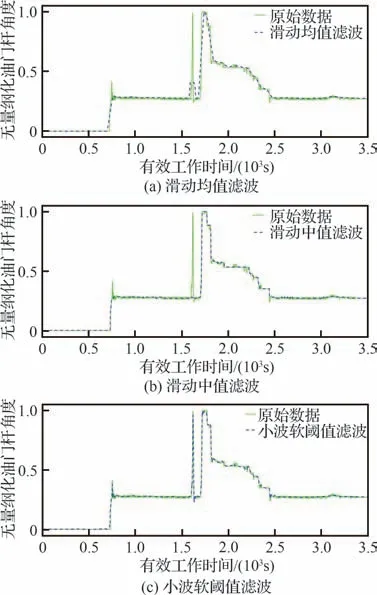
图4 3 种滤波方法的对比结果Fig.4 Comparative results of three filtering methods
由于中位数面对异常数据以及高频噪声更加鲁棒,从图4 中可以看出相比均值滤波而言,中值滤波能得到更适合识别工作模式的时序数据。在小波软阈值滤波中,不同分解的层数及合适的小波基会随着时序信号的改变而变化,因此不适用于大批量自动处理数据的场景。
3.3 具体工程场景下的算法实验
为展示AutoMiner 方法在航空发动机工作模式挖掘场景下的优越性,本节提取部分航段中传感器采集的时序数据与多种时序分割算法对比,包括基于高斯核的KCP 方法[22]和基于高斯模型的GSS 方法[11]。为在模式挖掘和无参数化算法方面进一步比较,对比算法中还包括成功运用于飞行模式挖掘的PELT-SOM 算法[7],以及基于多级链隐马尔可夫模型的AutoPlait无参数化算法[9]。
3.3.1 时序分割能力的对比评估
在时序分割方面,合适的评价指标至今仍是广泛讨论的内容。例如,专家评判分割断点在第1 000 s,模型求解出断点为第1 005 s 是否有效。若容错阈值为10,模型得到的断点为第1 011 s是否应该被惩罚。严格的惩罚制度得到准确度、混淆矩阵等指标并不适合时序分割问题[23]。上述问题归结于对评判边界并未做出合适的处理,本文借鉴文献[24]的思路选择评价指标为R分数,其表达式为
式中:τ(1)为模型求解的断点集。数据真实的断点集τ(2)中距离断点最近的断点表示为,此处讨论不包含时序数据的起点和终点。指标R的取值范围为0~1,其值越大说明该模型分割效果越好。
采集部分飞行航段上发动机传感器数据进行了2 组实验,实验中各物理量仅展示1 个传感器的测量结果并通过一定比例地无量纲化操作绘制出如图5、图6 所示的曲线,其中曲线图中的分割线为人工结合工程经验给出,即可视为真实的分割断点位置。另外,图5(b)、图5(c)、图5(f)和图6(b)、图6(c)、图6(f)涉及算法均可支持工作模式的识别,而图5(d)、图5(e)和图6(d)、图6(e)中仅支持对时序数据的分割,其中对比算法中参数β为惩罚系数,λ为正则化系数,M 表示某些对比算法对该工程场景失效而仅识别出的未知模式。

图5 在航段1 中工作模式挖掘的可视化图Fig.5 Visualization of pattern mining in Flight segment 1

图6 在航段2 中工作模式挖掘的可视化图Fig.6 Visualization of pattern mining in Flight segment 2
将时序分割结果代入式(16)中可得到表2。理想的算法应该具有较高的R分数且生成断点数接近于真实断点数。由于图5、图6 中可以看出航段2 相比航段1 包含更丰富的工作模式,在复杂的数据组成表2 中航段2 的R分数也会相较航段1 偏低。对于PELT-SOM 和KCP 算法而言,惩罚系数越小,意味着允许生成更多的断点,一方面会使R分数在一定程度上增大,但过多的断点会增加计算时长,同时使模型结果过于复杂而不利于后续分析。从图5(c)和图6(c)中可以看出,若惩罚系数过小,算法会忽视某些必要的过渡模式。就GSS 算法而言,相比上述2 种算法表现相对更好,但其不支持模式挖掘功能并且需要提前调节超参数,它并不是此场景下最好的选择。由于AutoPlait 算法设计初衷为捕捉更高级复杂的模式,且并不能适应过渡态和数据的无规律变化,这导致该算法在2 个航段上的实验并不理想。综合表2 和图5、图6 不难看出,AutoMiner 方法在航段1 和航段2 上较其他几类方法表现更优越。
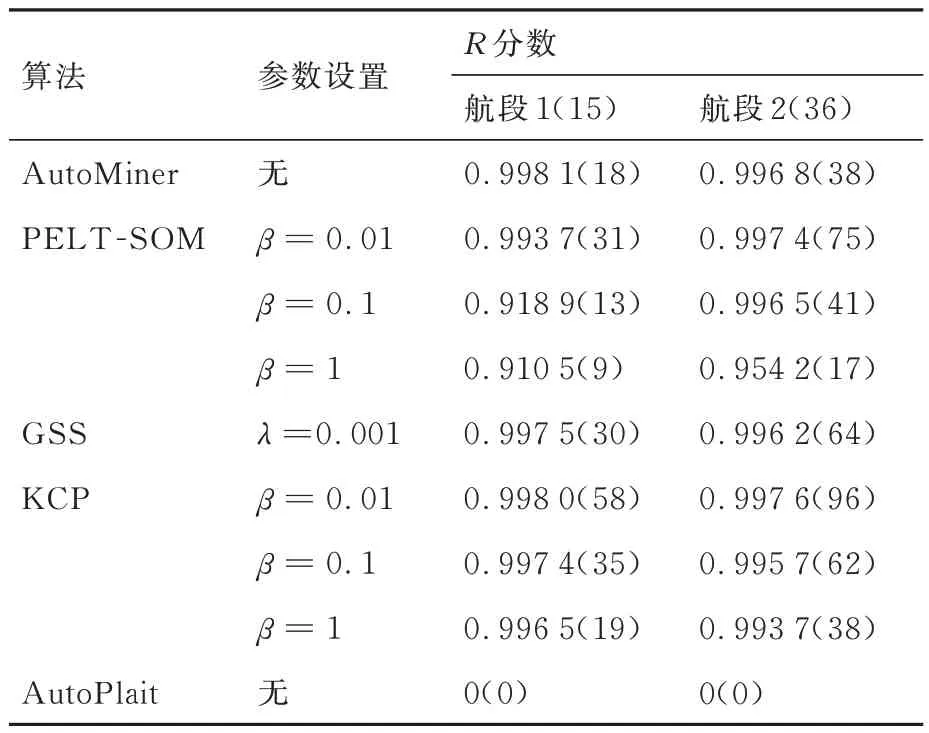
表2 在航段1 和航段2 上分割评价指标R 分数的对比Table 2 Comparison of split evaluation indicators R score on Flight segments 1 and 2
3.3.2 算法可迁移性的实验解释
为研究AutoMiner 算法在更高级模式的挖掘能力,随机选择有规律性的时序数据,改变模型阶数可获得图7 中的结果。由航段3 的实验可以看出,复杂的模型可以挖掘出由多个工作模式组成的更高级的模式。图7(c)、图7(d)中斜线块所示为高级的模式,由于未提供相应高级模式的参照数据集,其自然地被视为过渡态模式。模型阶次越高意味着算法采用了更复杂的模型,这可以挖掘出更复杂的模型状态。如图7(e)的算法中选择多级链马尔可夫模型便可以挖掘出图中M1~M5 所示的更高级的工作模式。

图7 在航段3 中算法迁移性实验Fig.7 Algorithm transportability experiments in Flight segment 3
3.3.3 实验迭代过程的讨论
在未采用并行化措施时,AutoMiner 算法计算复杂度为。从航段2 的实验可以看出,随着迭代次数的增加,每步迭代需要的时间将快速减少,这是因为随着断点的增多对应时序片段长度较少,加上引入存储单元也大大缩短了后续迭代所需的计算时间。图8 中T为采样步长,图例中括号为与之对应的评价指标R分数。从图8 中可以看出适当增大采样步长会使算法总耗时急剧减少,但在一定程度内分割指标的减少量并不大,所以可以根据实际情况适当增加采样步长牺牲较少的精度以换取较低计算成本。
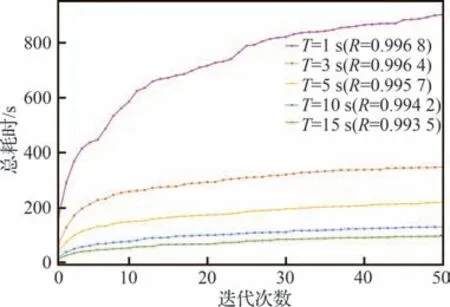
图8 航段2 中算法总耗时随迭代次数的变化Fig.8 Variation of total time consumed by algorithm with number of iterations in Flight segment 2
图9 为AutoMiner 算法在航段1~航段3 上求解断点组合时总代价随迭代次数的变化图,其中选用的模型默认为一阶线性模式。为获得完整的总代价趋势变化图,将算法4 步骤22 的中止功能暂时关闭。在图9 中变化曲线存在明显的拐点,在迭代达到曲线极小值点后,进一步增加断点数量反而会使总代价增大。另外,通过式(10)的分析不难发现,当模型和时序数据间的模型误差逐渐减小,即足够小时,编码代价会在数值上变为负数,但这与总代价最小化的寻优策略并不矛盾。
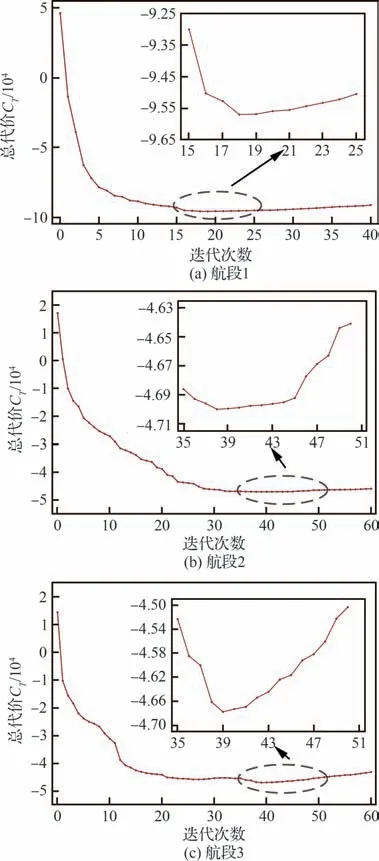
图9 AutoMiner 算法在迭代过程中总代价的变化Fig.9 Variation of total cost of AutoMiner algorithm during iteration process
3.3.4 模式挖掘效果的对比评估
现今模式挖掘效果的评估方法常采用准确度、F1分数,其中F1分数是由混淆矩阵得到的精确率和召回率的调和平均数。在航段1~航段3来源更完整的3 组航段上继续开展实验,将Au‐toMiner 算法挖掘的工作模式与PELT-SOM 算法的结果进行比较可以得到表3 所示结果。从中可以看出过渡态模式上2 种方法的各项指标均弱于稳态模式,而相较之下AutoMiner 方法会获得更好的结果。若时序数据位于2 种工作模式之间,例如图5 中前1 000 s 对应发动机停转,PELT-SOM 会将其与最相似的稳态模式即慢车模式优先匹配从而导致判断失误。AutoMiner 方法通过标记传播获得软标记,比较属于各模式的概率并把不属于稳态模式的概率视为过渡态从而解决了此类问题。

表3 模式挖掘评价指标的对比Table 3 Comparison of evaluation metrics for pattern mining
为了对模型获取时序片段的工作模式开展可视化分析,选用t-SNE 方法[25]将从原始时间序列中提取的多维特征降至二维的特征图上并绘制如图10 所示散点图,图中按模式总量排布并且括号中表示通过不同模型挖掘出的对应工作模式的时序片段数量。图10(b)中软标记最大值代表对应工作模式的概率值,它在图10(b)中表示为散点的形状大小。由图10 可以看出AutoMiner 模型获得的工作模式更加接近于真实的工作模式。
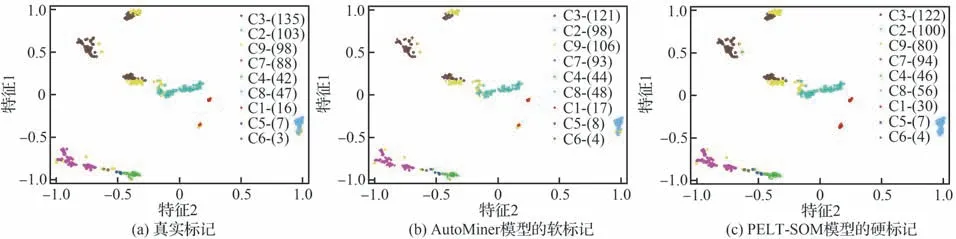
图10 所有时序片段的工作模式的可视化分布Fig.10 Visualization of pattern distribution of whole time-series segmentation
4 结论
1)AutoMiner 方法通过对模型进行编码,利用编码代价最小的思想来获取最优的时序片段组合,并在分段时利用标记传播来解决过渡态模式识别的问题。相较单变量的方法,本文采用的多变量方法能更好地解决状态参数的时滞问题。
2)通过在某型发动机全航段数据上的实验表明,在与诸多算法对比后,AutoMiner 方法在分割指标以及模式挖掘指标上均表现优异。
3)AutoMiner 方法支持并行化计算并采取诸多措施加速迭代过程,实验还证明了该方法在更复杂工作模式方面具有很好的可迁移性。
附录A:
1)式(7)对θi求偏导数并令之为0,求解θi。
求解对θi的偏导数时,将Σi视为已知常数矩阵,并对式(7)的迹取微分可得:
依照微分和偏导数转化公式并结合迹的性质可将式(A1)化为
对式(A2)化简后得到
令式(A2)为0,即可化简出式(8)中θi的结果。
2)式(7)对Σi求偏导数并令之为0,求解Σi。
同样,求解对Σi的偏导数时,将θi视为已知常数矩阵,并对式(7)的迹取微分可得:
式(A4)可化为含A矩阵的形式,可以直观看出A矩阵为对称矩阵,便得到所求偏导数如式(A5)所示,A矩阵在此情形下可以视为雅可比矩阵。
式中:Id为d阶单位矩阵;符号“∘”表示矩阵的哈达玛积,即矩阵点乘。若矩阵A由元素aij组成,令式(A5)结果为0,可得
式(A6)反映出A=0,化简可得式(8)中Σi的结果。
