双面柱声学超材料在汽车前围板上的应用

鲍瑞雪

（山东理工大学 交通与车辆工程学院，山东 淄博）

汽车内的振动和噪声水平不仅影响乘员的舒适性和对路况的判断能力，还可能使传感器等精密仪器的性能、精度降低，甚至失效。声学超材料能带理论的研究为解决这一问题提出了一种新的方法：将超材料按照特定的人工周期结构排布在工程结构（如板、梁等），利用带隙特性抑制结构中波的传播，以降低振动。带隙特性赋予了超材料特定频率范围内几乎完全吸收振动和噪声的能力，这是传统复合型隔声和吸声材料所不具备的。近期的研究工作表明，通过超材料单胞结构的合理设计，可在低频段获得带隙。

Shen 等人研制出一种“三明治”声子超导材料[1]，并在此基础上得到了兰姆波的低频带隙。格栅结构是一种形如网状的结构，因其质量轻、结构稳定性好、材料耐磨性强等特点，在航空航天领域具有广泛应用前景。苏开创[2]设计的单面柱声学超材料采用了多相材料，用长方体取代圆柱体作为单面柱结构声学超材料散射体形状，提高了声学超材料的低频带隙性，提高了减振性能。Wang Peng 等研究了单相材料（铝）做成的双面柱板材料[3]，采用了有限元法这样的单相结构也具有弹性波带隙产生，而且研究了板柱两侧对称性与声学超材料带隙性质变化的关系，指出越是完美对称柱体的双面柱声学超材料带隙性质越好。

本文基于已有研究，利用声学超材料的相关理论知识和能带结构计算方法，设计双面柱型声学超材料单胞结构并建立有限元模型，进而开展有限周期排列的声学超结构减振性能分析，对汽车前围板的隔振应用进行研究。

1 双面柱声学超材料的设计

如图1 所示为设计的双面柱声学超材料的有限元模型。单胞由基体板和柱体组成，本文设计采用多相材料构建双面柱声学超材料，即基体板和柱体为不同材料。

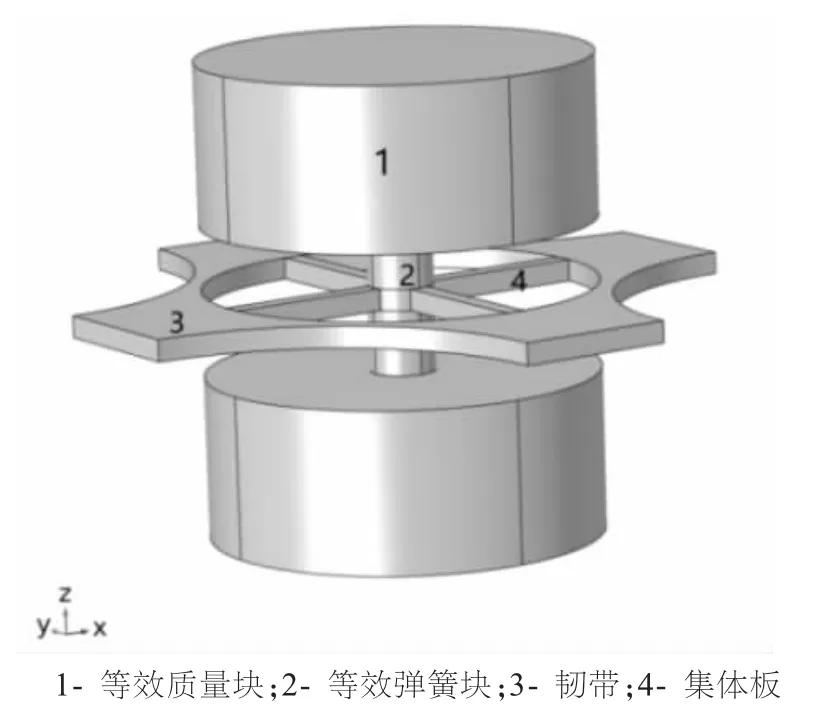
图1 双面柱声学超材料单胞模型

单胞的几何参数为：晶格常数L=10 mm，图1 中1号部分等效质量块参数：等效质量块的半径R1=3 mm，等效质量块的高度H1=2.5 mm。图1 中2 号部分等效弹簧块参数：等效弹簧块的半径R2=1 mm，等效弹簧块的高度H2=1 mm。图1 中3 号部分韧带参数，韧带宽度W=0.3 mm。图1 中4 号部分基体板参数：基体板的孔外半径R3=3 mm、基体板的孔内半径R4=0.5 mm基体板穿孔半径R5=3.8 mm、基体板的板厚H=L/30。单胞的材料参数为:钢材的参数：密度为7 850 kg/m3、杨氏模量为200 e9Pa、泊松比为0.3；有机玻璃的参数：密度为1 180 kg/m3、杨氏模量为3 e9Pa、泊松比为0.3。

利用Comsol Multiphysics 多物理场仿真软件，对声学超材料的能带结构进行了数值模拟：

通过分析图2，本次设计的双面柱声学超材料模型的第一带隙的下截止频率为950 Hz，上截止频率为1 400 Hz，带隙频段为950 Hz-1 400 Hz，带度为450 Hz。该模型符合预期的设计目标，带隙下截止频率：1 000 Hz，带宽：≥200 Hz。

图2 双面柱声学超材料模型的能带结构

2 有限周期双面柱声学超材料的减振性能分析

根据上述双面柱声学超材料单胞模型从而进行周期排列，y 轴方向单胞数量为5 个，x 轴方向周期为无限。建立双面柱声学超材料有限元模型如图3。

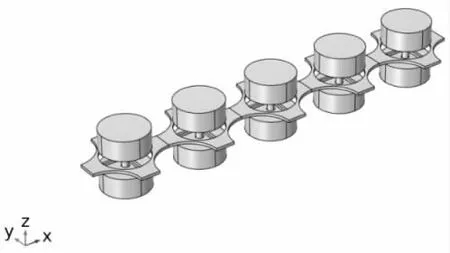
图3 双面柱声学超材料有限周期模型

由上述模型，利用Comsol 仿真模拟软件对该模型进行仿真模拟，采用固体力学模块，对单胞周期性排列。在结构的左端面施加一定频段的简谐位移载荷，设置变量函数和传递率公式，分别选择图3 第一个单胞左端面和第五个单胞的右端面作为输入端和输出端测试的积分边界。进行仿真模拟研究，得到双面柱声学超材料周期性排列结构的弯曲波的传输响应。

仿真结果：在频率500 Hz-1 500 Hz 时，周期结构的弯曲波传递率为负数，即弹性波在该频段内无法有效传输，与第一节中的带隙频段（1 000 Hz-1 400 Hz）不一致。超材料的色散关系x 方向传输光谱图如图4，共振模态的位移表现为沿x 方向为反对称的位移场分布，符合盲带的性质。如图4 所示，500 Hz-800 Hz即为盲带，除去盲带的部分为900 Hz-1 500 Hz，与第一节的带隙频段相符合。因此，本文设计的双面柱声学超材料不仅符合要求，并且具有更宽的波衰减频率，可以达到预期设计目标，也验证了本文设计的双面柱声学超材料的优良减振性能。

图4 双面柱声学振应用

3 汽车前围板的隔振应用

利用已有研究，选取本文设计所需要的汽车前围板3D 有限元模型，转化为stl 文件形式，再将转化好的汽车前围板stl 文件导入到Comsol 仿真模拟软件中，建立出汽车前围板有限元模型。将第二节优化好的单胞模型放入前围板模型中。建立周期为不规则排列、密集覆盖的单胞，保证单胞覆盖率在70%左右。

为了方便计算，通过类比的方法简化双面柱声学超材料导入前围板模型部分，建立汽车前围板有限元模型。通过截取汽车前围板模型平整的一小部分，建立一块平板，进行类比替代整块汽车前围板模型。再将单胞按照密集覆盖、无规则排列的方式排列到建立好的平板上，如图5 所示。

图5 类比简化的汽车前围板有限元模型

建立的类比简化的汽车前围板有限元模型的尺寸为长度为100 mm，高度为150 mm，材料为钢，放置的单胞数量为7 个。为了方便计算，再次进行类比简化，用壳- 梁单元进行汽车前围板有限元模型的建模，并完成弯曲波传递率的计算。通过等效的方式，将双面柱声学超材料单胞模型的基体板等效成一块壳结构，将双面柱声学超材料单胞模型的柱体等效类比成梁结构。具体等效的效果如图6 所示。

图6 等效的壳- 梁结构单胞

将双面柱声学超材料单胞模型等效成壳- 梁结构，壳单元厚度为0.4 mm，两个梁结构截面为半径3 mm 的圆。对壳- 梁结构单胞进行带隙频段仿真模拟，验证壳- 梁结构单胞类比代替之单胞结构的正确性。壳- 梁结构单胞模型的模拟带隙图如图7 所示。

图7 类比简化的壳- 梁结构单胞的能带结构

从图7 中可以看出，壳- 梁结构单胞模型的带隙下截止频率约为900 Hz，带隙上截止频率约为1 300 Hz，模型的带隙频段约为900 Hz-1 000 Hz，符合设计目标。验证了壳- 梁机构类比简化单胞的正确性。

将壳- 梁结构单胞模型通过有限周期排列，组成壳- 梁结构有限周期模型，x 轴方向单胞数量为5 个，y 轴为无限周期，与第2 节建立的双面柱有限周期模型类比简化，具体效果如图8 所示。

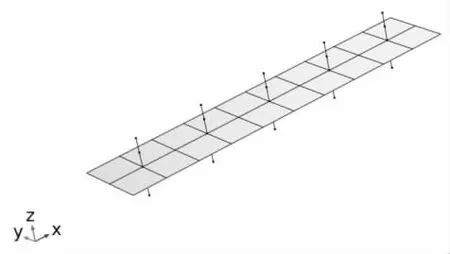
图8 壳- 梁结构有限周期模型

通过壳单元建立双面柱声学超材料有限周期模型，得到壳- 梁结构有限周期模型。再对得到的壳-梁结构有限周期模型进行弯曲波输入输出仿真模拟，得到弯曲波的传递率，结果如图9 所示。

图9 壳- 梁结构有限周期模型弯曲波传递率曲线

由图9 得出，壳- 梁结构有限周期模型在大约1 000 Hz-1 800 Hz 弯曲波传递率小于0，符合壳- 梁单胞模型带隙频段，证明壳- 梁结构有限元模型的有效的减振性，也验证了壳- 梁结构有周期模型的正确性。

将建立好的壳- 梁结构有限元单胞放入一块平板中，类比简化双面柱声学超材料单胞排列在汽车前围板有限元模型，得到壳- 梁结构汽车前围板有限元模型。

将壳- 梁结构汽车前围板有限元模型进行弯曲波输入输出仿真模拟，获得壳- 梁结构汽车前围板有限元模型的弯曲波传递率，结果如图10 所示。

图10 壳- 梁结构汽车前围板有限元模型的弯曲波传递率

由图10 可以得知，在频段大约为800 Hz-1 500 Hz时，壳- 梁结构汽车前围板有限元模型的弯曲波传递率小于0，与前面单胞的带隙频段相符合。证明了壳-梁结构有限元模型的有效减振性，也验证了壳- 梁结构汽车前围板模型的正确性。

4 结论

本文提出的双面柱声学超材料在汽车前围板上的应用，有助于推进车辆振动噪声控制技术的发展。主要得到以下结论：

壳- 梁结构的单胞模型的能带结构图的带隙上截止频率和上截止频率以及带宽均符合设计目标，壳- 梁结构有限周期的弯曲响应图的波衰弱频段符合单胞带隙频段，证明了壳- 梁结构的正确性。壳- 梁结构汽车前围板的弯曲波响应证明双面柱声学超材料应用在汽车前围板上壳以有效减振。