基于学生测评数据的试卷讲评改革

陈冰心

20世纪90年代以来，我国的信息化教育建设经历了4个阶段：教育信息化萌芽期（1978—1999年）、教育信息化建设驱动发展期（2000—2010年）、教育信息化应用驱动发展期（2011—2017年）、教育信息化2.0新时期（2018年至今）。教育信息化数据化对提升教学效果有较大的帮助，可以使教师对自己的教学情况有更好的了解，并对下一阶段的教学进行更准确的判断。与此同时，借助系统的数据可以判断学生的学习状况，同时也可以分析相关原因。由此可见，教育信息化所带来的变化是巨大的。

阶段性的测评在对教师实际教学效果进行评价的同时，一定程度上能反映学生的学习情况。经验与科学研究证实，测评所传递的讯息能够让教师和学生知道自身的教学与学业状况。教师能够通过反馈的信息调整教学计划，从而调整教育活动，以便更高效地工作并达到设定的目标。

作为初中一线数学教师，在阶段性测评中要能常态化地利用信息技术手段，较为准确地收集测评数据，并通过及时分析数据改进、巩固教与学，以达到助力精准教学的目的。本文依据一线教学数据，着重阐述教师如何透过学生阶段性测评数据分析助力精准地进行试卷讲评，以达到学生和教师对自己学习或者教学有更明确认识的目的。

一、根据一分三率对教学进行整体评价

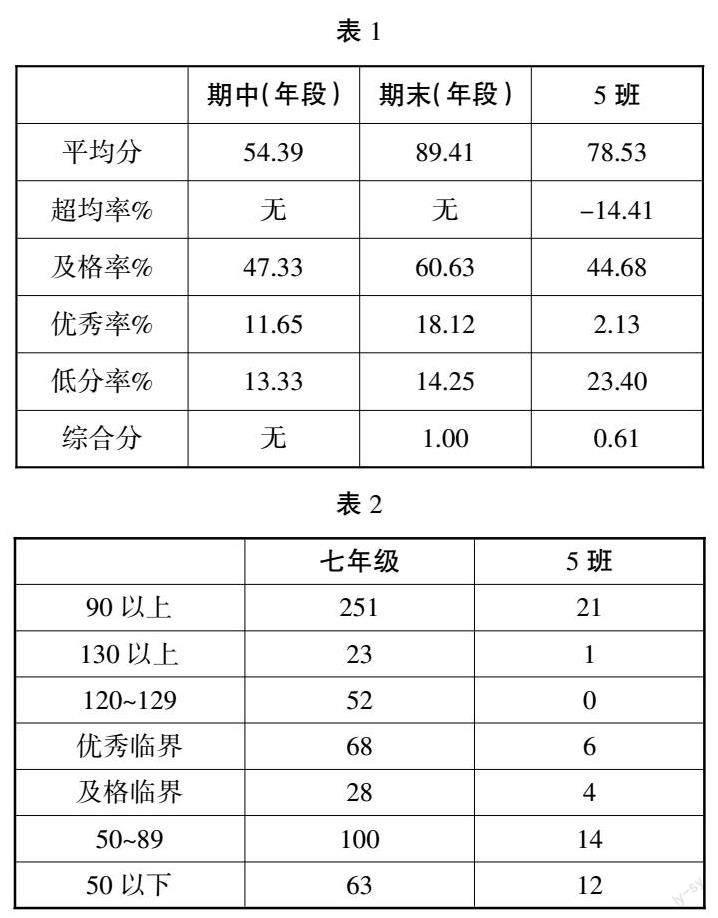
平均分主要是指依据数据的平均数反映实际的平均水平，在日常生活中有极为广泛的应用。结合实际情况来看，教师通过分析班级以及年级的平均分差异，可大致了解自己所教班级在年段中的学业水平。以七年级为例（见表1），在2022年1月期末测评中，年段均分为89.41，其中六个班级高于年段均分，三个班级低于年段均分。大多数班级与年级整体均分相比分差都在5分以内。而5班的成绩相比较于年段均分来说要低，具体分差高达11分。对比2021年4月阶段性测评可发现，这个班与年段均分的分差，在两个月的时间内扩大了8分。而其他班级与年段的分差基本不变。在此得出以下结论：教授5班的教师需综合考虑各方面因素，对本班的数据进行细致分析。

以下分析均以5班为例。以120分及以上为优秀率的评判标准，该班的优秀率低于年段所有班级但相较于上次测试，实现了零的突破（见表2）。由此可见，导致该班平均分差距大的因素中，优秀率是其中一个。以90分及以上为合格率的评判标准，该班的合格率比年段平均水平低了将近15个百分点（见表1）。由此可见，合格率低是导致该班平均分差距大的重要因素。

另外，从上表中年段的各分数段得分来看，该班的120～129这个分数段的人数为0，需要找到突破口，这样可以提升该班学生学习数学的信心。

通過以上分析，该班的教师在下一阶段教学中需在教学设计和教学实施上侧重“四基”的夯实巩固。一定要认真确定教学目标和内容，分析教学重点和突破教学难点的方法，以及明确各要点的层次关系，并邀请经验丰富的教师进行跟班听课和评课。

经过四个月的努力，在2022年5月的阶段性测评中，该班与年段均分的差距从原来的11分缩小为不到8分;相较于年段均值来说，优秀率差距相比以往有所缩小，合格率差距从低于年段15个百分点缩减为不到9个。通过以上分析，该班教师在教学中，仍需要继续加强“四基”的夯实巩固;需采取有效措施确保合格临界生养成良好的学习习惯，使其对学习产生兴趣，认真完成课堂作业，这是极为重要的。

二、根据小题得分情况，查找薄弱教学点

一分三率只能反映数据的整体情况，对教学进行整体评价，而查找具体的薄弱教学点，则需要通过小题得分的对比分析。教师应对比试卷小题得分率，找出偏差较大的题，分析失分原因。

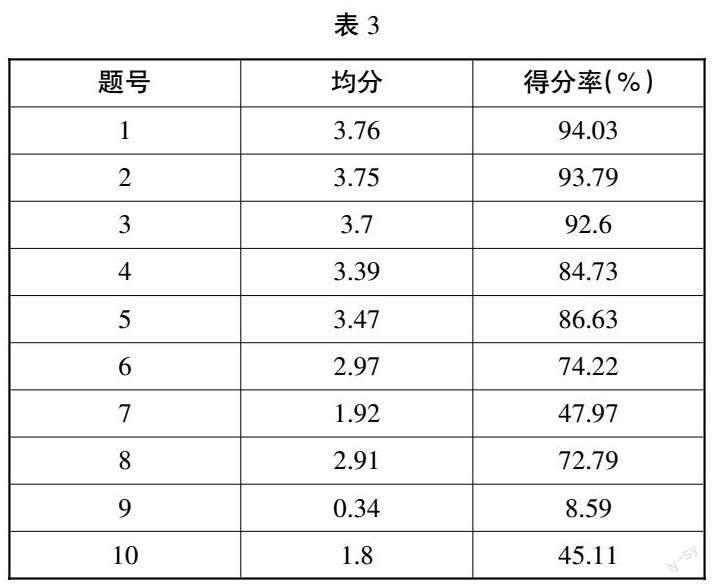
仍以该次的阶段性测评为例，先来看选择题。第7题、9题和10题的得分率远低于其他题目。

选择题得分情况（见表3）。

7.若a，b互为相反数（a≠0），则ax+b=0的根是（  ）

A.1 B.-1 C.1或-1 D.任意数

反思这三题平时的相关教学，以第7题为例：第7题反映了学生的分析能力较差。无论是课堂教学，还是例题练习，教师对计算的算法强调较多，对公式也仅局限于使用公式进行计算;学生未重点关注字母本身所表达的意义，在结构理解方面也有所欠缺。这就要求教师在后续的教学中进行补偿，同时进行平行性测评，以检测补偿教学的效果。

再来看看填空题得分情况（见表4）。

12.用两个钉子就可以把木条固定在墙上，用到的数学原理是               。

14.一个角的余角比它的补角的三分之二还少40°，则这个角为       度。

对于这个班来说，12、14题这样的基础问题的作答情况不好，得分率低于50%。第12题这样的问题在教师眼里是送分题，认为不需要进行讲评，可是学习习惯较差的学生就拿不到分数。说明这个班级一半的学生学习习惯较差，听课效果也较差。那么，教师就应该在这个班的学习习惯上下功夫。第14题主要是用代数方程思想来解几何问题。平时作业中虽有训练，但还是有一半学生无法掌握。根据改卷教师和学生的访谈情况，总结原因：看看学生的思路卡在哪里，再进行对症下药。平时更应该针对这样的题目多进行补偿性练习。

然后是解答题的薄弱点。具体得分情况见表5。

从得分率和均分来看，第22题是最需要进行反思的。

22.已知：如图，点A，点B，点D在射线OM上，点C在射线ON上，∠O+∠OCA=90°，∠O+∠OBC=90°，CA平分∠OCD.请说明∠ACD=∠OBC.

请将下面的说理过程补充完整。

解：因为∠O+∠OCA=90°，∠O+∠OBC=90°，

所以∠OCA=∠ .（理由： ）

因为CA平分∠OCD

所以∠ACD= .（理由： ）

所以∠ACD=∠OBC.

[A][B][C][D][O][N][M]

第22题图

本来这样的题目对七年级学生来说不算难，但是得分率却低于教师的期望值。根据改卷情况，这说明学生表达的严谨性还仅停留在模仿层面，未能形成严谨表达的能力。被扣2分的学生，大多数是不能完整书写定理，出现错别字或者用自己的语言表达或定理语言表达错误，这其中有不少是学优生。因为无论是新课学习阶段，还是单元测评阶段以及平时的阶段性测评，对几何初步部分定理的简单应用均呈现良好的反馈效果。而课堂抽测的定理文字表达也反馈优秀。那么，是什么原因导致日常教学过程中的反馈与阶段性测评中的反馈出现如此大的偏差呢？

通过学生访谈及教师反思，找出以下原因：（1）期末复习以两个代数单元为主，部分学生在学习几何定理的时候偏重机械记忆，缺乏理解。（2）平时教学中，定理的文字语言往往让学生口答，导致学生在默写的时候出现错字。（3）教师凭经验认为学优生在这方面不存在问题，加之课堂提问机会有限，此类问题通常提问中等生和学困生，但还有一部分学生没有被提问到。

根据以上分析，后续教学需要做出以下改变：（1）结合所学知识，如图形语言等进行理解与转化，这样做的主要目的是增强学生对几何语言的理解，从而更好地掌握知识。（2）课堂实时检测方式口答、笔答等要灵活多变，提问对象也要更加随机、普遍。

三、通过分析小题得分率和错误原因，提升教师的命题水平

例如，在2022年4月的单元测评中，考了这样一道题：下列调查适合全面调查的是（  ）

A.了解福州市民消费水平

B.了解某班学生每周体育锻炼的时长

C.了解福州市中学生的视力情况

D.了解一批节能灯的使用寿命

本题得分情况见表6。

依据表6数据可以得出以下结论：该题的得分率相较于命题者的预期来说要低。作为易学易会的知识点，出现这种情况的原因值得研究。查看错选率可知，错选C项的学生居多。走访发现：学生在测评前一周参加了由市教育局组织的视力筛查，故而认为C项正确。集备组在进行命题反思的时候提出，今后命题要注意避免两可的情况;同时和学生解释，要以考生为调查人员进行思考。

经过上述分析得出以下结论：一线教师在教学评价过程中常常会选择作业检查等形式，往往更多依赖教师的主观感受或经验，同时在评价样本的选取上不够全面。一月一次或两月一次的阶段性测评，实操性、可持續性强。利用信息技术手段，能较为准确地收集测评数据、及时分析数据，能对教师教学以及命题进行更为准确的诊断，达到助力教学效率提升的目的。

随着大数据时代的到来，相信数据会在教学中发挥更广泛的作用。

参考文献：

[1]曹一鸣，李俊扬，秦华.我国数学课堂教学评价研究综述[J].数学通报，2011，50（8）：1-5.

[2]乔景肖.论如何实现中学数学课堂有效评价[J].试题与研究，2021（4）：127-128.

（作者单位：福建省福州市二十五中）

编辑：常超波