考虑冲击与齿根应力的齿轮接触稳定性分析

2023-07-27何延晓王承登伍宏建刘威刘鹏

机床与液压 2023年13期

何延晓，王承登，伍宏建，刘威，刘鹏

(重庆交通大学机电与车辆工程学院，重庆 400074)

0 前言

渐开线圆柱齿轮传动作为主要的传动方式之一，广泛应用于航空航天、船舶海洋、交通运输等重要行业。接触稳定性是评价齿轮传动品质的关键指标，稳定性低的齿轮系统会导致齿轮使用寿命降低、安全可靠性差、各激励耦合作用明显、振动噪声显著等问题。因此，对齿轮系统接触稳定性展开研究具有重大理论意义及工程应用价值。

现已有大量学者对齿轮系统啮合特性展开研究[1-3]。部分学者为探究齿轮接触特性，对其接触状态进行了以下分析：梁栋等人[4]推导了齿轮空间共轭曲线副啮合方程，对接触迹线进行了计算与分析；段文浩等[5]研究了不同螺旋角下双圆弧齿轮的啮合特性，分析了螺旋角对啮合特性的影响；王羽达等[6]考虑齿间分配载荷，对齿轮进行了承载接触分析。

为探寻齿轮稳定性的影响因素及其贡献度，部分学者对不同物理量与激励进行分析，研究其对接触特性的影响。刘明勇等[7]应用有限元法分析了斜齿轮的塑性变形、材料线性强化、温度及摩擦等因素对齿轮啮合特性的影响，并用实验进行验证；万志国等[8]建立齿轮系统动力学模型，研究了齿侧间隙、时变刚度、啮合阻尼对齿轮系统动力学特性的影响；陈安华等[9]建立了动力学模型，探究了啮合阻尼、支承阻尼、重合度与支承刚度对齿轮系统动力稳定性的影响；曲伟等人[10]分析了不同转速与负载下减速器齿轮的变形量与最大等效应力的变化，并得出相应的变化规律。

综上可知，关于齿轮接触特性以及啮合稳定性的研究众多，且已取得一定的研究成果。大多学者均是对各因素进行单独影响分析，缺少对不同工况下啮合冲击、齿根应力等各因素间的演变耦合规律进行分析。因此，本文作者以一对机匣齿轮为分析对象，应用能量守恒定理计算不同工况下齿轮啮合冲击，应用修改后齿根应力算法计算不同转矩下的危险截面齿根应力，然后通过有限元法计算实际工况下齿轮动态接触力，并与理论值对比，验证其可靠性。探究不同工况下齿轮接触力稳定性情况，结合啮合冲击与齿根应力，综合分析其影响关系，得出齿轮接触稳定性受转速、转矩、啮合冲击、齿根应力的影响规律，为齿轮系统最佳工况选取及接触稳定性优化提供参考。

1 理论方法

1.1 啮入冲击理论

啮合冲击包括啮入冲击与啮出冲击，由于啮入冲击影响远远大于啮出冲击，因此主要针对啮入冲击进行分析。

理想状态下，主被动齿轮基圆齿距相等，齿对沿啮合线正常啮合，但由于齿廓误差与轮齿受载变形等因素影响，齿距发生微量变化，主从动基圆齿距不等，啮入点偏离啮合线致使线外啮合。而未在啮合线内正常啮合齿对沿瞬时啮合线方向速度不等，产生冲击速度，导致啮入冲击。如图1所示，Pb1与Pb2分别为主从动轮瞬时齿距、啮入产生的相对齿距差ΔPb导致点A线外啮合，出现冲击速度vs，啮入冲击在点A产生。

图1 啮入冲击示意

首先确定冲击点位置，应用反转法得到啮入冲击点几何位置图，如图2所示。几何间隙角φ可由变形量求得：

图2 冲击点几何位置

φ=δΣ/rb2

(1)

δΣ=δ1+δ2+δc

(2)

式中：δΣ为前一齿对沿啮合方向总变形量；δc为前一齿对齿面接触变形量；δ1、δ2为前一齿对沿啮合方向产生的挠曲变形量。

由几何关系可得：

(3)

(4)

(5)

γ1=α-αB

(6)

γ2=αa2-α

(7)

ε=invαA-invαB

(8)

式中：αB为理论啮合点B的压力角；k为传动比；a为中心距；rO1A为冲击半径；α为齿轮副压力角；θ1、θ2为主从动轮反转角度；αA为冲击点压力角；ε为主动齿上提前啮入角度；αa2从动轮齿顶圆压力角；ra2为从动轮齿顶圆半径；γ1、γ2位置如图2所示。

联立式(1)—式(8)可求解冲击半径，即确定了冲击位置。在冲击瞬时可做如图3所示等效瞬时基圆与啮合线，则啮入冲击速度vs为

图3 等效基圆

(9)

(10)

(11)

(12)

式中：m1、m2分别为主、从动轮在瞬时啮合线上的诱导质量；J1、J2分别为主、从动轮的转动惯量；rh1、rh2分别为主、从动轮轮毂内孔半径；ρ为密度；b为齿宽。

根据冲击力学理论，每片直齿轮副之间产生的最大变形量δs、最大冲击力F及冲击能量Ek之间的关系可以表述为

(13)

式中：qs为齿轮副啮入冲击点的综合柔度，qs=q1+q2+qh，q1、q2分别为主、从动轮齿在啮入冲击点处的弯曲变形柔度，qh为轮齿在啮入冲击点处的接触柔度。

由式(13)可求齿轮副最大冲击力的表达式：

(14)

1.2 齿根应力计算方法

目前齿轮齿根应力主要应用渐开线圆柱齿轮承载能力计算方法GB/T 3480计算，但是对于变压力角滚刀加工的齿轮，此方法会出现较大偏差。因此，文中应用修正后的齿根弯曲应力计算方法进行求解。

将齿轮加工滚齿运动等效为齿轮固定不动、滚刀绕齿轮做纯滚动运动，如图4所示。

图4 齿轮与滚刀啮合示意

图中，点A为滚刀与齿轮瞬时接触点，点D为滚刀顶部圆角圆心，AE为齿根接触点A处曲率半径，点P为滚刀与齿轮速度瞬心，ψ为P与齿轮中心连线和齿形对称线间夹角，L为滚刀节距。据滚齿原理可知弧长BP等于GP，因此根据图中几何关系得：

r×ψ=L/2+(hfp-ρfp)/tanα1

(15)

γ+ψ=α1

(16)

以齿轮圆心为坐标原点建立直角坐标系，则点A的坐标可以表示为

(17)

Euler-Savary公式可以表示共轭曲线与瞬心线曲率半径的关系，一般形式为

(18)

由于两瞬心线内切，则式(18)中曲率半径取负值。将此式应用到滚齿运动中，齿根各点的曲率半径可表示为

(19)

令γ=30°，由式(15)(16)可求解α1，从而求得齿根危险截面处曲率半径。

图5所示为轮齿载荷作用示意，αFen为轮齿啮合外界点载荷作用角，γe为外界点处齿厚半角，图中点C坐标值可由式(3)求得。由图中关系可知：

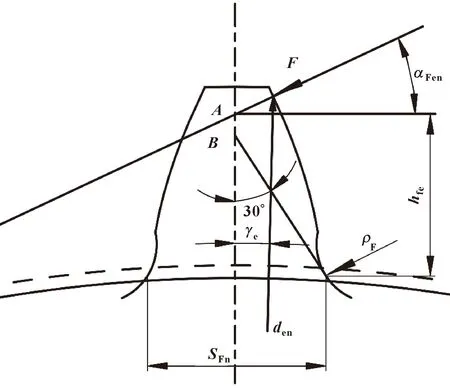
图5 载荷作用于单对齿啮合区外界点示意

SFn=2x

(20)

hFe=0.5dencosγe-0.5densinγetanαFen-y

(21)

式中：SFn为危险截面齿厚；hFe为弯曲力臂；den为轮齿啮合外界点直径。

应力修正系数Ys与齿形系数YF为

(22)

(23)

式中：L为齿根危险截面齿厚与弯曲力臂比值；qs为齿根圆角参数；α为齿轮分度圆压力角；m为模数。

至此，经修正的齿轮齿根应力σF可求得：

(24)

σF=σF0KAKvKFβKFα

(25)

式中：σF0为齿根应力的基本值；Yβ为螺旋角系数；Fτ为齿轮分度圆上切向力；KFα为弯曲强度计算的齿间载荷分布系数；KA为使用系数；Kv为动载系数；KFβ为弯曲强度计算的齿向载荷分布系数。

2 接触力数值计算

齿轮啮合在考虑摩擦、齿侧间隙及齿轮各内部激励等因素共同作用下为强非线性系统，且各激励作用下产生的振动响应又反作用于各激励，造成复杂的多非线性耦合转化反馈现象。因此，擅长进行几何非线性分析的有限元法能够更准确地对此类问题求解，文中用LS-DYNA的显式直接积分法，进行连续啮合齿轮动态接触力求解。

首先建立齿轮啮合分析精确三维模型，然后对其进行有限元网格离散，得到渐开线直齿轮传动有限元动态啮合分析模型如图6所示。齿轮外部使用Solid164三维实体单元划分，因Shell63单元具有旋转自由度，方便工作载荷添加，故齿轮内圈表面选用刚性壳体单元Shell63，实体单元与刚性壳体单元共用节点。为还原真实工况，对齿轮体内孔的所有平动自由度进行了约束，对齿轮除绕轴外的所有转动自由度进行了约束，在主动齿轮内圈添加驱动转速，从动齿轮内圈添加负载扭矩，在所有齿对间建立接触关系。

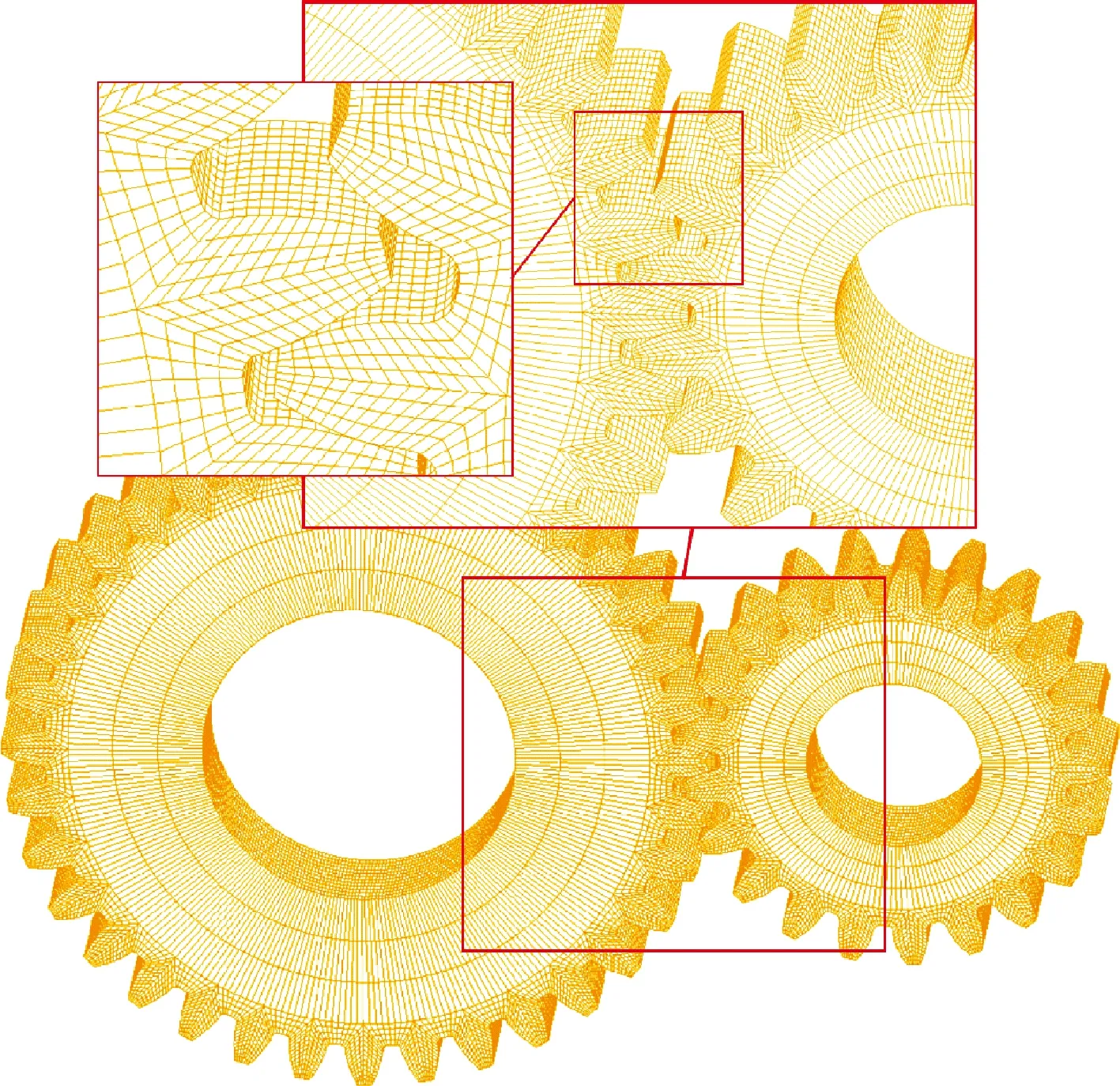
图6 动态啮合模型

文中分析对象为一对航空机匣齿轮，齿轮参数如表1所示。为模拟真实启动状态，加载过渡时间为3对啮合齿时间，求解时间设置为主动轮转动一周时间，此时齿轮啮合已达相对平稳状态。以转矩150 Nm、转速1 500 r/min为例，载荷历程曲线如图7—图8所示。

表1 齿轮参数

图7 加载转速

图8 加载转矩

求解结束后提取从动轮角速度如图9所示，可知：2 ms加载结束后，从动轮转速在理论值269.28 rad/s附近波动，验证了转速的合理性。

图9 从动轮动态角速度

提取齿轮稳定运行后齿对动态接触力如图10所示，计算得数值计算接触力平均值为3 031.287 N，与理论解析值2 956.05 N误差为2.5%，在各激励耦合作用下，数值解略高于理论值，但误差在合理范围内，故该数值解析法合理性得以验证。

图10 动态接触力

3 变工况下齿轮接触稳定性分析

为揭示不同工况下啮合冲击、齿根应力、接触稳定性间的内在关联与影响关系，将三者进行对比分析，以便进一步进行最优工况的选取及接触稳定性优化方法研究。

针对文中研究对象即机匣齿轮设置5个不同转速，分别为500、1 000、1 500、2 000、2 500 r/min，设置5个不同转矩分别为50、100、150、200、250 N·m。

将第一节啮合冲击与齿根应力计算方法编为MATLAB程序，分别对不同工况下的啮合冲击力与齿根应力进行计算，得出如图11所示的不同工况下两指标变化规律。

图11 冲击力与齿根应力变化规律

图11(a)中，从动轮齿根应力大于主动轮，且主从动轮的齿根应力均随转矩增大而增大。由于转矩增大导致啮合力增大，因此齿根应力也随之增大，由图11(a)可知应力与转矩几乎成正比的关系。

由图11(b)(c)知，啮合冲击力随转速与转矩的增大而增大，且随转矩增大，冲击力的增大趋势减缓，而冲击力与转速几乎成正比关系增长。结合理论分析，当输入转矩增加，齿轮轮齿接触力增加，导致轮齿受载变形量变大，冲击速度变大，啮合冲击力增大。而转速增加会导致啮合冲击速度增大，因此啮合冲击力增加。

在研究工况对接触稳定性影响时，将转矩与转速分为2组进行讨论，第一组设置转速为1 500 r/min，转矩分别取50～250 N·m；第二组设置转矩为150 N·m，转速分别为500～2 500 r/min。第一组变转矩数值计算时变接触力如图12所示，通过接触力变化幅值与标准差衡量接触稳定性。

图12 变转矩接触稳定性分析

首先对第一组变转矩接触力进行分析，从图12中可以看出：转矩为50 N·m时接触力波动幅值很大，且一直有接触为0的情况，表明在此工况下齿轮啮合伴有脱齿现象产生，这是高速轻载工况所导致的，此工况下接触力标准差为807 N，稳定性较差；转矩为100 N·m时未见脱齿现象，动态接触力变化幅值有所降低，稳定性比50 N·m时有所改善；转矩为150 N·m时接触趋于相对稳定状态，标准差为495 N，稳定性最好。转矩为200 N·m与250 N·m时接触力变化幅值逐渐增大，接触力稳定性逐渐变差，但并未出现脱齿现象。综上分析可以得出接触稳定性随转矩变化规律：在高速轻载时，齿轮啮合易出现脱齿现象，且接触稳定性较差，随着转矩增大齿轮接触逐渐趋于稳定，稳定后随转矩不断增大，接触稳定性渐渐降低，但重载情况下，不会发生脱齿行为。

第二组变转速数值计算时变接触力如图13所示。由图可知：在正常负载下，所取转速变化范围内未见脱齿现象，转速为500 r/min时接触稳定性较差，在转速为1 000 r/min时接触稳定性最好，其余转速下稳定性次之，但并未出现稳定性极差的情况。综上分析可得接触稳定性随转速变化规律：在正常负载情况下，合理范围内变转速不会造成脱齿行为，对于负载来说存在某一转速范围使接触稳定性达到最佳，其余转速接触稳定性稍次之，且转速对接触稳定性影响小于转矩。

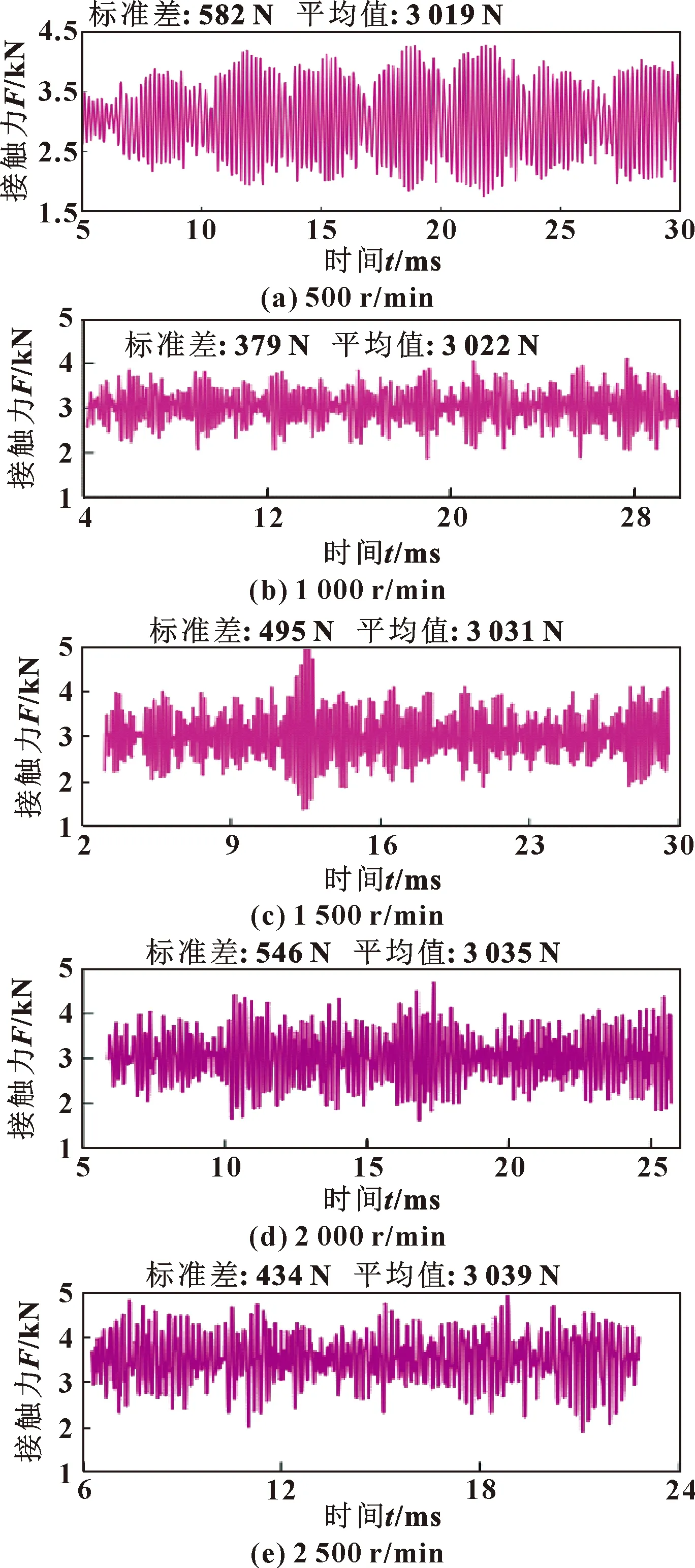
图13 变转速接触稳定性分析

接触力标准差与平均值随工况变化规律如图14所示，转矩变化引起标准差的变化幅值大于转速变化，且转矩与接触力平均值几乎成正比例关系，而转速对平均值影响不大，转速与转矩都存在某一最佳范围使标准差最小。

图14 接触力标准差与平均值变化规律

结合变工况下齿根应力与啮合冲击变化规律对齿轮接触稳定性进行分析，由图11与图14可知转矩变化会引起接触力平均值、齿根应力与啮合冲击共同变化，说明转矩变化导致多个状态量共同变化，互相耦合演化，同时作用于接触稳定性，使接触稳定性受转矩影响较大；而转速变化对实际接触力变化影响较小，仅使啮合冲击增大，影响接触稳定，故接触稳定性受转速变化影响较小。