基于改进人工水母搜索算法的电液伺服系统控制研究
2023-07-27付荣赫秦泰张奇邢吉生
付荣赫,秦泰,张奇,邢吉生
(北华大学电气与信息工程学院,吉林吉林 132021)
0 前言
电液伺服系统因高度可控性和高效性已被广泛应用于工业制造、航空航天等领域[1],系统能否稳定运行取决于其传动部分是否稳定,进而直接影响到其实际应用。因此,运用自动化技术、智能算法等实现电液伺服系统精确、稳定控制,对提升系统的运行效率以及产品的质量等具有非常重要的意义。
电液伺服系统主要由动力部分和电信号处理部分组成,可用小功率电信号来控制大功率传动元件[2]。但它是一个复杂的非线性系统,含有时变不确定性和扰动性,PID传统控制方法受自身局限性约束,很难在复杂系统中整定出理想的最优值,使得其控制效果不佳,已不能满足系统所需的控制要求[3]。
现如今,随着学者们对智能算法的深入研究,众多群智能算法被引入到PID参数整定优化问题中[4],但算法中的问题也逐步显现出来。比如人工水母搜索[5](Artificial Jellyfish Search,AJS)算法存在易陷入局部最优等问题,为了解决这些问题,本文作者提出将蝴蝶优化算法(Butterfly Optimization Algorithm,BOA)中的随机移动概念引入AJS算法中优化PID参数,在保留算法简单、易实现的基础上,通过增强个体位置多样性提高算法的精度、全局搜索能力等。
1 电液伺服系统数学模型
在工业制造领域,电液伺服系统具有反应速度快、灵敏性高等优点,在注塑机运行时提供较准确的控制。系统主要由指令装置、液压缸、传感器、伺服电磁阀和动力装置组成[6],结构如图1所示。
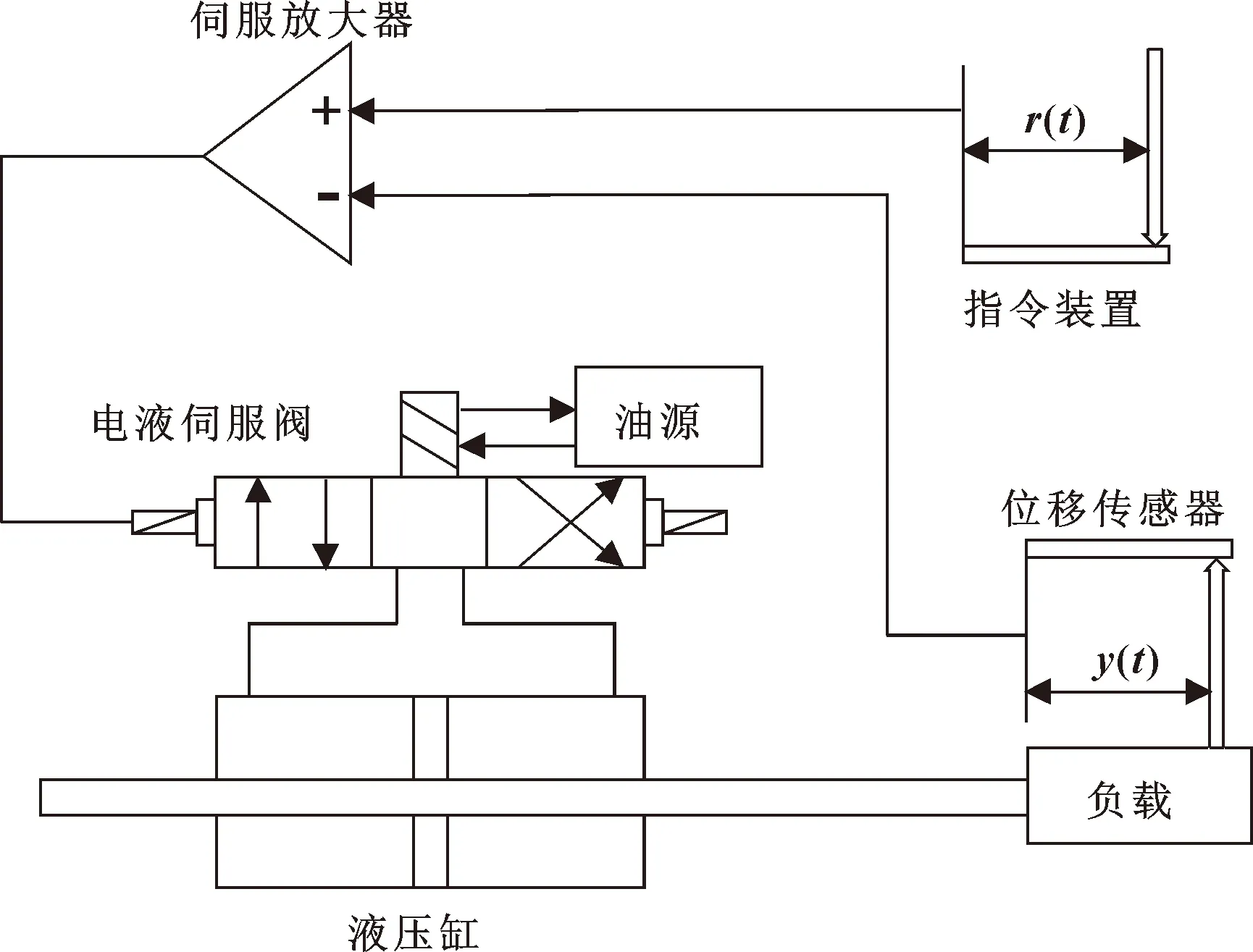
图1 电液伺服系统结构
该系统由指令装置给定指令电位,输入位置信号经控制器、伺服放大器等到达电液伺服阀,位置反馈将输出位置信号反馈回比较元件,产生误差信号后输入控制器,进而控制液压缸的位移[7]。其控制原理如图2所示。
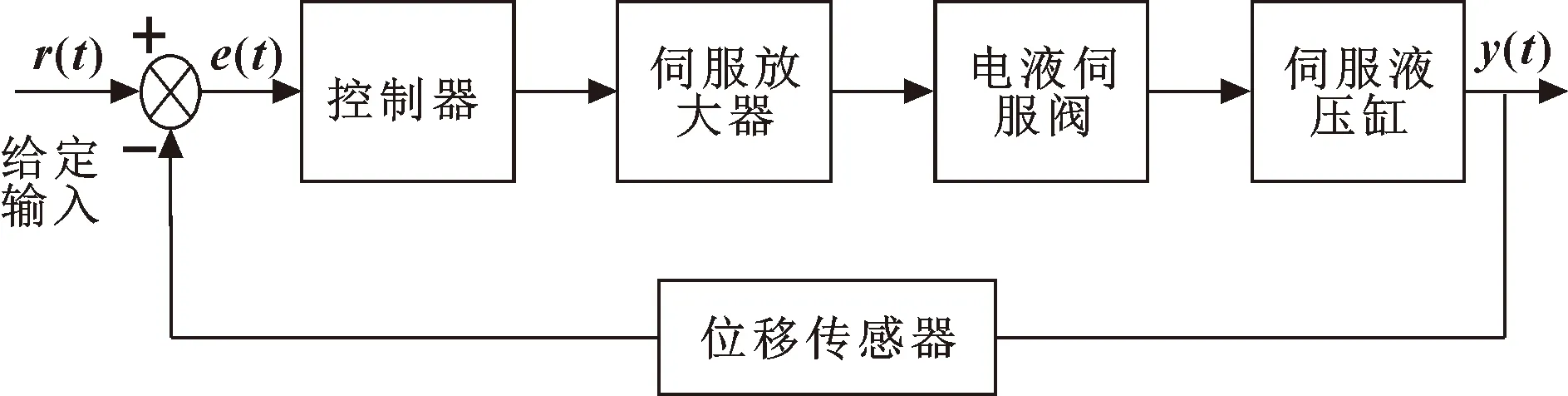
图2 系统控制原理
电液伺服系统的运动微分方程[2]为
(1)
(2)
xv=KvKSu
(3)
式中:Ap为活塞面积;xp为活塞位移;Ct为总泄漏系数;p1为负载压差;Vt为总压缩容积;KQ为流量增益;xv为阀芯位移;Kc为压力系数;βe为弹性模量;mt为活塞上总质量;cp为黏性阻尼系数;FL为负载力;k为弹簧刚度;Kv为控制器增益;KS为伺服阀增益;u为控制电压信号。
在控制电压u的作用下,其动态方程[1]为
(4)
式中:ξ为阀门阻尼比;ωn为阀门固有角频率;η为阀门增益。
创建良好的系统数学模型,是获得传递函数的关键[8]。对系统的输入以及输出的数学模型进行分析,得出伺服阀的传递函数为
(5)
2 人工水母搜索算法
人工水母搜索算法(AJS)是模拟自然界水母觅食搜寻行动的一种随机搜索算法。在水母觅食过程中,涉及到水母与洋流、水母在水母群中的运动(主动运动和被动运动),这些运动之间通过时间控制机制进行切换,以及汇聚成水母群的过程[9]。
在AJS算法中,存在以下2种假设:水母可以跟随洋流,也可以在群体内部移动,而时间控制机制管理着这些移动类型之间的转换;水母在海洋中移动寻找食物,它们更容易被吸引到食物供应量更大的地方。
2.1 洋流对水母位置的影响
洋流中含有大量的营养物质,因此水母才被吸引过来。洋流的方向由海洋中每只水母到目前位于最佳位置的水母的所有向量平均值决定,公式如下:
(6)
t=X*-df
(7)
df=ecu0
(8)
其中:npop为水母数量;X*为当前水母种群的最优位置;ec为控制吸引力的因子,由式(9)确定;u0为所有水母的平均位置;df为目前水母最佳位置和所有水母的平均位置之间的差异,由式(10)确定。
ec=β·rand(0,1)
(9)
df=β·rand(0,1)·u
(10)
每只水母的新位置:
Xi(t+1)=Xi(t)+rand(0,1)·t
(11)
将式(7)、式(10)代入式(11)中,即:
Xi(t+1)=Xi(t)+rand(0,1)·(X*-β·
rand(0,1)·u)
(12)
式中:β为分配系数,取值为3。
2.2 水母群对水母位置的影响
类型A运动是水母围绕其位置的运动,每个水母的相应更新位置:
Xi(t+1)=Xi(t)+γ·rand(0,1)·(Ub-Lb)
(13)
式中:Ub和Lb是搜索空间的上限和下限;γ为运动系数,取值为0.1。
为了模拟B型水母的运动,随机选取一只水母j作为感兴趣的水母,水母i至选定的水母j的矢量确定其运动方向。当选定的水母j所在地点的食物数量超过水母i所在地点的食物数量时,则后者朝前者移动;反之,则后者远离前者。因此,每只水母都朝着更好的方向移动,寻找群体中的食物。水母的运动方向和更新的位置公式如下:
S=Xi(t+1)-Xi(t)
(14)
whereS=rand(0,1)·D
(15)
Xi(t+1)=Xi(t)+S
(16)
(17)
时间控制公式如式(18)所示:
(18)
式中:t为迭代次数;nmax为最大迭代次数。
2.3 种群初始化
水母位置初始化如式(19)所示:
Xi(t+1)=ηXi(1-Xi) 0≤X0≤1
(19)
式中:Xi为第i类水母的Logistic逻辑混沌值;X0∈[0,1]为水母初始位置范围,但X0≠0,0.25,0.75,0.5,1.0,η=4.0。
2.4 边界条件
海洋分布在全球各地,因此当水母移出有界的搜索区域时,它会回到相反的界限:
X′i,d=(Xi,d-Ub,d)+Lb(d) ifXi,d>Ub,d
(20)
X′i,d=(Xi,d-Lb,d)+Ub(d) ifXi,d (21) 式中:X′i,d为更新后的水母位置;Xi,d为第i只水母在d维的位置;Ub,d和Lb,d为搜索空间的上下限。 针对AJS算法存在易陷入局部最优等问题,提出改进策略,将蝴蝶算法[10]融入到AJS算法中,来增强全局搜索能力和收敛精度,形成改进人工水母(Improved Artificial Jellyfish Search,IAJS)算法。此次改进策略是将蝴蝶算法里蝴蝶全局搜索阶段的思想引入到AJS算法中,对其个体位置进行更新。此方法可增强类型A运动水母位置的多样性。位置更新公式如式(22)所示: Xi(t+1)=Xi(t)+γ·rand(0,1)·(Ub-Lb)+ (22) 式中:g*为目前为止的最优解;fi为水母的发光点;r∈[0,1],为随机数[11]。 算法的详细步骤为:(1)初始化水母种群;(2)评估适应度值确定初始最优位置;(3)更新时间控制参数c(t);(4)根据洋流更新水母位置;(5)更新运动类型,分别更新类型A和B的水母位置;(6)重新评估适应度值及更新水母最优位置;(7)判断是否满足最大迭代次数,若满足,则输出最优位置和全局最优解,否则,返回步骤(3)重新迭代计算。 PID控制由PID控制器和被控对象所构成,而PID控制器由三部分构成,分别为比例、积分和微分等,其应用格外广泛,控制规律如式(23)所示: (23) 式中:e(t)是系统误差;Kp、Ki、Kd分别对应PID控制器中3个部分的系数,通过调整这3个系数,找到其最优值,就能得到较好的控制成果,达到改善控制性能的目的[12-15]。将IAJS算法用于PID参数整定原理如图3所示。 此次以某型号注塑机为例,将系统主要参数代入式(5)所示的传递函数中,得到系统仿真模型为 (24) 此系统为典型的二阶系统,在MATLAB软件中仿真控制系统的传递函数,它在Simulink环境下仿真图如图4所示。 图4 Simulink环境下PID仿真图 为验证文中所提出算法的优劣性,分别选用IAJS、AJS和PSO算法对系统进行PID控制器的参数优化。为了方便比较3种算法,设置其输入为单位阶跃信号,仿真时长设为15 s,采样时长为0.001 s,迭代次数为100次。 采用不同算法进行多次迭代后输出其适应值收敛曲线如图5所示。可知:随着迭代次数的增加,IAJS算法在迭代次数为23次时,适应值收敛并精度较高,而AJS和PSO算法分别迭代到26次和28次时适应值收敛,因此IAJS展现出了精度高等优势。 图5 算法收敛曲线 输出IAJS算法优化PID参数变化曲线如图6所示。Kp、Ki、Kd这3个参数大约经23次迭代后输出最优值,IAJS算法在前期表现出卓越的全局收敛能力,并且于迭代次数较少的情况下能得到较高的精度。 图6 IAJS优化PID参数曲线 将3种算法优化所得的参数值依次代入控制系统的PID控制器中,并在MATLAB中运行,得出响应曲线如图7所示。可知:标准PSO的上升时间短,进而导致PSO的响应速度快于IAJS算法,但在超调量、稳态误差等方面IAJS明显更少。 图7 阶跃响应输出曲线 此外,IAJS算法到达稳定所用的调节时间为2.12 s,优于AJS和PSO算法稳定的调节时间2.45 s,因此系统的调节速度更快,能很快达到稳定状态。经过IAJS优化的PID最佳参数,选出的3个K值恰当,将调节时间和超调量等优化到尽可能小,使系统得到良好的控制效果,因而证明此方法的可行性。 在t=10 s时引入一个单位的阶跃扰动,输出响应曲线如图8所示。可知:系统受到阶跃扰动后都会产生短暂的震荡,扰动消除后系统逐步恢复稳定,文中所提出的IAJS算法相比于其他2种算法有较出色的抗干扰能力,同时也展现出更优越的控制效果。 图8 加入阶跃扰动后响应曲线 文中以电液伺服系统为研究对象,针对常规PID控制存在参数调节时间长等问题,提出了运用IAJS优化PID参数的方法,并验证了引入蝴蝶随机移动概念后的IAJS算法通过增强位置多样性后能有效改善AJS算法易陷入局部最优等缺点的可行性。通过对比3种算法参数整定优化的结果,在控制效果、调节时间、性能指标和稳定性等方面,IAJS算法比其他2种方法效果更好,显著提高了系统的稳定状态,有效地提升了系统的性能和运行稳定性。这就使得其在航空航天、机床控制以及振动环境模拟系统等领域应用更为广泛,对于减少设备的过载损坏、提升设备的使用寿命以及节能减排等方面有着广阔的应用前景。3 改进人工水母算法
3.1 改进策略
3.2 改进人工水母算法PID设计
4 仿真结果与对比分析

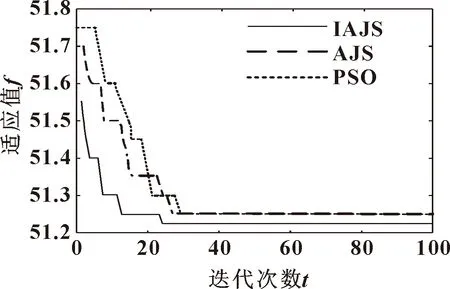
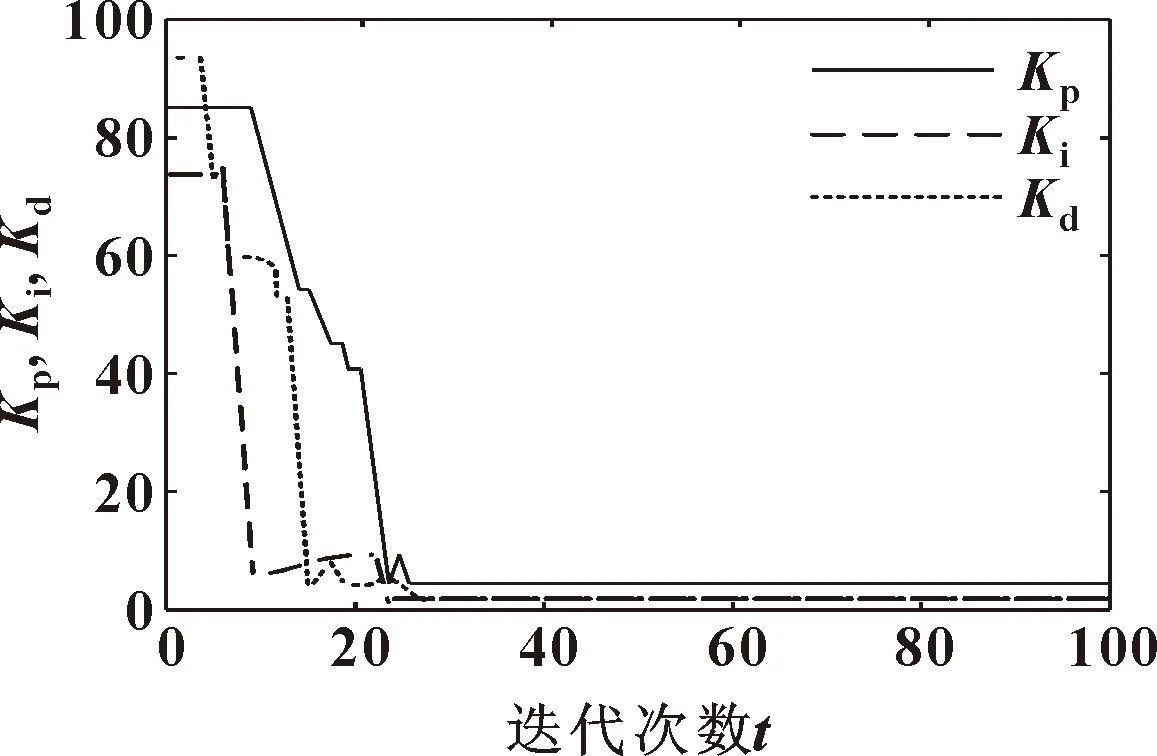
5 结论
