比例控制回路压力补偿分析
2023-07-27郭锐牛雯雯王涛王建伟蔡伟
郭锐,牛雯雯,王涛,王建伟,3,蔡伟,4
(1.燕山大学河北省重型机械流体动力传输与控制重点实验室,河北秦皇岛066004;2.航天发射场可靠性技术重点实验室,海南海口 571126;3.燕山大学先进锻压成形技术与科学教育部重点实验室,河北秦皇岛 066004;4.河北省特种运载装备重点实验室,河北秦皇岛 066004)
0 前言
液压传动在工程机械中应用普遍,其控制技术决定了工程机械的整体性能。比例控制技术作为液压系统中常用的控制手段,为液压系统的固有参数(压力、流量等)提供了一种基于比例信号的线性控制手段[1]。比例控制技术通过与压力补偿单元配合,可以保证执行元件的速度不受负载波动的影响,提高系统速度的可控性,在一些对执行元件有速度调节、位置同步等要求的场合均有广泛应用[2-4]。在诸多控制手段中,采用压力补偿器对比例阀进行压力补偿的方式最为广泛。李明生等[5]将压力补偿阀应用到一种液控比例流量阀中,通过计算仿真表明该流量阀具备良好的流量控制特性,压力补偿阀提升了阀组整体的流量控制精度。华博等人[6]对一种比例提升阀组中各组件的机制、结构进行分析探究,其中压力补偿阀件在阀组中起到补偿压力、稳定流量的作用。陈革新等[7]探究了压力补偿阀对负载敏感多路阀微动特性的影响,通过改变压力补偿器的阀口结构提升了多路阀的微动特性。赵小龙等[8]探究了压力补偿阀在定量泵负载敏感回路中对卸荷冲击的影响,通过改变三通压力补偿阀参数及阀口结构提高了卸荷压力冲击抑制效果。这些研究都是基于单级压力补偿回路。由于该回路中补偿器的弹簧不具备压差的调节能力,导致补偿的压差为定值[9-10],这在一定程度上使得流量的控制范围受到限制,并且无法适应不同换向阀节流口压差设定值的需要。
本文作者旨在研究一种新型采用变压差压力补偿阀的补偿回路,基于压力补偿原理与电液比例控制理论搭建液压仿真模型,通过仿真对其运用时的特性进行分析。
1 压力补偿回路调速原理分析
一般比例阀的阀口流量公式如下:
(1)
式中:Cq为流量系数;A为阀口流通面积;Δp为阀口压差;ρ为油液密度。
在一般的调速回路中,负载总是处在时刻的波动中,会使执行元件的速度受到影响[11]。可利用伺服阀加以控制,但会使成本增加。相比于伺服阀,比例阀价格低廉,对油液污染敏感性较小,且可靠性更高。可通过在比例控制回路里使用压力补偿单元,弥补比例阀在该种调速回路中控制能力不足的缺点,利用比例信号控制开口实现对液压系统流量的无级调节。
2 定压差压力补偿回路的工作原理
压力补偿原理:如图1所示的定差减压阀与比例换向阀构成的简单回路,压力被分为3个部分:定差减压阀阀前压力p1,比例换向阀阀前压力p2,比例换向阀阀后压力p3。若油路中的压力损失忽略不计,略去液动力,在该回路中存在如下关系:
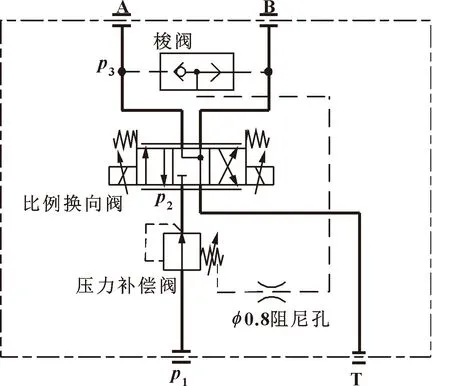
图1 压力补偿回路原理
p2AK=FK+p3AK
(2)
式中:FK为弹簧力;AK为阀芯作用面积。
即Δp1=p2-p3=FK/AK,当弹簧较软、调节位移又比较小时,补偿的压力近似为定值[12]。
压力补偿过程分析:由于负载变化导致负载端压力p3增大时,即弹簧腔压力信号增大,平衡被破坏,压力补偿阀阀芯有移动增大开口的趋势。定差减压阀的压差Δp1降低,在p1不变的情况下p2增大,阀芯创建新的平衡,保证换向阀压差不变;若负载的变化导致减压阀阀前压力p1增大,开始的瞬间阀芯不会移动,定差减压阀的压差Δp1不变,p2增大,无弹簧腔的压力信号增大,阀芯有移动关闭的趋势,导致定差减压阀的压差Δp1增加,p2慢慢降低恢复到原来值,阀芯重新创建平衡。
3 单级压力补偿回路仿真分析
基于定压差压力补偿回路的原理,利用AMESim提供的系统仿真平台搭建整个回路的液压模型如图2所示。为验证压力补偿回路是否能够有效缓解由于负载波动对于系统流量的影响,模型设置了2种不同的干扰信号来模拟波动的负载。仿真模型用可调的节流阀来代替比例换向阀,简化了回路的搭建,可调节流阀也是一种比例阀。
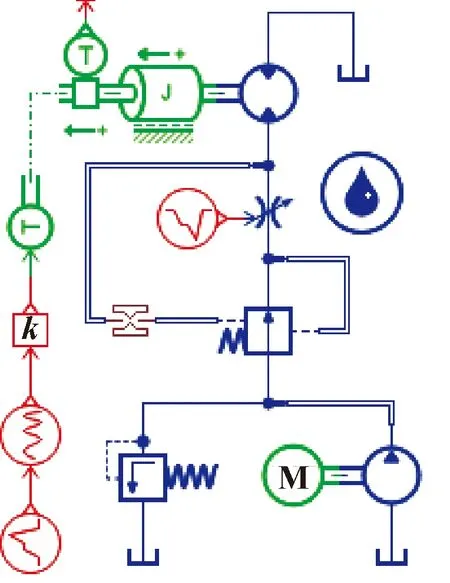
图2 单级压力补偿回路仿真模型
图3表示两种不同信号的建模方式仅在信号端有所不同。设置AMESim仿真参数,不同信号控制回路中各个元件初始值见表1。

表1 元件参数
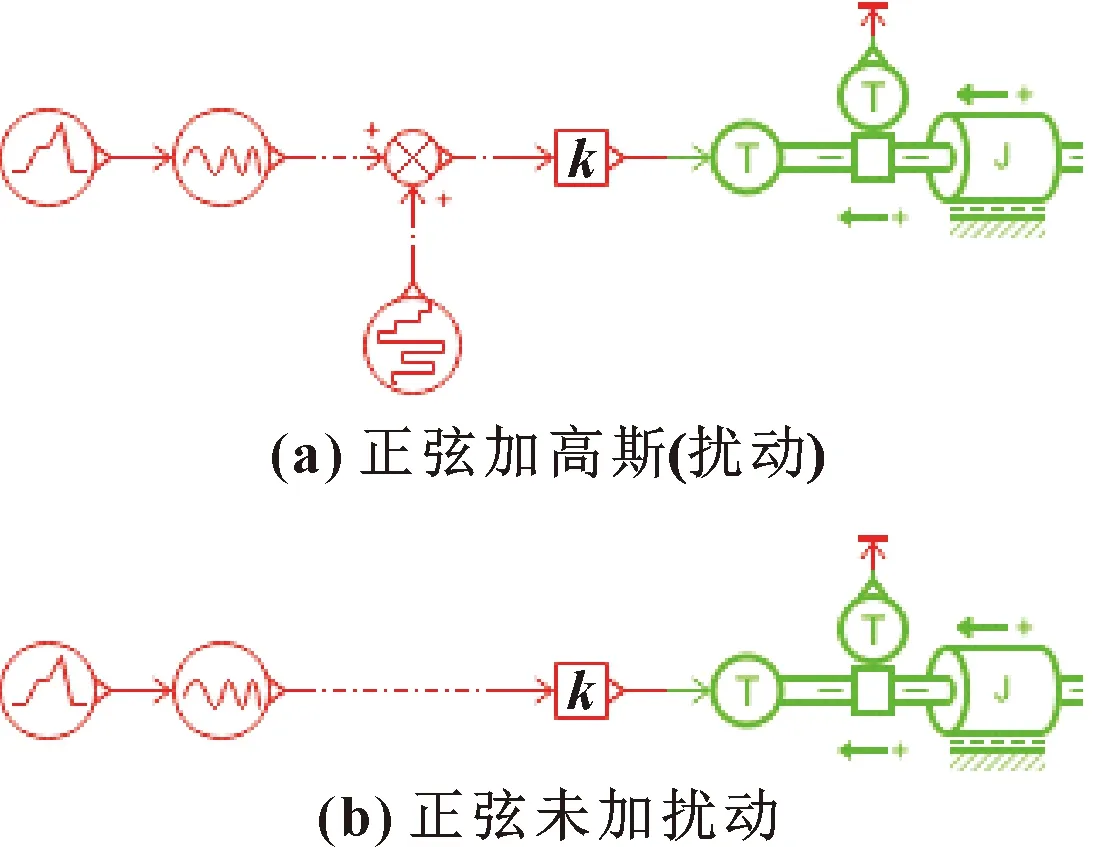
图3 不同模拟负载的仿真模型
仿真时间10 s,采样间隔0.01 s。正弦信号各段的频率由一个分段信号确定,后由增益信号进行处理,增益倍数为2 000,经扭矩转换元件将电信号的无量纲数值转化为扭矩输入到卷筒来模拟负载的干扰。相对于负载受正弦信号控制的回路,受正弦信号加高斯干扰控制的回路仅在负载控制信号部分进行元件更改。
两种干扰信号的形状如图4所示。
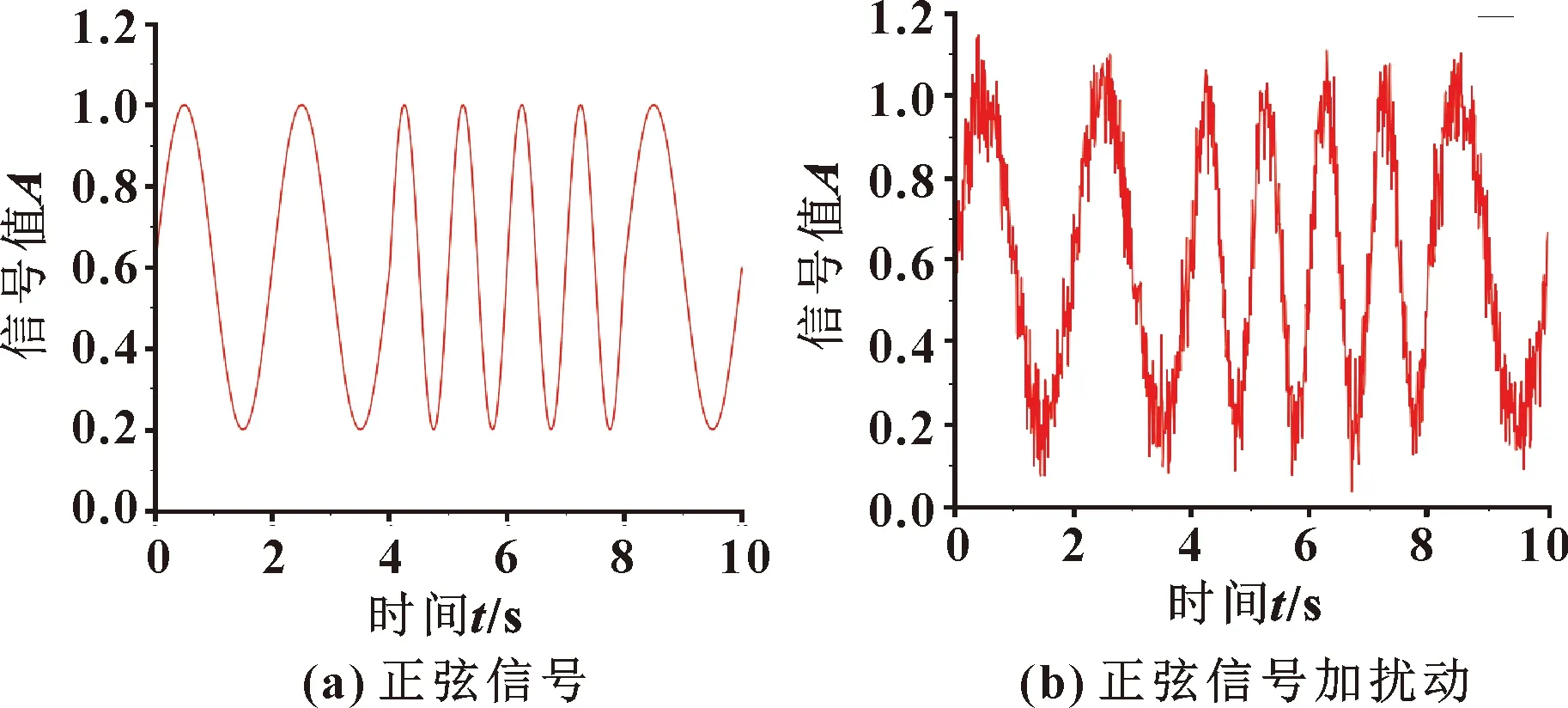
图4 两种干扰信号
仿真结果如图5所示:在正弦信号的控制下,比例阀的进、出阀口压力呈正弦周期性变化。正弦信号未加扰动的压力曲线变化更加光滑,比例阀进、出口压差在到达4×105Pa后由压力补偿阀保持稳定。在补偿阀作用下,当负载的波动引起比例阀出口端压力变化,比例阀入口端压力将跟随出口端压力一起变化,保持稳定的压差,消除了由于负载波动对比例阀控制的影响。
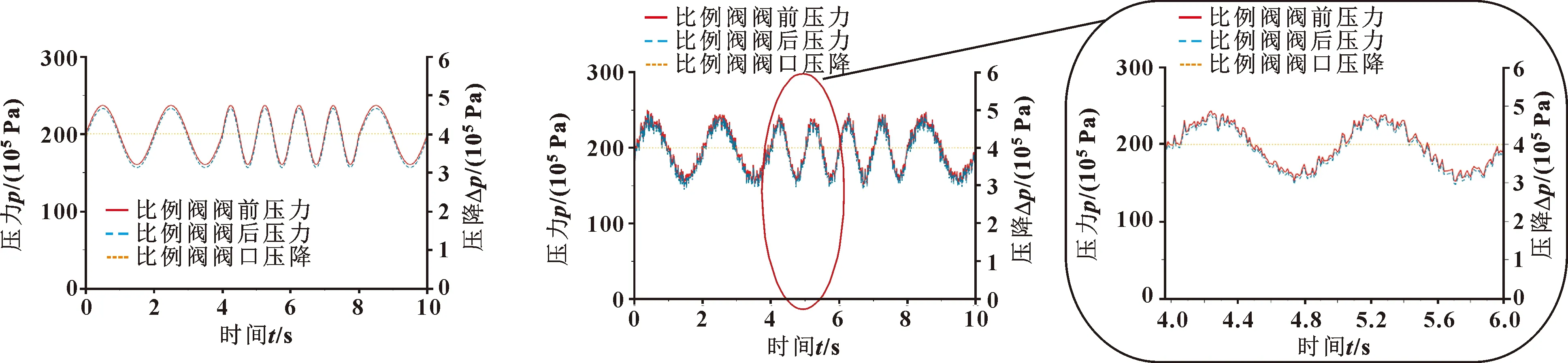
图5 比例阀阀口压力及压降(正弦信号) 图6 比例阀阀口压力及压降(正弦加高斯扰动)
如图6所示:相对于正弦信号未加扰动的仿真结果,正弦信号上的扰动亦反映在比例阀阀口的压力变化上。由此可见,带扰动的正弦信号对比例阀控制的影响更为复杂。即便如此,压力补偿阀依旧很好地维持了阀口的压差,消除了负载波动对控制的影响。
4 变压差压力补偿回路原理分析
这种回路是将定压差压力补偿阀换成变压差压力补偿阀,定压差压力补偿回路中的负载信号直接反馈到压力补偿阀的弹簧腔上。图7所示的变压差压力补偿回路则是将负载的反馈信号经先导元件顺序阀后作用到压力补偿器主阀上。顺序阀在溢流的时候压力p4等于压力p5与弹簧腔所受压力p6之和。即先导型顺序阀会将负载信号放大后再反馈到压力补偿阀,增加幅度为顺序阀的设定压力p6。此时比例换向阀的单边压降便会增加,根据公式(1)可知:在开口一定的情况下,流量随着压差的增加而增加。从而实现比例换向阀在开口不变的条件下调节回路的流量输入。
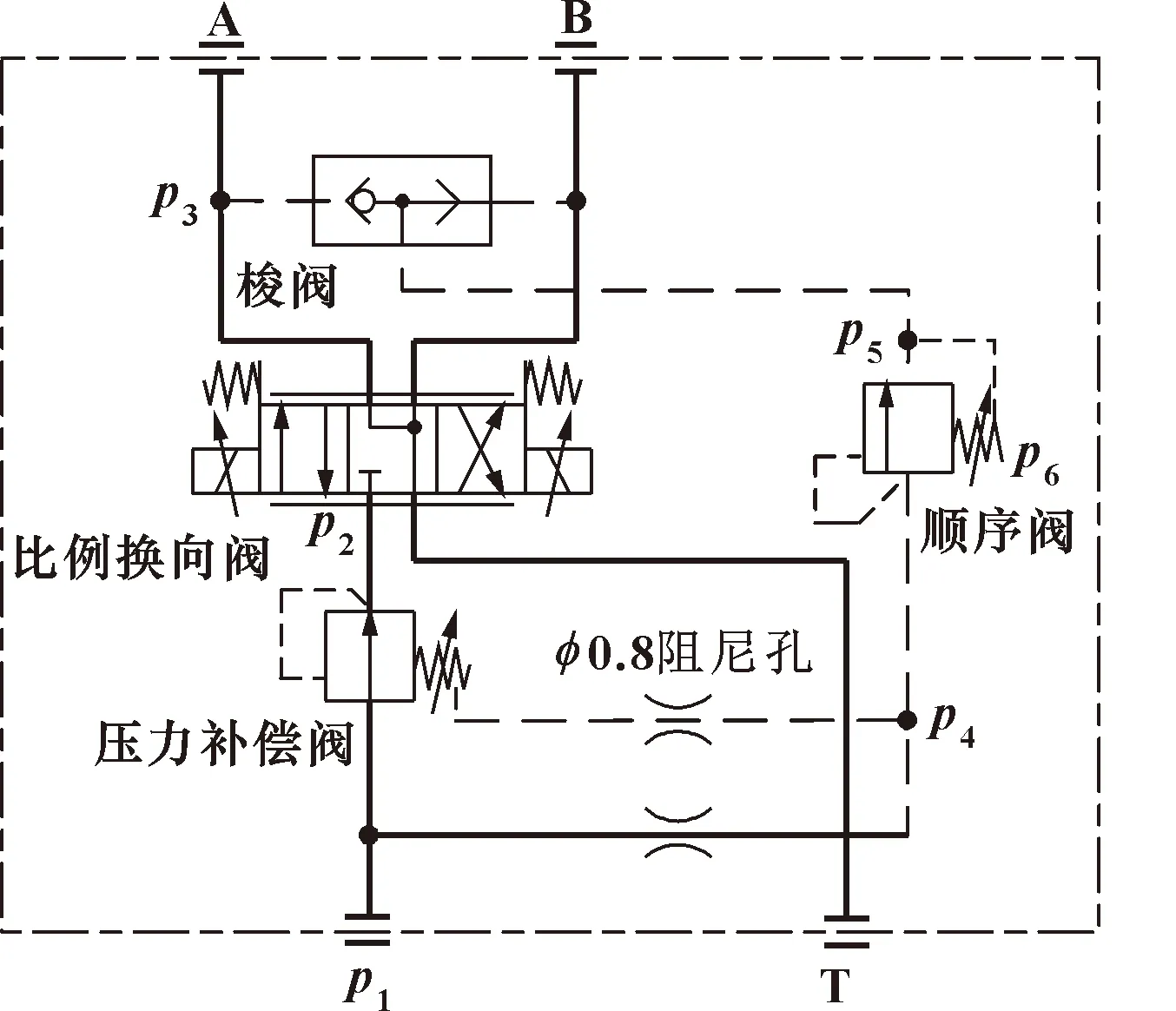
图7 变压差补偿回路原理
5 变压差压力补偿器主阀结构分析
图8所示压力补偿器主阀为常开式结构,阀芯上下作用面积比例为1∶1,通过阀芯的位移来调节通过补偿器主阀的流量。初始时阀芯位于最大开口处,搭配一根软弹簧。主阀与先导元件组合使用,可以通过调整先导元件的设定值来改变比例控制回路中比例阀的压差。
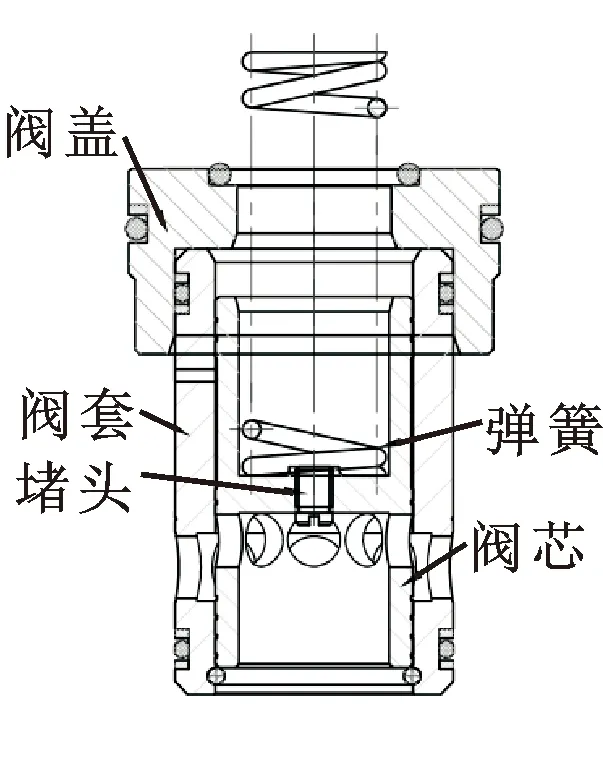
图8 阿托斯SCLI-32374
6 变压差压力补偿回路仿真分析
基于AMESim系统仿真平台搭建的变压差压力补偿回路系统模型如图9所示。
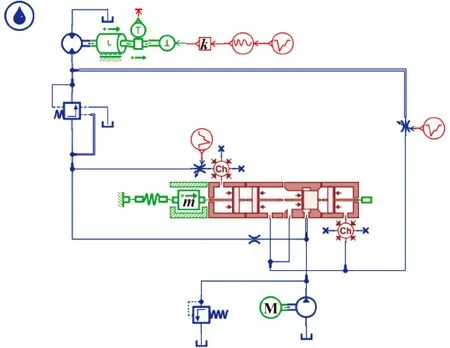
图9 变压差补偿回路仿真模型
变压差补偿回路模型同上述单级压力补偿回路的搭建相似,不同干扰信号控制的回路模型的搭建仅在信号端有所不同。元件参数补充说明见表2。

表2 元件参数补充
区别于单级压力补偿回路中负载压力信号直接反馈到压力补偿阀的弹簧腔,变压差补偿回路的先导元件(顺序阀)将负载信号放大后再反馈到压力补偿器主阀。可以通过改变先导元件的调定压力来改变放大因子,实现比例控制回路的变压差控制。仿真初步设定顺序阀的调定压力为1×105Pa,在正弦信号的控制下,结果如图10所示。该回路中比例阀阀口前后压力变化同单级压力补偿回路的压力变化趋势相同,压差在达到5×105Pa后保持稳定。这表明采用变压差压力补偿阀的比例控制回路同样具备补偿压力的功能。
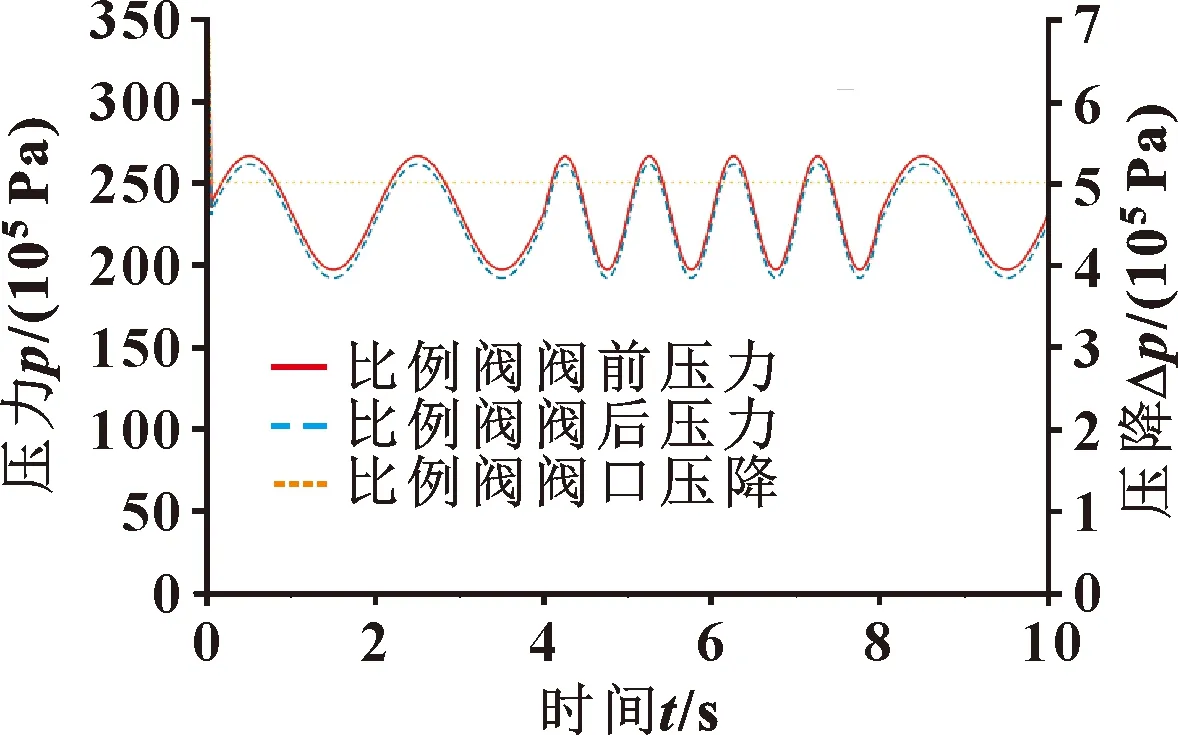
图10 比例阀阀口压力及压降(正弦信号)
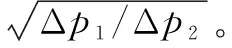
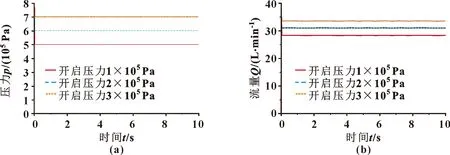
图11 不同调定压力作用下的压差(a)、流量(b)曲线(正弦信号)

重复上述仿真步骤,将未加扰动的正弦信号替换为正弦加高斯(扰动),获得仿真结果如图12所示,信号的扰动亦在比例阀阀口的压力变化上体现出来。
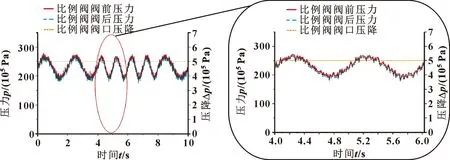
图12 比例阀阀口压力及压降(正弦加高斯扰动)
再次运用AMESim批处理功能,重复上述步骤,获得不同调定压力下的压差、流量曲线如图13所示。

图13 不同调定压力作用下的压差(a)、流量
7 模型验证
由公式(1)可知,在比例换向阀阀口压差一定时,阀口开度与比例控制回路的输出流量成正比。利用仿真以输入信号控制比例阀阀口开度,观察比例阀阀口压差变化,验证模型的正确性。
将节流阀替换为某阀,仿真模型如图14所示。

图14 变压差补偿回路仿真模型(替换节流阀)
根据某阀的流量特性曲线,设置比例阀及输入信号参数见表3。

表3 模型参数补充
比例换向阀在输入信号下的阀口流量及压差如图15所示。仿真模型在阶跃信号的控制下,输出流量与阀口开度成正比关系。在压力补偿阀的作用下,以不同信号连续控制换向阀开口,换向阀单边压降仍能保持稳定,进一步验证了模型的准确性。
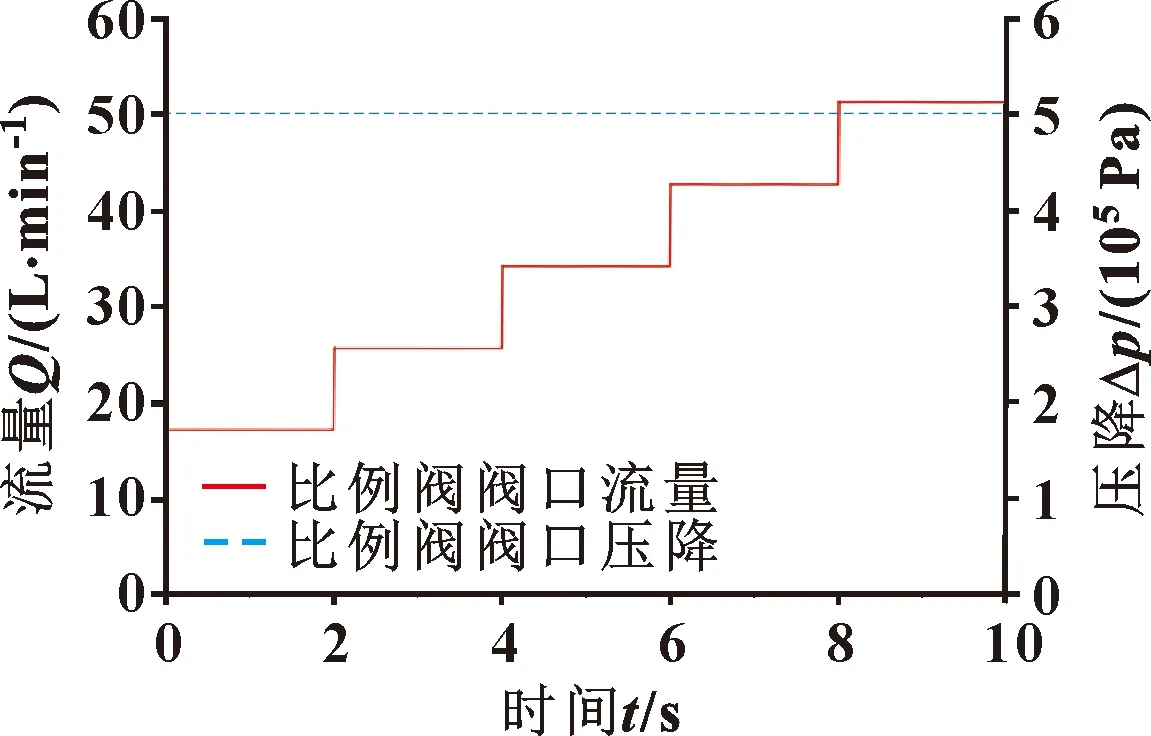
图15 比例阀阀口流量及压降
通过分析上述仿真结果,发现搭建的压力补偿阀能够很好地消除负载波动对比例方向阀控制的影响,验证了仿真模型的准确性,进一步说明了上述仿真分析的可靠性。
8 总结
(1)基于单级、变压差压力补偿回路的原理,在AMESim仿真平台上搭建两种回路的仿真模型。
(2)对单级压力补偿回路仿真模型施加两种不同的扰动信号来模拟回路负载的波动,得到了比例控制回路在不同干扰信号作用下比例阀的压力及压差响应曲线,所得结果符合预期。
(3)对变压差压力补偿回路仿真模型运用相同的处理方式,并且使用批处理功能赋予回路不同的压力补偿值,得到回路在不同补偿值下比例阀的压降及流量响应曲线,同时分析了顺序阀调定压力为1×105Pa时比例阀的压力及压降响应曲线。
分析表明:本文作者分析的一种变压差压力补偿回路在不同的压力调定下,有效消除了负载波动对比例阀控制的影响。通过改变顺序阀设定压力来改变比例阀的压差值,拓宽了回路的速度调节范围,丰富速度调节模式,相比单级调速回路优势明显。
