基于虚拟现实技术的钻具组合运动反演研究*

张 涛 王凯凯 李玉梅 周文彬 邓靖宇

(1.北京信息科技大学 高动态导航技术北京市重点实验室 2.北京信息科技大学 现代测控技术教育部重点实验室 3.中国石油井控应急救援响应中心)

0 引 言

钻井作业是油气开采的重要过程，如何处理好、分析好、利用好钻井过程中的随钻测量数据是安全、高效进行钻井作业的重中之重[1-4]。井下环境复杂，底部钻具组合在作业过程中会受到各种激励作用，产生复杂的振动现象。通过准确的随钻测量数据对井下钻头运动状态进行分析、反演和控制，能够减轻钻头异常振动的危害，提高石油天然气的开采效率。

对于振动数据的位移重建，许自顺等[5]研究了时域积分在振动信号中的应用；王剑等[6]研究了振动加速度数值积分的Lagrange多项式拟合方法，发现在低采样频率下此方法优于辛普森方法；成勋等[7]利用小波去噪的方法对振动数据进行去噪，得到良好的位移重建数据；许晓红等[8]使用组合辛普森的方式对振动的时域积分进行了研究。

对于近钻头的三轴振动数据处理分析，国内外学者进行了大量的研究。A.HOHL等[9-11]对井下高频扭转振动进行了数学建模分析，提出了优化井下钻具组合和钻井操作的建议，以改进钻井性能；CHEN W.等[12]利用深度学习的方法识别底部钻具的工作状态，加快了数据解释的工作效率；E.CAYEUX等[13]根据井下高频数据重建当前测量工具所处位置的三维管道运动，以告知钻井作业团队当前钻头状态；苏晓眉等[14]通过K-Means聚类算法对井下三轴振动数据进行分析，成功实现了对沉砂卡钻的预测；任凯[15]根据跳钻、涡动和黏滑振动的动力学模型和井下三轴振动数据的分析，提出了振动工况的分级和减振措施。

伴随着虚拟现实技术的日渐成熟，虚拟现实技术的高沉浸性、高交互性等优点为数字虚拟井场带来了新的发展。笔者依据随钻测量过程中振动数据的特点，提出一种滑动窗口的积分方法，并建立单自由度振动模型进行分析验证。利用该滑动窗口积分方法将三轴振动数据转换为位移数据，建立虚拟地下钻井场景，利用位移数据和历史数据驱动井下钻头运动，形成了钻头反演运动和数据解释新方式，对虚拟现实井场的完善具有一定的指导意义。

1 加速度积分方法与仿真分析

1.1 时频域积分与滑动窗口积分

加速度、速度和位移是衡量振动强度的3个指标，但由于作业场景的限制，常常不能同时测量这3种参数。为了获得其他参数，一般需要微分或积分操作。井下底部钻具组合的振动由三轴加速度计测得，为了重建钻头的位移，由加速度信号积分得到位移信号是比较可行的方案。

直接时域积分和直接频域积分是2种常用的积分方法，前一种方法是在时间域中通过累积梯形求积公式或者其他求积公式计算：

(1)

式中：a、b是积分区域的上下限；n为将[a，b]等分为多少个间距；f(x)是被积信号。

还有一种积分方法则是先将数据进行频域变换，在频域中进行积分计算，然后再进行反傅里叶变换得到结果[16]，即：

(2)

式中：S(t)是时间段内位移数据信号；wk=2πkFs/N；Fs是采样频率；N是采样数据量；A(k)是加速度信号的频谱；k是非负整数。

根据井下三轴振动信号的特点：随着钻进过程推进，会在不同时间段产生新噪声，即便经过滤波处理也无法完全去除噪声的影响。为了减少其他时间段噪声对当前时间段积分的影响，本文提出一种滑动窗口积分方法：选取合适的窗口大小，在时间域内以相同时间步长滑动，依次对窗口内的加速度信号进行2次频域积分得到该段的位移重建数据。

设a(t)+b1(t)+b2(t)为带噪加速度信号。其中，a(t)为加速度信号，t0到t1窗口内没有噪声；b1(t)为t1到t2窗口的噪声；b2(t)是t2到t3窗口的噪声。则其直接频域积分得到的位移重建信号为：

(3)

滑动窗口积分得到的位移重建信号为：

(4)

式中：A1(k)、A2(k)、A3(k)分别为3个时间段的加速度信号；S1(t)、S2(t)、S3(t)分别为3个时间段的位移重建信号；B1(k)和B2(k)分别为b1(t)与b2(t)的频谱。

对于三轴振动数据来说，直接频域积分需要在整段频域内进行2次积分，会扩大噪声的影响，得到的位移绝对值偏大，而滑动窗口积分则可以在当前窗口内积分，不受窗口外噪声影响，相当于又做了一次滤波，积分过程受噪声影响较小，所以位移值能更好地贴近真实位移。

1.2 积分误差分析指标

为了能够更好地分析滑动窗口积分、时域积分和频域积分的误差情况，引入平均峰值误差、平均最大值误差和均方误差这3个指标[17]。

平均峰值误差可以看出积分信号和实际信号的整体最大峰值和最小峰值的情况：

(5)

式中：A(t)是重建的位移数据；S(t)是实际的位移数据。

平均最大值误差可以看出重建数据和实际数据的局部最大峰值和最小峰值的情况：

(6)

由均方误差可以看出重建数据和实际数据之间偏离的情况：

(7)

1.3 单自由度振动模型

利用Simulink软件建立单自由度振动模型(见图1)，以验证算法的可行性。其中作用力是频率为10 Hz的正弦波信号，施加时间为12 s，模型采样频率为1 000 Hz。使用单位门信号控制噪声的作用时间，从第1 s开始到第12 s每秒加入一个噪声，每次增加5 Hz，频率从10～60 Hz分布。通过传感器模块获取振动模型的加速度、速度、位移数据，并将模拟信号转换成数字信号，同时输出保存加速度、速度、位移数据。

图1 单自由度振动模型Fig.1 Single-degree-of-freedom vibration model

1.4 算法仿真与分析

以单自由度振动模型为基础，仿真时间12 s，采样频率为1 000 Hz，得到120 000个实际加速度和位移采样数据点。

滑动窗口积分相当于以整体时域内的若干段分别代替整体进行傅里叶变换，然后再分别进行频域积分，所以窗口的选择决定了每次积分段内的噪声数量。鉴于窗口太小会导致频谱能量泄露增加，造成积分曲线窗口处不稳定，所以以采样频率为滑动窗口的初始大小L，设定滑动窗口积分的窗口大小分别为iL(i=1，2，3，4，5，6)，确定窗口大小和均方误差的关系，以确定最好的积分效果。同时计算该窗口内主频率幅值和该段窗口总幅值的比，作为窗口大小的依据，得到不同窗口大小下位移重建的均方误差关系曲线，如图2所示。由图2可以发现，当主频率幅值比降低，即当前窗口内的噪声数量增多时，滑动窗口积分的均方误差逐渐增大，滑动窗口积分对实际位移数据的拟合效果在逐步下降。这是由于滑动窗口内的噪声增多，导致正常加速度信号在2次频域积分内的积分区间扩大，造成了其他频率的累积误差，降低了数据拟合的能力。

图2 幅值比与均方误差关系图Fig.2 Relation between amplitude ratio and mean square error

为此，本文取滑动窗口大小为采样频率的大小，对同一段加速度信号进行位移重建积分。对3种积分方法使用同样的积分计算流程：首先对加速度信号进行多项式拟合消除趋势项，一次积分得到速度信号；然后再使用多项式拟合消除一次积分产生的趋势项，二次积分得到位移信号。为了方便结果曲线的观察，分别放大观察1～5 s、5～8 s、8～12 s的曲线，如图3～图5所示。

图3 1～5 s秒位移重建曲线Fig.3 1～5 s displacement reconstruction curve

图4 5～8 s位移重建曲线Fig.4 5～8 s displacement reconstruction curve

从图3～图5可以看出：直接时频域积分都明显受到噪声信号的影响，发生“摆偏”现象，而滑动窗口积分的位移重建相对较好，能够拟合实际位移曲线。

为了量化误差，引入平均峰值误差、平均最大值误差和均方误差这3个指标，得到结果如表1所示。

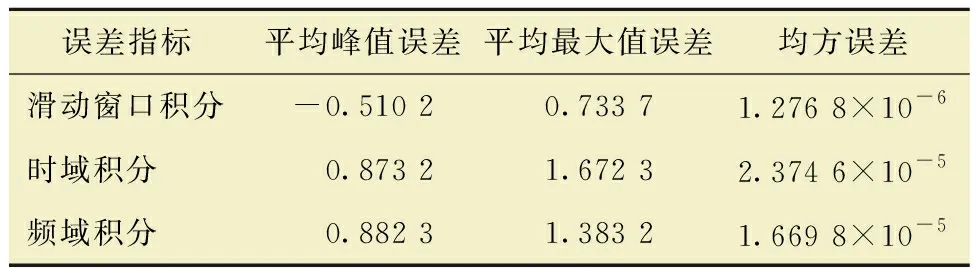
表1 3种积分位移重建误差Table 1 Displacement reconstruction error of 3 kinds of integrations

由于多个噪声的存在，即便做了趋势项消除，也无法完全根除积分期间产生的非线性趋势项的影响，这使直接时域积分重建的位移数据发生“摆偏”。对于直接频域积分来说，不进行频率截断，即不将主频率之外的频率置零处理，直接频域积分会受到频率相近噪声的影响，和时域积分一样产生“摆偏”。由于计算值和实际值的差值过大，部分区域误差达到几毫米，所以导致时频域的平均最大值误差非常大。

而滑动窗口积分的各个窗口之间的积分过程相对独立，对每个积分窗口来说相当于做了频率截断处理，降低了当前积分窗口内的噪声数量，因而能够相对较好地拟合实际的位移信号。由均方误差也可以看出，直接时频域积分的均方误差是滑动窗口积分的20倍左右。这充分证明了滑动窗口积分运用于振动位移重建的可行性。但是由于矩形窗口的加入会导致频谱能量泄露，所以滑动窗口积分在滑动窗口交界处和实际位移信号相似度较小。

2 钻头运动的反演可视化研究

2.1 井下测量数据的处理

本文采用的三轴振动数据为新疆某油田钻井过程中的实测数据，数据测量点在近钻头测量短节。该测量数据记录了井下钻具组合在钻井过程中的钻速、钻压、扭矩和三轴加速度数据，信号采样频率为400 Hz。

为了重建底部钻具组合的振动位移信号，首先对井下测量的三轴振动电压数据进行数据的预处理操作，以得到加速度数据；然后对三轴加速度数据以采样频率为窗口大小分别进行2次滑动窗口积分得到位移数据，如图6所示。从图6可以发现，滑动窗口积分较好地由振动加速度数据恢复了振动的位移数据，位移数据大致在毫米级波动，处于正常钻进过程。

图6 三轴位移重建Fig.6 Triaxial displacement reconstruction

2.2 地下虚拟场景的建立与钻具运动反演

为了完整与友好地展示底部钻具组合的运动状态，建立基于虚拟现实技术的地下钻井场景。该地下钻井场景与虚拟井场中的钻井平台联动，属于地下演示模块。

首先，需要明确的是地下钻井场景中法向、切向和轴向振动的正方向。以底部钻具组合模型的前后方向为法向振动方向，其中正方向向前；以底部钻具组合模型的左右方向为切向振动方向，其中正方向向右；以底部钻具组合模型的上下方向为轴向振动方向，其中正方向向下。三轴振动正方向如图7所示。

图7 三轴振动正方向Fig.7 Positive direction of triaxial vibration

其次，虚拟地下钻井场景应当包含以下几个模块：数据流展示模块、底部钻具组合演示模块、地层模块及用户交互模块。

数据流展示模块：以实际数据为基础，通过实时动态折线图的方式进行钻井过程中实测的钻速、三轴振动等信号的数据回放。为了实现折线图的动态移动方式，以相同的时间帧传入数据流，将数据归一化处理，并依次绘制数据，实现旧数据的移除与新数据的注入，从而实现动态折线图的更新绘制。

底部钻具组合演示模块：以实际振动数据为基础，选取底部钻具组合模型的本地坐标中心为振动中心，根据三轴振动数据重建的三维位移数据实时驱动模型的振动，反演钻具组合的中心偏移情况；以实际钻速数据驱动钻具组合的转动速度。同时，考虑到虚拟地下场景运行环境的显示稳定性和运行设备的性能，将底部钻具组合的驱动频率设为200帧，即在虚拟地下场景中每2 s才能运行完1 s实际数据。图8为底部钻具组合模型。

图8 底部钻具组合模型Fig.8 Bottomhole assembly model

地层模块：为了减少地层空间建模体积，提高虚拟钻井场景的性能，通过地层向上移动的方式反衬钻头钻进的过程。构建动态地层着色程序(shader)，根据钻速大小改变地层上移速度，钻速快，地层上移快，钻速降低，降低地层上移速度，以动态模拟底部钻具组合钻进的画面，优化视觉效果。图9是地层空间的俯视图。

图9 地层空间俯视图Fig.9 Top view of formation space

用户交互模块：用户通过虚拟手柄选择是否启动底部钻具组合运动反演。选择是，则暂时切断地下钻井场景与地上钻井平台的联动，转换为钻头运动反演情景，确保虚拟地下环境的运行效率。

地下钻井场景的虚拟场景如图10所示。图10中：中间是底部钻具组合模型，实时通过实际数据驱动钻具组合的运动反演；左右两边的UI是实际数据流折线图，左边依次是法向振动加速度和切向振动加速度，右边依次是轴向振动加速度和钻速，展现当前历史数据的大小。

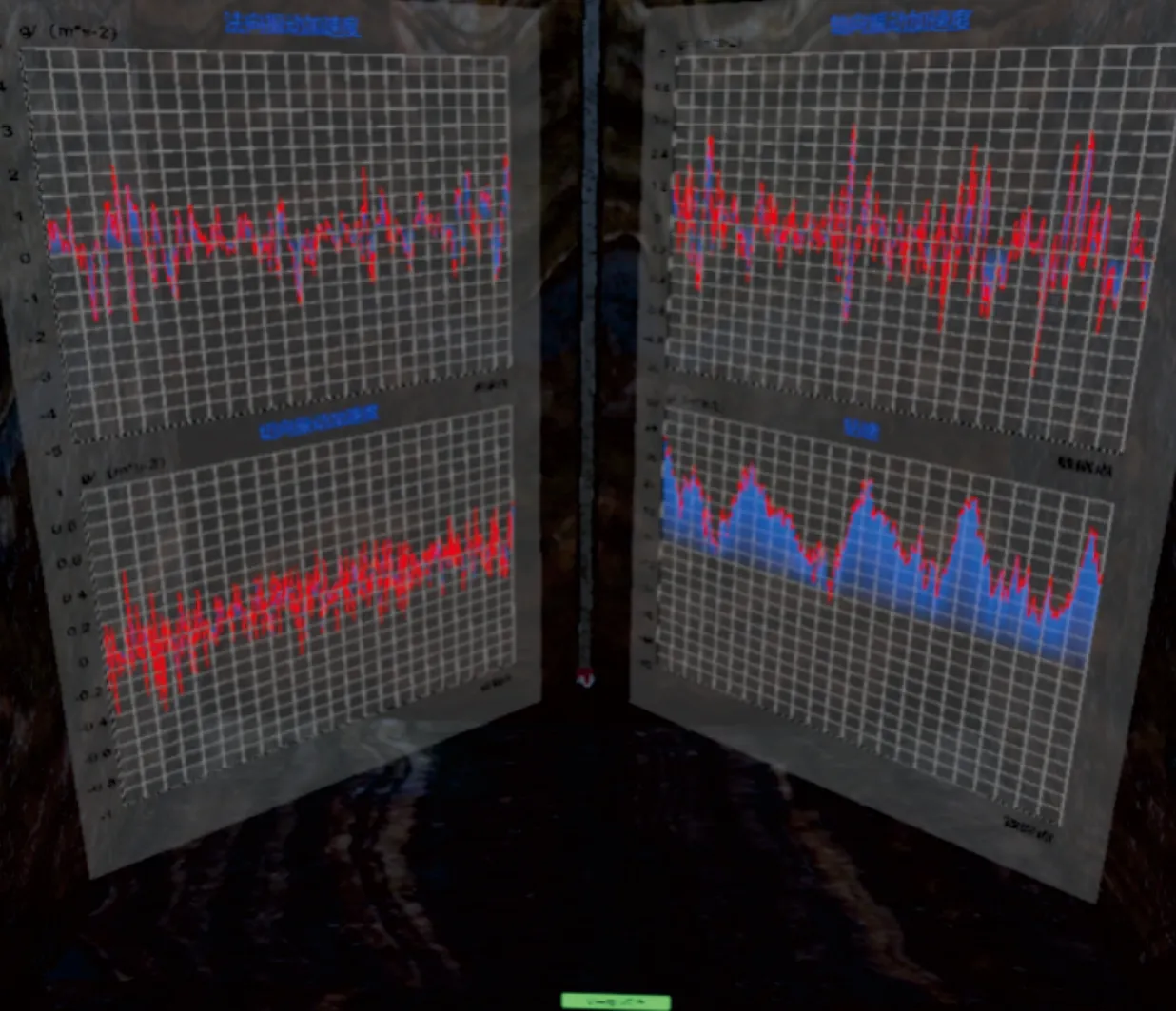
图10 虚拟地下钻井场景Fig.10 Virtual underground drilling scene

基于以上工作，本文建立了基于虚拟现实技术的底部钻具的运动反演场景，用户可以佩戴虚拟现实设备进入地下钻井场景，通过相应的手柄交互，实现底部钻具组合的运动反演观测。

3 结 论

本文针对振动数据滤波后仍存在噪声干扰的问题，提出滑动窗口积分的位移重建方法，首先建立单自由度振动模型进行算法的验证；然后将滑动窗口积分方法用于井下振动数据的位移重建，建立了基于虚拟现实技术的底部钻具组合的运动反演观测场景，用户可以通过虚拟现实设备进入场景。研究结果表明：

(1)通过原理分析与仿真对比的研究手段可以发现，直接时频域积分在加速度信号的积分过程中受噪声干扰较大，而本文提出的滑动窗口积分相当于在直接频域积分的基础上做了一次频率截断，降低了当前窗口内的噪声数量，能够更好地拟合实际位移曲线。

(2)利用滑动窗口积分的方法对井下振动信号进行位移重建，构建基于虚拟现实技术的地下钻井场景，根据钻速数据和位移数据驱动底部钻具组合运动反演，利用虚拟现实设备即可进行运动观测和数据分析。表明了通过实际钻井数据重现钻井过程的可行性，拓展了虚拟现实技术在石油钻井井场的应用范围。