基于Johnson-Cook模型的剪切闸板性能仿真*
2023-07-22曹银萍康钊飞李国亮窦益华孙祥鑫陈泽田
曹银萍 康钊飞 李国亮 窦益华 孙祥鑫 郑 杰 陈泽田
(1.西安石油大学机械工程学院 2.中国石油西部钻探试油公司)
0 引 言
在钻井过程中防止重大事故的发生是安全生产的头等大事。井喷是钻井过程中常见的重大事故之一,危害性大,轻则造成井的报废,重则造成一定范围内油井的停产和人员伤亡[1]。剪切闸板作为应对井喷事故的核心部件之一,其关键在于如何高速有效剪断连续管并且实现封井。
目前,国内外学者提出了众多关于剪切闸板性能及连续管研究的方法。韩传军等[2]对ISR剪切闸板进行性能评价并且以试验为基础,认为ISR型剪切闸板的最优结构参数是倒角45°、V形夹角163°、刀面倾角1°或2°。李明飞等[3]以油田常用P110S管材为研究对象,获得以Johnson-Cook为代表的材料动态本构模型关键参数,提高动载作用下管柱强度安全分析精度。曹银萍等[4]利用材料力学理论,以4种规格水平套管为例,对比分析考虑扁化效应下套管的抗外挤强度。蔚海文[5]认为钻杆带压剪切技术为处理井喷事故提供了新的方案。陈浩等[6]认为剪切力随着钻杆长度的增加而呈下降趋势。刘冰等[7]建立了剪切闸板防喷器剪切钻杆断口几何形状模态方程,并进行了数值模拟与剪切试验,得到剪切性能最优的V形夹角。TANG Y.等[8]通过有限元软件与静压水测试试验,得到了剪切闸板防喷器壳体的主要应力集中区域。A.TEKIN等[9]通过数值计算与有限元仿真分析,得到优化的闸板几何形状以减小剪切力;A.TEKIN[10]又对防喷器闸板倒角夹角对剪切管柱的影响提出分析。LIU Z.G.等[11]通过对钻柱切断后的形状判断来分析剪切闸板的力学性能。刘冰等[12]综合考虑剪切闸板结构及作业参数,运用楔形应力理论,建立了相应阶段的闸板刃口应力求解模型。王旭东等[13]以压应力公式作为理论基础,建立了预测模型,有效弥补了对剪切闸板剪切能力预测评估的不足。
上述研究对剪切闸板性能分析有着重要作用,但多集中于闸板应力分析及钻杆参数分析,而对连续管规格、剪切闸板刃口夹角对剪切力的影响研究还不够系统和深入。为此,本文在上述研究的基础上,以Johnson-Cook模型为基础,建立了剪切闸板剪切连续管有限元模型,对剪切连续管过程中的剪切应力进行了分析,同时分析了连续管壁厚、长度及剪切闸板V形夹角等参数对剪切应力的影响规律。所得结论对连续管剪切闸板结构设计及连续管剪切性能分析可提供参考。
1 剪切闸板剪切连续管模型分析
1.1 剪切连续管过程分析
闸板剪切连续管时,连续管的运动可分为3个阶段:剪切闸板靠近并接触连续管;剪切闸板开始挤压连续管,使连续管屈服,刀刃插入连续管;连续管被剪切闸板挤压断裂,完成剪切[14]。剪切闸板剪切连续管模型如图1所示。以RP-1和RP-2为约束启动点向剪切闸板中心移动,以刀刃冲击块刀尖A点为切入点冲击连续管,A1、A2、A3分别为接触点、挤压点、断裂点。剪切运动过程如图2所示。

图1 剪切闸板剪切连续管模型Fig.1 Model of coiled tubing shorn by shear ram

图2 剪切点切入连续管Fig.2 Cutting into coiled tubing at shear point
1.2 剪切连续管过程剪切应力分析
剪切闸板剪切连续管是通过巨大的推力压裂连续管,使连续管产生塑性变形,最终剪断连续管,其中剪切刀刃切入连续管至最终切断连续管的应力变化趋势一直是剪切闸板不可忽视的一点[15-18]。剪切闸板在进行剪切作业时,上、下闸板相对连续管截面错动。假设剪切过程中剪切应力在剪切面内分布均匀,即剪切应力大于剪切连续管材料的剪切屈服应力时,连续管开始发生剪切破坏,可表示为[19]:
(1)
式中:τ为连续管所受剪切应力,MPa;F为剪切闸板提供的剪切力,N;S为连续管截面积,mm2;[τm]为连续管材料的剪切屈服应力,MPa。
根据Von Mises屈服准则,切断连续管所需剪切力计算式为:
(2)
式中:σs为材料屈服极限,MPa;R为连续管外半径,mm;r为连续管内半径,mm。
1.3 本构模型选择
本构模型反映了材料在加工变形时应力与位移、应变率、温度之间的关系,也是确保仿真结果正确和可靠的基础[20]。本构模型采用Johnson-Cook模型,可表示为:
(3)

在模型参数中,材料初始屈服应力A不应过大,取1 016 MPa,应变强化系数B取0.65,C取0.07,ε取1,T*取常温25 ℃。
1.4 断裂损伤模型选择
断裂损伤原则用来预测损伤萌发情况和断口质量。常用的断裂准则有柔性损伤、Johnson-Cook和Shear Damage原则。前2种参数难以获取,本文采用Shear Damage模型,该模型在预测剪切接触、挤压及剪断等方面具有较好的动态特性,同时具有良好的展示效果,并且可以显示高速剪切[21],公式可表示为:

(4)
式中:Csf为断裂临界判断值,当Csf=1时产生断裂;ε0为初始等效塑性应变;Δγ为等效塑性应变增量;εf为断裂时等效塑性应变。
2 剪切连续管有限元模型建立
连续管网格单元采用六面体单元C3D8R,单元格为10 290。为缩短运行时间,剪切闸板采用四面体单元C3D4进行网格划分,单元格为43 541。剪切闸板剪切连续管网格模型如图3所示。

图3 剪切闸板剪切连续管网格模型Fig.3 Grid model of coiled tubing shorn by shear ram
剪切过程的有限元模拟是将剪切闸板和连续管的几何形态建立出来,进行材料定义,并且划分网格,进而进行仿真分析。表1为仿真所采用的材料参数。

表1 材料力学性能参数Table 1 Mechanical properties of materials
剪切闸板剪切连续管时连续管应力云图如图4所示。

图4 连续管应力云图Fig.4 Cloud chart for stress of coiled tubing
连续管依次发生弹塑性变形、裂纹萌生、裂纹扩展及断裂分离。图4a为剪切闸板刚接触连续管,应力为127.3 MPa。图4b为连续管开始萌生裂纹,此时连续管被挤压部分开始发生变形。随着剪切闸板的不断深入,连续管裂纹开始不断扩展,应力开始集中,如图4c所示。剪切闸板合拢后将连续管剪断,断口形状如图4d所示。
图5为剪切应力随位移的变化拆线图。由图5可以看出,AB段、BC段及CD段分别对应连续管刚接触被挤压、连续管产生塑性变形、连续管被剪断段。在16 mm处和26 mm处产生2次峰值,第一次是因为裂纹底部已经被挤压完全,开始向上部产生裂纹,所以应力产生回落。第二次是因为上部裂纹产生完全,连续管被断裂。
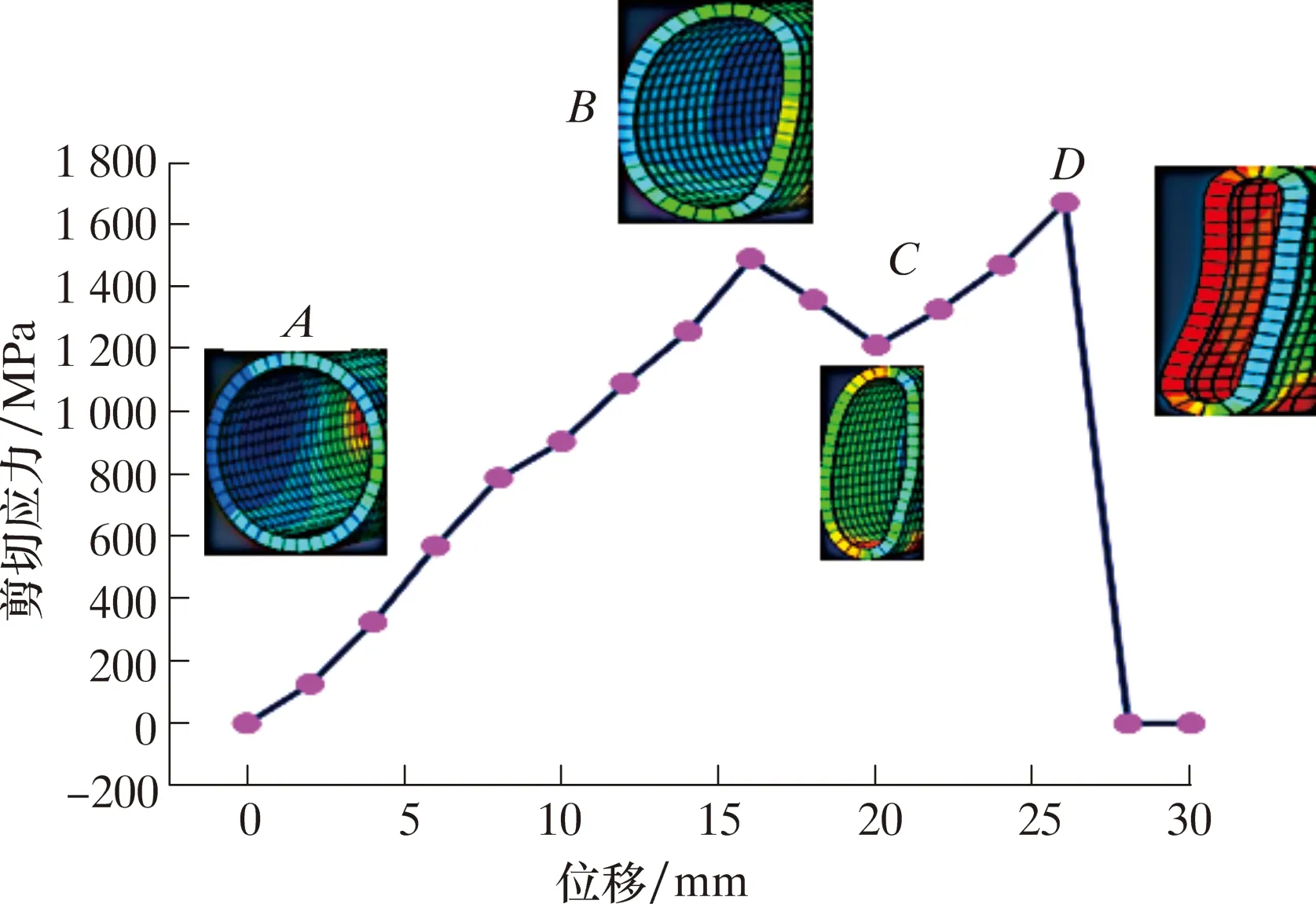
图5 剪切应力随位移变化折线图Fig.5 Variation of shear stress with displacement
3 剪切连续管过程因素分析
闸板剪切连续管过程中,剪切闸板和连续管的众多参数都会影响剪切闸板的剪切性能,比如V形刃口夹角、连续管的长度和壁厚等。合理分析这些参数可以为剪切闸板工作提供一定的参考,也会使剪切闸板工作更加高效,延长剪切闸板使用寿命[22]。
3.1 连续管壁厚对剪切性能的影响
不同的连续管壁厚会有不同的剪切要求和剪切效果,连续管管壁过薄,就会使截面积过大,管壁过厚,剪切闸板需要克服的阻力也就会增大。因此,分析不同壁厚对剪切闸板的剪切效果影响有一定的参考价值。图6为ø38.1mm连续管不同壁厚时剪切力变化曲线。

图6 不同壁厚连续管剪力变化曲线Fig.6 Variation of shearing force of coiled tubing with different wall thicknesses
随着连续管的壁厚不断增加,剪切力峰值在不断的增加,呈现出单一上升的趋势,在壁厚为2.591和2.796 mm时,剪切力峰值相差不大,相差在50 kN左右。壁厚为3.404和3.175 mm时,剪切力峰值仅相差不到200 kN。
剪切闸板在剪切不同壁厚连续管时,剪切应力整体随着连续管的壁厚增加而增加,壁厚越小,剪切闸板剪切应力差距越小,同时,应力峰值差值也较小,如图7所示。用ABAQUS软件进行仿真,将仿真数据与剪切应力公式(式(1))计算数据进行比较,结果如图8所示。

图7 剪切不同壁厚连续管时上、下闸板剪切应力曲线Fig.7 Shear stress curves of upper and lower rams when cutting coiled tubing with different wall thicknesses

图8 公式计算结果与仿真结果对比曲线Fig.8 Comparison curve of formula calculation results and simulation results
由图8可知,随着连续管的壁厚不断增加,连续管剪切应力峰值总体上升,采用剪切应力公式计算比较保守。壁厚不断增加,误差值越来越大,主要有以下因素:①剪切应力公式没有考虑剪切闸板对连续管的摩擦力;②仿真软件充分考虑工况,比如井压和损伤准则等;③公式没有考虑V形夹角对于连续管剪切的影响。
3.2 连续管长度对剪切性能的影响
连续管越长其自重越大,连续管越短其自重越小[23]。连续管在自重的作用下受拉。为了模拟下端钻柱重力,将下端钻柱重力转换为集中载荷施加在连续管模型下面。连续管长度对应的载荷及自重如表2所示。

表2 ø38.1 mm CT90连续管自重对应的集中载荷Table 2 Point load corresponding to deadweight of ø38.1 mm CT 90 coiled tubing
连续管在自重作用下,长度越长,受拉的作用也越来越明显。模拟连续管下端重力,将下端重力转换为集中载荷施加到连续管模型下端面。图9是连续管长度为2 000、3 000、4 000和5 000 m时闸板剪切应力随长度的变化曲线。
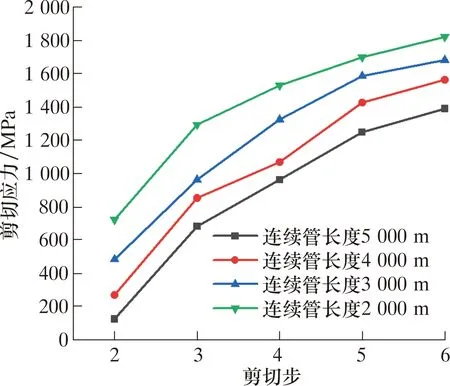
图9 剪切应力随连续管长度的变化曲线Fig.9 Variation of shear stress with length of coiled tubing
在塑性变形之前,连续管处于弹性形变阶段,剪切应力变化趋势较大;当应力峰值大于材料的屈服强度时,连续管产生塑性变形,直到连续管被剪断,此时即使连续管长度在不断增加,但是剪切应力已经趋于平缓,变化速率已经下降。从图10可以看出,随着连续管的长度不断增加,剪切应力却在不断减小,不同长度连续管的加载载荷不一样,但是应力变化趋势一样。
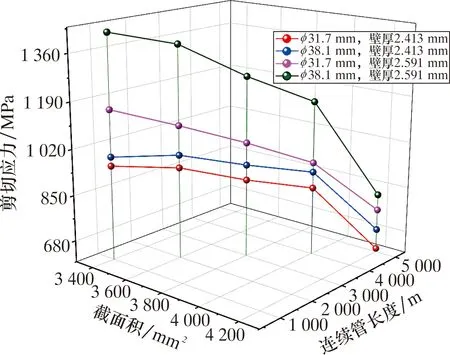
图10 剪切应力随截面积与长度变化折线Fig.10 Variation of shear stress with sectional area and length
随着连续管的长度不断增加,剪切应力整体是下降趋势,连续管长度小于3 000 m时,剪切应力趋势较为平缓,在此过程中,连续管所受的自重对剪切影响较小;连续管长度在3 000 m以上时,其自重起主要作用,导致剪切应力力大幅度下降。
3.3 剪切闸板V形夹角对剪切性能的影响
剪切闸板V形夹角的变化对连续管的剪断有着重要影响[22]。随着V形夹角的减小,闸板应力区域范围不断缩小,上闸板应力范围在786~1 564 MPa之间,下闸板应力范围在952~1 489 MPa之间,如图11所示,V形夹角在158°左右应力峰值相对较低。剪切闸板V形夹角不同时剪切闸板应力如表3所示。

表3 不同V形夹角下剪切应力计算结果Table 3 Calculation results of shear stress at different V-shaped angles
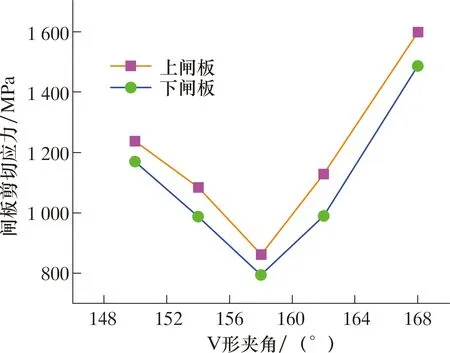
图11 不同V形夹角下剪切应力曲线Fig.11 Shear stress curve at different V-shaped angles
4 结 论
(1)随着连续管壁厚的不断增加,剪切力峰值总体呈上升趋势,在塑性变形阶段之前,剪切力平缓上升,塑性变形之后,上升幅度较大。不同壁厚的连续管剪切应力峰值相差在200 kN,应根据不同的工况选取不同壁厚的连续管。
(2)随着连续管长度的不断增加,其剪切应力在不断减小,3 000 m以上连续管,剪切应力明显下降,主要原因是下端拉力在剪切作业中起到了主导作用,进行连续管剪切作业时,连续管越长越有利于剪切。
(3)随着剪切闸板V形夹角的增加,剪切应力先减小后增大,V形角在158°时,上、下闸板应力最小,剪切性能最优。
