基于ABAQUS的温度对钻井液漏失影响规律*

2023-07-22冯永存古臣旺邓金根

石油机械 2023年7期

张帅冯永存古臣旺邓金根

(中国石油大学(北京)石油工程学院)

0 引言

我国深层油气资源量大、分布广，开采前景广阔。但高温、高压、高应力的地层特点导致钻井过程中井漏事故频发，严重制约了勘探开发进度。

漏失裂缝尺寸是指导堵漏工艺选择和堵漏材料优化的关键依据。裂缝尺寸预测不准会导致堵漏材料尺寸与裂缝入口尺寸不匹配，难以有效封堵或堵漏颗粒在入口处封门[1]。尽管利用测井资料、地震资料以及成像测井等手段可以直接或间接获得井壁上的裂缝尺寸，但存在精度低、价格昂贵以及仅能提供缝口尺寸等缺点[2-3]。目前，国内外主要通过推导解析解和数值模拟来预测漏失裂缝尺寸。

漏失裂缝解析解主要借鉴水力压裂相关研究成果。2004年，M.W.ALBERTY等[4]首先在其经典的“应力笼(Stress Cage)”论文中，提出了线裂纹解析模型计算单一漏失裂缝尺寸的方法。该模型简洁易用，国内外多数堵漏软件均采用了该模型，但前提是在直井、均匀应力和均匀缝内压力分布的理想状态下才成立。此后，国内外学者在此基础上逐渐考虑了井斜、应力各向异性、非均匀缝内压力分布、多裂缝等因素影响的漏失裂缝尺寸和漏失压力相关的解析模型[5-10]。然而这些模型均基于线弹性假设，并大多忽略了井周应力集中、井筒-裂缝-地层之间的传质、传热等因素对裂缝尺寸的影响。

为获得更加准确的裂缝尺寸预测结果，很多学者采用数值模拟方法。如WANG H.M.等[11-12]基于线弹性假设，分别用边界元和有限元的方法建立了漏失裂缝模型，考虑了井周应力集中对裂缝尺寸的影响，但未考虑渗流和传热的影响。曾义金等[13]也利用类似的有限元模型对井周裂缝宽度进行了预测。为了进一步探究井筒-裂缝-地层之间的渗流对漏失裂缝的影响，FENG Y.C.等[14-15]基于孔隙弹性假设，建立了漏失裂缝的有限元模型。为了研究动态漏失裂缝尺寸，S.SALEHI[16]利用水力压裂研究中常用的内聚力单元法对漏失裂缝的扩展进行了模拟，但其模型直接套用水力压裂模型中恒定注入速率边界条件，与动态裂缝尺寸实际情况不相符，因此无法正确解释漏失裂缝在钻井循环过程中的动态漏失和扩展规律。为解决该问题，FENG Y.C.等[17]基于ABAQUS有限元平台，建立了“井筒循环-裂缝扩展-岩石变形”一体化漏失预测模型。该模型考虑了井筒内钻井液循环对裂缝生长的影响，同时考虑了钻井液向裂缝内漏失对井筒循环的影响，从而更加准确地描述了漏失裂缝的扩展情况。然而，“井筒-裂缝-地层”之间的传热对漏失裂缝尺寸的影响尚未见相关报道。

综上所述，近年来漏失裂缝尺寸预测模型有了很大进展。但现有模型都无法预测钻井波动压力、温度影响下漏失裂缝尺寸的动态变化规律。

为此，笔者提出一种钻井动态循环“热-流-固”全耦合模型，通过井筒和地层之间的耦合，实现钻井过程中考虑温度影响的动态井底压力和漏失裂缝的模拟。模型通过ABAQUS软件，利用耦合温度的管流单元、孔隙压力单元和内聚单元，分别实现井筒循环、地层位移-孔压-温度变化以及裂缝起裂和扩展的全耦合模拟。应用该模型开展了高温地层中钻井液温度对漏失规律影响的研究。

1 概念模型

钻井液漏失模型如图1所示。

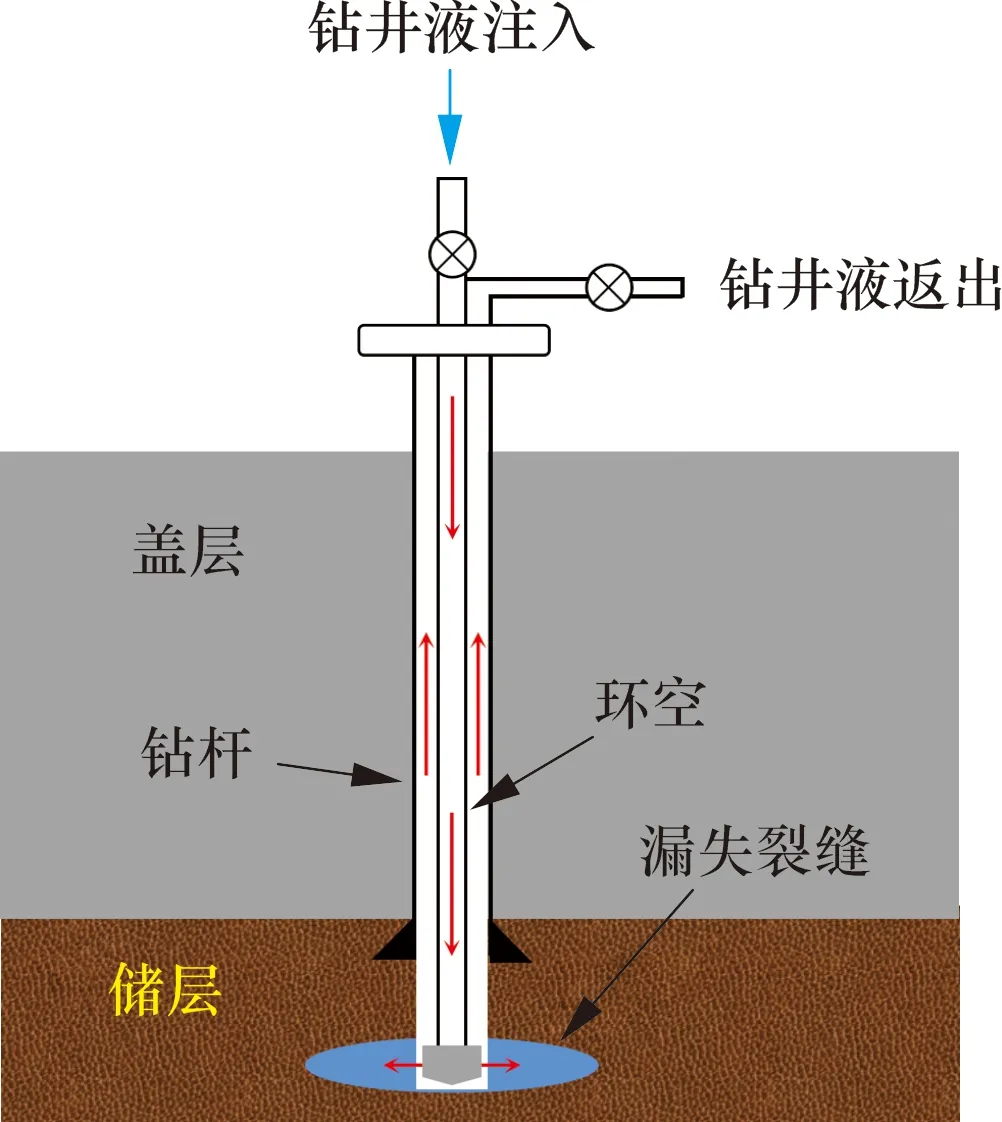
图1 钻井液漏失模型示意图Fig.1 Schematic diagram of drilling fluid loss model

据统计，超70%的漏失为裂缝性漏失，其中又以压裂性漏失为主[18-19]。钻井循环过程中，当井筒内压力超过地层破裂压力时，裂缝开启，钻井液漏失。本文利用ABAQUS平台建立“井筒-地层-裂缝”耦合模型，研究钻井液温度对漏失规律的影响。

模型包括井筒、地层和裂缝，分别采用管流单元、孔隙压力单元和内聚力单元进行建模。模拟过程为：钻井液沿井口泵入钻杆，从环空返出，实现循环。期间如果发生漏失，钻井液将沿着裂缝进入地层，改变地层的应力场和温度场。

2 基础理论

2.1 管流模型理论

以管流单元表征井筒和环空，模拟钻井液的循环。假设流体单相不可压缩，基于伯努利方程计算管内流体在流动过程中的黏度、重力和压力损失。单元中两点之间的流动方程如下[20]：

(1)

式中：Δp为两节点间的压力差值，Pa；ΔZ为两节点之间的海拔高度差值，m；ρ为管内流体的密度，kg/m3；g为重力加速度，m/s2；CL为损失系数；Ki为定向损失系数；v为流体的流动速度，m/s；

2.2 热-流-固耦合理论

热-流-固耦合模型(见图2)可同时考虑流体渗流、岩石变形和温度变化等因素。流体渗流改变岩石孔隙压力和有效应力，导致孔隙和裂缝变形；渗流伴随着流体和地层之间的热量交换，引起温度场的变化，产生热应力，进一步影响岩石的变形[21- 22]。

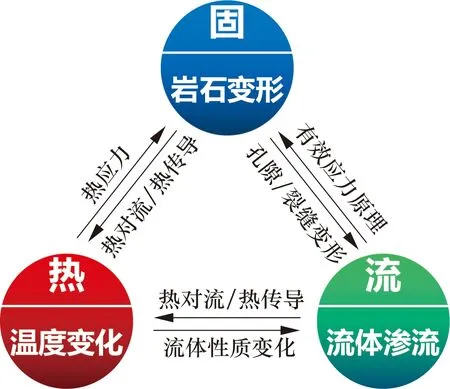
图2 热-流-固耦合相互作用示意图Fig.2 Schematic diagram of thermo-hydro-mechanical coupling interaction

根据虚功原理，岩石骨架的平衡方程为[23]：

(2)

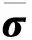
岩石内部渗流控制方程为[23]：

(3)

式中：J为多孔介质体积变化率；ρw为流体密度，kg/m3；nw为孔隙比；vw为流体渗流速度，m/s；x为空间向量，m。

考虑热孔隙弹性的岩石本构方程为[24]：

(4)

其中：

(5)

式中：σij为总应力张量，Pa；εij为总应变张量；εkk为静止压力应变张量；G、λ为拉梅常数，Pa；γ为热膨胀系数，℃-1；ΔT为温度变化量，℃；E为弹性模量，Pa；μ为泊松比；α为biot系数；δij为1(i=j时)或0(i≠j时)，无量纲。

2.3 裂缝区损伤模型

以Cohesive单元表征裂缝起裂和延伸，以牵引-分离定律作为裂缝起裂准则。牵引分离定律损伤准则如图3所示。起裂包括损伤起始和损伤演化2个阶段。裂缝初始是闭合且完好无损的，在外部载荷的作用下，Cohesive单元开始出现刚度退化，当外载荷达到抗拉强度时，开始起裂，直到完全失效，形成裂缝。

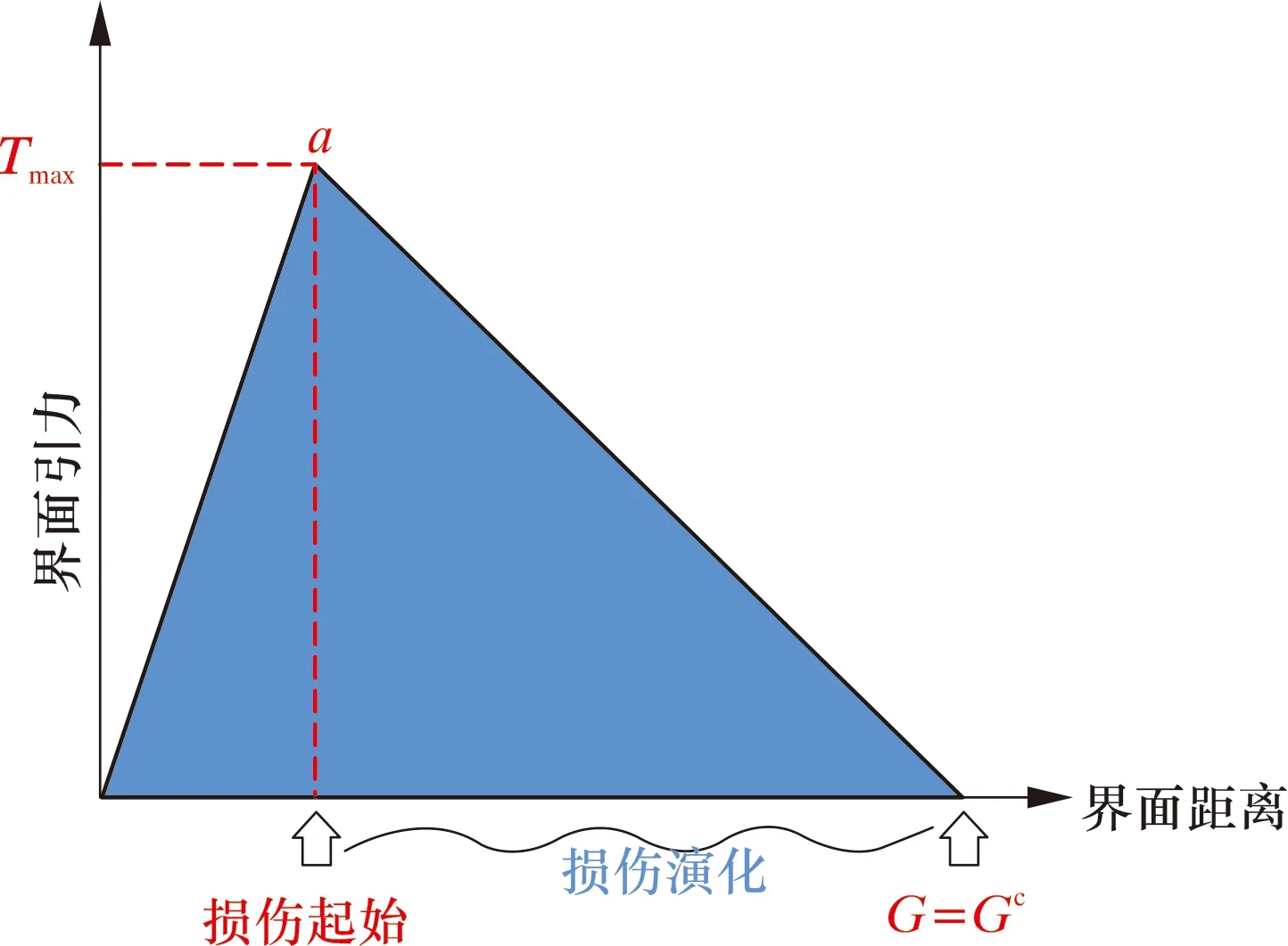
图3 牵引分离定律损伤准则示意图Fig.3 Schematic diagram of damage criterion of traction separation law

以二次应力准则判断裂缝是否开裂[25]：

(6)

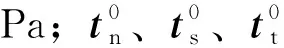
裂缝内部的法向应力和切向应力可以描述为：

(7)

(8)

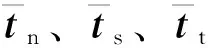
2.4 裂缝区的渗流和能量平衡方程

裂缝内部流体流动分为切向流和法向流，如图4所示。

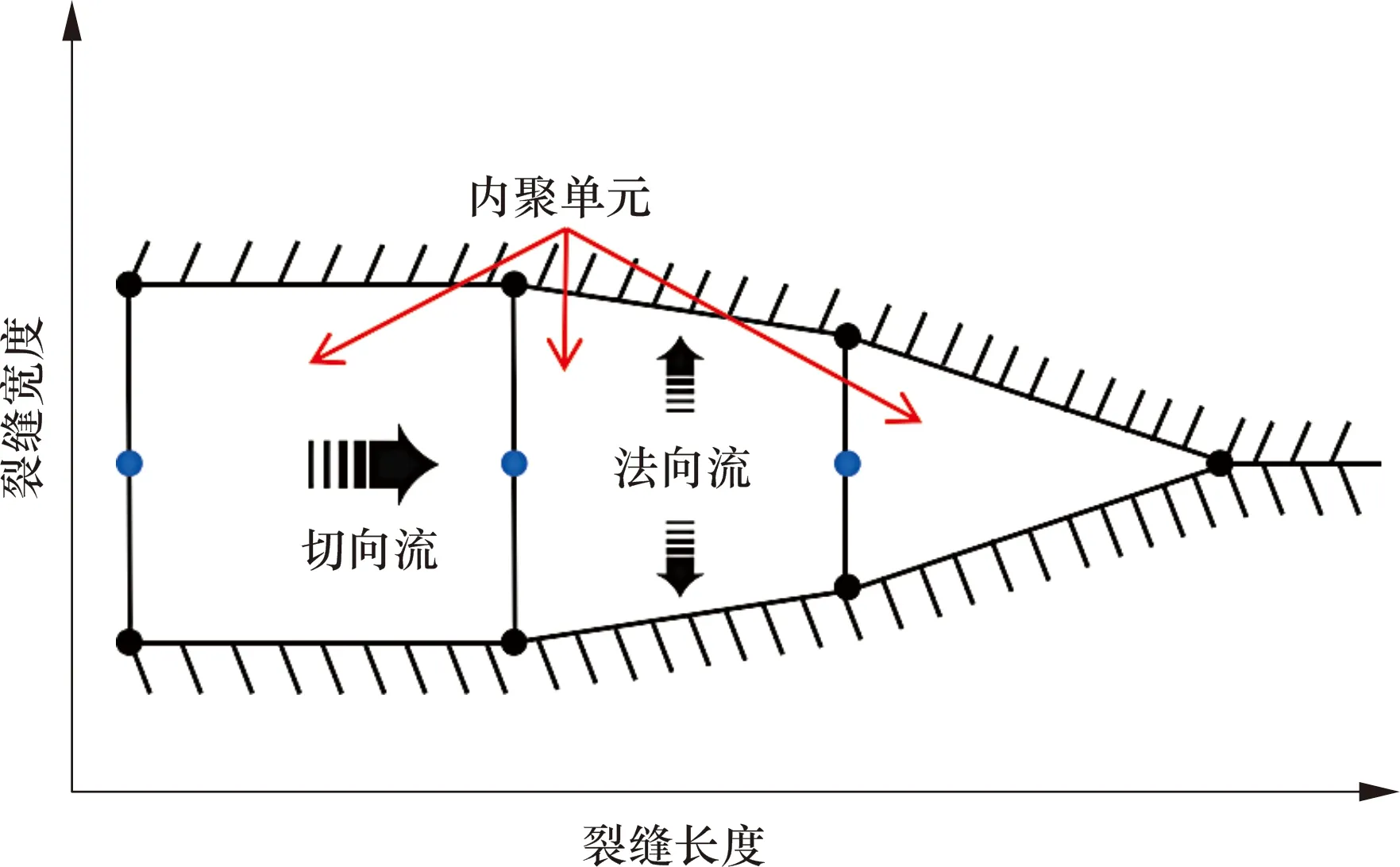
图4 Cohesive单元内部流动示Fig.4 Schematic diagram of internal flow of Cohesive unit

裂缝内法向流，即裂缝面和地层之间流体渗流方程为[26]：

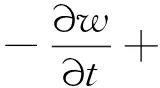
(9)

式中：q为切向流流体通量，m2/s；w为裂缝宽度，m；qt和qb分别是裂缝顶面和底面的法向滤失速度，m/s。

裂缝内切向流表示为[27]：

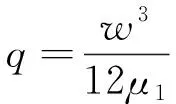
(10)

式中：μ1为流体黏度，mPa·s，pf为流体压力，Pa。

裂缝内考虑温度的能量平衡方程为[19]：

ρfCf[ct(pi-pt)+cb(pi-pb)]-

h(θ-θt)-h(θ-θb)=0

(11)

式中：ρf为流体密度，kg/m3；Cf为流体比热容，J/(kg·℃)；k为流体热传导系数，W/(m·℃)；h为对流换热系数，W/(m2·℃)；θ为裂缝内流体温度，℃；θt、θb分别为裂缝上、下表面的温度，℃；ct、cb为裂缝上、下表面滤失系数，m/(Pa·s)；pi、pt、pb分别为裂缝中间、底部和顶部的压力，Pa。

3 模型建立

3.1 几何模型

钻井液漏失模型如图5所示。使用管流(PIPE)单元建立U形管结构表征钻杆(绿色)和环空(黄色)。虽然U形管尺寸固定，但可通过调整摩擦因数等参数来等效不同井身结构。理论上，裂缝会沿最大水平地应力方向起裂和扩展，故预设一条与此方向平行的裂缝。该模型基于二维平面应变假设，只获取裂缝的长度和宽度。为减小计算量、提高收敛性和计算精度，建立地层模型，并将井筒附近的网格进行加密。为图示清楚，对图5中的井眼进行了放大(实际半径为10 cm)。模拟的实际工况为：深3 100 m、宽300 m、厚60 m的高温地层中的钻井液漏失。

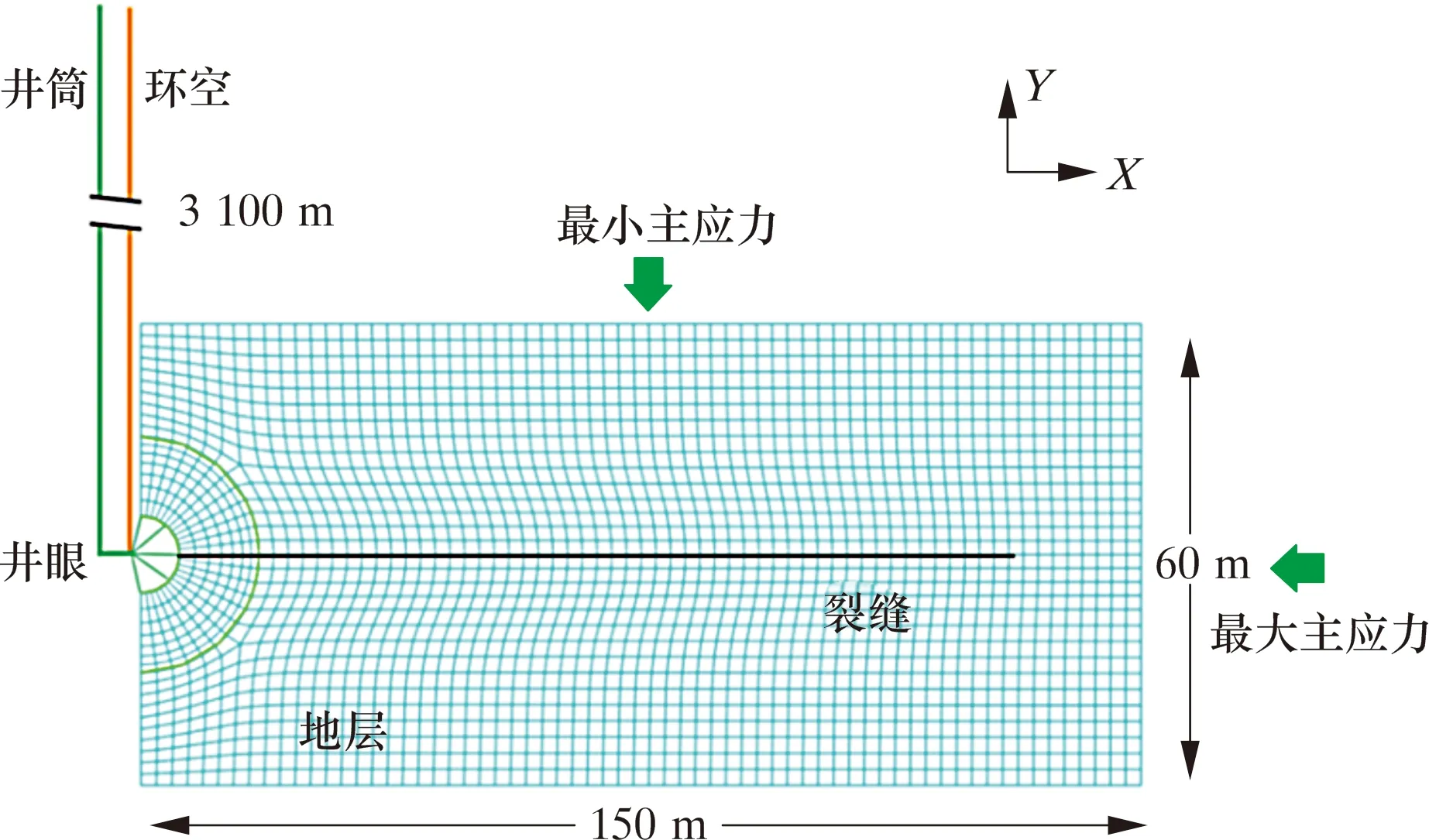
图5 钻井液漏失模型示意图Fig.5 Schematic diagram of drilling fluid loss model

3.2 初始和边界条件

以南海某高温高压区块为例，设置初始最大(X方向)、最小(Y方向)水平主应力分别为58.2、55.5 MPa；初始孔隙压力为44.8 MPa；初始孔隙度为15.7%；初始渗透率为5.3 mD。左侧施加对称边界条件，其他施加位移边界、孔隙压力边界和温度边界条件。井筒部分施加重力场、钻杆顶部的流量边界以及环空顶部的0压力边界条件，其他参数详见表1。

表1 模型的基础参数Table 1 Basic parameters of model

井筒与地层通过“Tie”和“PORMECH”关键词进行连接，实现钻井液在井筒和地层中的连续流动。“Tie”将井底节点与地层节点连接起来，保证井底与地层之间的压力、温度传递。“PORMECH”将井底压力施加到井壁上，模拟实际钻井时液柱对井壁的支撑力。通过这2个特殊约束，实现了井壁-裂缝-地层的热-流-固全耦合。

3.3 模拟步骤

地应力平衡步骤：计算井筒内静液柱压力，平衡地层中应力场、温度场、孔隙压力场，获取初始场平衡。

钻井液循环步骤：钻杆顶部注入钻井液，实现循环。若发生漏失，可获取漏失量、漏失速度、裂缝尺寸等相应数据。

基于上述模型，分别开展了等温和低温循环的数值模拟研究，探讨温度对钻井液漏失的影响。

4 结果与分析

通过设置不同排量的等温(钻井液温度100 ℃)和低温(钻井液温度30 ℃)对比模型来探究温度对钻井液漏失的影响。

4.1 钻井液温度对井周应力的影响

以0.094 m3/s排量，钻井液温度30和100 ℃为例，分析钻井液温度对井周应力的影响，结果如图6所示。如图6中蓝线所示，初始地应力平衡后，2个案例井周应力分布相同，均为压缩周向应力(正值代表拉伸，负值代表压缩)。最大值29.8 MPa，为Y方向；最小值13.4 MPa，为X方向。此状态下，Y方向更易发生井壁坍塌事故，X方向更易发生漏失事故。这与前人的研究规律相同[28-30]。

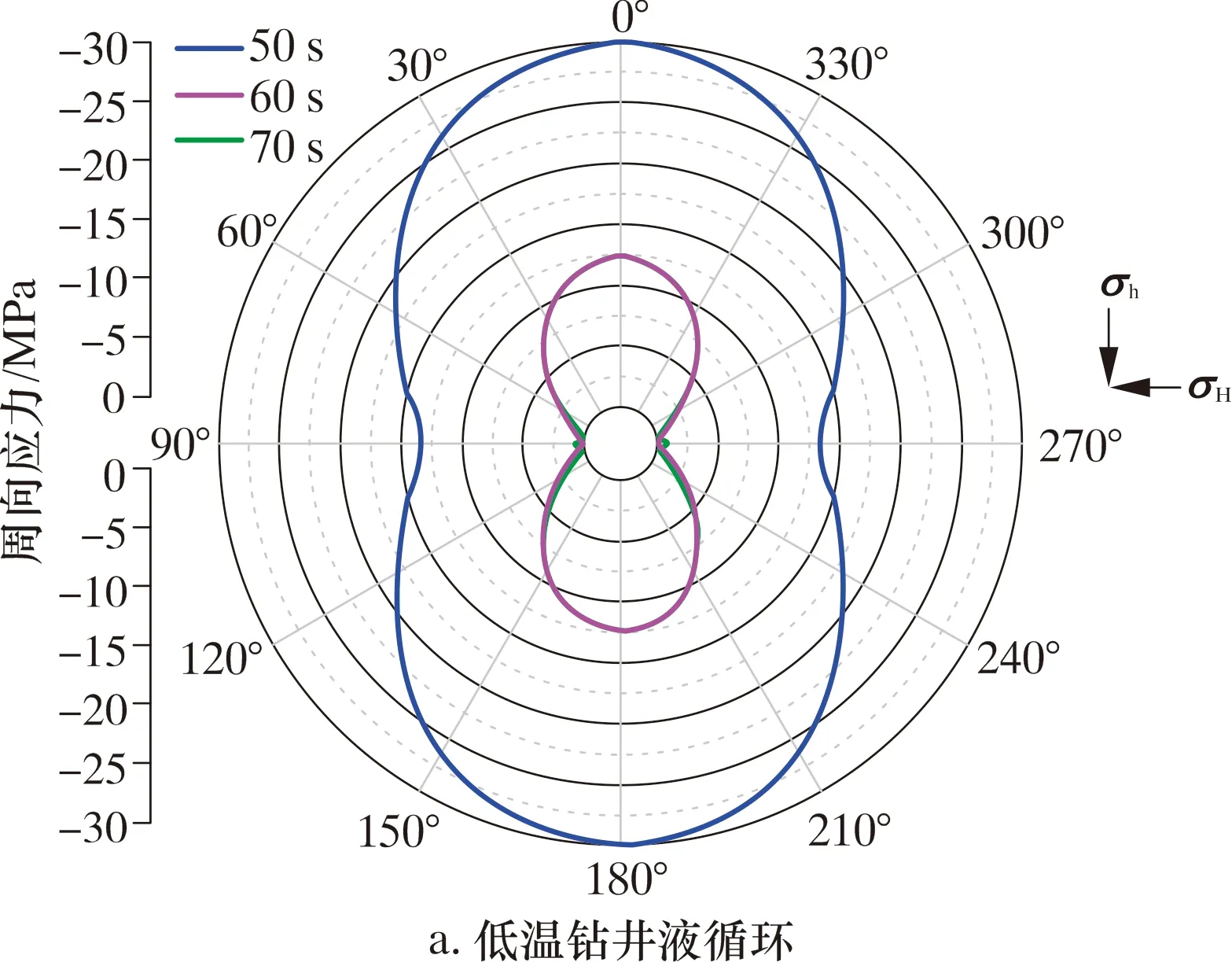
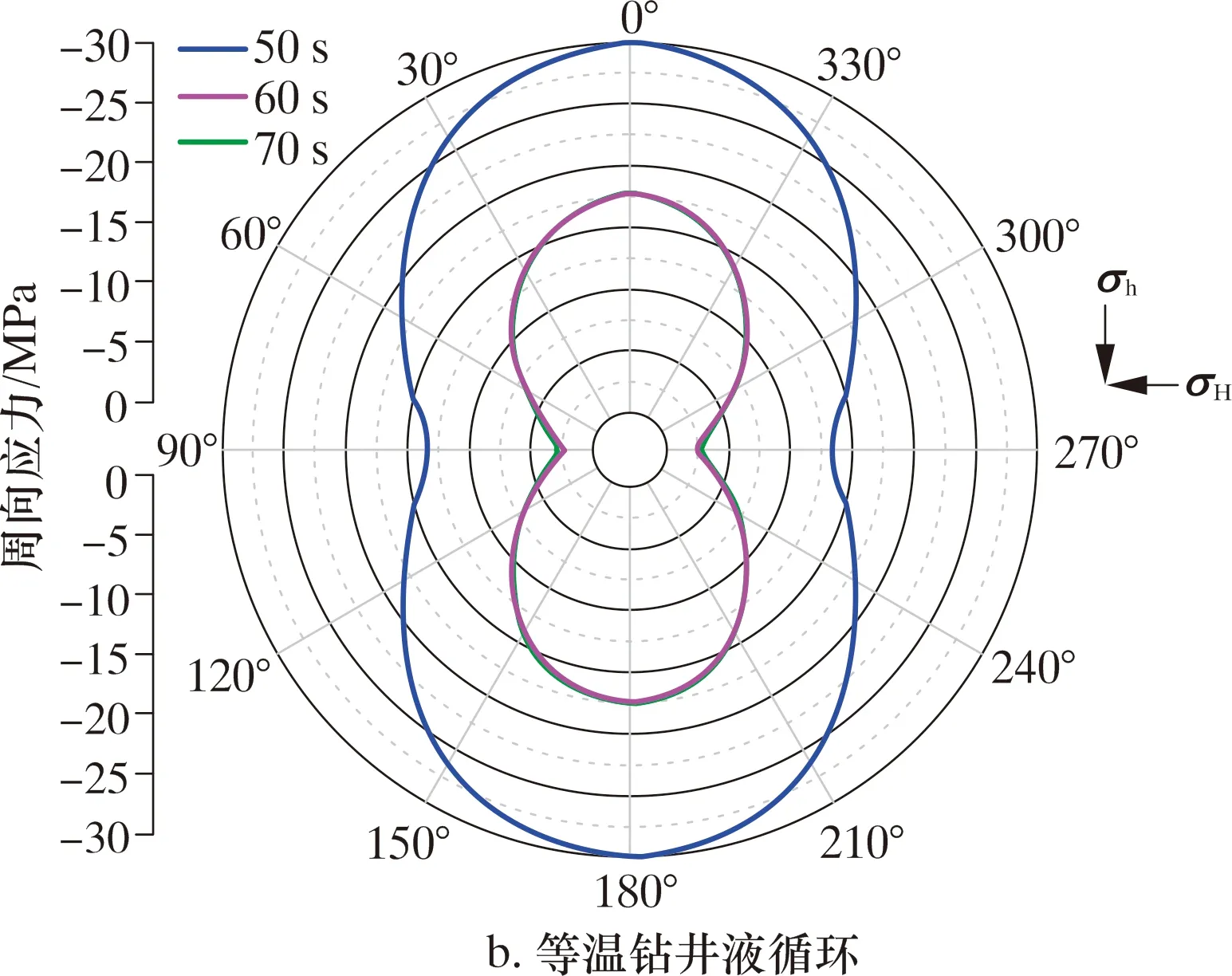
图6 井周应力分布Fig.6 Stress distribution around wellbore

当钻井液开始循环，井周应力显著减小。在60 s时，30 ℃钻井液循环的井周应力最大值、最小值分别为12.40和0.02 MPa，见图6a；100 ℃钻井液循环的井周应力最大值、最小值分别为17.8和2.8 MPa，见图6b。在该工况下，由于温度效应导致的井周应力最大值、最小值分别降低了30.3%和99.0%。70 s时井周应力继续缩小，但均与60 s时相差无几。据此可知，当钻井液温度低于地层温度时，会产生“冷却”效应，导致地层遇冷收缩，进一步降低井周应力，这将降低井壁坍塌风险，增大钻井液漏失风险。

4.2 钻井液温度对漏失裂缝起裂和扩展的影响

以0.094～0.100 m3/s(间隔0.002 m3/s)排量下的等温和低温模型模拟结果分析温度对漏失裂缝的影响。图7展示了相同排量下2种模型的裂缝长度随时间的变化规律。

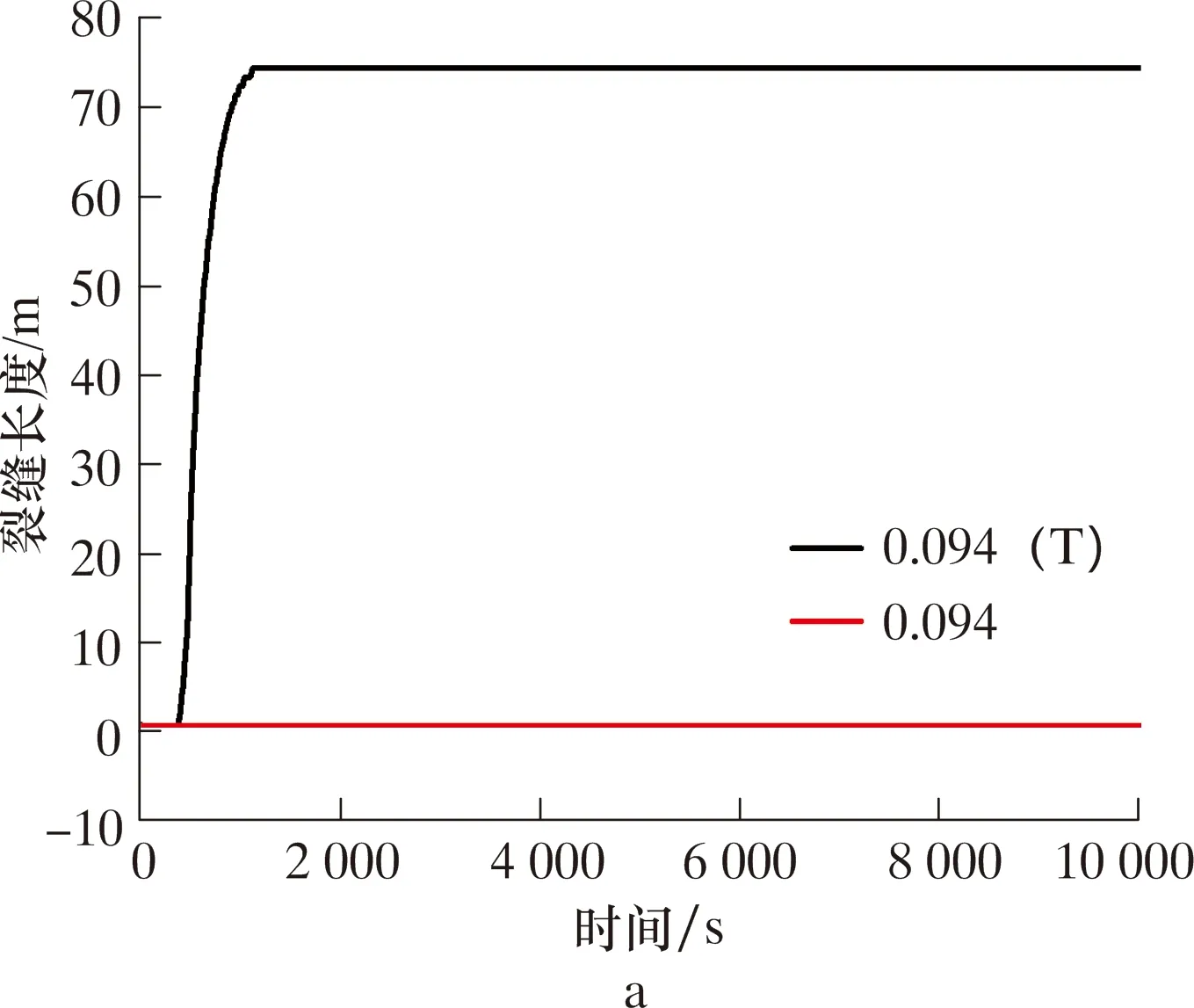
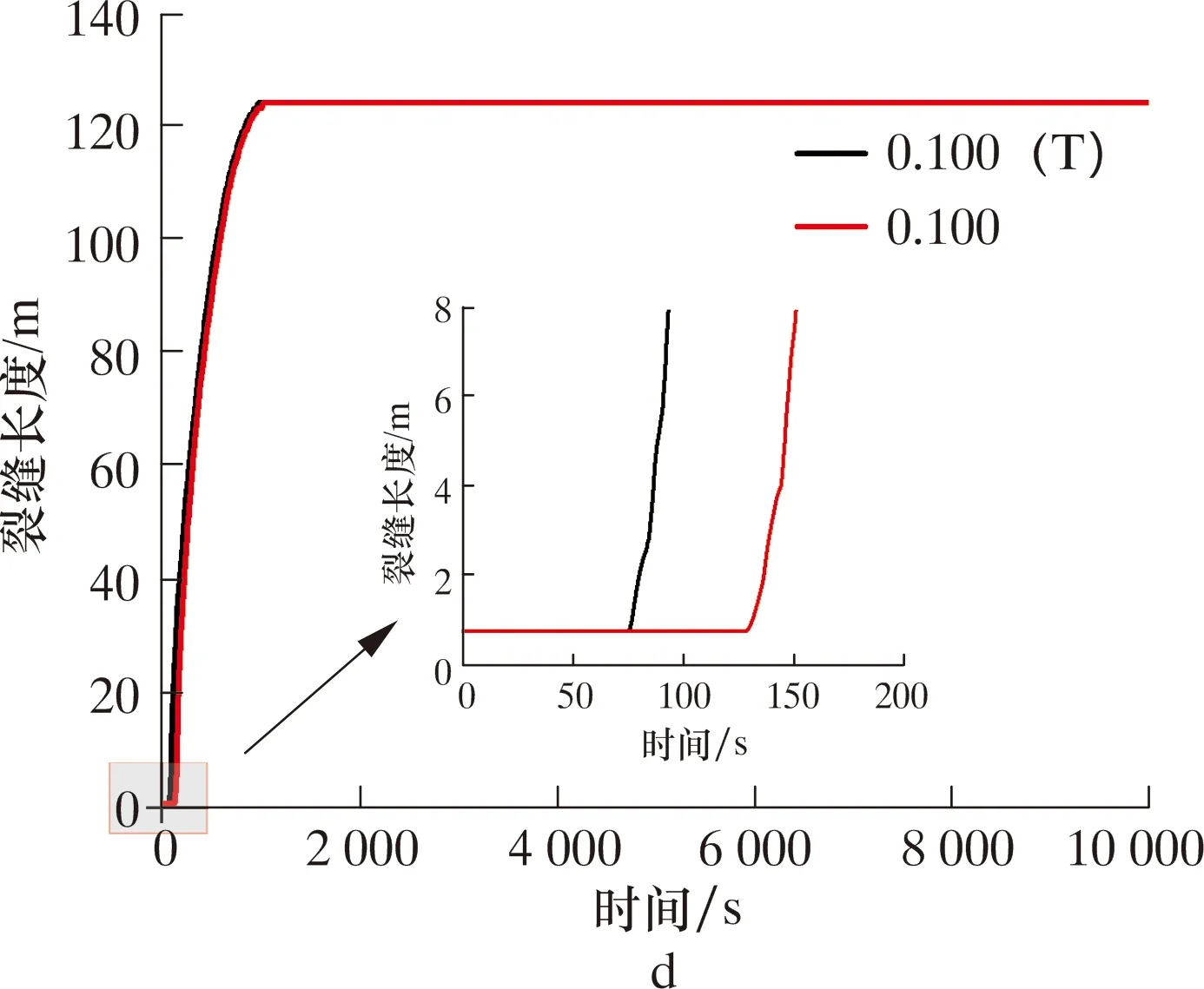
图7 裂缝长度随时间变化(带T的图例指低温注入模型)Fig.7 Change in fracture length over time (legend with T refers to low temperature injection model)

在0.094 m3/s排量下(见图7a)，等温模型未出现裂缝，未发生钻井液漏失，而低温模型在370 s开始出现裂缝并快速扩展，在1 104 s达到最大裂缝长度74.3 m。排量为0.096 m3/s时(见图7b)，2种模型均发生了钻井液漏失，但发生漏失的时间不同。低温模型在139 s发生漏失，在924 s达到最大裂缝长度88.4 m；等温模型则在679 s才出现漏失，并在1 320 s达到最大裂缝长度90.4 m。同样的，当排量增加至0.096和0.100 m3/s时，裂缝长度随时间的变化规律与0.096 m3/s时相同，且裂缝长度差异更小，见图7c、图7d。由此可见，当钻井液温度明显低于地层温度时，可降低漏失排量阈值，更小的循环排量即可诱发钻井液漏失。此外，相同排量下，低温钻井液循环发生的漏失更早。

提取最终的裂缝坐标并绘制裂缝剖面，如图8所示。

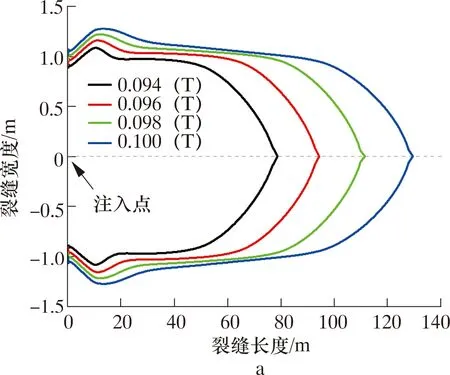
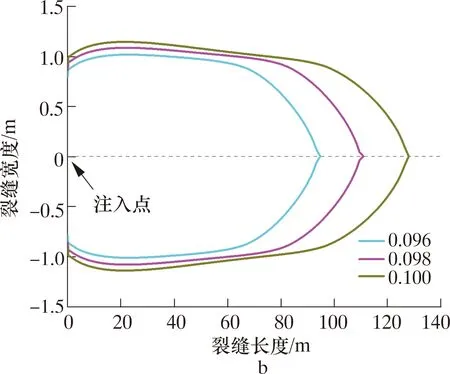
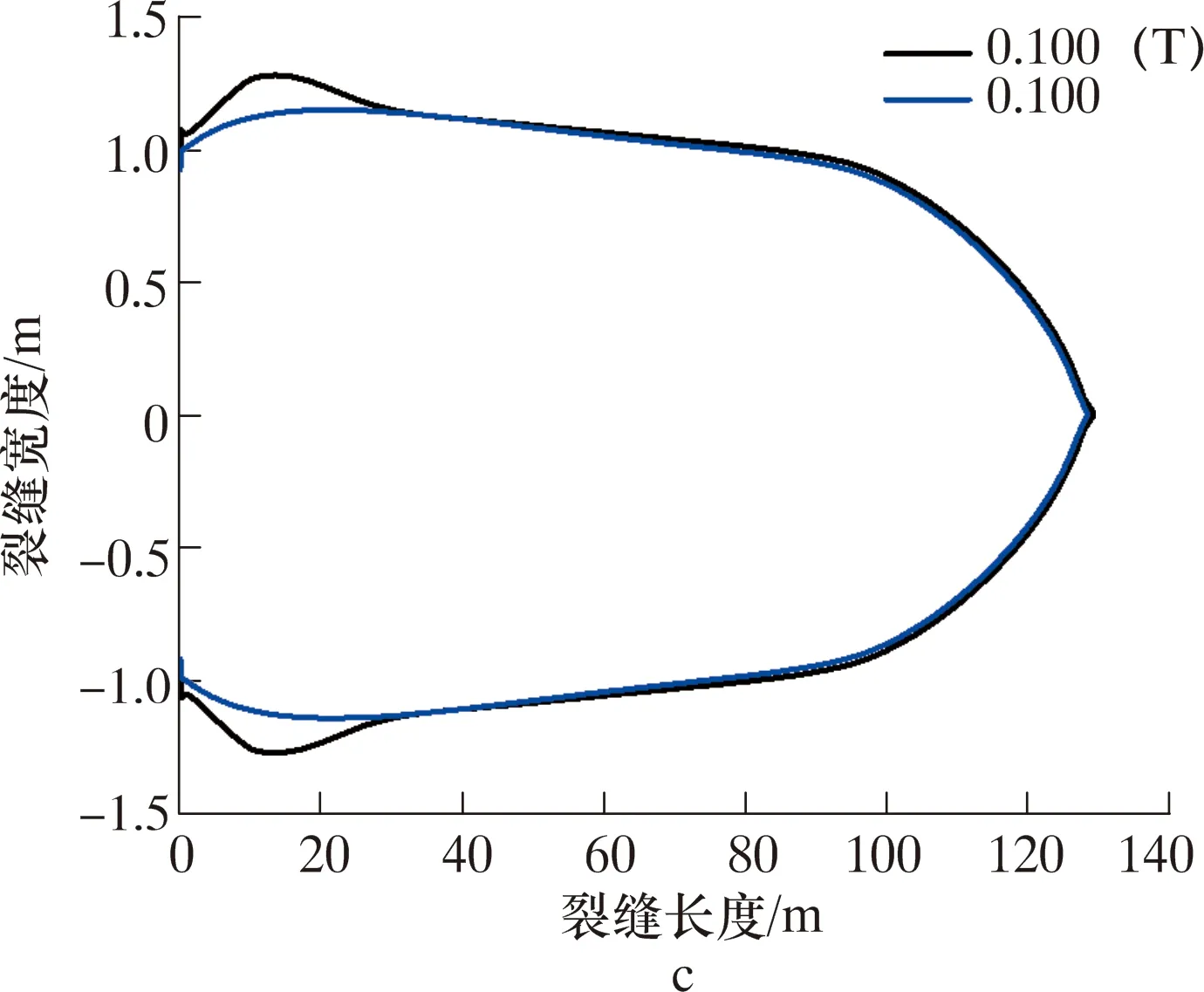
图8 不同排量下的裂缝剖面Fig.8 Fracture section at different displacements

从整体裂缝趋势来看，无论是低温循环(见图8a)还是等温循环(见图8b)，裂缝宽度整体表现为从井壁到远场呈现先增大后减小的趋势。原因在于，井壁附近有应力集中，裂缝最大宽度出现在靠近井壁的区域，而非井壁面上。但低温循环后在近井区域裂缝宽度明显增大，这是低温扩散到近井区域产生“冷却”效应，引起地层收缩。

以最大排量0.100 m3/s为例，对比循环后裂缝剖面，如图8c所示。低温循环和等温循环后裂缝长度相同，为124.4 m；距井壁30 m以远区域的裂缝宽度几乎相同。但在近井区域(<30 m)低温循环后的裂缝宽度明显更宽，最大宽度为2.54 mm，相较于等温循环最大缝宽(2.28 mm)增大11.4%。据此可知，低温钻井液循环对近井区域裂缝宽度影响明显，对远场区域裂缝尺寸无影响。

4.3 钻井液温度对漏失速度和漏失压力的影响

图9为相同排量下低温循环和等温循环的漏失速度随时间变化图。由图9可见，整体规律为低温循环漏失出现的更早，且峰值漏失速度略小于等温循环模型。以0.098 m3/s排量为例(见图9a)，低温循环的漏失发生时间为93 s，峰值漏失速度为0.001 4 m3/s，而等温循环的对应值为576 s和0.001 55 m3/s。

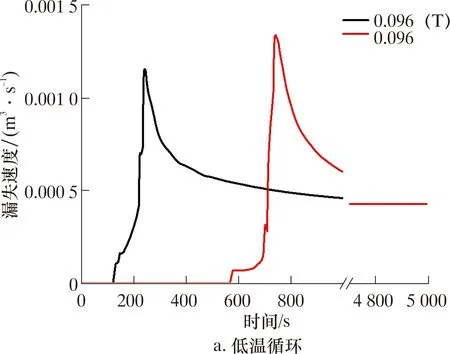
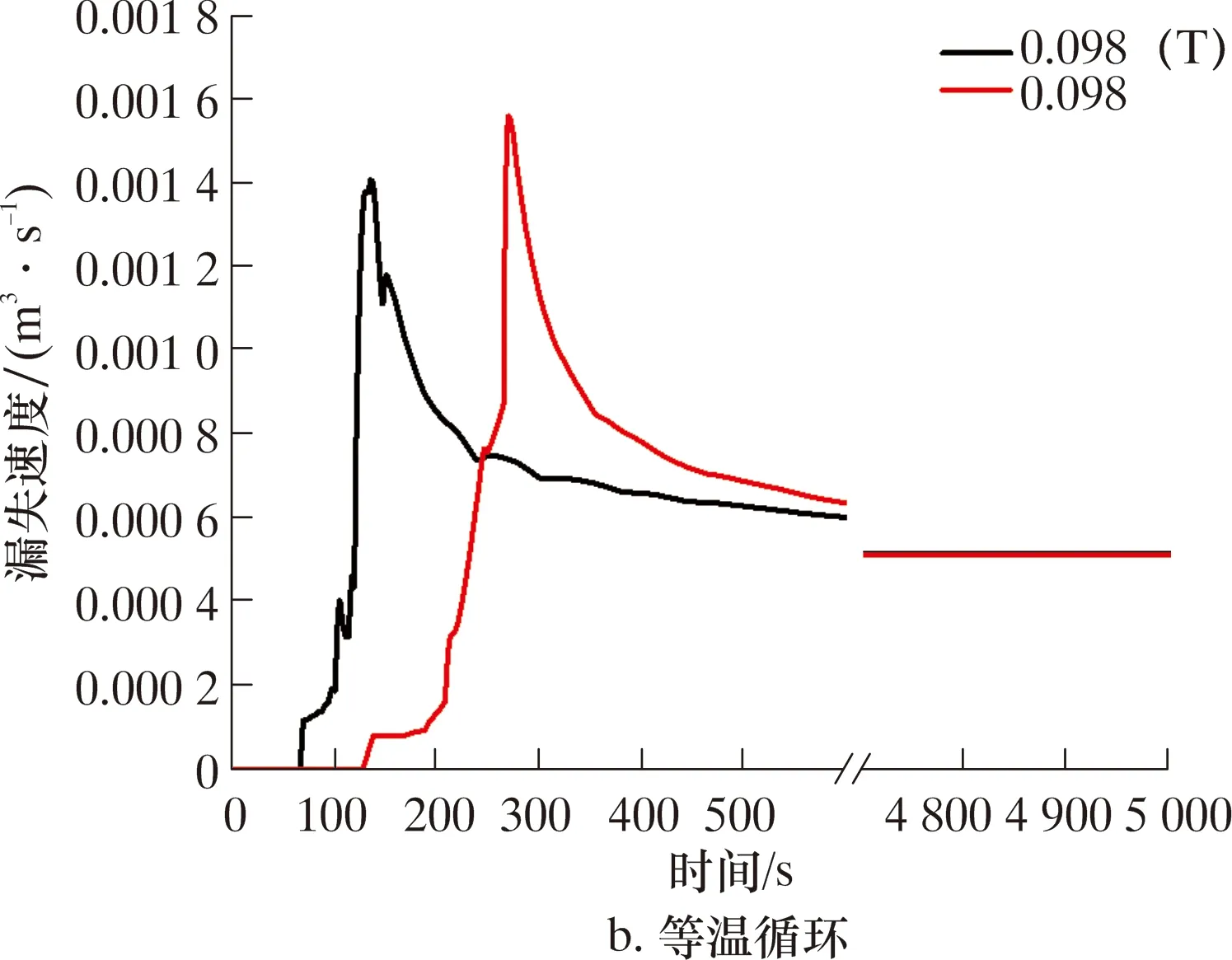
图9 漏失速度随时间变化Fig.9 Change in leak-off velocity over time

出现上述现象的原因在于模型中裂缝向地层内的漏失系数极低。因此，在发生漏失初期，漏失速度由裂缝的体积变化主导，当裂缝长度稳定后，漏失速度等于裂缝表面的滤失速度，而裂缝宽度的轻微增加，并不会显著增大漏失速度。结合裂缝长度随时间变化情况(见图7c)可知，无论是低温循环还是等温循环，漏失裂缝最终长度相同。而起裂和扩展总时间分别为565和386 s。据此可知，低温循环裂缝出现的早，但扩展较慢，而等温循环裂缝出现的晚，同时扩展速度快。故等温循环的峰值漏失速度要高于低温循环，最终稳定在相同的漏失速度。

漏失压力随时间变化如图10所示。对比漏失压力发现：在相同的排量下，低温循环的漏失压力略低于等温循环。在排量为0.094和0.096 m3/s时，裂缝延伸压力存在一定差异，但随着排量的增大，裂缝延伸压力相同。可见，排量大小是裂缝起裂和延伸的主导作用，温度只对漏失排量阈值影响较为明显。

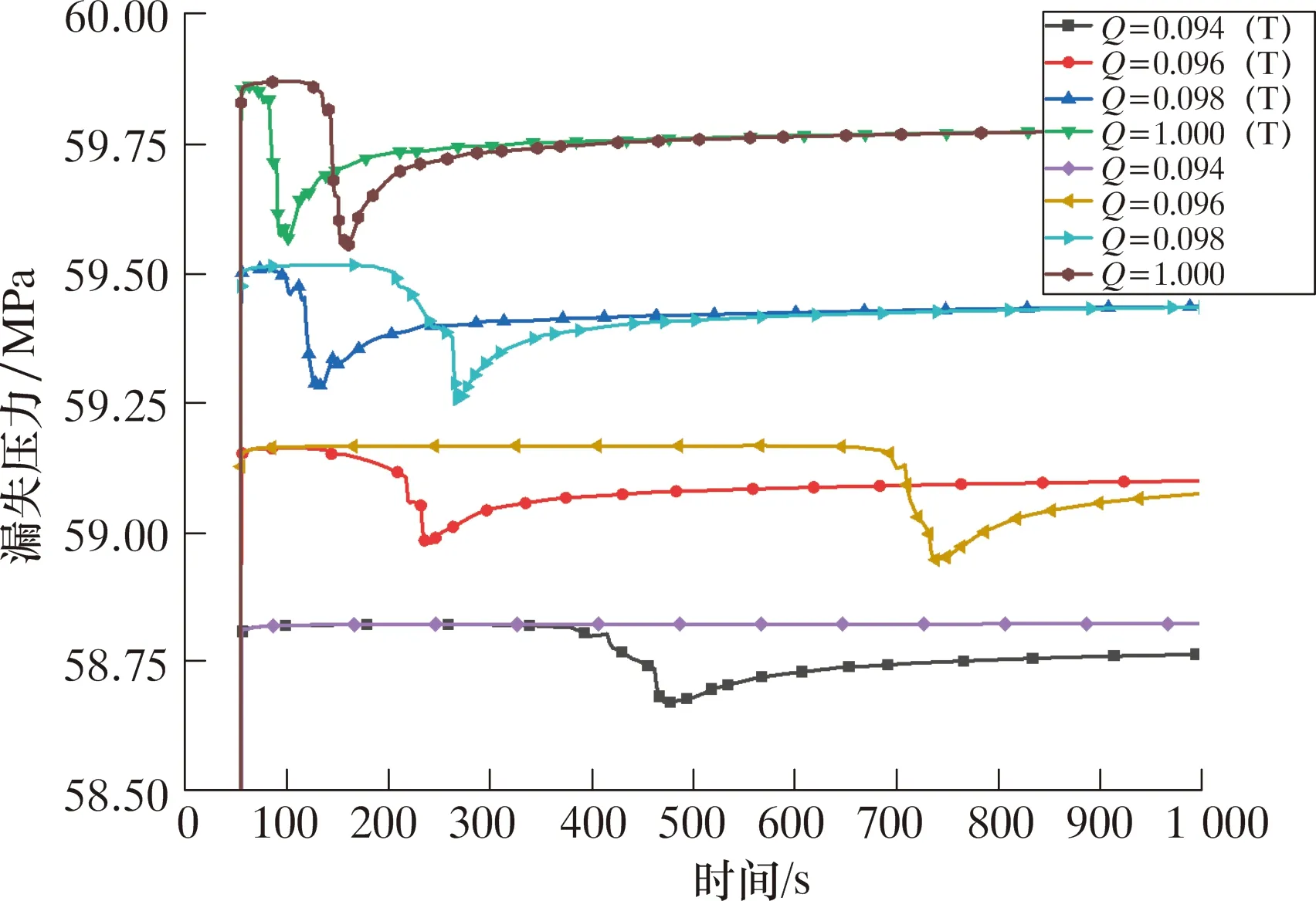
图10 漏失压力随时间变化Fig.10 Change in leakage pressure over time

4.4 钻井液温度对地层温度场的影响

钻井液漏失后最先进入裂缝，因此，相较于地层而言，裂缝中的温度场影响最为显著。以排量0.100 m3/s、钻井液温度30 ℃为例，分析低温钻井液对地层温度场的影响。图11展示了循环不同时间后，沿裂缝长度方向的温度分布。

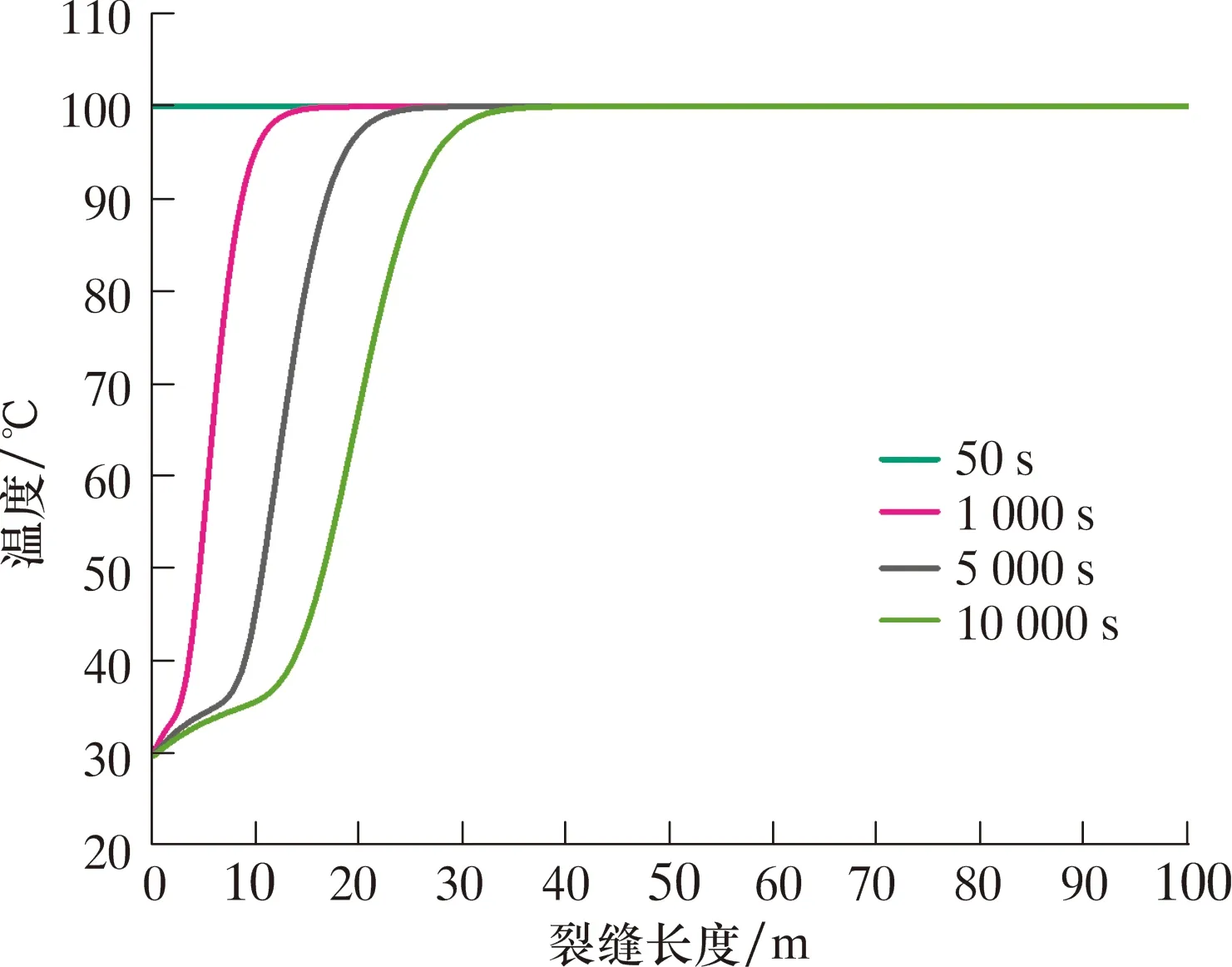
图11 不同时间裂缝内部温度分布(Q=0.096m3/s)Fig.11 Temperature distribution inside fracture at different times (Q=0.096 m3/s)

由图11可知：50 s时地应力平衡，裂缝内温度与地层温度相同；循环开始后，钻井液漏失进入裂缝，近井区域温度降低；在1 000 s时，裂缝内温度场波及长度约10 m，而此时漏失裂缝长度已经超过100 m(见图7d)；随着循环时间的延长，钻井液持续向地层内漏失，裂缝内的温度场波及范围增大，5 000 s时，波及范围约22 m；最终，波及范围约35 m。可见，温度场的波及速度要远比漏失钻井液波及速度“慢”。

钻井液漏失只对近井区域的温度场产生影响，并未波及远场。这进一步证明了相较于等温循环，低温循环的近井区域裂缝宽度变化明显，井周应力变化大，漏失压力减小，而裂缝长度、延伸压力相同的现象。

综合裂缝长度、宽度和裂缝内温度的模拟结果，虽然低温钻井液循环会降低井周应力，更早地诱发裂缝，但短时间内主导裂缝起裂和扩展的是排量。另一方面，由于井筒内循环的钻井液体积有限，所携带的热能相对较小，仅能影响近井区域和近井裂缝内的温度分布，因此“冷却”效应对于裂缝长度的影响极小。