十字万向轴多体动力学仿真与啮合面磨损机理*

2023-07-22张锐尧叶道辉朱忠喜关勤勤明瑞卿

石油机械 2023年7期

张锐尧叶道辉朱忠喜全兵肖平关勤勤明瑞卿

(1.中石化石油机械股份有限公司 2.长江大学石油工程学院 3.中石油勘探开发研究院)

0 引言

近年来，随着我国油气资源勘探开发力度日益增大，仅仅对浅部地层油气资源的开采已经不能满足现有需求。未来我国油气勘探开发的重点目标是各类“难动用”的油气资源，尤其是大量深井、超深井、大位移井等复杂结构井，这使得钻井提速难题异常凸显，因此亟需开展相关提速工具的研究[1-4]。

螺杆钻具作为常用的钻井提速工具，可以将钻井液的水力能作为动力源转化为钻头所需要的机械能，由钻井液驱动马达转子旋转，进而把扭矩和转速持续不断地传递给钻头，再带动钻头旋转钻进，从而实现安全、高效钻井，缩短钻井时间，降低钻井综合成本。特别是螺杆钻具与PDC钻头配合使用时具有恒定的机械转速，能保持钻头高效切削，可以降低扭转振动、减小钻头黏滑卡阻，减缓PDC钻头复合片的崩片、磨损，从而提高破岩效率。螺杆钻具的关键传动结构-万向轴的使用寿命对工具整体的使用寿命具有决定性影响。然而，现有挠性万向轴由于长度大，不利于定向钻井作业，不适用水平井和大位移井[5]；瓣式万向轴在传递运动过程中，瓣齿之间会产生滑动摩擦，运动副的磨损也比较严重[6-7]；球形万向轴为了增加耐磨性，则需要对运动副外表面做特殊强化处理，并且对密封性能的要求较高[8-10]。虽然现有非密封式十字万向轴既避免了密封失效带来的不利影响，同时又具有球形万向轴灵活运动的优势特点。但是，目前对于该结构所产生的运动磨损机理研究较少。为此，笔者结合十字万向轴的运动特点与实际工况条件，开展了多体动力学仿真分析，以探究十字万向轴共轭运动副啮合面的运动规律以及磨损机理。

1 多体动力学仿真分析

1.1 结构及工作原理

十字万向轴结构如图1所示。十字万向轴主要包括上接头、中间轴、下接头、球座与锁紧轴。万向轴的上接头与马达转子通过螺纹连接，下接头与传动轴总成同心连接。转子偏心旋转运动的转速和输入扭矩经过上接头与中间轴以及中间轴与下接头之间形成的共轭运动副传递后，偏心旋转运动转变为下接头的定轴旋转运动。共轭运动副实现运动的传递，一方面主要是通过锁紧轴的球头与球座之间同球心配合来实现 “十字”运动，另一方面则通过上接头与中间轴以及中间轴与下接头之间形成的啮合面进行扭矩和转速的传递。

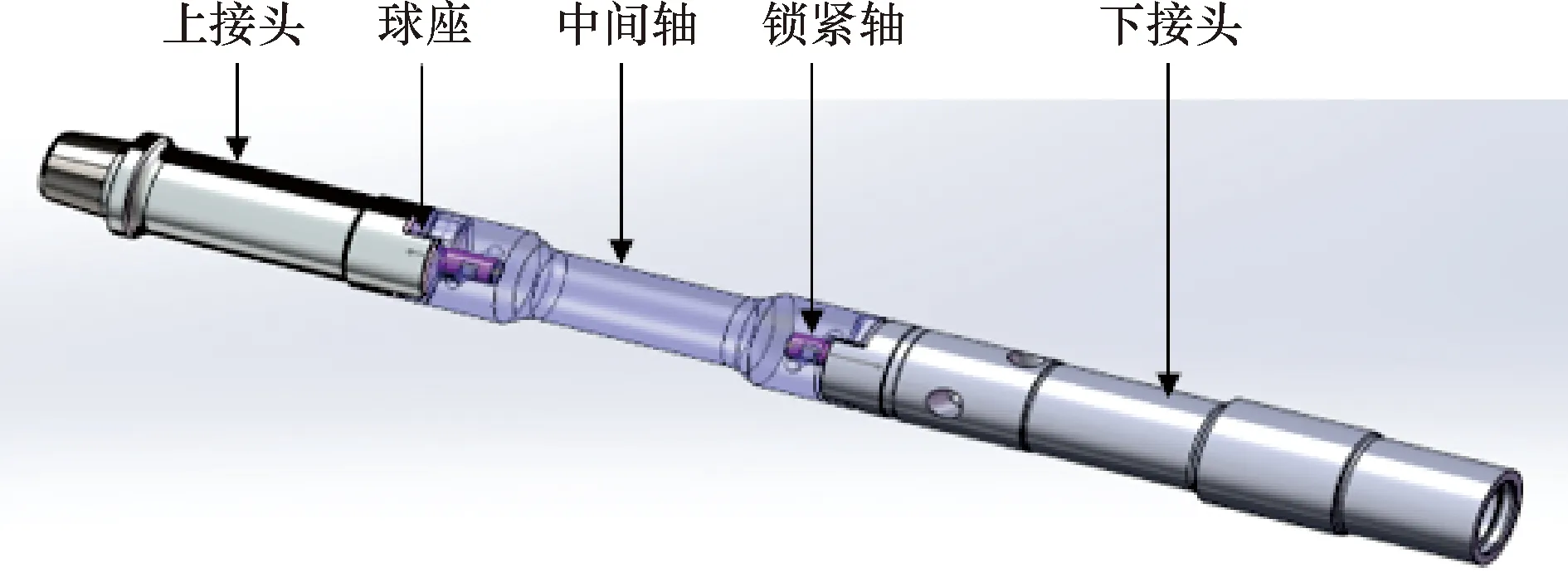
图1 十字万向轴结构Fig.1 General structure of the cross cardan shaft

1.2 数学模型

十字万向轴在运动过程中，上接头承受载荷后产生一定的转速，并利用共轭接触区将扭矩传递给中间轴和下接头，从而实现力和运动的传递。假设万向轴各部件为刚体，因此其运动过程可以用多刚体运动学进行描述。

多体动力学的控制方程建模包括相对坐标的拉格朗日法和绝对坐标的笛卡尔法[11-13]。本文使用笛卡尔法建立动力学控制方程，该建模方法虽然方程数量大，但是其系数矩阵稀疏，建模更简单且其雅克比矩阵具有线性特征，因此计算效率更高[14-15]。动力学控制方程为：

(1)

式中：m为机械系统惯性矩阵；n为外力向量；L为位置坐标阵；Θq为约束方程的雅克比矩阵；λ为拉格朗日乘子；q为系统位置向量；t为时间。

对笛卡尔法建模所得动力学控制方程，可以根据拉格朗日乘子与位置坐标矩阵的处理差异[16]，将式(1)转化为：

(2)

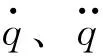
基于式(2)对t求导，可以得到：

(3)

给定初始条件：

(4)

对控制方程进行求解。

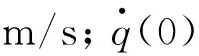
多体动力学中的碰撞可以视为变结构的动力学问题，与系统发生碰撞前进行对比，可知十字万向节的碰撞接触模型应为接触变形模型[17-18]。该模型以精确的刚体碰撞过程为基础，通过计入接触面的弹性和阻尼，实现对运动过程的描述，并进一步建立力和接触变形之间的本构关系。由于非线性等效弹簧阻尼模型可以更真实地反应运动规律，更准确地计算接触碰撞过程中的实际能量损耗，所以选择该模型进行计算。其中，该模型的广义表达式为：

(5)

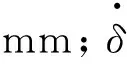
在运动过程中，由于需要考虑动摩擦因数和静摩擦因数，所以对式(5)进行整理，可以得到由法向碰撞和摩擦力构成的总的接触力为：

(6)

式中：FN为法向碰撞力，N；Ff为摩擦力，N；C(δ)为考虑动静摩擦的综合摩擦因数。

1.3 物理模型

在钻井过程中，十字万向轴上接头与马达转子同轴线安装且做偏心旋转运动，并承受转子的轴向载荷和扭矩。为了更好地模拟十字万向轴在井下的实际工况条件，应设定公转盘和底座相关参数。其中公转盘的内腔与外轮廓之间的偏心距设定为9 mm，上接头与内腔同轴心安装，使得上接头可以保持定速偏心旋转运动，下接头与底座同轴心安装且为定轴旋转，底座保持固定。十字万向轴多体动力学仿真物理模型如图2所示。

图2 十字万向轴多体动力学仿真物理模型Fig.2 Multi-body dynamics simulation physical model of the cross cardan shaft

设置材料为42CrMo，弹性模量为210 GPa，泊松比为0.33，密度为7 880 kg/m3，抗拉强度1 080 MPa，屈服强度为930 MPa，公转盘的转速为100 r/min，上接头输入扭矩为20 kN·m，轴向力为10 kN。中间轴与上、下接头之间的接触关系采用精确接触，精度为0.001，3D接触分辨率设置为最高。设置每秒帧数为100，雅克比验算调整为最高等级。

由于WSTIFF积分器为变量阶序、变量步长大小的刚性积分器，当存在不连续力、不连续运动或者具有3D接触时，该算法中所使用的系数可以随步长做动态调整，从而可以在保证计算速度的条件下，提升仿真计算的精度。对应的求解流程如图3所示。

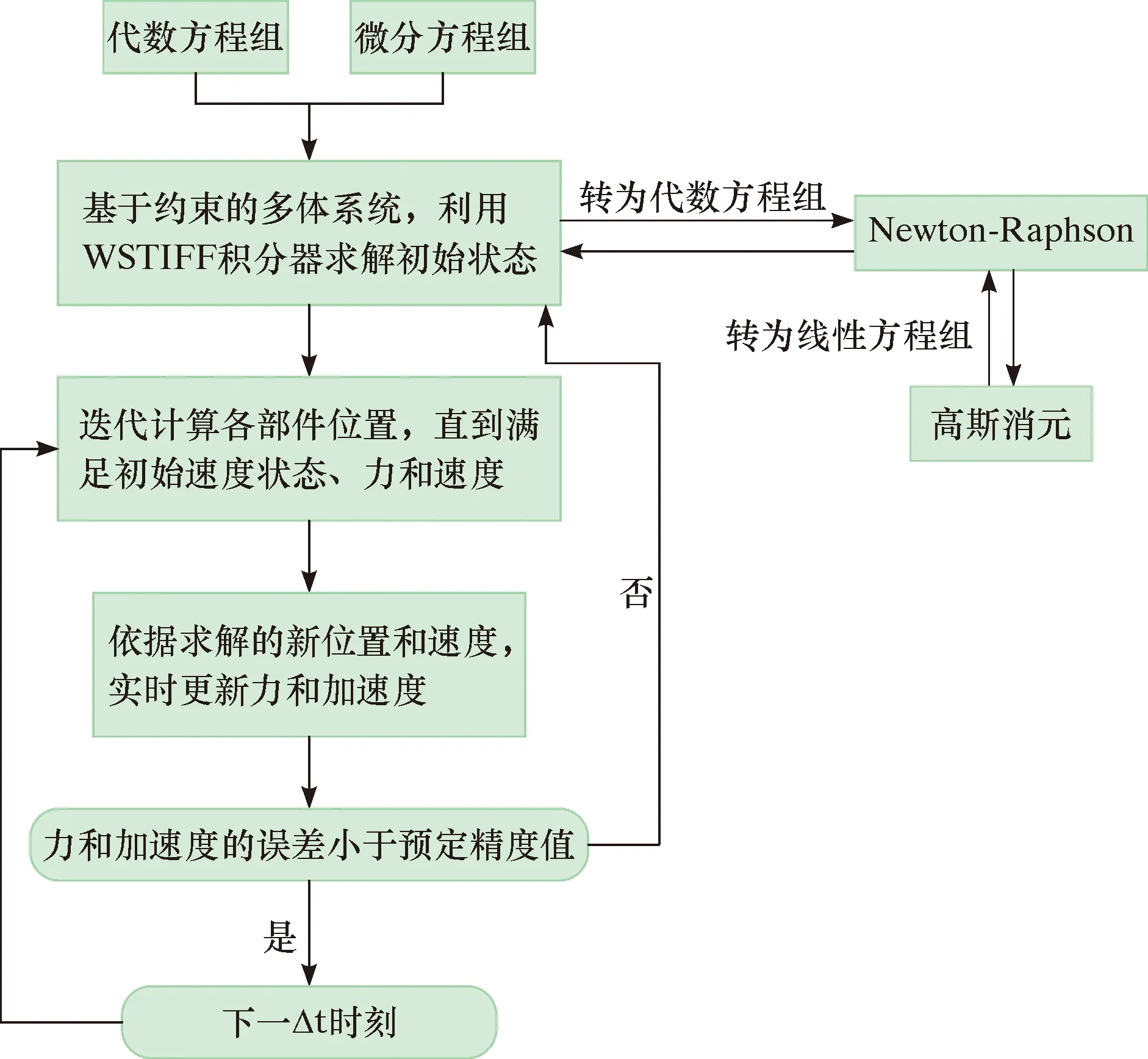
图3 十字万向轴多体动力学模型求解流程Fig.3 Solution process of the multi-body dynamics model of the cross cardan shaft

2 啮合面磨损机理分析

2.1 仿真结果

对动力学模型进行求解，得到结果如图4和图5所示。从图4a和图4b中可知，上接头与中间轴的运动接触主要包括2个阶段。在运动接触的第1阶段，接触力和摩擦力出现突然增大或减小的无规则分布状态，总体为增加的趋势；当进入运动接触的第2阶段，此时接触力与摩擦力先减小，然后增大，并且呈现周期性变化规律。

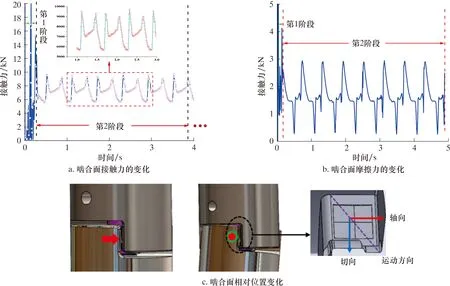
图4 十字万向轴的中间轴与上接头的啮合面接触力、摩擦力与相对位置分析Fig.4 Contact force，friction and relative position of the mating surfaces between the intermediate shaft and the upper joint of the cross cardan shaft

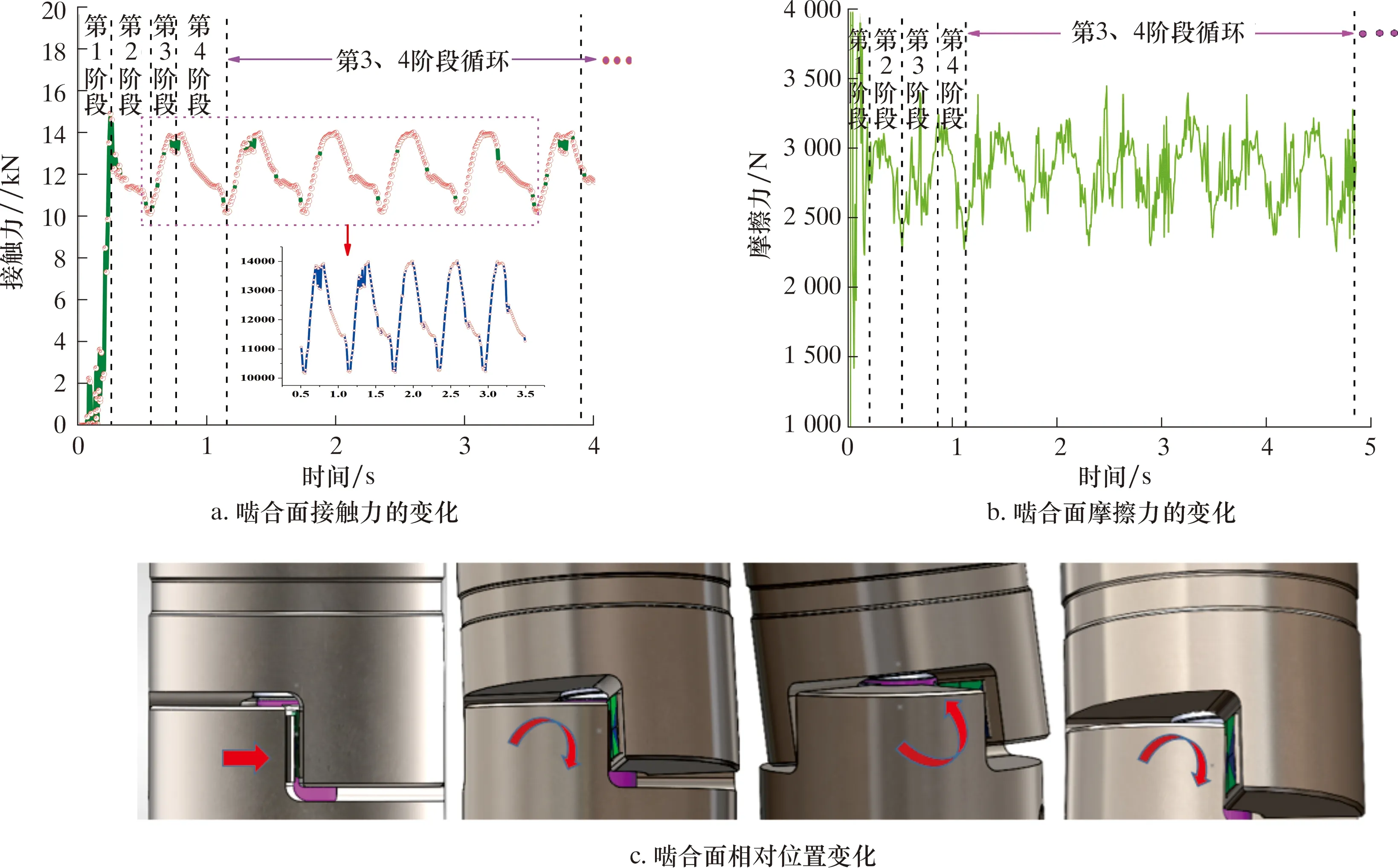
图5 十字万向轴的中间轴与下接头的啮合面接触力、摩擦力与位置分析Fig.5 Contact force，friction and position of the mating surfaces between the intermediate shaft and the lower joint of the cross cardan shaft

将求解所得的同一时间条件下的接触力和摩擦力(见图4a和图4b)与对应该时刻的运动位置(见图4c)进行同步对比分析可知：图4a中的第1阶段与图4c左图对应，此时上接头在扭矩作用下且以一定的转速对中间轴的啮合面产生法向碰撞，此时运动啮合状态不稳定，会在2个啮合面之间产生碰撞、滑动等运动，随着接触面积逐渐增大，接触力也逐渐增加。第2阶段与图4c右图对应，此时上接头相对于中间轴沿着啮合面的切向(与旋转方向相同)方向摆动，所以2个啮合面之间出现一定的夹角，随着接触面积逐渐减小，两者之间的接触力和摩擦力逐渐减小；当上接头向该运动方向的反方向摆动时，则啮合接触面积逐渐增大，此时接触力和摩擦力又开始逐渐增加；随着运动继续传递，两者的啮合达到稳定状态。总之，接触力和摩擦力最终呈现周期性波动规律(见图4a和图4b)，2个啮合面之间呈现较小区域的滑动摩擦运动状态。

中间轴与下接头之间的运动接触过程包括4个阶段(见图5a)。在运动接触的第1阶段，接触力和摩擦力出现突然增大或减小的无规则分布状态，但是总体呈现逐渐增大的趋势；当进入运动的第2阶段时，接触力和摩擦力又由峰值呈现逐渐减小的趋势；当运动到第3、4阶段时，接触状态达到相对稳定，接触力和摩擦力总体呈现先增大又减小的周期性波动规律。

同理，将求解所得的同一时间条件下的接触力和摩擦力(见图5a和图5b)与对应时间的运动状态(见图5c)进行同步对比分析可知：图5a和图5b中的第1～4阶段接触力与摩擦力的变化与同时刻条件下的图5c中从左至右呈现的运动位置对应。在第1阶段，上接头在扭矩作用下且以一定的转速对中间轴的啮合面产生法向碰撞，随着接触面积逐渐增大，接触力和摩擦力也逐渐增加；第2阶段，中间轴沿着与下接头啮合面的切向方向摆动，此时2个啮合面之间呈现滑动摩擦的运动状态且接触面积逐渐减小，导致接触力与摩擦力逐渐减小。当运动到极限位置时，接触力和摩擦力都减小到极小值，所以该阶段为过渡阶段；第3阶段，当中间轴从极限位置向该运动方向的反方向摆动时，则啮合接触面积逐渐增大，此时接触力和摩擦力又开始逐渐增大；在第4阶段，接触力和摩擦力又随着接触面积减小而逐渐减小。随着运动继续传递，两者的啮合状态达到稳定状态，中间轴与下接头保持第3、4阶段所示的周期性滑动摩擦运动。

2.2 现场试验结果

为了进一步研究十字万向轴在井下实际工况条件下的磨损情况，将其与ø244 mm螺杆钻具在焦页165-1HF井中进行现场试验。工况参数：排量为65～70 L/s，泵压为15～18 MPa，转速为50～60 r/min。

图6为不同地层段钻压和扭矩变化情况：第一趟钻位于嘉陵江组-龙潭组，机械钻速为14.36 m/h，实际钻进深度为75 m，有效使用时间为82 h；第二趟钻位于龙潭组-茅口组，实际钻进深度为197 m，机械钻速为8.3 m/h，有效使用时间为31 h。

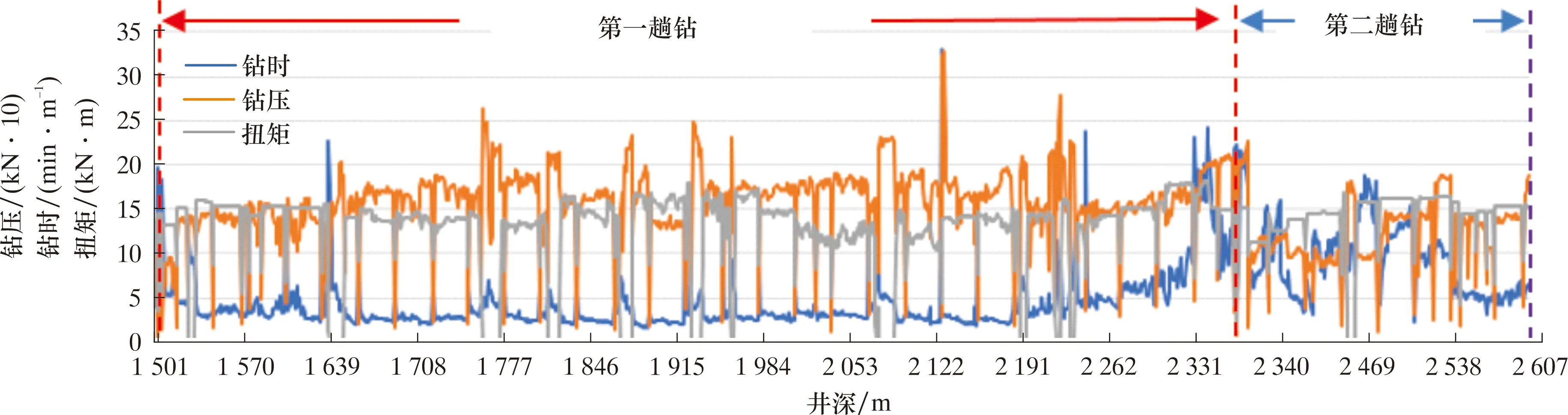
图6 焦页165-1 HF井每米钻时及钻压、扭矩曲线Fig.6 Curves of drilling time，WOB and torque for Well Jiaoye 165-1 HF

3 结果对比分析

中间轴与下接头仿真计算结果与现场测试结果对比如图7所示。图7a和图7b为为十字万向轴中间轴与下接头的现场测试结果，啮合面出现严重磨损的部位位于区域1和区域2，沿着区域1的切线方向，内侧磨损量大，外侧磨损量小；沿着区域2的轴向方向，外侧磨损量大，内侧磨损量小。图7c为中间轴与下接头的接触力仿真结果，当运动时刻位于图7a位置时，啮合面接触力达到波峰值，啮合面端面的接触区正好为区域1；当运动到图7b位置时，此时接触力为波谷值，啮合面侧面接触区为区域2。当十字万向轴在传递扭矩和转速时，区域1和区域2之间的啮合面出现周期性往复摩擦运动，接触力和摩擦力为周期性波动，所以接触区域产生周期性磨损，最终导致在啮合面端面内侧磨损多，外侧磨损少，在啮合面侧面形成内侧磨损少，外侧磨损多的形态特征。