MPSK信号类内调制样式识别研究
2023-07-17黄刚
黄 刚
(中国电子科技集团公司第二十研究所,陕西 西安 710068)
0 引 言
调制样式是不同通信体制信号的重要特征。在非合作通信中,信号的调制样式识别是十分关键的技术。截取电磁波信号,分析识别信号的调制方式,估计信号的相关参量,为接收解调设备解析信号内容提供了重要的理论依据。随着无线电技术飞速发展,不断涌现出各种新型调制技术。多进制相移键控调制(MPSK)具备传输频带利用率高、抗干扰能力强等特点,被大量应用于卫星通信、遥控测量、电台等多种无线通信系统。为了实现有限带宽内传输容量扩大,MPSK调制技术从二进制相移键控(BPSK)发展到正交相移键控(QPSK)、八进制相移键控(8PSK)等高阶相位数字调制。同时,为了使得调制波形具备更好的恒包络特性,减小射频功率器件的非线性造成的功率谱旁瓣增生效应,在QPSK基础上又发展了偏移四相相移键控(OQPSK)、π/4-QPSK,它们具备了更小的相位跳变,使得信号包络特性更好。因此,研究MPSK类内(BPSK、QPSK、OQPSK、π/4-QPSK、8PSK)信号调制样式的识别具有重要的现实价值。
文献[1]提出了根据不同调制信号的相位直方图统计识别BPSK、QPSK、OQPSK信号调制样式,但是该方法受噪声干扰较大,识别不稳定。文献[2]提出采用四阶和六阶累积量识别BPSK、QPSK、8PSK,但是OQPSK和QPSK、8PSK和π/4-QPSK的累积量相同,无法实现这几种信号类内识别。文献[3]提出基于差分星座进行多级聚类的方法识别π/4-QPSK和8PSK信号调制样式。文献[4]提出了一种基于信号的四阶、八阶累积量作为特征识别BPSK、QPSK、π/4-QPSK和8PSK调制信号,但是计算信号的八阶累积量运算较为复杂。本文提出了一种基于信号四阶累积量和差分星座最小环带方差联合特征识别BPSK、QPSK、OQPSK、π/4-QPSK和8PSK调制信号,该方法能够较好地识别MPSK类内几种信号,同时对于载波残余相位不敏感,计算复杂度较低。
1 信号模型
本文假设接收信号已载波恢复和定时同步,其表示为:
(1)
式中:a(k)表示码元序列,k=1,2,…,N,N表示码元长度,a(k)∈{ej2π(m-1)/M,m=1,2,…,M},M表示调制相位进制,本文中对于BPSK、QPSK和8PSK,M取值分别为2,4,8;E表示信号的平均功率;Δθ为载波相位残差;n(k)为均值为0,方差为N0的复高斯白噪声。
OQPSK是在QPSK基础上发展起来的,相位只在0°和±90° 3种相位之间跳变,因此OQPSK码元可以表示为:
a(k)∈{ej2π(m-1)/4+Δφ,m=1,2,3,4,Δφ=0,±π/2}
(2)
对于π/4-QPSK,信号的相邻码元之间相位差为π/4,因此π/4-QPSK码元信号可以表示为:
a(k)∈{ej2π(m-1)/4,m=1,2,3,4}
(3)
a(k+1)∈{ej2π(m-1)/4+π/4,m=1,2,3,4}
(4)
2 特征提取和分类识别
2.1 高阶累积量
对于1个零均值的k阶平稳随机过程x(t),其k阶累积量定义[5]为:
Ckx(f1,f2,…,fk-1)=Cum(x(t),x(t+f1),…,
x(t+fk-1))
(5)
式中:Cum(·)表示求累积量。
定义x(t)的p阶混合矩[5]为:
Mpq=E{[xp-q(t)x*(t)q]}
(6)
因此,x(t)的二阶、四阶累积量[6]表示为:
(7)
根据式(5)~式(7),可知高斯白噪声的二阶以上的累积量恒定为0,因此计算BPSK、QPSK、OQPSK、π/4-QPSK和8PSK的四阶累积量理论值如表1所示。

表1 四阶累积量理论值
表中E表示接收信号的能量。
针对不同的调制样式,结合表1,特征向量F的理论值为:
(8)
因此,利用特征向量F,采用最小欧式距离准则建立分类判决器,分类判决器表示为:
(9)
通过该分类判决器,可以将BPSK、QPSK、OQPSK、π/4-QPSK、8PSK分为三大类:BPSK、{QPSK、OQPSK}、{π/4-QPSK、8PSK}。
2.2 差分星座最小环带模值方差
根据式(2)~式(4),可知QPSK和OQPSK、π/4-QPSK和8PSK星座分布相同。但是,事实上QPSK和OQPSK、π/4-QPSK和8PSK的相位跳变规律是不同的,因此QPSK和OQPSK、π/4-QPSK和8PSK信号差分运算后的星座图分布是有差异的。对式(1)的信号进行差分运算,得到:
Δy(k)=y(k+1)-y(k)=
(10)
式中:Δn(k)表示均值为0、方差为2N0的复高斯白噪声。
图1~图8为4种不同调制样式的信号星座图和差分重构星座图。

图1 QPSK调制星座图

图2 差分QPSK调制星座图
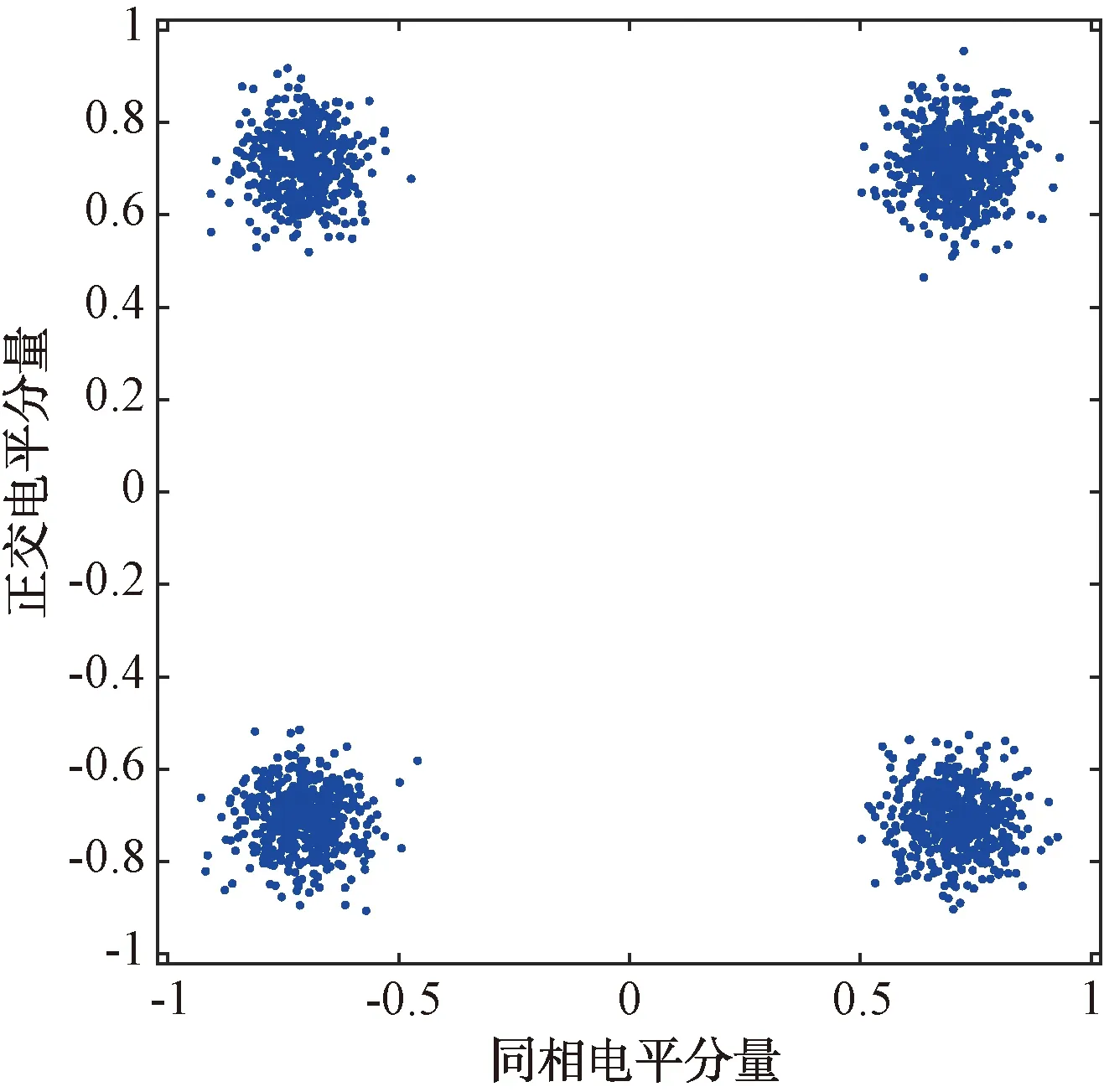
图3 OQPSK调制星座图
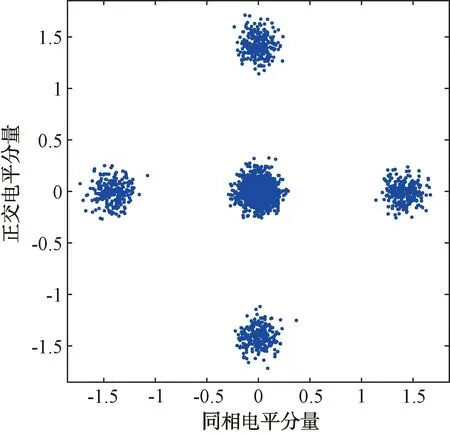
图4 差分OQPSK调制星座图

图5 π/4-QPSK调制星座图
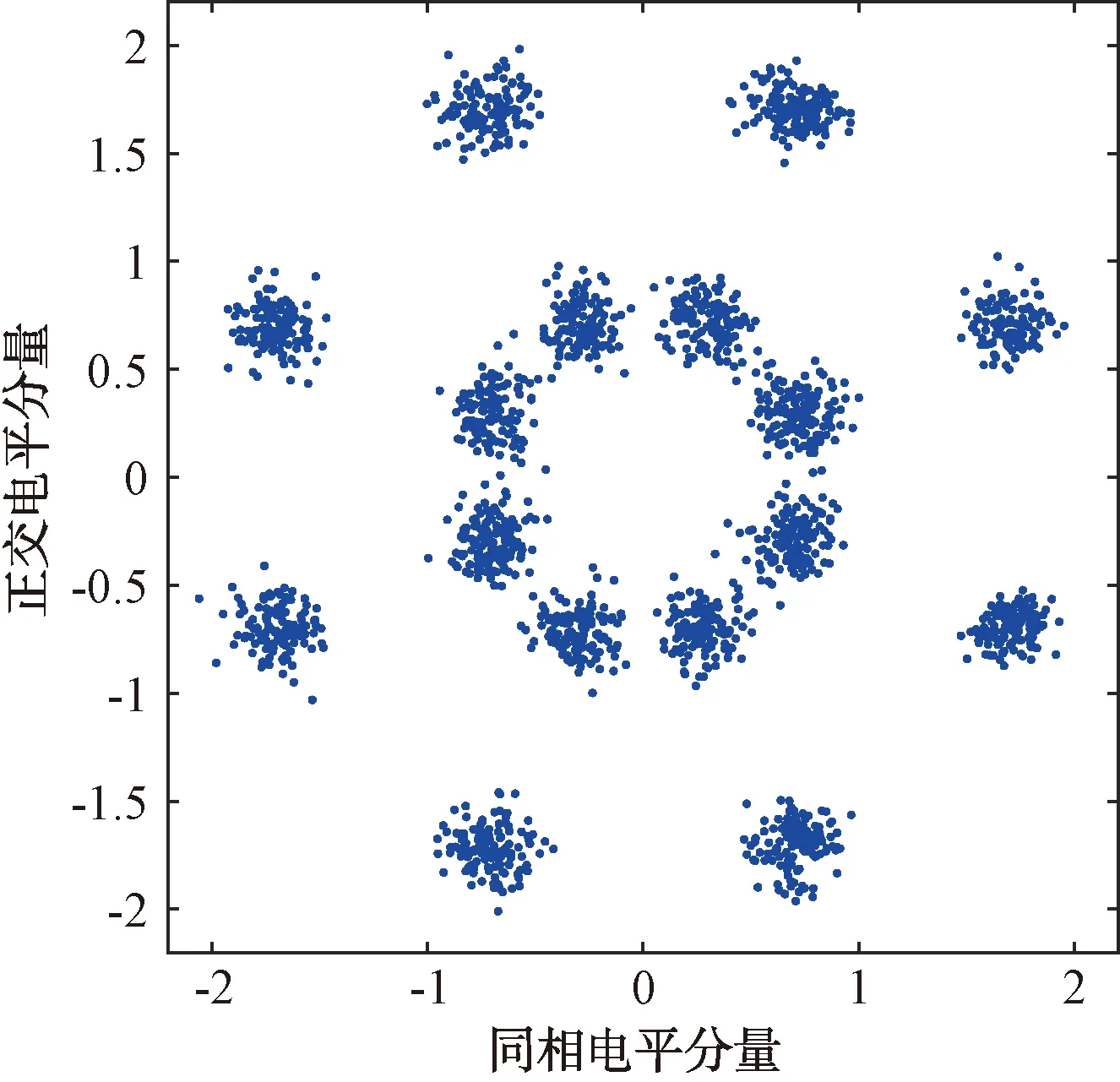
图6 差分π/4-QPSK调制星座图
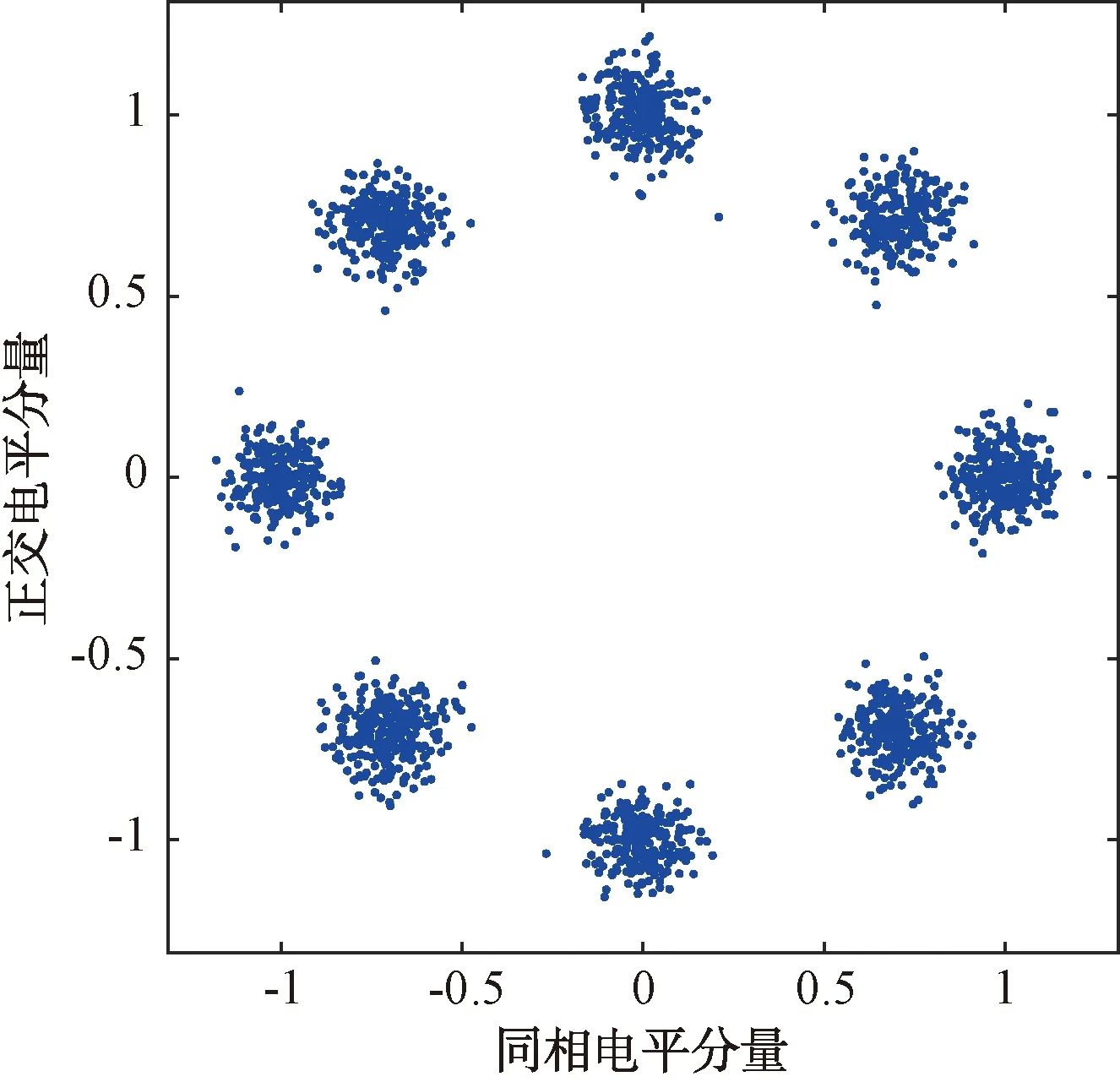
图7 PSK调制星座图

图8 差分8PSK调制星座图
根据式(2)、(3)、(4)、(10),差分星座分布规律如下:差分QPSK信号星座按照近似25%、50%、25%分布在内外3个环带上。差分OQPSK信号星座按照近似50%、50%分布在内外2个环带上。差分π/4-QPSK信号星座按照近似50%、50%分布在内外2个环带上。差分8PSK信号星座按照近似12.5%、25%、25%、25%、12.5%分布在内外5个环带上。如果星座点全部来自同一个环带,则模值方差比较小。反之,不同环带星座点的模值方差较大。已知距离星座图中心点越远的点,其模值分布越紧凑[7]。因此,越靠近星座图的外环带星座点越容易受噪声等因素干扰导致环带不清晰。针对QPSK、OQPSK、π/4-QPSK和8PSK信号,本文采用差分星座的最小环带模值方差作为特征进行分类识别。
首先,计算差分信号瞬时归一化幅值,表示为:
(11)
(12)
然后,瞬时归一化幅值排序,表示为:
S(k)=sort(Y(k))
(13)
式中:sort(*)表示升序排列运算;k=1,…,N。
最后,计算截断长度为L的S(k)方差,表示为:
Pr=var(S(k)),k=1,2,…,L
(14)
式中:var(*)表示方差运算;L≤N。
对于OQPSK,S(k)的前N/2数据来自最小环带;对于QPSK,S(k)的前N/2数据肯定来自不同的环带,因此方差必然偏大。同理,对于π/4-QPSK,S(k)的前N/2数据来自最小环带;对于8PSK,S(k)的前N/2数据肯定来自不同的环带,因此方差必然偏大。通过Pr和理论阈值比较,{QPSK、OQPSK}信号小于门限判定为OQPSK,否则为QPSK;{π/4-QPSK、8PSK}信号小于门限判定为π/4-QPSK,否则为8PSK。
对上述4种调制信号的星座点按照上述比例截断,得到模值方差的理论值如表2所示。

表2 各种信号不同截断长度模值方差理论值
由于受噪声、码间干扰以及有限长度截断等因素影响,实际应用中门限阈值稍微高于理论值。
2.3 分类识别流程
根据上述分析,BPSK、QPSK、OQPSK、π/4-QPSK、8PSK 5种调制信号的识别流程如下:

(2) 根据式(9)将调制信号分为三大类:BPSK、{QPSK、OQPSK}、{π/4-QPSK、8PSK}。
(3) 根据式(11)、(12)、(13)计算N点长度信号的升序瞬时归一化幅值,截断L=N/2计算结果,根据式(15)计算星座最小环带模值方差特征f3。对于{QPSK、OQPSK}子类信号,如果方差小于设定门限h1,则判定为OQPSK;否则,判定为QPSK。对于{π/4-QPSK、8PSK}子类信号,如果方差小于设定门限h2,则判定为π/4-QPSK;否则,判定为8PSK。
3 仿真分析
针对提出的BPSK、QPSK、OQPSK、π/4-QPSK、8PSK调制信号样式识别算法,本文采用MALTAB软件进行算法性能仿真验证。分别仿真了不同信号长度、不同信噪比和载波剩余相位下的信号调制样式识别性能。
(1) 不同信号长度下算法识别性能
设定信噪比为10 dB,载波剩余相位残差为0,信号长度N为400,600,800,1 000,1 200,1 400,1 600,1 800,2 000,2 200,判决门限h1=0.085,h2=0.05,每种信号2 000次识别,不同信号长度下算法的识别性能情况如图9所示。根据图9分析可知,随着信号长度N的增加,调制信号的识别准确率逐渐增加。当信号长度N达到1 600,几种调制信号识别率可以达到100%。

图9 不同信号长度下信号识别率情况
(2) 不同信噪比下算法识别性能
设定载波剩余相位残差为0,信号长度N=1 600,判决门限h1=0.085,h2=0.05,信噪比5~20,信噪比步径间隔为1,每种信号2 000次识别,不同信噪比下信号的识别性能如图10所示。根据图10可知,随着信噪比增加,信号的识别率逐渐增大,当信噪比等于10 dB时,几种调制信号的识别率可达到100%。

图10 不同信噪比下信号识别率情况
(3) 不同载波剩余相位下算法识别性能
设定载波剩余相位取{0、5°、15°、25°},信号长度N=1 600,判决门限h1=0.085,h2=0.05,信噪比5~20,信噪比步径间隔为1,每种信号2 000次识别,不同信噪比下信号的识别性能如图11所示。根据图11可知,该算法对于载波残余相位不敏感。
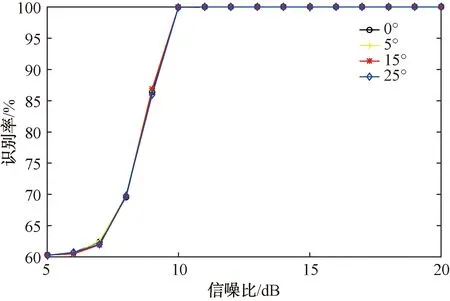
图11 不同载波残余相位下信号识别率情况
4 结束语
对于MPSK类内{BPSK、QPSK、OQPSK、π/4-QPSK、8PSK}这几种调制样式信号,本文提出了一种基于高阶累积量和差分星座最小环带模值方差进行信号调制样式识别的算法。首先利用四阶累积量将信号区分为BPSK、{QPSK、OQPSK}、{π/4-QPSK、8PSK}三大类,然后利用差分星座最小环带模值方差进一步将QPSK、OQPSK、π/4-QPSK、8PSK子类信号区分出来。通过仿真表明,当信噪比增加到10 dB,信号长度为1 600的情况,这5种信号的识别率可以达到100%。同时,仿真表明该识别算法对载波残余相位不敏感,算法的鲁棒性较好。
