基于Hilbert变换的高精度测频研究

何洋炎,王 林

(中国电子科技集团公司第五十一研究所,上海 201802)

0 引 言

20世纪50年代以来,瞬时测频技术应现代电子战的需求而诞生,主要分为模拟瞬时测频和数字瞬时测频2个方向。前者虽说工程上易于实现,但是稳定性差、易受各类因素的影响以及测频精度不高,故很少应用于工程设备中;后者则很好地克服了上述缺点。目前其主要有以下几种数字测频算法:(1)基于幅值的测频算法[1];(2)基于相位的测频算法[2];(3)基于频率信息的测频算法[3];(4)基于功率谱的测频算法[4]。上述各类算法各有优缺点,其中第(2)类相位法以其瞬时性好、测频精度优等特点而在工程上被广泛采用;但是在非合作辐射源及少采样点数时,所测目标频率精度往往难以满足目标运动特征提取的要求。基于此,本文提出了利用希尔伯特变换为参考信息,通过相位信息之间的相似性重构目标信息,从而提取出满足参测需求的超高精度频率。

1 理论基础及所提算法

1.1 瞬时频率[5]

瞬时频率的确定目前有多种不同的方式,目前比较公认的是Gaber所提出的利用解析信号以确定瞬时频率的数值。该方法主要是依托于希尔伯特变换,举例说明,对于信号a(t),构造其复数域的解析信号,其中H(f(t))表示对信号f(t)进行希尔伯特变换,如下式所示:

F(t)=a(t)+jH(a(t))

(1)

当得到信号的虚部后,即获得了信号的相位信息时,可以将信号写成如下的解析形式:

F(t)=B(t)ejθ

(2)

信号的瞬时频率一般被定义为相位对时间的一阶导数,这也符合物理意义上关于频率的概念,如下式所示:

(3)

以上所引出的关于瞬时频率的解算方式,作为后续所提方法的理论依据。

1.2 Hilbert变换

Hilbert变换具有诸多优良特性,常会利用其来构造解析信号,在此先介绍Hilbert变换,为后续所提方法中利用其相关特性奠定一定的基础。

对于实值函数a(t),t∈(-∞,∞),它的希尔伯特变换定义为a(t)与1/πt的卷积:

(4)

式中:符号*表示卷积。

利用卷积的特殊性质,即2个函数的卷积傅里叶变换等于2个函数傅里叶变换的乘积,设a(t)为原信号,F(a(t))表示对信号进行傅里叶变换,H[f(t)]为对信号进行希尔伯特变换,于是可得:

(5)

利用欧拉公式ejθ=cosθ+isinθ,可以得到:

(6)

式中:sgn(f)为符号函数,定义为:

(7)

通过上述变化的分析,可以看出,所谓希尔伯特变换就是一个相移转换器,对于正频率成分,将相位移动了-π/2; 反之负频率成分,移动了π/2。同时,可以发现复数域信号在实数域的投影就是时域信号,于是利用Hilbert变换,就可以得到含有信号相位变化信息的复数表达式。

1.3 正交性分析

由前两节的分析,理论上的Hilbert是基于无限时间长度的,但是此需求在实际工程应用中难以满足,甚至在绝大多数条件下,只具备少量点数的用于信号相位信息的求取,受限于工程应用的局限,势必对虚部信号的准确获得造成一定程度的误差,主要体现在其与原始实部信号的正交性上,正交度定义如下:

(8)

式中:η表示正交度;M表示量化位数;D(·)表示模数量化;H(·)表示Hilbert变换。

现给出如下仿真条件,分析测频误差与正交度之间的关系(具体参数参见表1),分别给出采样点数与测频误差的关系曲线,以及采样点数与正交度的关系曲线,如图1所示。

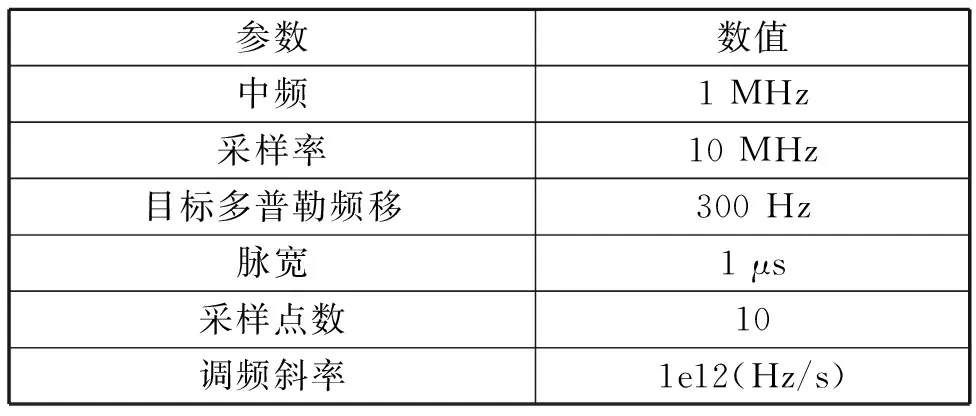
表1 基本参数

图1 测频误差、正交度随采样点数的变化

从图1(a)中可以看出,误差随着采样点数的增加呈现整体下降的趋势。这是由于随着采样点数的增加,在频率域中对信号处理过程中原始信号的信息保存就越完整,恢复至时域中时,对应的幅相信息就更准确。同样,观察图1(b)中正交度的变化趋势,可以看出随着采样点数的增加,正交度的数值不断趋于0,意味着信号实部与Hilbert变换所得虚部之间的正交度越高,复原的信号越接近真实信号。对比图1(a)与(b),可以发现测频误差与正交度之间呈现出相同的变化趋势,基于此,可以考虑利用提高信号的正交度来满足高要求的测频需求。

1.4 基于信号相似性的频率测量

从上述分析可以得到,为了提高测频精度,满足目标运动特征表达的需求,需得到更加贴合实际信号的复信号形式,即与实部正交性更好的信号虚部信息。但是单纯地基于Hilbert变换得到的测频精度(特别是在少量采样点时)难以满足实际测频的要求,提高信号虚部的准确度主要解决2个方面问题:(1)虚部的符号问题;(2)虚部的绝对值。其中,第1点可以通过Hilbert变换获得,通过前述分析信号的取值不存在跳变点,则Hilbert变换得到的数值正负是符合实际情况的;第2点,考虑到变换所得信号的幅度会呈现出起伏状态,即偏离真实幅度,且均值也会因为点数及采样率的原因,并非与实际幅值相近。现考虑基于分析不同信号的特征,利用相似性原理来确定信号的幅值。

1.4.1 点频信号

如果是单一频点的信号,那么在等间隔采样点之间,理论上信号的相位变化值应该是相同的,如下式所示:

mod(Δφ1,2π)=mod(Δφ2,2π)=…=

mod(ΔφN-1,2π)

(9)

式中:mod()表示取余;Δφi表示相邻采样点之间的相位差;N表示采样点数。

现考虑以一定的步进遍历幅值变化区间,求取各幅值点处基于相似性原理的相差抖动情况,典型的相似性处理方式(皮尔逊相似系数)如下式所示[6]:

(10)

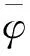
该处理方式存在相位跳变问题,且工程运算量较大,现拟采用如下相关系数的计算方法:

(11)

1.4.2 线性调频信号

给出调频信号的模型如下式所示:

(12)

式中:K表示调频斜率;φ0表示初相位。

于是可以得到图2。

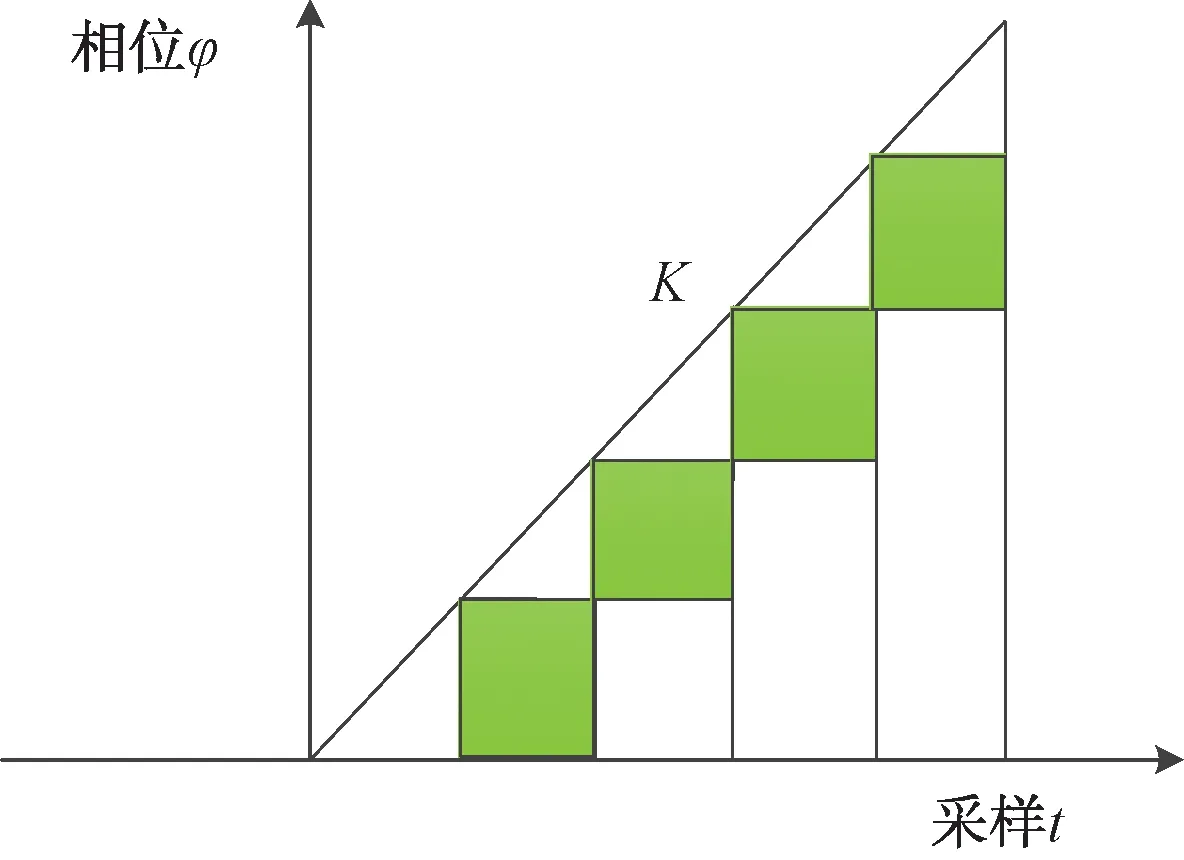
图2 线性调频信号相位差差值变化

图2中的灰区块代表相邻采样点相位的差值,通过相位差差值的运算可以得到如图2所示的结果。相差的差值也呈现出恒值的态势,因此同样可以采样类似上节的分析,利用相同的相关系数计算方法得到不同幅值对应的相位抖动情况,分析过后则可以将2类典型信号采取相同的信号处理方式进行预处理,在保证算法能够处理不同类型信号的同时,节省了工程应用中的资源消耗。

接着给出了2类信号的相似度曲线,如图3所示。

图3 2类信号的相似度曲线

从图3中可以清楚地看到,2条不规则曲线均存在极小值点(即所需的幅值点),为后续的超精度测频提供了理论保证。

2 仿真分析

根据实际需求,给出如表1所示的基本参数设置。

基于上述参数给出了基于所提算法与常规瞬时测频算法的比较,测频误差如图4所示。

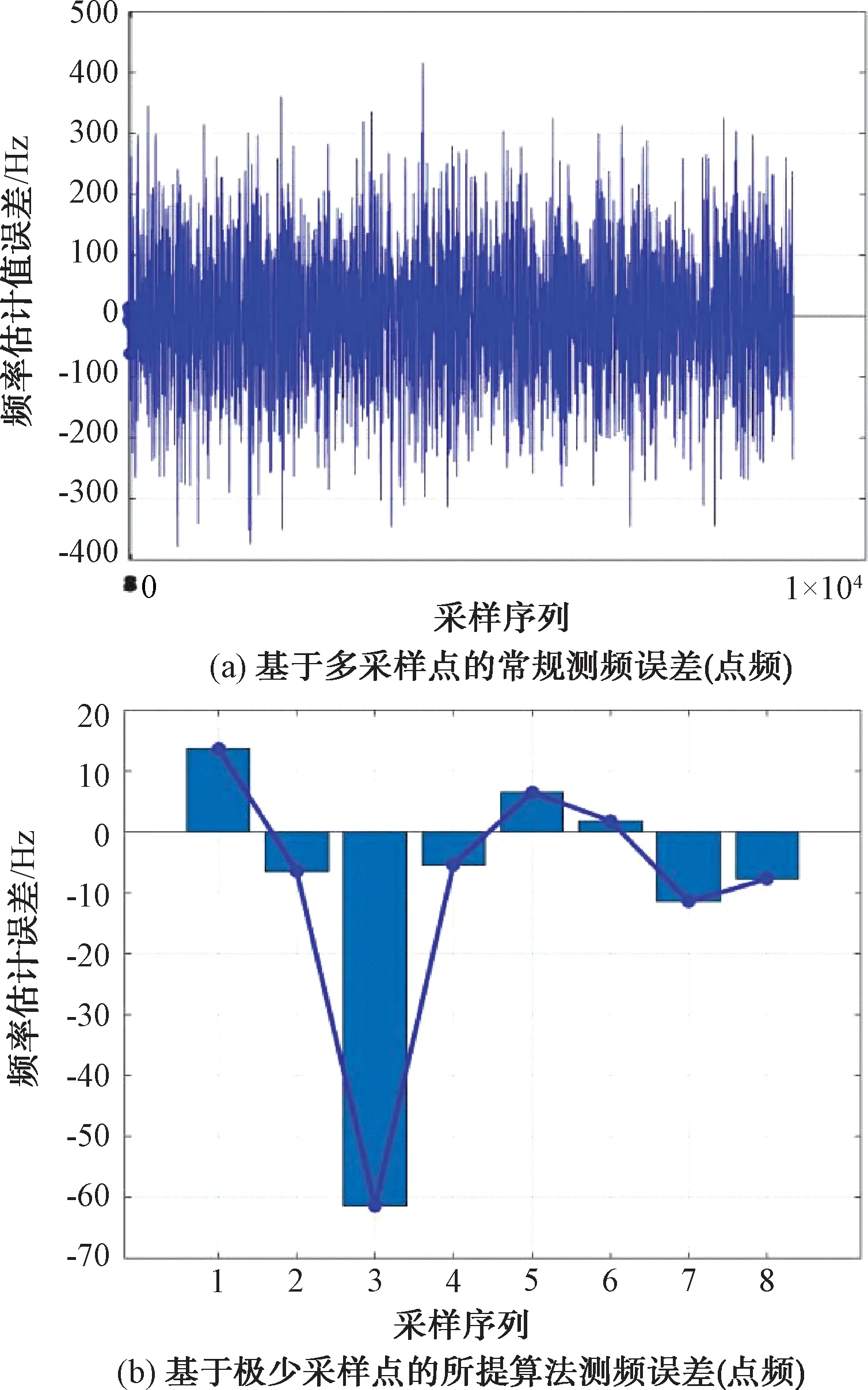
图4 基于所提算法与常规瞬时测频算法的测频误差比较

从图4中可以清晰地看出,常规方法下即便是能够连续获取上万采样点,测频精度也只能达到300 Hz的精度要求,对于测量目标百赫兹量级的测频需求是难以满足的;然而采用了基于所提相似算法,仅利用不到10个采样点,得到测频精度可以控制在60 Hz以内,平均数值可控制在10 Hz上下,可以很好地满足实际测频的需求。接着,基于所提方法给出了线性调频信号的关键参数调频斜率的测量结果,如表2所示。

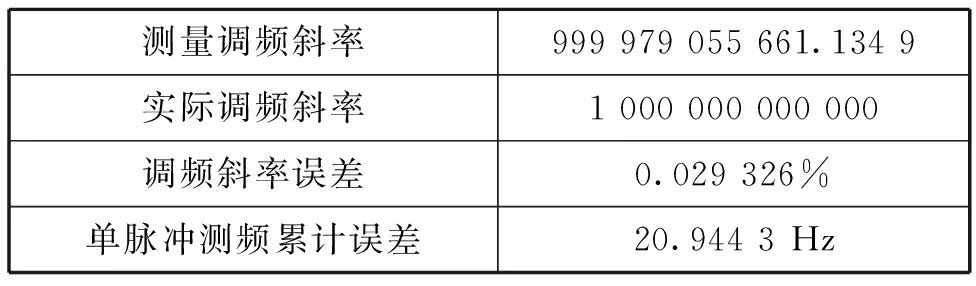
表2 参数测量结果

从上述结果可以看出,所提算法不但能够很好地测得点频信号的频率,同时对于线性调频信号调频斜率的测量误差低于千分之一,累计测频误差单脉冲小于21 Hz,能满足实际测量百赫兹量级多普勒频率的需求。

3 结束语

本文通过分析不同采样点测频误差与信号实部虚部之间正交性的变化趋势,引出了在低采样点需提高信号的正交性作为提升测频精度的基础;而后通过分析相位信息的相似性,采用了更符合工程实现的相似性处理函数,通过极值点的求取重构目标信号,进而求得相应的精准频率。仿真结果也证明了所提算法在不同信号类型上的适用性与超精度性能。