一种改进抽样函数自适应滤波的抗灵巧噪声干扰方法

闵柏成,张世超,陈凯翔,邱硕丰

(中国船舶集团有限公司第八研究院,江苏 扬州 225101)

0 引 言

近年来,随着脉冲压缩技术的发展,现代机载雷达的抗干扰能力大大提高,传统噪声干扰对脉冲压缩雷达的干扰能力大幅下降。针对此问题,国内外学者对灵巧噪声干扰[1]这种新型干扰颇为重视。针对脉冲压缩雷达信号处理的特点,灵巧噪声干扰由干扰机截获的雷达发射信号和本地噪声调制而成,这样在提高了传统噪声干扰相参性的同时,也将噪声能量集中起来,从而对脉冲压缩雷达造成了压制性和欺骗性双重干扰效果。

线性调频(LFM)脉冲压缩体制的机载雷达在灵巧噪声干扰环境中,干扰对目标回波形成极好的压制性和欺骗性干扰效果[2],导致常规的抗干扰措施无法在时域及频域分离干扰和目标回波。针对此问题,目前已有多种灵巧噪声干扰的抑制方法。文献[3]通过对噪声和脉冲卷积2种灵巧干扰方式的干扰效果进行分析,给出了一种特殊的波形设计。该波形结合了参数捷变和低截获二者的理念,达到了一定的抗干扰效果。文献[4]从宏观角度介绍了灵巧干扰的概念、发展过程、分类,通过干扰的作用机理和干扰效果,概括并分析了灵巧噪声干扰的抑制方法。文献[5]通过对灵巧噪声干扰的假目标数量与卷积噪声干扰的信号时宽进行分析,其仿真结果表明二者成正比关系。文献[6]通过自适应旁瓣对消系统可有效抑制灵巧噪声干扰。以上文献均对线性调频脉冲压缩体制的机载雷达抗灵巧噪声干扰提供了参考,但其研究重点基本保持在灵巧干扰本身的干扰效果及干扰调制方式上,针对线性调频信号雷达本身的抗干扰效果并不明显,且这些方法都有一定的局限性,不具有普适性。

针对灵巧噪声干扰对脉冲压缩雷达造成的压制性和欺骗性双重干扰效果的问题,本文首先通过差拍处理,使信号和干扰在频域实现解耦分离,然后采用改进抽样函数的变步长滤波算法,滤除解耦后的回波信号分量,最后对消解耦前后的干扰分量,通过逆差拍处理方式恢复目标回波信号。利用本文所提的方法可有效地抑制灵巧噪声干扰,无需对干扰进行参数估计,并能较好地恢复目标回波。

1 信号和干扰模型

LFM脉冲压缩体制的机载雷达具有较高的速度测量精度和速度分辨力,其发射信号通常具有较长的时宽与较大的带宽。同时,灵巧噪声干扰作为一种新型干扰方式,与LFM雷达的目标回波具有很多相似之处,因此对目标回波信号具有很强的欺骗性。此外,在这种新型干扰方式下,目标回波信号的带内集中了能量较强的干扰信号,从而压制目标回波[7]。

设第m个脉冲重复周期雷达发射信号为:

(1)

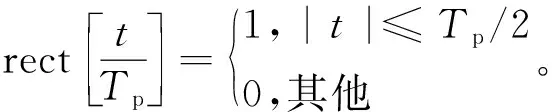
此时,雷达的回波信号为:

sR(t,m)=a(m)sm′(t-τ(m))

(2)

(3)

式中:a(m)表示目标回波的幅度;τ(m)表示目标回波的时延;fd(m)为目标回波的多普勒频移。

目前,应用较广泛的灵巧噪声干扰是通过干扰机截获的雷达发射信号与本地噪声卷积调制而成[7],为达到更好的欺骗干扰效果,对卷积噪声干扰进行移频处理,通过改变移频量形成具有压制效果的假目标干扰,使真实的目标回波在时域及频域完全被淹没在干扰中。

根据式(1)及灵巧噪声的产生方法,第m个脉冲重复周期经移频后的卷积噪声干扰如下:

(4)

式中:b(m)表示第m个脉冲重复周期灵巧噪声干扰的幅度;τj(m)表示第m个脉冲重复周期灵巧噪声干扰的时延;fyp为移频量;n(t)为视频噪声信号。

2 灵巧噪声干扰抑制算法

根据目标回波和灵巧噪声干扰的时域匹配接收、频谱特性等,提取干扰特征[8],识别出灵巧噪声干扰后,通过抗干扰算法对灵巧噪声干扰进行处理。

2.1 差拍处理

假设干扰机截获第m个脉冲重复周期中的雷达信号,干扰机对该信号进行移频处理后进行卷积调制,并在该重复周期内与雷达目标回波一起进入雷达接收机,此时雷达接收信号如下:

Xm(t)=sR(t,m)+Jm(t)

(5)

由于雷达发射信号在第(m-1)个周期中未被截获,因此在该周期内雷达接收机中仅包含雷达目标回波。此时,利用第m和(m-1)个脉冲重复周期中的接收信号进行差拍处理[9],具体计算过程如下:

(6)

A={[fd(m-1)-fd(m)]+k[τ(m-1)-τ(m)]}t+[τ(m-1)-τ(m)]f0+

(7)

B=f0(t-τ(m-1))+k(t-τ(m-1))2/2

(8)

C=f0(t-τj(m))+k(t-τj(m))2/2+fypt

(9)

根据式(7)中A可知,雷达目标回波经差拍处理后变成单载频信号,其信号频率为:

ft=[fd(m-1)-fd(m)]+

k[τ(m-1)-τ(m)]

(10)

式中:第1项可通过目标加速度、脉冲重复频率及光速表示:

fd(l)-fd(l+1)=-2a/(cfp)

(11)

通常情况下,目标加速度远小于光速与脉冲重复频率的乘积,使fd(l)-fd(l+1)≈0。相对于同一目标而言,LFM机载雷达相邻脉冲重复周期的时延差很小,使τ(m-1)-τ(m)≈0。因此,ft≈0。

根据式(8)、(9)中B和C可知,灵巧噪声干扰经差拍处理后未消去与时间t相关的二次项,其干扰信号形式仍为经一定移频处理的噪声卷积干扰。此时分为以下2种情况:

(1) 当移频量fyp=0时,灵巧噪声干扰的中心频率由第m-1个脉冲重复周期的目标时延τ(m-1)和第m个脉冲重复周期的干扰时延τj(m)共同决定,如果|k[τj(m)-τ(m-1)]|的值大于干扰带宽的一半,此时差拍处理后的目标回波与灵巧噪声干扰可在频域上基本实现完全分离。此时,任意选取低通滤波器即可实现目标与干扰的分离,通过对消实现灵巧噪声干扰的抑制。

(2) 当移频量fyp≠0或|k[τj(m)-τ(m-1)]|的值小于干扰带宽的一半时,前者通过改变移频量使灵巧噪声干扰对目标回波产生压制效果,后者是由于目标回波落入了灵巧噪声干扰的信号带宽内,此时,传统的滤波方法无法有效实现对回波信号的滤波,干扰对消效果下降。因此,本文采用改进抽样函数自适应滤波方法实现干扰对消。

2.2 改进抽样函数自适应滤波器原理

信号经差分处理后,目标回波信号ft位于接近于零的低频处,结合自适应陷波器的基本原理,对差分处理后的回波信号进行陷波处理,进而通过干扰对消的方式抑制灵巧噪声干扰,最终通过逆差拍处理恢复目标回波。

传统的自适应陷波原理框图如图1所示。

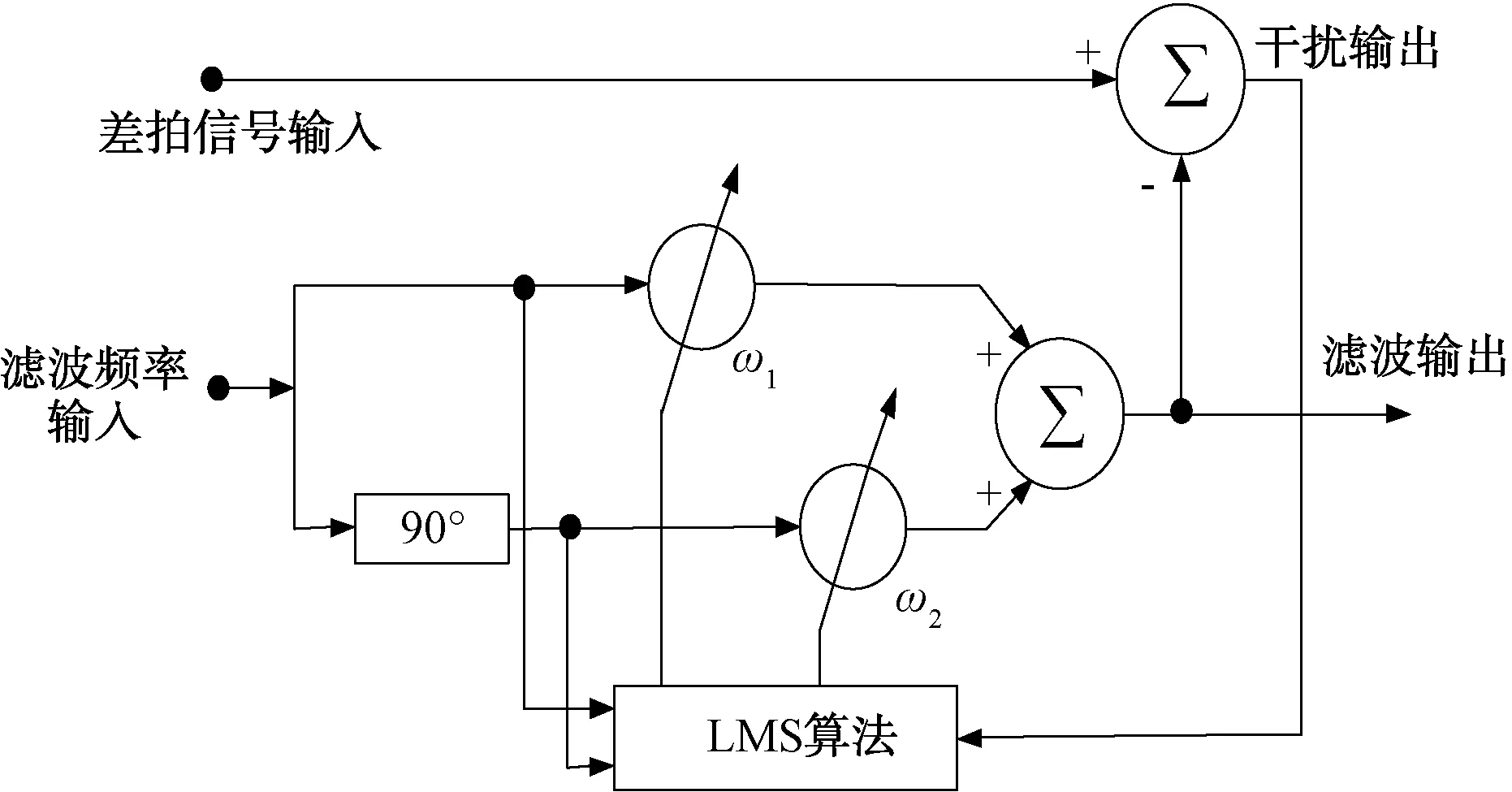
图1 传统自适应陷波原理框图

由图1可知,差拍信号输入为经差拍处理后目标回波分量及干扰分量的混合信号,滤波输入频率为f0的正弦信号。

由差拍信号输入到干扰输出的自适应冲激相应函数为:

(12)

式中:f0为需要进行滤波的频率值;μ为自适应滤波器的步长;a为滤波频率输入的信号幅值。

由于差拍处理后目标回波信号ft≈0,则令滤波频率输入f0=0,代入式(12)得:

(13)

通过式(13)可以看出,陷波器在单位圆内存在零点和极值点各一个,分别落在z=1和2μa2处。此时,在(0,ln(2μa2)/2π)区间范围内,可滤除ln(2μa2)/2π带宽内的频谱,该带宽的大小由自适应步长μ决定。

为实现灵巧噪声干扰的有效抑制,本文采用的改进抽样函数自适应LMS算法[10]如下:

e(n)=d(n)-cT(n)ω(n)

(14)

(15)

ω(n+1)=ω(n)+2μ(n)e(n)c(n)

(16)

式中:e(n)为n次迭代后的陷波输出信号;d(n)为n次迭代后的干扰对消信号;c(n)为第n次迭代时的滤波函数输入;ω(n)为第n次迭代时的加权;α为幅值调整系数;β为波形控制系数。

根据式(15)可知,改进抽样函数将抽样函数中心值进行翻转,并通过α、β的取值保证函数曲线[11]。由图2可以看出,改进抽样函数曲线中的步长与误差之间的对应关系,通过幅值调整系数α可控制陷波带宽,通过波形控制系数β控制函数的收敛速度。

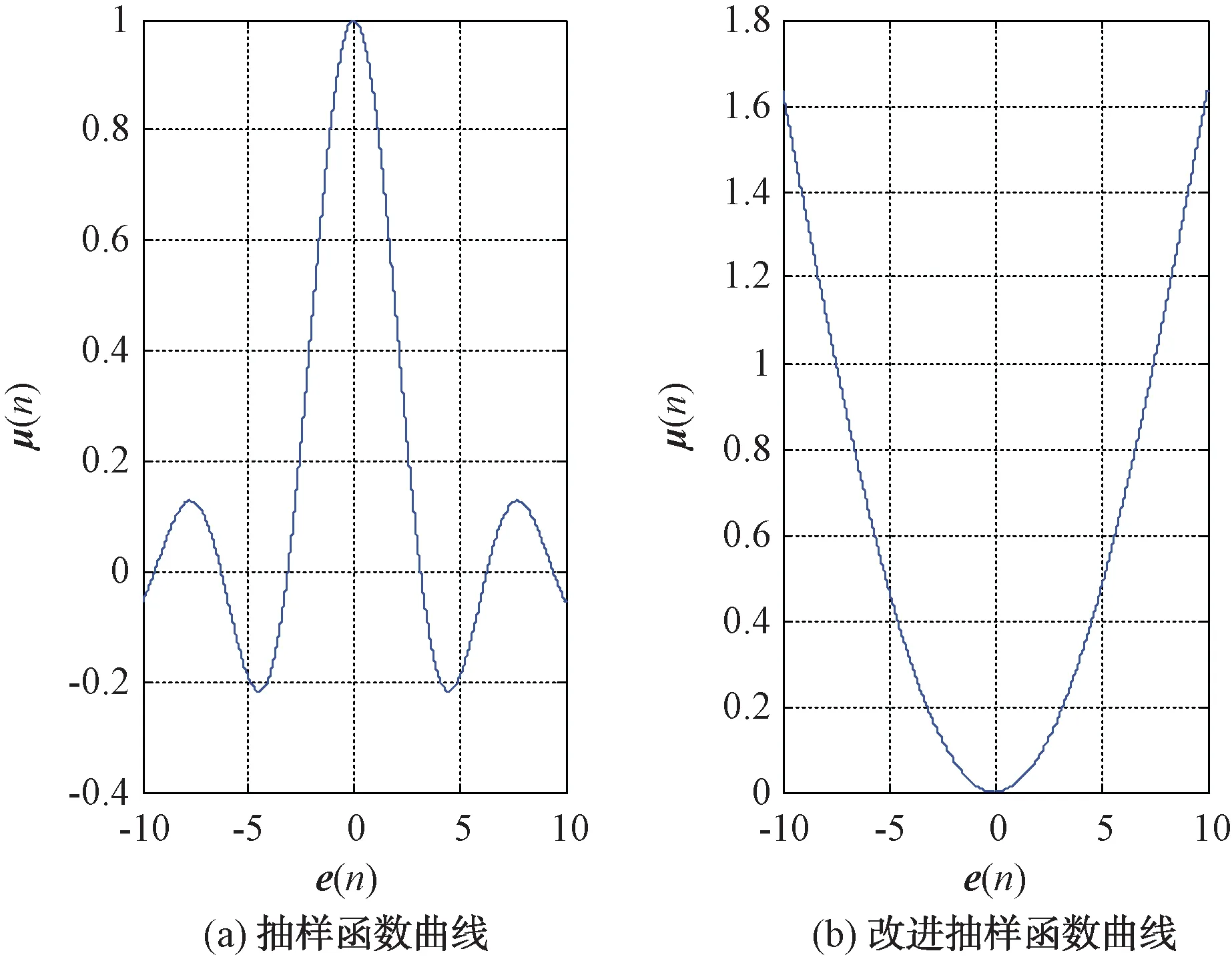
图2 抽样函数改进前后曲线对比

由于自适应陷波算法中,步长μ的大小决定了陷波带宽,通过合理的步长曲线可使陷波效果达到最优,针对2.1节中经差拍处理后目标回波分量及灵巧噪声干扰分量的耦合情况来选取α、β的取值可使陷波效果更优,并能有效对消干扰分量。

幅值调整系数α和波形控制系数β对步长曲线的影响如图3所示。由图3可以看出,通过控制β值改变步长的变化率,步长变化率即β的取值越小,步长变化越慢,此时陷波器的陷波效果主要取决于α的取值。当幅值调整系数α取值较大时,由于β取值相对较小,陷波器的陷波带宽较大,且在算法整个迭代过程中,更多情况处于较大陷波带宽中,此情况适用于灵巧噪声干扰的移频调制量fyp=0,且|k[τj(m)-τ(m-1)]|大于干扰带宽的一半。通过大且变化较慢的陷波带宽可更有效地滤除回波信号,干扰对消效果更加明显。

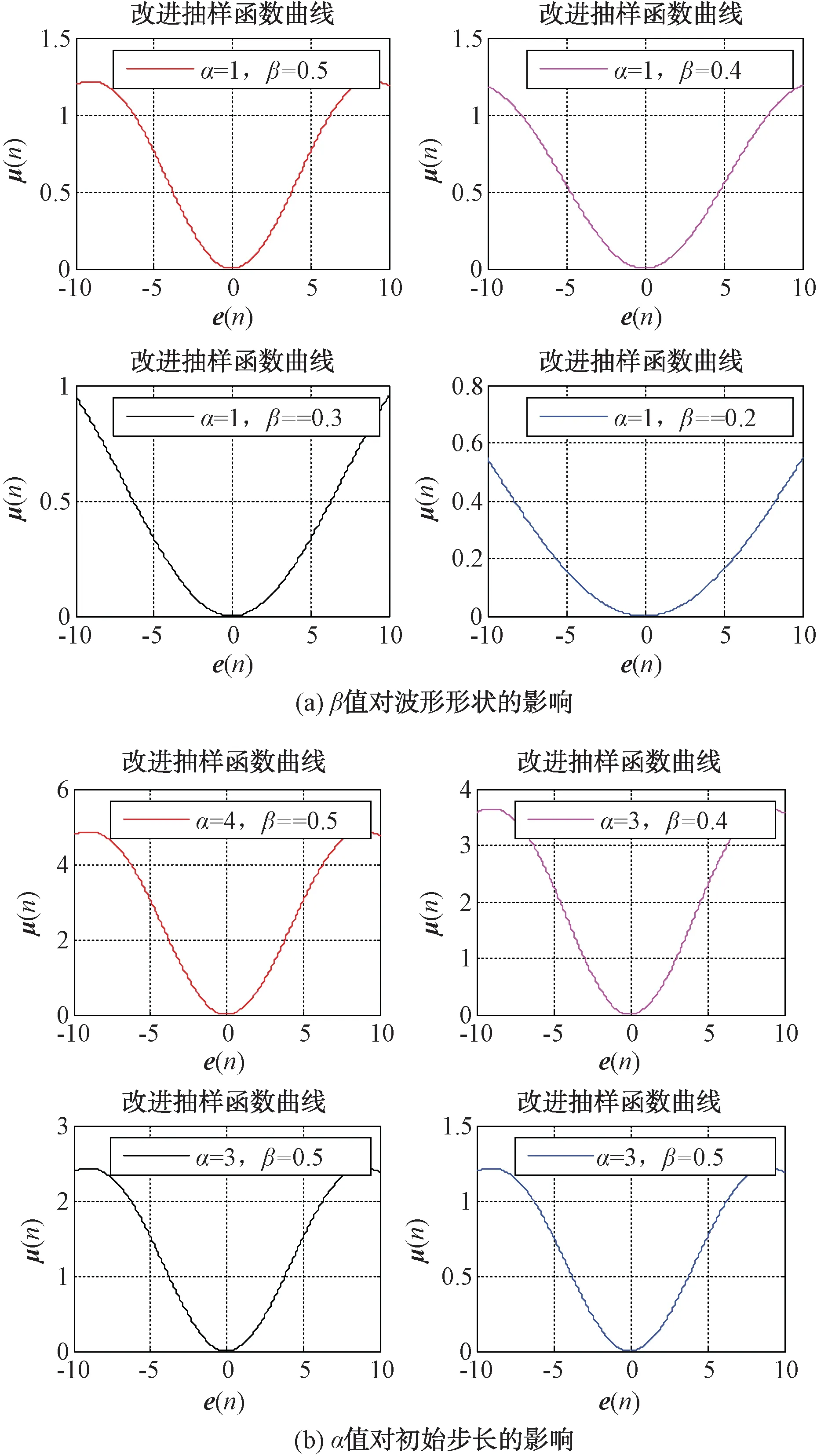
图3 2个系数对步长曲线的影响

当移频量fyp≠0或|k[τj(m)-τ(m-1)]|的值小于干扰带宽的一半时,干扰信号与目标回波经差拍处理后仍存在部分耦合。此时,通过较小的初始步长和较大的步长变化率(即α取值较小,β取值较大)可更有效地滤除目标回波并对消灵巧噪声干扰。

2.3 抗灵巧噪声干扰的算法流程

本文所提的抗灵巧噪声干扰的算法流程如图4所示,可分为4个步骤:

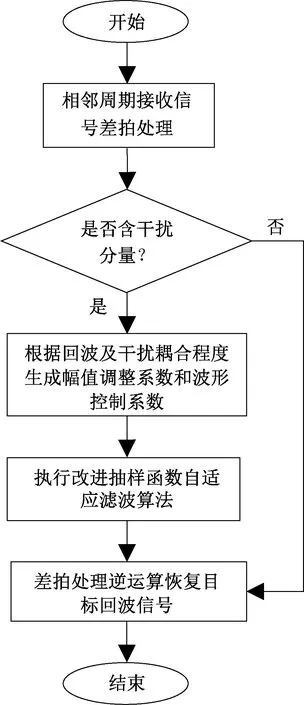
图4 抗灵巧噪声干扰的算法流程图

步骤1,根据式(6)对雷达接收机中相邻2个周期的接收信号做差拍处理,使真实目标回波信号消除二次项。

步骤2,根据差拍处理后的信号频谱,判断真实目标回波信号与灵巧噪声干扰信号的耦合程度,生成改进抽样函数的幅值调整系数α和波形控制系数β。

步骤3,通过式(14)～(16)完成差拍处理后灵巧噪声干扰分量的对消。

步骤4,通过差拍处理的逆运算恢复目标回波信号。

3 仿真验证及分析

3.1 算法流程仿真

仿真参数设置为:LFM雷达信号的中心频率f0=50 MHz,带宽B=100 MHz,脉冲宽度τPW=50 μs,脉冲重复周期为500 μs,线性调频信号的斜率k=BτPW。根据2.1节的分析,移频量、回波时延和干扰时延的设置分以下2种情况:

情况1:当移频量fyp=0且|k[τj(m)-τ(m-1)]|的值大于干扰带宽Bj一半的情况时,取τi(1)=80 μs,τj(2)=110 μs。

情况2:当移频量fyp≠0或|k[τj(m)-τ(m-1)]|的值小于干扰带宽Bj一半的情况时,取τi(1)=80 μs,τj(2)=90 μs,fyp=2 MHz。

图5(a)和图5(b)分别为无干扰条件下LFM信号的时域波形和幅频图;图5(c)和图5(d)分别为基于情况1和情况2参数设置的情况下,LFM回波信号受灵巧噪声干扰的幅频图。可以看出,2种情况下LFM目标回波信号的频谱成分完全被灵巧噪声干扰所淹没,无法通过当前频谱信息提取有用信息。图5(e)和图5(f)分别表示在有无干扰情况下信号的匹配滤波输出结果。可以看出,存在干扰的目标回波经匹配输出后,干扰和目标同时获得处理增益,LFM目标回波信号经脉压处理后被灵巧噪声干扰压制。因此,LFM回波信号与灵巧噪声干扰在时域及频域上完全耦合。

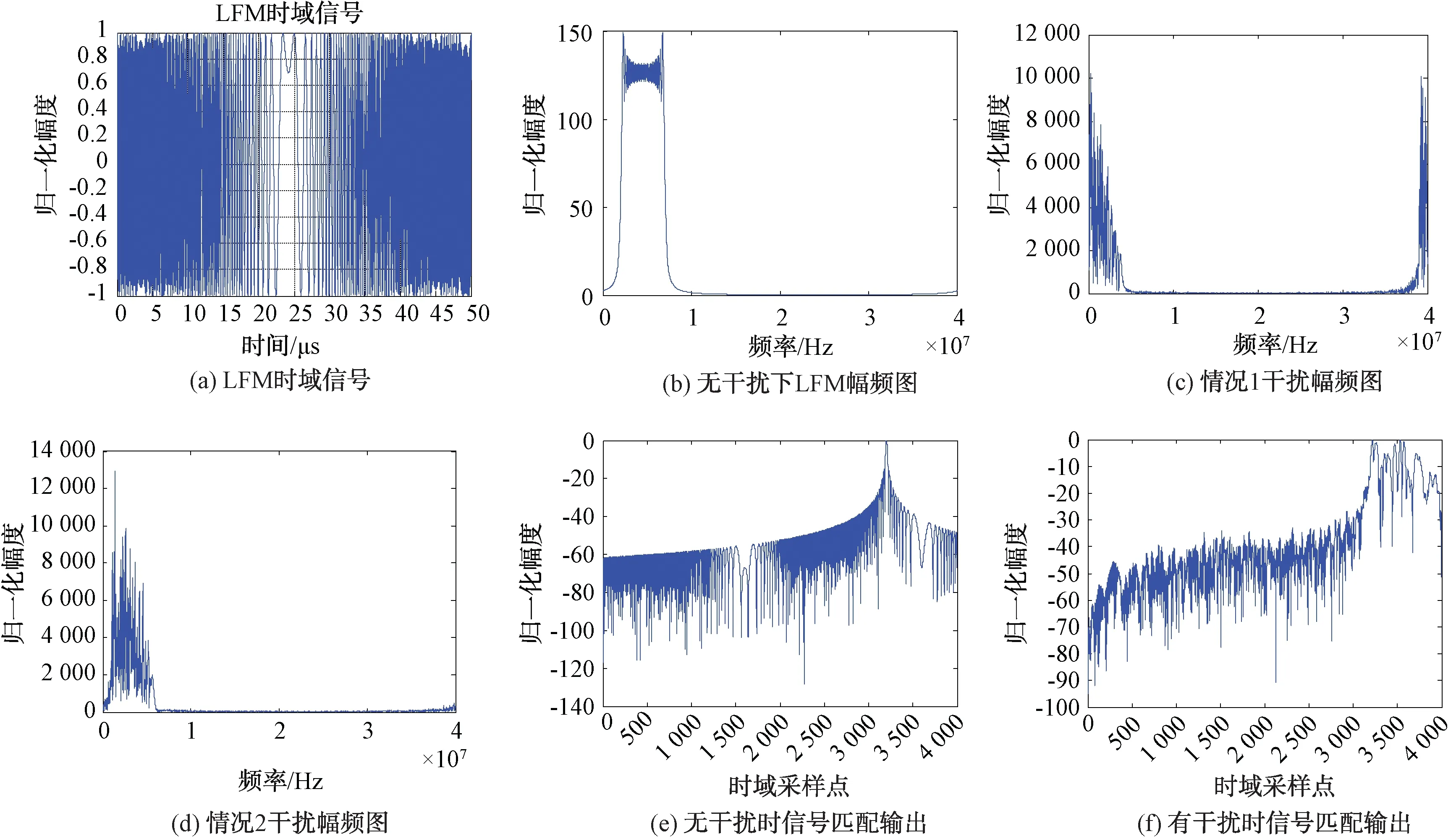
图5 LFM回波在有无灵巧噪声目标干扰下的对比仿真图

根据本文所提的算法,首先对2种干扰情况下的混合信号进行差拍处理。图6(a)为回波时延τi(1)=80 μs,干扰时延τj(2)=110 μs时混合信号经差拍处理后的幅频图。图6(b)为回波时延τi(1)=80 μs,干扰时延τj(2)=110 μs,fyp=2 MHz时混合信号经差拍处理后的幅频图。可以看出,经差拍处理后,LFM的目标回波分量与灵巧噪声干扰分量实现了在频域上的分离。相比于第2种情况,差拍处理在情况1干扰条件下目标回波与干扰的分离效果更好。然后根据2种情况干扰与回波信号的分离效果,在情况1干扰的条件下,设置滤波器中的幅值调整系数α=4和波形控制系数β=0.5,经滤波及干扰对消后信号的幅频图如6(c)所示。在情况2干扰的条件下,设置滤波器中的幅值调整系数α=1和波形控制系数β=0.2,经滤波及干扰对消后信号的幅频图如6(e)所示。最后对滤波对消后的信号进行逆差拍处理,2种情况下目标回波的恢复情况如图6(d)和6(f)所示。通过图6(c)～6(f)可知,经本文所提的改进抽样函数自适应滤波器后,可有效对消2种情况的干扰分量。与图5(b)中LFM幅频图相比,可根据幅值调整系数和波形控制系数实现有效滤波,并能良好地恢复LFM目标回波信号。

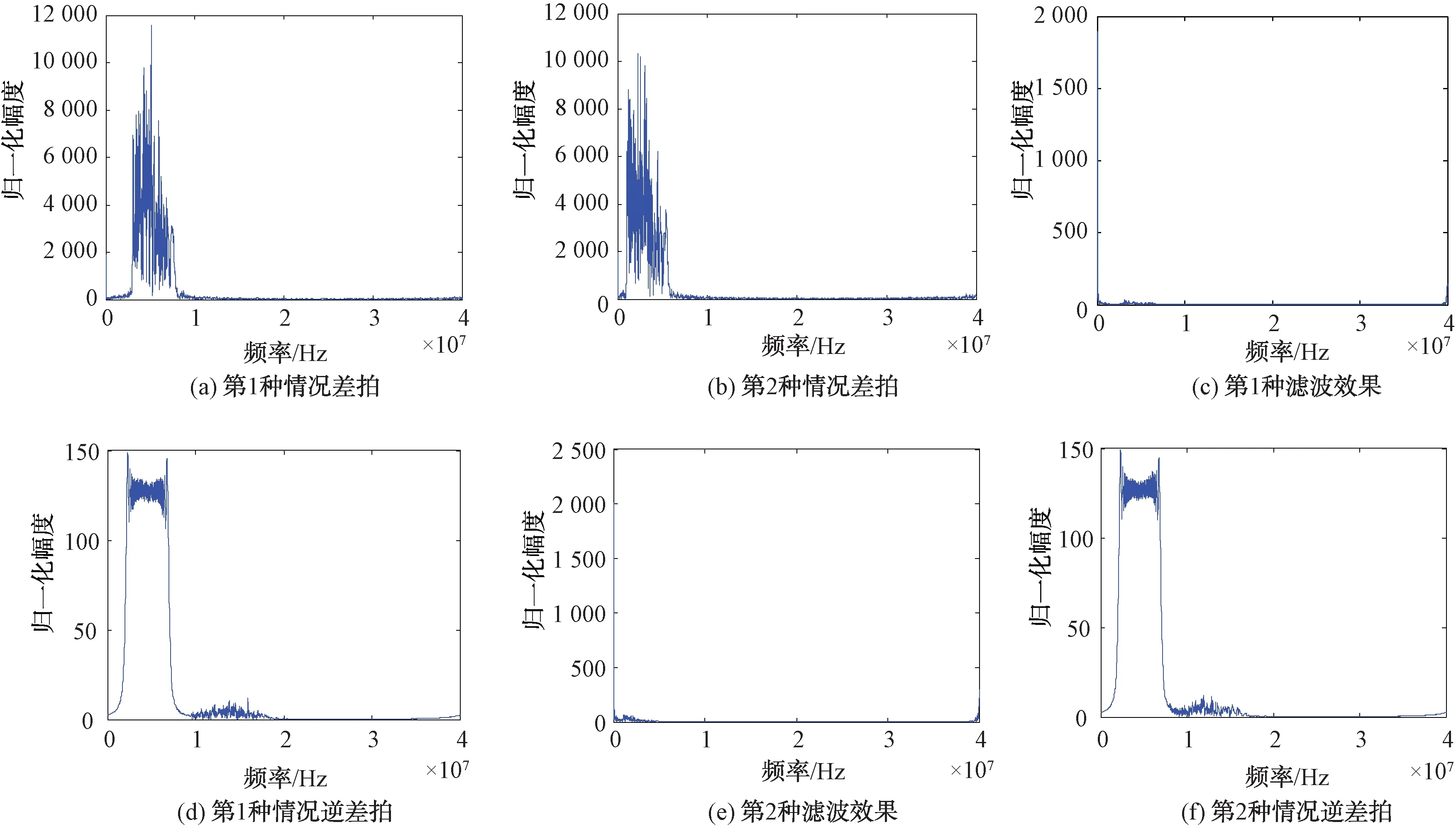
图6 抗灵巧噪声干扰前后对比仿真图

3.2 干扰抑制结果及分析

针对第1种情况下的干扰,通过改变幅值调整系数α的值来分析本文所提方法的干扰抑制性能。其参数设置如下:算法处理前目标回波与灵巧噪声干扰的初始信干比为δSJR=-10 dB,β=0.5,α=1,2,3,4,算法迭代次数N=2 000,其它参数设置情况与3.1节保持一致。经100次Monte Carlo实验[12],得到算法处理前后的信干比变化随迭代次数的变化情况如图7所示。由图7可以看出,随着幅值调整系数α的增大,其算法处理后干扰抑制效果更加明显。相比于普通抽样函数的幅值调整系数α=1时,滤波后的信干比提高了25 dB左右。因此,采用本文所提的改进抽样函数自适应滤波方法,在移频量fyp=0且|k[τj(m)-τ(m-1)]|的值大于干扰带宽Bj的一半时,可有效抑制灵巧噪声干扰。相比于定步长自适应滤波算法,干扰抑制后信干比至少提高10 dB,通过改变幅值调整系数α,可使信干比提高30 dB以上。

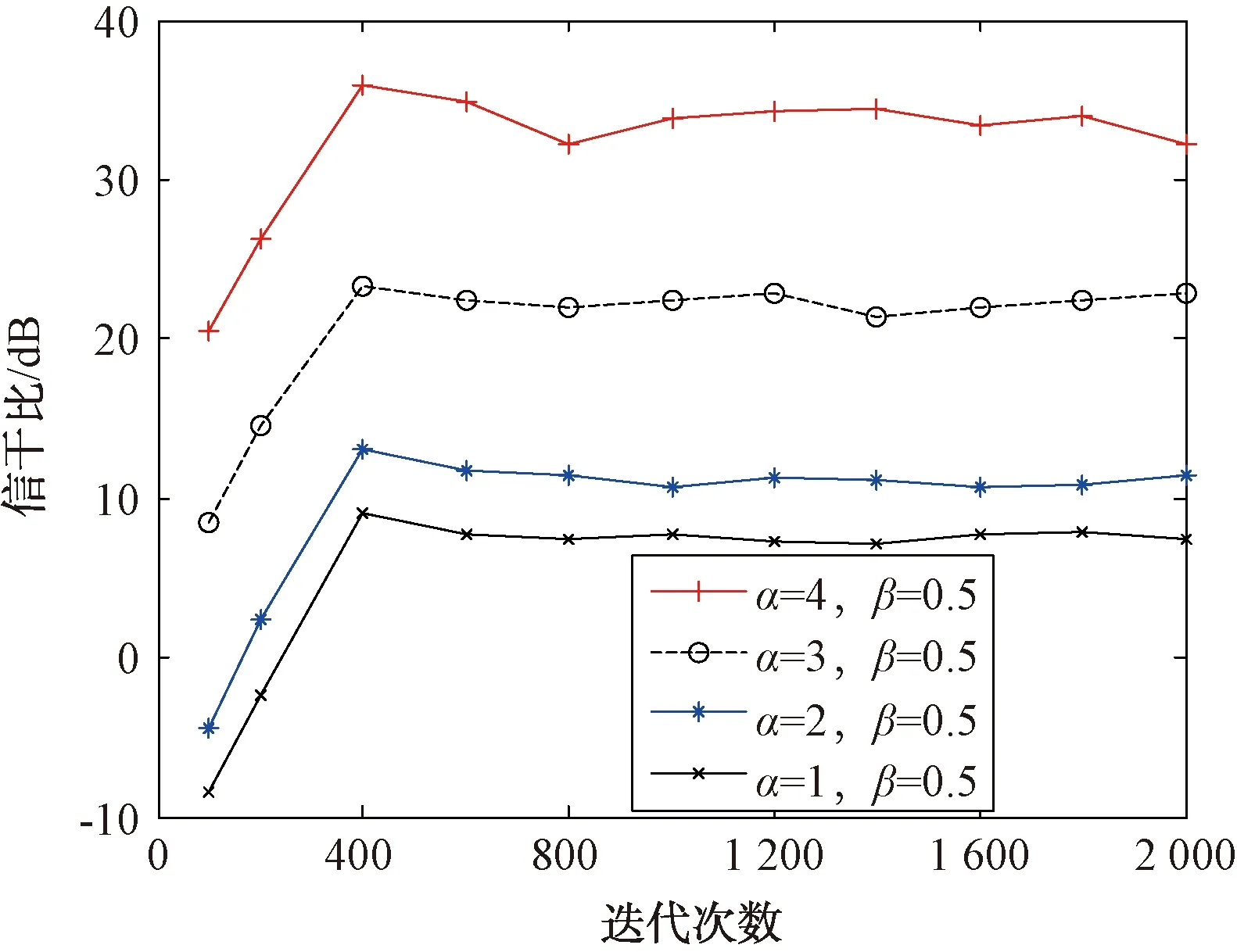
图7 不同α值对情况1的干扰抑制效果仿真图

针对第2种情况下的干扰,通过改变波形控制系数β的值来分析本文所提方法的干扰抑制性能。其参数设置如下:算法处理前,目标回波与灵巧噪声干扰的初始信干比为δSJR=-10 dB,β=0.2,0.3,0.4,0.5,α=1,算法迭代次数N=2 000,其它参数设置情况与3.1节保持一致。经100次Monte Carlo实验,得到算法处理前后的信干比变化随迭代次数的变化情况,如图8所示。由图8可以看出,随着波形控制系数β的增大,其算法处理后干扰抑制效果更加明显。相比于普通抽样函数的波形控制系数β=1时,滤波后的信干比提高了15 dB左右。因此,采用本文所提的改进抽样函数自适应滤波方法,在移频量fyp≠0或|k[τj(m)-τ(m-1)]|的值小于干扰带宽Bj的一半时,可有效抑制灵巧噪声干扰,相比于定步长自适应滤波算法,干扰抑制后信干比至少提高8 dB。通过改变波形控制系数β,可使信干比提高20 dB以上。

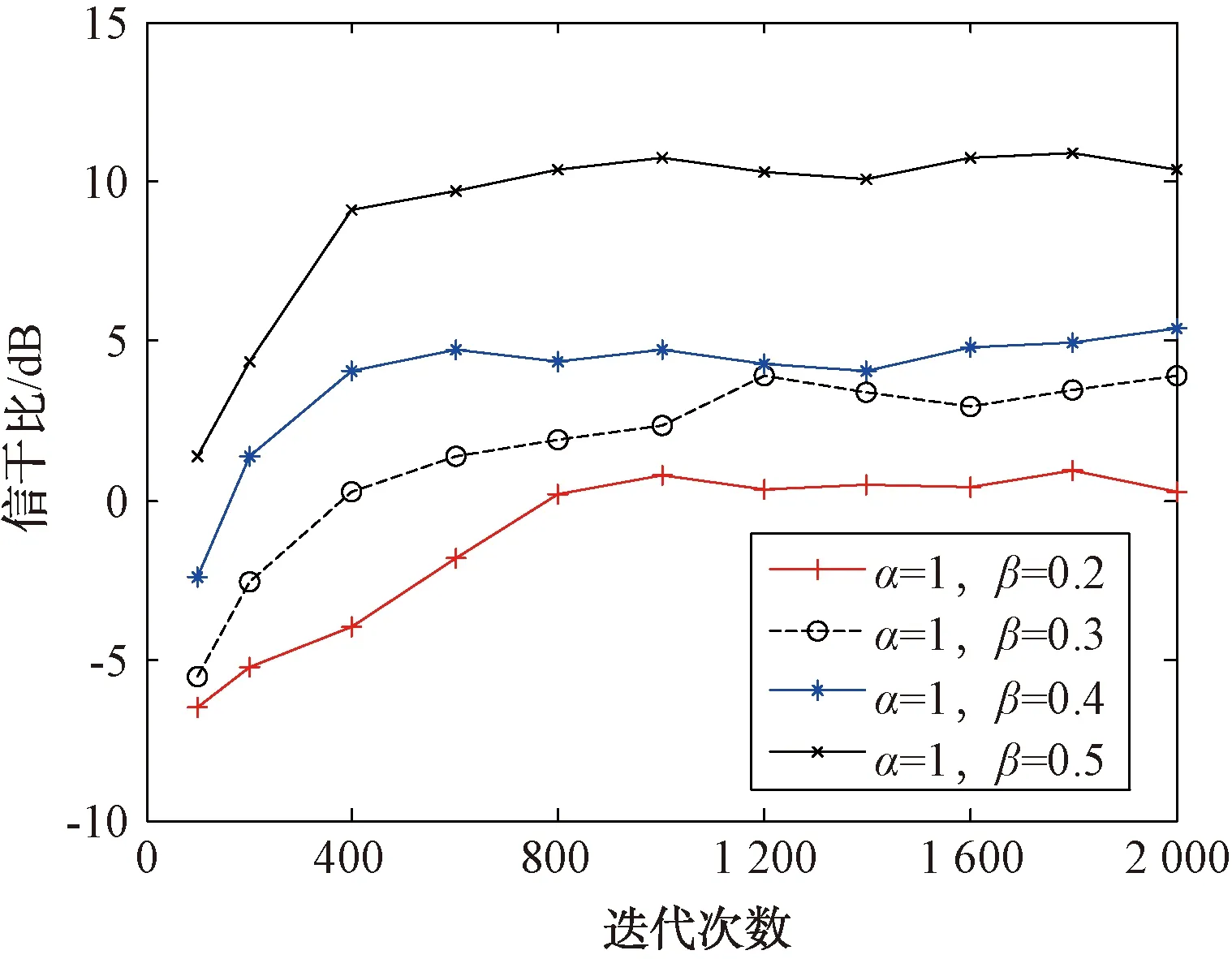
图8 不同β值对情况2的干扰抑制效果仿真图

4 结束语

灵巧噪声干扰对LFM体制的机载雷达产生较强压制性和欺骗性,使目标回波信号在频域上完全被淹没,匹配滤波后干扰对回波造成完全的欺骗效果。针对此问题,本文采用了一种改进抽样函数的自适应滤波方法,通过幅值调整系数和波形控制系数,对差拍处理后的回波信号分量进行滤波处理,并对消灵巧噪声干扰。通过本文的仿真结果可以看出,改进抽样函数滤波算法可有效提取在2种干扰情况下的目标回波,消除灵巧噪声干扰的影响。