舰载近程搜索雷达时空二维海杂波建模与仿真
2023-07-17刘照标张友益
刘照标,张友益,陈 翰
(中国船舶集团有限公司第八研究院,江苏 扬州 225101)
0 引 言
在海战场环境中,舰载近程搜索雷达是发现掠海飞行导弹的重要工具,当雷达以对海模式探测反舰导弹等威胁目标时,雷达不可避免地会受到海面杂波的影响。在雷达论证和仿真评估阶段,研究海杂波的规律并进行合理的建模与仿真是分析雷达对海探测性能的有效途径[1]。同时,在海上大规模体系作战模拟推演过程中,海杂波背景也是不可忽视的因素。
经过多年的研究,人们已经基本掌握了海杂波的分布规律,提出并建立了大量数学模型。在海杂波仿真方面,许多人对单点海杂波序列的仿真做了相关研究,但基于具体场景的时空二维相关海杂波的仿真相对较少。本文以舰载近程搜索雷达为例,对海杂波的仿真流程作了具体的研究,并给出了仿真结果。
1 海杂波特性
1.1 幅度特性
杂波的幅度分布对于杂波环境中雷达性能表征具有重要作用,研究杂波的幅度特性可以设计出稳健的检测器,实际杂波与假设模型相差较大将会导致虚警概率和检测灵敏度出现显著变化。目前,K分布是一种普遍使用的海杂波幅度分布模型,它能够在宽泛条件下匹配海杂波观测数据,并且能够对加性噪声和相关特性进行精确模拟[2]。K分布使用2个因子的乘积来表述杂波的起伏特性,一个是慢变化分量,是杂波的基本幅度控制分量,用平方根伽马函数表示;另一个是快变化分量,指斑点控制分量,用瑞利分布表示。K分布的概率密度函数为:
(1)
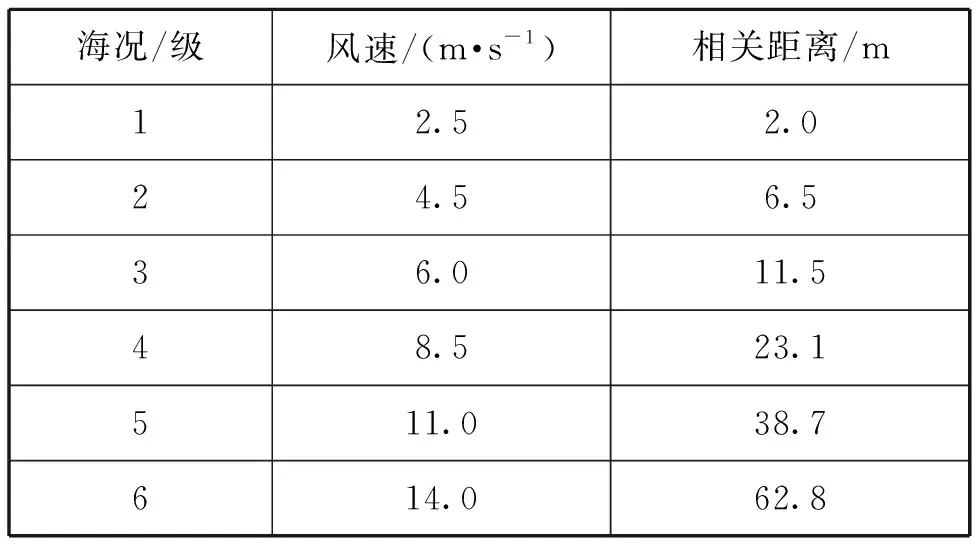
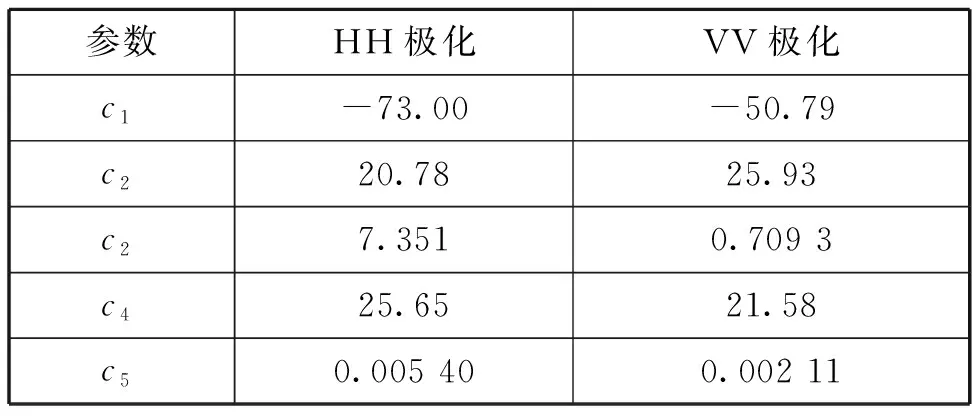
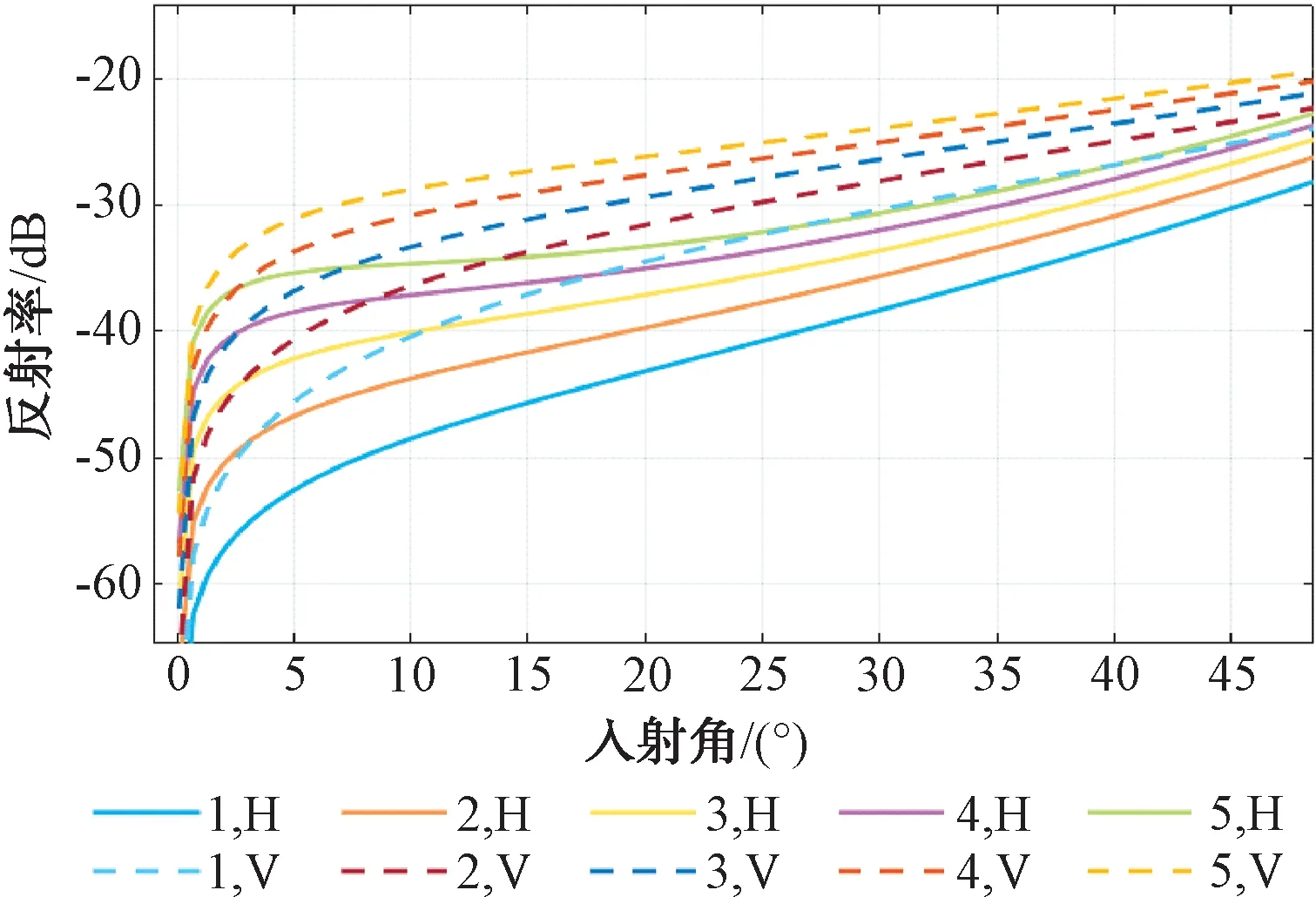
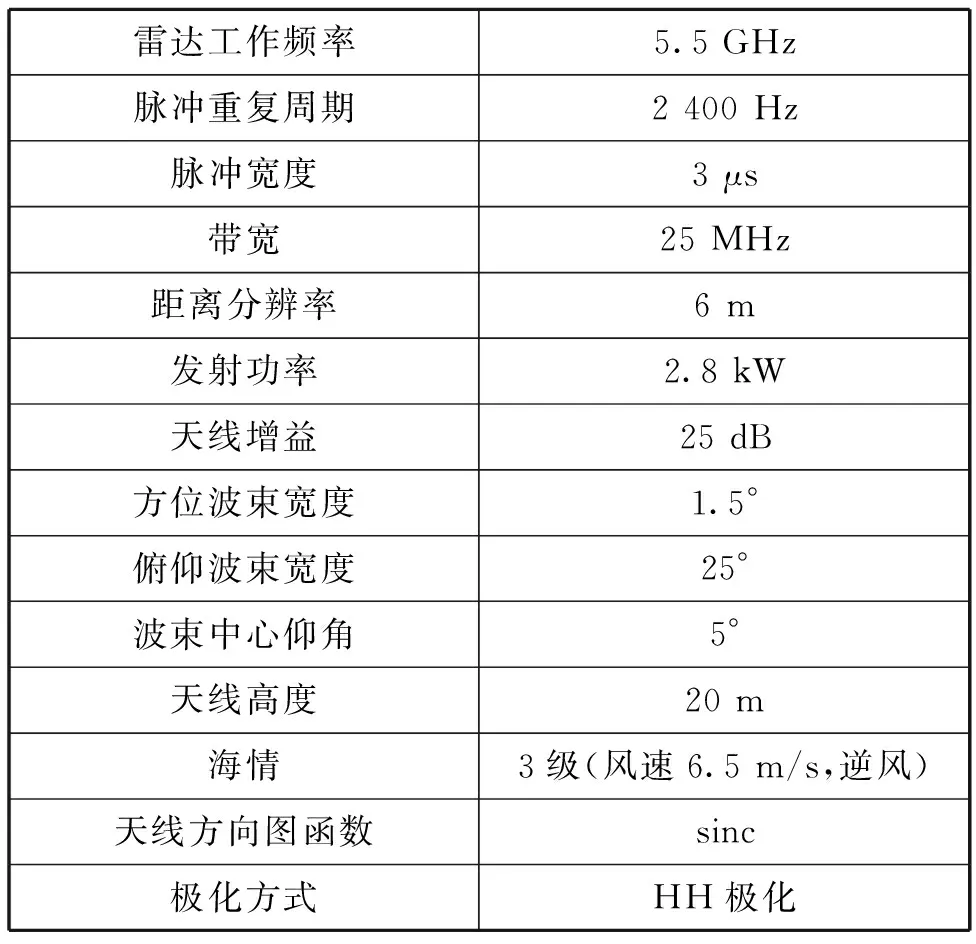
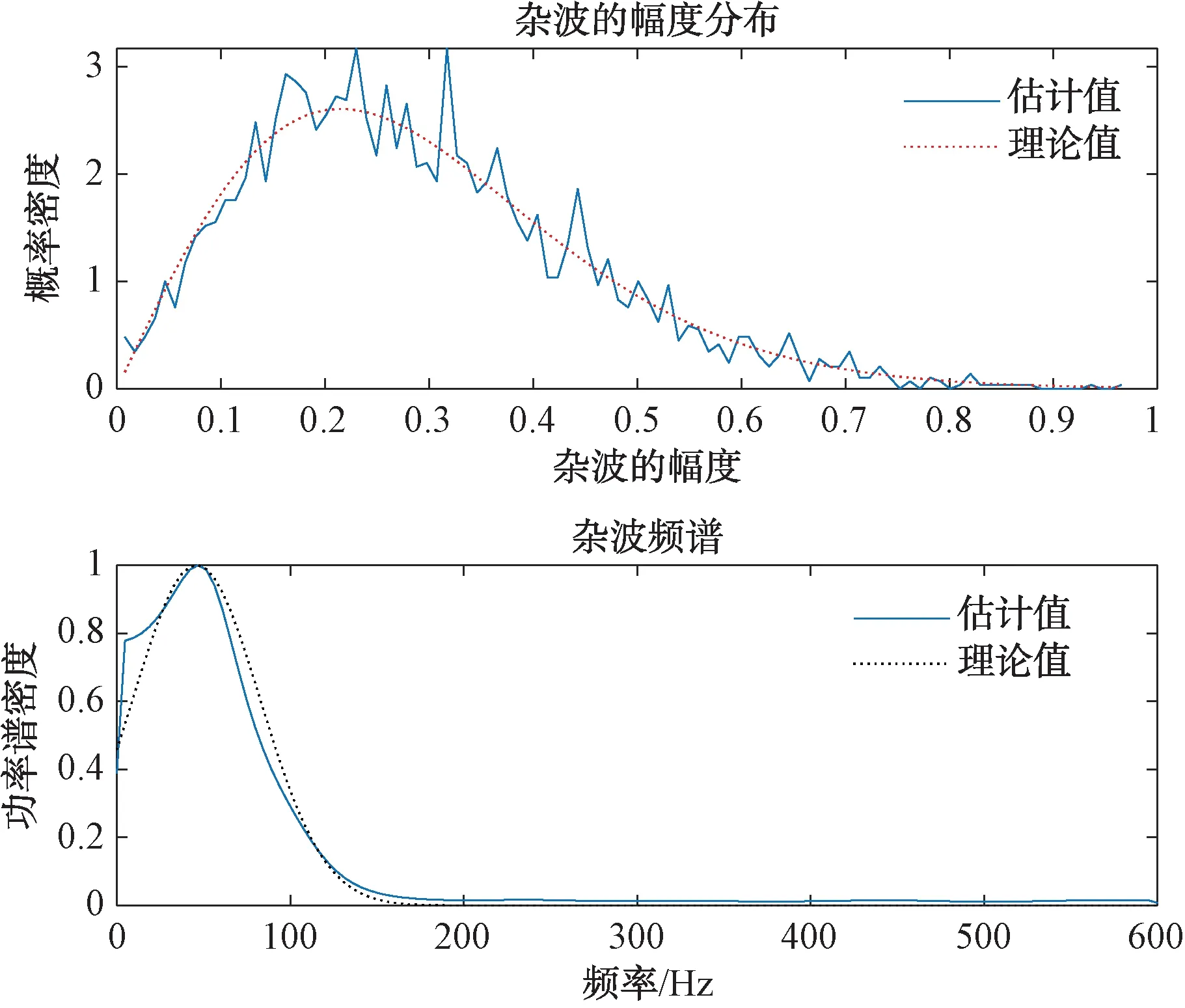
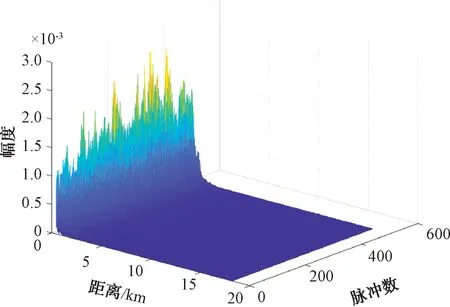
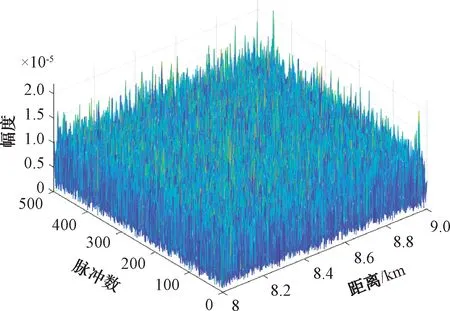
式中:v为形状参数,对大多数雷达杂波来说,0.1 雷达回波的频域处理能够提供海面运动目标与海杂波的附加鉴别。海面的波动和雷达平台的运动导致海杂波具有一定的多普勒频移,且多普勒谱被展宽,其形状与海况等因素有关,研究海杂波的多普勒特性对频域杂波抑制有重要作用。比较常用的海杂波谱模型主要有高斯型、指数型和幂函数型等,在本文中使用高斯型杂波谱,其表达式为: (2) 式中:σf是尺度参数,为杂波谱的标准差,表示了杂波谱的展宽程度;f0是杂波谱的中心频率,即平均多普勒频率,其值与海浪的运动速度有关。 海浪的运动速度反映了海情,在低入射角逆风场景下,多普勒谱平均速度与风速U的关系式为[3]: VVV=0.25+0.18U (3) VHH=0.25+0.25U (4) 杂波谱在变化,但半功率谱宽可以近似表示为: (5) 式中:λ为雷达波长。 海杂波的时空相关性是指雷达接收到的海杂波在时间和空间上的变化存在相关性。时间相关性是指某个距离分辨单元在雷达信号脉冲之间的相关特性,反映了海面的起伏运动情况,空间相关性是指在径向或方位向的不同反射单元的回波之间的相关性。通常将海杂波的时间和空间相关特性进行联合考虑分析研究的时候,可认为海杂波的时间相关性和空间相关性是相互独立的[4]。 海杂波的时间相关函数与功率谱密度函数属于傅里叶变换对,所以对海杂波多普勒特性的研究与时间相关性上的研究在本质上是一样的,多普勒谱分析属于频域分析,相关函数属于时域分析。 空间相关性对雷达目标探测影响较大,直接决定了恒虚警率(CFAR)检测器中的相关检测单元个数的选取[5]。使用最广泛的海杂波空间相关模型是Watts等人[6]提出的一种指数型衰减形式的空间相关函数: (6) (7) 式中:ρ为相关距离长度;U为风速;g为重力加速度;φ为风向与雷达视线的夹角。 在不同海况下的海杂波空间相关距离如表1 所示。 表1 海杂波空间相关距离 海面属于一种表面散射体,通常把雷达照射范围内的海面看作多个散射单元,在雷达参数一定的情况下,海杂波的功率取决于海面反射单元的有效雷达截面积(RCS),RCS大小与后向反射率和反射面积的关系式为: σ0=σ/A (8) 式中:σ0为反射率,是一个无量纲系数,一般以dB形式表示;A为被雷达照射反射单元的面积;σ为被照射的反射单元的雷达有效散射面积(RCS,m2)。 后向散射系数的取值一般与两方面因素有关:一方面是雷达参数,主要包括雷达的入射角、天线极化方式、工作频率等,入射角是最主要的影响因素;另一方面是海面参数,主要包括海况、风速等海情因素。许多科学工作者通过对大量实验数据的观测和总结,提出了许多后向散射系数的经验公式,比较常用的有SIT模型、GIT模型、TSC模型、HYB模型、NRL模型等经验和半经验模型。本文采用文献[7]在2012年提出的NRL模型,该模型的表达式为: c4·(1+S)1/(2+0.085·α+0.033·S)+c5·α2 (9) 式中:α为入射角;S为海况,一般总共有6种海况(即1~6级);f为雷达工作频率。 该模型具有5个自由参数,这5个参数的取值如表2所示。 表2 NRL模型参数 在1~5级海况下,后向反射率与频率的关系如图1所示,雷达工作在5.5 GHz时反射率与入射角、天线极化和海情的关系如图2所示。 图1 后向反射率与频率的关系 图2 后向反射率与入射角、极化、海情的关系 以舰载近程搜索雷达对海探测场景为研究对象,具体仿真参数如表3所示。 表3 舰载近程搜索雷达海杂波仿真参数 首先对舰载雷达照射海面场景进行建模,图3是雷达照射海面的几何模型。杂波反射面积的计算需要考虑雷达对海观察的角度、雷达天线波束形状、雷达距离分辨率,根据几何结构,单个距离分辨单元内的雷达照射面积为: 图3 雷达对海照射几何模型 A=ρRθazsec(φgr) (10) 式中:ρ为雷达距离分辨率;θaz为天线的方位宽度,一般使用3 dB波束宽度;φgr为波束在该分辨单元的入射余角。 由于地球存在曲率,根据几何关系利用地球曲率对入射余角进行修正建模: (11) 式中:h为雷达天线的海拔高度;re为地球半径(乘以4/3以考虑大气的折射影响);R为雷达天线到散射单元的斜距。 Fe3O4-C磁性空心微球中所含的元素可以从材料的XPS谱图得知。如图2(a)所示,材料的XPS全扫描谱图中只有Fe 2p,C 1s,和O 1s的特征峰出现,证明所得颗粒确实是由铁氧化物和C组成[10]。 雷达到地平线(杂波消失的距离)的斜距为: Rh=(h2+2hre)1/2 (12) 在当前仿真参数下,海杂波消失的距离大约为18 km,海面RCS随距离变化的关系如图4 所示。 图4 海面RCS随距离变化情况 杂波序列既有幅度特性,又具有功率谱特性,因此杂波序列的仿真就是模拟同时满足幅度特性和功率谱特性的随机序列。产生这种序列常用的方法主要有2种:零记忆非线性变化法(ZMNL)和球不变随机过程法(SIRP)[8]。ZMNL法的前提是已知非线性变换前后杂波的相关系数之间的非线性关系,而相关K分布难以找到一种适用的非线性关系。SIRP法克服了ZMNL法非线性变换对杂波谱的影响,这种方法允许杂波的自相关函数和边缘概率密度函数分别独立进行控制,该方法的基本原理如图5 所示。 图5 SIRP法原理图 图5中,W1(k)是复高斯序列,线性滤波器H1(z)决定了序列的频谱结构,即杂波的多普勒谱,W2(k)是非负实高斯序列,线性滤波器H2(z)和ZMNL变换使得S(k)的概率密度符合杂波的概率密度函数,且相关时间远大于Y(k)的相关时间,从而不会改变Y(k)的频谱结构,输出序列Y=S·X。 K分布形状参数ν的经验公式为[3]: (13) 式中:φgr为天线波束入射角;A为雷达分辨单元的面积;kpol表示与天线极化方式有关的参数,HH极化取2.09,VV极化取1.39;θsw为关于涌波方向的姿态角,若无浪涌可以省略最后一项。 尺度参数a与形状参数ν、杂波平均功率pc的关系式为: pc=2νa2 (14) 根据雷达回波方程,雷达单个反射单元的杂波有效平均功率为: (15) 式中:μc为脉压系数。 利用式(13)、(14)和(15)即可算出K分布的尺度参数a。 3.3.1 仿真步骤 Step1:根据仿真参数对雷达照射海面区域进行反射单元划分,并计算每个反射单元的面积; Step2:计算雷达波束对每个反射单元的入射角及后向反射率,进一步计算每个反射单元的RCS值; Step3:根据雷达回波方程计算每个反射单元的回波功率,并计算K分布的尺度参数和形状参数,根据仿真参数计算高斯谱参数; Step4:根据Step3的计算参数使用SIRP法生成每个反射单元的相关K分布序列,组成时间相关序列矩阵; Step5:对Step4中的时间相关矩阵使用空间相关矩阵进行空间相关滤波,生成时空二维相关海杂波。 3.3.2 仿真结果 图6为9 km处(形状参数v=8.59)反射单元相关杂波序列归一化仿真结果和多普勒谱仿真结果;图7是该单元处杂波序列的幅度分布和多普勒谱估计;图8第1个脉冲的回波中一段距离杂波的自相关系数归一化仿真,其中距离向采样率为60 MHz;图9为时空二维海杂波的仿真结果,可以看出强海杂波主要分布在近距离单元处;图10为8~9 km距离处的海杂波仿真结果。 图6 9 km处杂波序列归一化仿真 图7 9 km处杂波幅度分布和功率谱估计 图8 第1个脉冲空间自相关系数 图9 时空二维相关海杂波仿真 图10 8~9 km处的海杂波仿真 雷达海杂波对于雷达的检测效果具有重要影响,对海杂波进行精确建模和仿真越来越重要。本文首先分析了海杂波的幅度分布特性、多普勒谱特性、时空相关特性及后向反射特性,并给出了相应的经验模型;然后以舰载近程搜索雷达对海探测场景为对象,研究了时空二维相关海杂波的具体仿真过程,给出了详细的仿真步骤;最后根据实际雷达参数实现了基于K分布的时空二维相关海杂波的仿真。1.2 杂波谱特性
1.3 时空相关特性
2 后向反射率

3 基于K分布的杂波仿真
3.1 海面散射单元划分
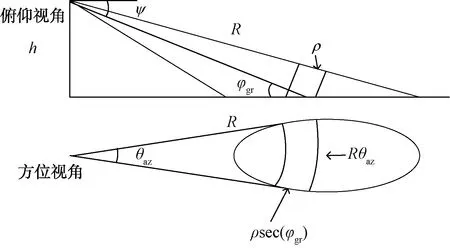
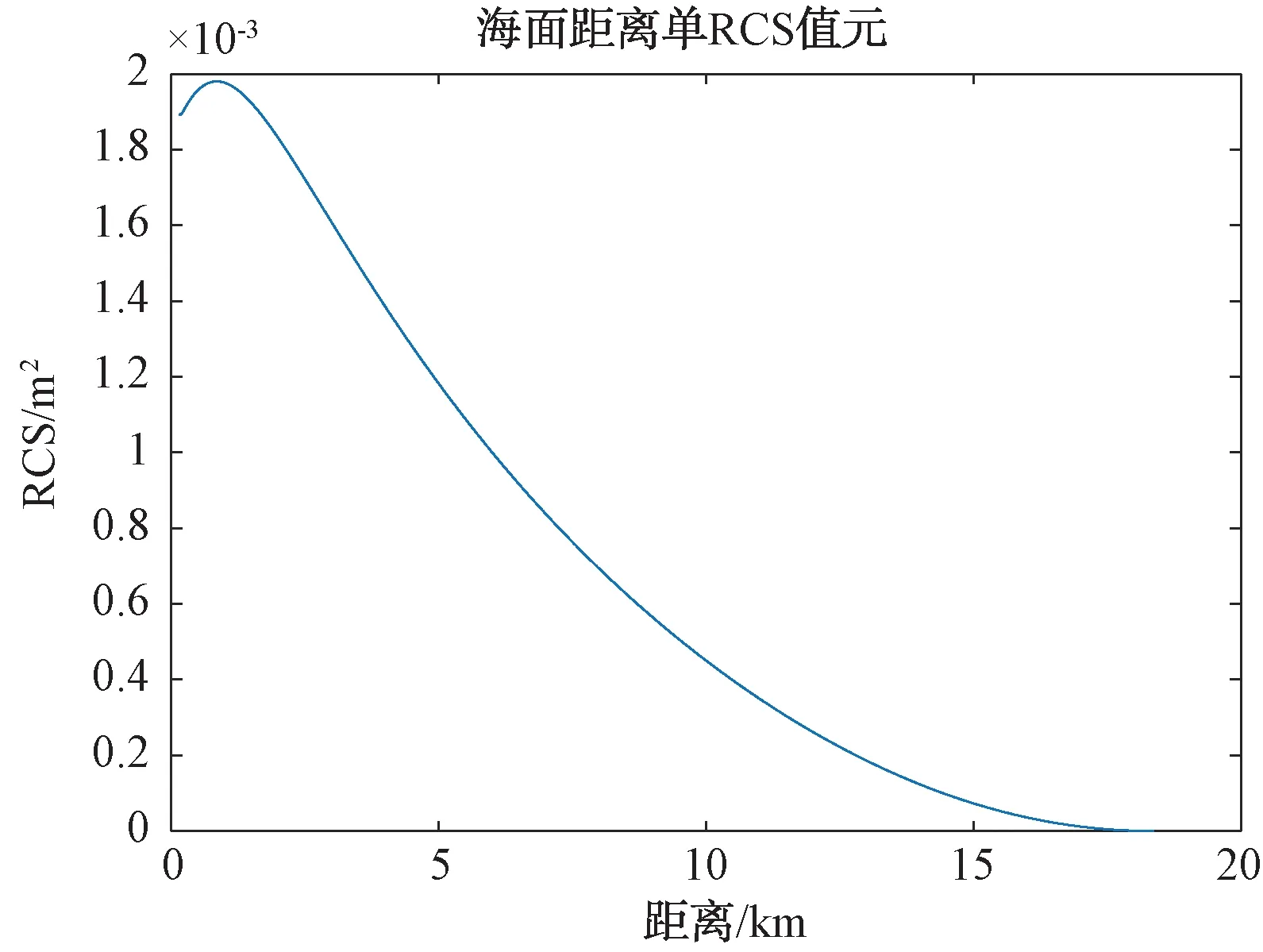
3.2 K分布杂波序列模拟
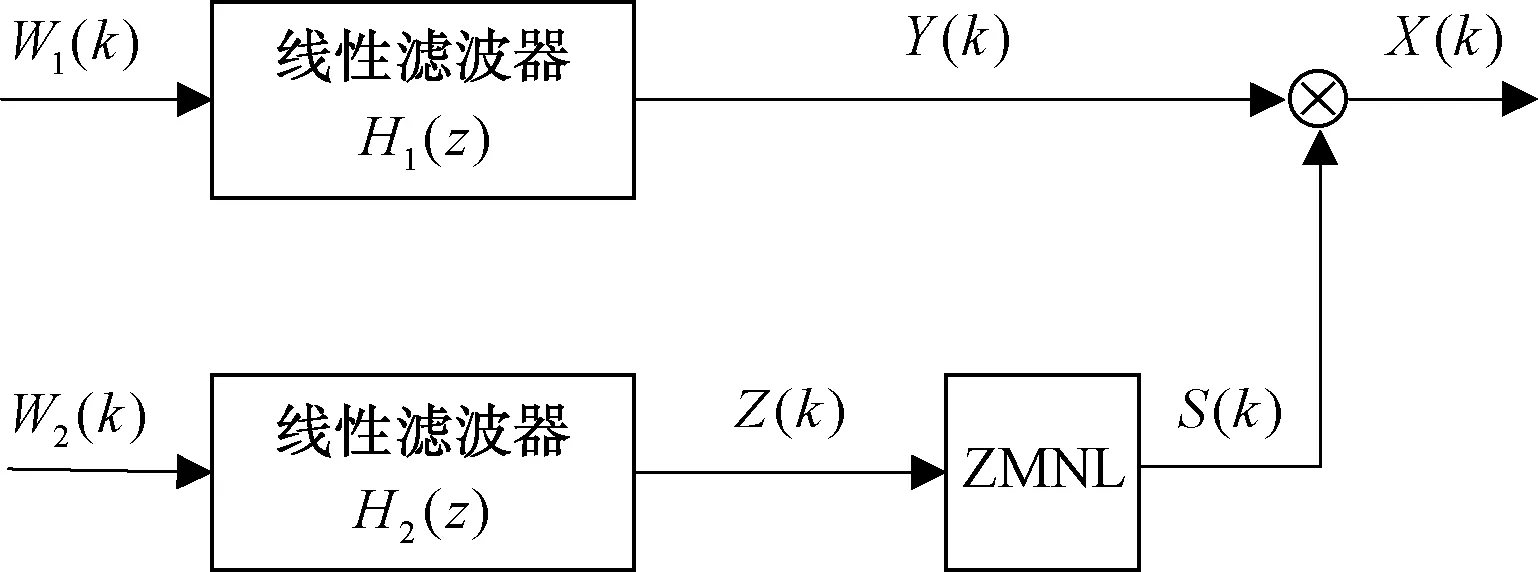
3.3 时空相关海杂波仿真
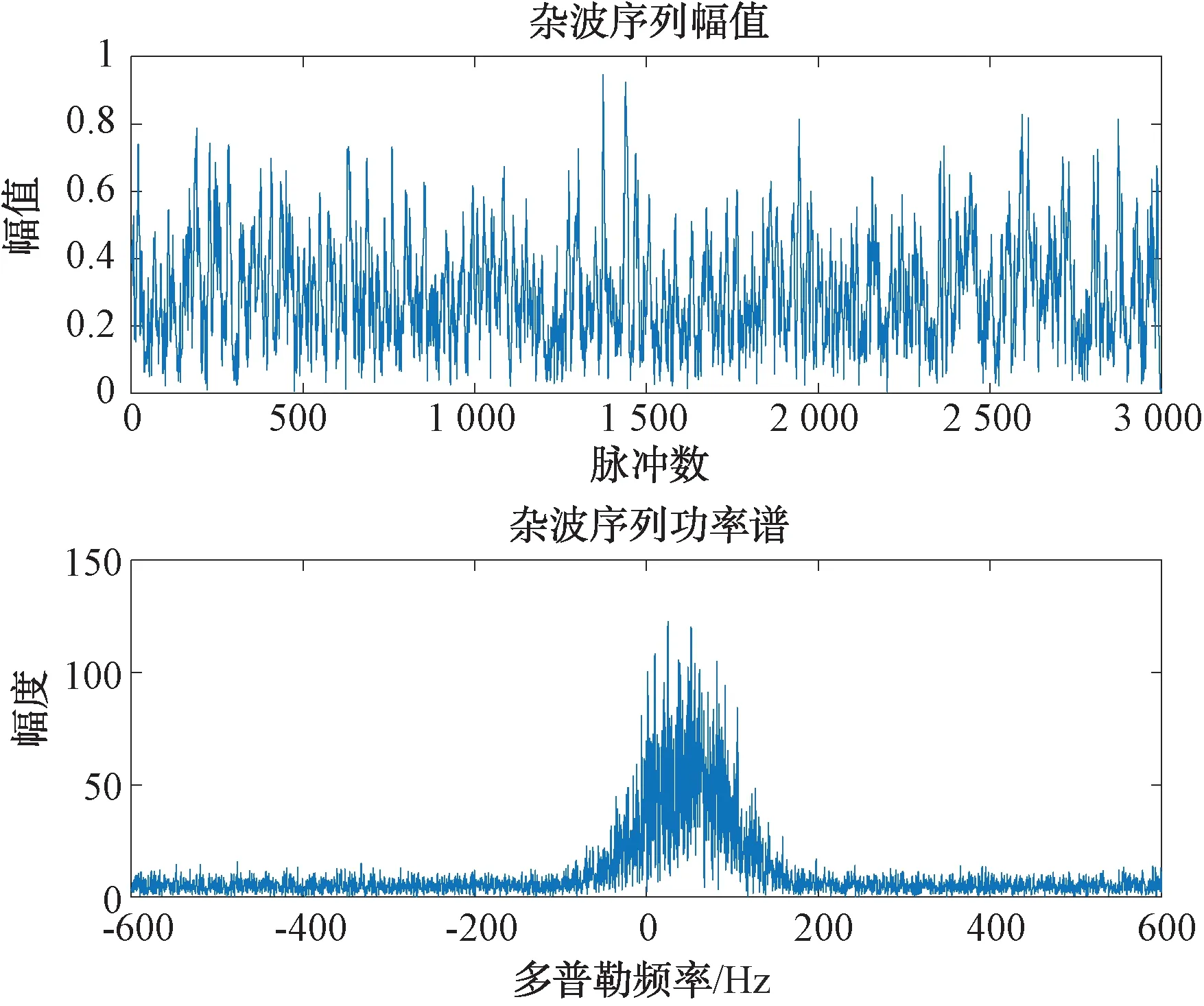

4 结束语
