质疑求证：指向学生理性思维培养的核心区间

【摘 要】质疑求证是在理性思考基础上的批判怀疑和实际求证，是一种基于实证下定论的思维品质，是一种严谨求真的理性精神。教师在教学时制造认知冲突，引发学生质疑求证的内需；暴露相异构想，为学生搭建质疑求证的平台；要求有理有据，培养学生质疑求证的习惯，有助于他们形成理性求真的精神，学会用数学的思维思考现实世界。

【关键词】小学数学；质疑求证；思维品质；理性精神；核心素养

【中图分类号】G623.5  【文献标志码】A  【文章编号】1005-6009（2023）22-0048-03

【作者简介】刘佳，江苏省宜兴市陶城实验小学（江苏宜兴，214200）校长，高级教师，无锡市数学学科带头人。

数学是一门充满理性并教人理性的学科，数学教育的基本价值在于提升学生的理性思维。理性思维是一种基于证据和逻辑论证的思维。质疑求证的理性思维品质、实事求是的科学态度，以及会用数学的思维思考现实世界的能力，是数学课程要培养的学生核心素养。在数学教学中，教师应注意思考如何在传授知识的同时使学生学会理性质疑，善于求证唯真，从而培养会思考、善思辨、有思想的独立的人。

一、制造认知冲突，引发质疑求证的内需

在教学中，对于学生的易错点、易混淆点、认知难点，教师可通过制造认知冲突，引导学生经历质疑求证的过程，反思自己的原有认知，得出结论，厘清知识的核心本质；反思自己的学习过程，形成科学的学习方法和思维方式。这样的学习，是学习真正发生的深度学习；是学生经历知识形成过程，探寻知识背后道理后的深入建构；是“同伴否定—质疑—求证—反思—自我否定—再认知”的理性思维过程，有利于学生学会用数学的思维思考现实世界。

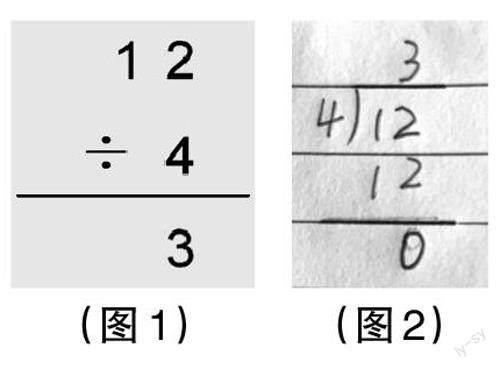
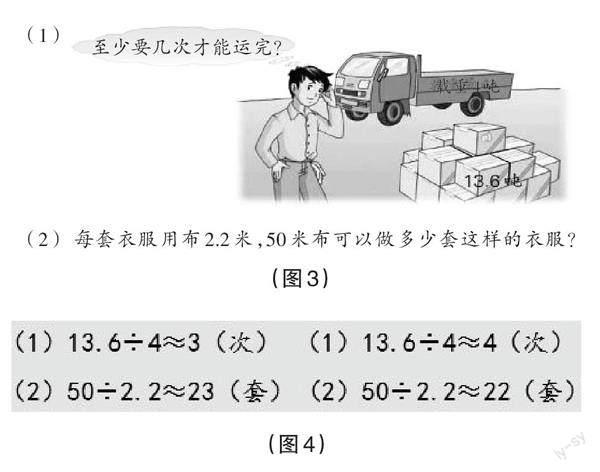
如教学苏教版二下《除法竖式》一课时，教师出示准备题：列竖式计算12+4、12-4、12×4、12÷4。学生独立完成，4名学生上台板演。12÷4，全班48名学生的作答结果，有46人都如图1所示，有2人如图2所示。教师追问哪一种写法正确，大部分学生质疑图2的写法：“我们以前学习的加法、减法和乘法的竖式都不是这种格式，除法竖式写成这样和前面三种运算不一致，肯定不对。”教师没有直接下定论，而是追问2人为什么这样写，他们回答书上就是这样写的。教师进而提问46人：“书上为什么不像你们这样写？书上的写法和你们的写法有什么本质区别？有什么好处？”推动学生自然进入理性求证环节。

上述案例中，加减乘除四种运算，唯独除法竖式的书写格式比较“另类”，教师故意出示数字相同但运算符号不同的准备题，当学生出现不同意见，尤其是得知教材上的写法与自己不同时，产生了强烈的认知冲突，质疑“为什么它的写法不和其他三种运算一致”便成为自然之事。教师以此为切入点，紧追不舍连续进行三个追问，引发了学生理性求证的内需。

二、暴露相异构想，搭建质疑求证的平台

教师在教学中精心搭建质疑求证的平台，引导学生暴露相异构想，使他们经历观察、交流、操作、思考、归纳等过程，最终冲破原有的认识局限，放弃或修正原有的观点。如此，将有助于学生在不断“质疑—操作—分析—思考”的过程中积累分析、解决问题的经验和方法，提升数学素养；在“否定—再否定—最终认同”的过程中明晰质疑求证后的结论更有说服力；在理性质疑、实际求证的过程中，思维逐步由模糊走向清晰、由感性走向理性，有利于学生学会用数学的思维思考现实世界。

如教学苏教版四下《三角形三边关系》一课，在学生得出结论“两边之和小于第三边的三条边不能围成三角形”后，教师追问：“两边之和等于第三边时能否围成三角形？”学生之间出现了不同的声音，教师不作定论，抛出一句：“正确结论的产生从来不是比谁的声音响。”瞬间便激起了学生质疑同伴证明自己观点的好胜心，甲方：“两边之和小于第三边不能围成三角形，原因是短的两条边的‘头靠不到对方，现在4+6=10能‘靠到了，所以能圍成。”乙方：“‘靠到没用，再长一点才能‘撑起来。”教师顺势抛出一句：“口说无凭。”再次将学习推向了高潮。双方各派代表到实物展台上交流，甲方围的被乙方用放大镜清晰地看出两条边之间有缝隙，乙方演示撑起来了以后，不用放大镜便可见中间的缝隙。甲方表示小棒有粗细，所以有一定的误差。乙方：“当‘a+b=c时，三个端点在同一条直线上，这样的三个点能作为三角形的三个顶点吗？”

上述案例中，教师有意识地在教学难点处两次引导学生暴露相异构想，两次为学生搭建质疑求证的平台，在“落入—走出”陷阱的过程中，学生理性思考，碰撞思维，自觉放弃或修正原来的认知，最终形成了正确的认知。

三、要求有理有据，培养质疑求证的习惯

数学语言是数学思维的表现形式，有理有据的表达会让思维更有根据。经常要求学生有理有据地表达，有利于他们在不经意间形成质疑求证的理性思维品质，逐步学会用数学的思维思考现实世界。

1.言之有理

教学苏教版五上《商的近似值》一课，面对如图3所示的问题，学生作业反馈如图4所示。

教师提问：“同一道题会出现两种不同的答案吗？”（学生摇头）教师追问：“既然这样，究竟哪种方法正确呢？”片刻后，全班46名学生，43人选择了第二种。教师引导：“做题不是猜谜语，更不是盲目跟风，要讲道理。”生1：“我们原来是用四舍五入法取近似值的，回过头来思考，13.6÷4虽然等于3.4，但要运完，只能入；50÷2.2虽然结果比22.7多，但还是不够做23套，只能舍。”生2：“取近似值不能简单地四舍五入，有时要联系生活经验，根据实际情况决定舍还是入。”

上述案例中，教师一步步引导学生用道理证明自己的观点。学生在讲道理的过程中不仅理解了知识本质，而且在“质疑同伴观点—听取同伴说理证明—对比反思理性质疑自己的观点—形成正确认知”的过程中，逐步形成了思维的变通性、严谨性、批判性和深刻性等理性思维品质。

2.言之有据

教学苏教版三上《两位数除以一位数的笔算除法》一课，笔算42÷2，学生甲、乙的计算方法分别如图5和图6所示。甲：“乙的写法不正确，应该先算十位。”乙反驳：“以前学的加法、减法、乘法竖式都是从个位算起的，你这样是写反了。”教师引导：“数学是要讲道理的，你有没有办法来证明自己的想法？”甲取出42根小棒（4捆和2根），边演示边说：“把42根小棒平均分成2份，先分整捆的比较快，所以先算40÷2=20。”乙不甘示弱：“先分整捆的或零散的是一样快的。”教师继续问：“如果是52÷2呢？”甲：“5捆平均分成2份，每份2捆，剩下1捆拆开和2根合起来是12根，平均分成2份，每份6根，所以52÷2=26。”乙反驳：“也可以先分2根，每份1根，再分5捆，每份2捆，剩下1捆拆成10根，每份就是5根，合起来也是26根。”教师介入：“甲是先一捆一捆地分，再一根一根地分；乙是先一根一根地分，再一捆一捆地分，然后又一根一根地分，你们觉得哪种分法更方便？”

上述案例中，教师引导学生明白，要让对方心服口服必须用证据支撑自己的观点，要言之有据。当甲的演示不足以说服乙时，教师不急着下结论，而是适时介入，通过提示、提问，引导双方继续质疑求证。在这样一种要言之有据的要求下，学生不仅从内心深处感受到甲这样写的合理性和好处，还在表达的过程中看到了知识背后的道理。更重要的是，这样的过程有利于培养学生证据充分、合乎逻辑的表达能力。经常经历这样求实求真的过程，有利于学生养成理性地思考问题、解决问题的习惯。

综上所述，质疑求证是一种重要的理性思维品质。这个重要品质的培养是一项系统工程，不仅涉及教学方法、教学技巧问题，而且关系到教学原则、教育观念问题。数学教学要着眼学生的终身发展，帮助他们养成理性的思维方式，逐步学会用数学的思维思考现实世界。

【参考文献】

［1］郑毓信.数学思维与小学数学［M］.南京：江苏教育出版社，2012.

［2］马利红，魏锐，刘坚，等.审辨思维：21世纪核心素养5C模型之二［J］.华东师范大学学报（教育科学），2020，38（2）：45-56.

［3］罗鸣亮.做一个讲道理的数学教师［M］.上海：华东师范大学出版社，2016.