Can-Hang不等式的加权推广及引申

山东省邹平双语学校 (256200) 姜坤崇 代民德

文[1]给出了如下的Can-Hang不等式:

本文给出不等式(1)的三种加权推广及引申.

考虑到1≤λ≤4,由(5)、(6)式可得(λ-1)∑x4+(4-λ)∑x2y2-3∑x2yz≥[(λ-1)+(4-λ)-3]∑x2yz=0,即(4)式成立,从而不等式(3)成立,因此不等式(2)得证.

用同样的证明方法可证明以下两个命题(证明均从略):

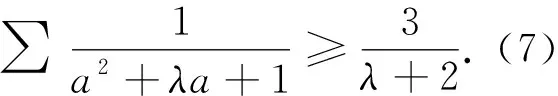
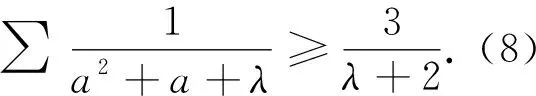
显然,在不等式(2)、(7)、(8)中令λ=1即得不等式(1),因此,不等式(2)、(7)、(8)均为不等式(1)的加权推广.

由命题1中的不等式又可得如下命题4、5中的不等式:

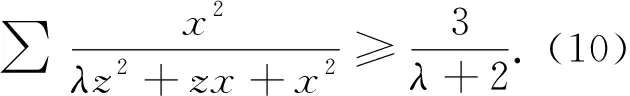
同样的,由命题2中的不等式可得如下命题6、7中的不等式:

命题6 设x,y,z>0,λ≥1,则

命题7 设x,y,z>0,λ≥1,则

由命题3中的不等式可得如下命题8、9中的不等式:

命题8 设x,y,z>0,0<λ≤1,则

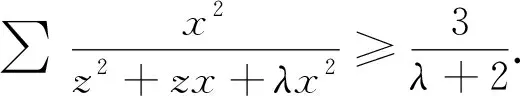
以上4个命题的证明从略.

最后需说明的是,在不等式(9)、(11)、(12)中令x=a,y=b,z=c,λ=1,即得《数学通报》2009年第10期数学问题1818:

因此,不等式(9)、(11)、(12)均为不等式(13)的加权推广.