一道奥赛不等式试题再探究
2023-07-15江苏省姜堰中等专业学校225500
中学数学研究(江西) 2023年7期
江苏省姜堰中等专业学校 (225500) 陈 宇
题目(2021年塞浦路斯奥赛不等式试题)设x,y,z>0且满足x2+y2+z2=3,求证:xyz(x+y+z)+2021≥2024xyz①.
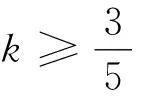
笔者发现,该不等式还可进一步推广,同时存在上界.
推广1 设x,y,z>0且满足x2+y2+z2=3,当k>0,求证:(`k+3)xyz≤xyz(x+y+z)+k≤k+3 ③.

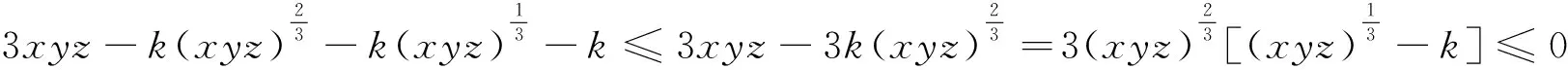
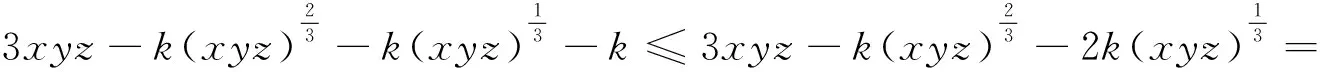
由(1),(2)可知,当k>0时,不等式④成立.进而不等式③,即推广1成立(当且仅当x=y=z=1时,两边同取“=”).
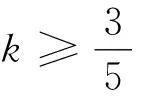
当k=2021时,不等式③即为原赛题,故不等式①,同样存在上界,即
2024xyz≤xyz(x+y+z)+2021≤2024.
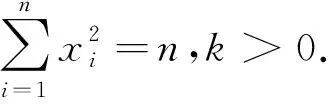
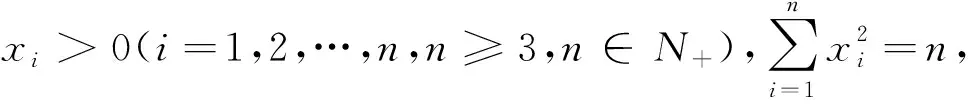
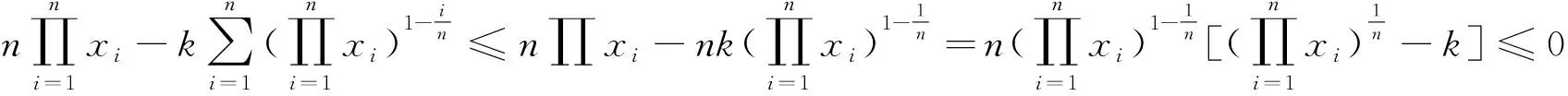

由(3),(4)可知,k>0时,不等式⑥成立.进而不等式⑤左边成立.
即推广2成立.(当且仅当xi=xi+1=1时,两边同取“=”,xn+1=x1.下同).

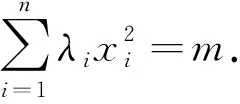
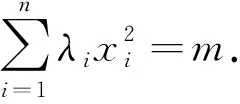
当m=n,λi=1时,不等式⑦即为不等式⑤.

上述推广(推论)由特殊到一般逐层推进,符合认知一般规律.其证明主要运用分析法,适当放缩,分类及排除等数学方法;依据柯西不等式,均值不等式,指数函数单调性,及求解一元二次不等式等知识,从整体入手,进行证明.
