基于改进人工势场法的无人船路径规划
2023-07-13廖卫强乔中飞李光泽
张 丰,廖卫强,2,乔中飞,李光泽
(1.集美大学轮机工程学院,福建 厦门 361021;2.福建省船舶与海洋工程重点实验室,福建 厦门 361021)
0 引言
无人船集船舶设计、人工智能、信息处理和运动控制等专业技术于一体,能够在海洋环境中自主航行并完成各种任务[1]。其中路径规划是无人船技术的重要组成部分,合理的路径规划不仅能使无人船安全避开海上障碍物,还能使其节省时间及能耗。因此,路径规划对于无人船来说有着重要的意义。
目前针对无人船路径规划的算法主要有:粒子群算法、人工势场法、遗传算法、禁忌搜索算法等。其中,人工势场法(artificial potential field,APF)算法具有计算量小、原理简单和生成路径平滑等优点,因此,被广泛应用于无人船的路径规划[2-4]。但经典人工势场法尚存在一些不足[5-8],如:目标点不可达、局部极小值、路径振荡及冗余等。因此需要对该方法进行改进。
对于传统人工势场法存在的问题,目前已有多种改进方法。刘翰培等[9]在危险区域融合模糊控制算法,克服了传统人工势场法的局部极小值问题;Zhou等[10]将人工势场法结合粒子群算法优化切向向量,改善了目标点不可达问题;林洁等[11]通过引用模拟退火算法,改进传统人工势场函数,提出“沿边走”的策略,有效解决了容易陷入局部极小值问题;任工昌等[12]在传统势力场基础上引入障碍物速度斥力场函数,实现机器人的动态路径规划;胡杰等[13]提出一种用偏转角度来构建附加牵引力的方法,以解决局部极小值问题;Guang等[14]提出利用分段混合算法改进势场函数,解决目标点不可达及局部极小值问题。
本文针对无人船人工势场法路径规划中的问题,对斥力函数进行改进,以解决目标不可达问题。通过艏向角限制,使船舶无法进行大角度折返运动,限制船舶下一点位移,使其离开单一障碍物引起的局部极小值问题;通过增加随机扰动量,从而使引力出现误差,解决多个障碍物造成的局部极小值问题;通过路径优化,减小路径振荡,实现路径的平滑性。
1 传统人工势场法基本原理
人工势场法由引力势场和斥力势场组成[15]。目标点对机器人产生引力作用,障碍物对无人船产生斥力作用,在引力与斥力合力作用下无人船向目标点移动。
传统的斥力势场函数为:
(1)

(2)
式中:Fr为障碍物对无人船的斥力。
结合式(1)和式(2)可以发现,当dji≤d0时,随着无人船和障碍物之间的距离dji的减小,斥力势能Er和斥力Fr都会上升;当dji趋近于0时,斥力Fr会接近无穷大。
2 改进人工势场法
2.1 斥力函数修改
从式(1)可以知,当目标点和障碍物之间的距离很近时,障碍物斥力会大于目标点引力,导致无人船无法到达目标点。在传统的斥力势场函数上,添加无人船与目标之间的距离,修改斥力函数,从而解决目标点不可达问题。改进斥力势场函数为:
(3)
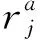
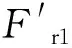
2.2 施加艏向角限制增加随机扰动
局部极小值问题是指船舶在移动过程中的某个时刻,在当前位置下目标船舶受到的引力与斥力大小相等,方向相反,导致当前位置点船舶合力为0,船舶不再移动或者在小范围内往复抖动的现象。典型的局部极小值问题可以细分为两种情况。1)在船舶与目标点之间存在单一障碍物,且船舶、障碍物和目标点处于同一直线。此时,随着船舶逐步向目标点运动,斥力逐渐增大,引力逐渐减小,当运动到某个斥力与引力大小相近的位置,船舶在该处停止或者在该点处往复抖动,导致船舶无法到达目标点,如图1a所示)。2)在复杂障碍物情况下,多个障碍物组成的复杂障碍物环境所产生的总斥力与目标点产生的引力合力为0,导致船舶无法到达目标点,如图1b)所示。
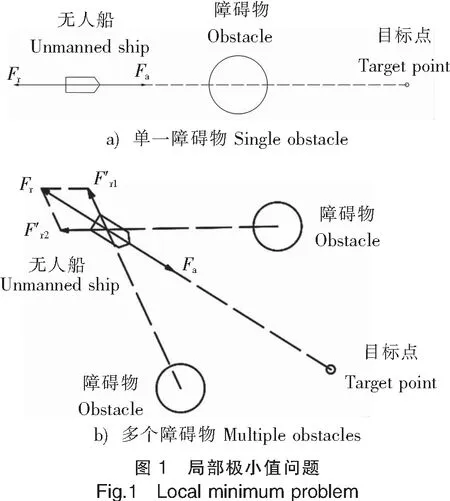
对情况1与情况2分别进行处理。 局部极小值状态判别为ρ(Xj,Xj-b) 针对情况1),通过加入艏向角限制,使船舶无法进行大角度折返运动,其最大艏向角为60°。该限制能够对船舶在后续位置的位移施加控制,使其离开局部受力平衡状态。 针对情况2),施加随机扰动。当出现多个障碍物的局部极小值时,无人船下一步计算出的引力随机地出现误差,引力偏离正常值,使无人船跳出局部极小值。若仍陷于局部极小值,则继续产生新的随机误差,直至无人船走出局部极小值。Fa=dEa/drj=karj·kb。式中:kb为随机扰动量,取值50%~200%。为了避免在随机扰动之下船舶会撞上障碍物,扰动量的大小必须适当,太大船舶可能撞上障碍物,太小可能不足以跳出局部极小值。此外,施加随机扰动后,虽然无人船会跳出局部极小值,但是由于随机性,无人船很有可能会在原地来回走动多次才会成功跳出,在这个过程中,会产生冗余的路径。 按照斥力修改方案,修改传统人工势场法的斥力函数,然后进行仿真模拟。引力系数ka=15;斥力系数kr=5;障碍物的斥力影响距离d0=2.5;rj的指数a取值为2。 运行修改斥力函数后的人工势场法,结果如图3所示。图3a)显示传统人工势场法无法到达目标点;图3b)为修改斥力函数后人工势场法的仿真结果,成功抵达目标点。证明修改斥力函数之后,解决了无法到达目标点的问题。 在修改斥力函数的基础上,施加随机扰动,使无人船具有跳出局部极小值的能力,随机扰动设置为使引力在正常值的50%~200%之间变化。 创造含有以下两种的局部极小值环境。 1)在没有施加艏向角限制的情况下进行仿真,运行结果如图4a)所示,无人船在坐标点(4,5)周围陷入局部极小值。随后在施加艏向角限制的情况下进行仿真,运行结果如图4b)所示,已经具备了解决局部极小值的的能力。 2)在没有施加随机扰动的情况下进行仿真,运行结果如图5 a)所示,无人船在坐标点(5,6)周围陷入局部极小值。随后在施加随机扰动的情况下进行仿真,运行结果如图5 b)所示,已经具备了解决局部极小值的能力,但是会形成冗余及部分振荡路径。 针对无人船在海面上因为增加随机扰动而产生路径振荡的问题,进行减小路径振荡的仿真,着重选择出现路径振荡的环境进行仿真。仿真结果如图6所示,比较图6a)、图6b)可以看出,减小路径振荡之后,路径的平滑性提高了。 本文在传统的人工势场法基础之上,通过修改斥力函数,加入了无人船和目标之间的距离这个因素,克服了船舶无法到达目标点的问题,提高了人工势场法的可行性,但需要注意目标点上存在障碍物的情况。采用施加船向角和增加随机扰动的方法来应对局部极小值问题,仿真结果显示,路径在陷入局部极小值之后,会经过一段路程后跳出,但是由于其随机性,在路径跳出局部极小值的过程中会留下一段无效的路径。为了改善路径振荡和施加随机扰动时产生的无效路径,提出一种路径简化的措施,通过去除一些振荡的路径点,让路径变得平滑。 改进后的人工势场法具有静态和动态障碍物的仿真环境中进行路径规划,探索将人工势场法应用在无人船路径规划的可行性,为无人船技术的研究提供了更多的思路。2.3 路径简化
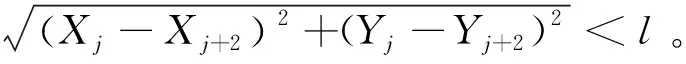
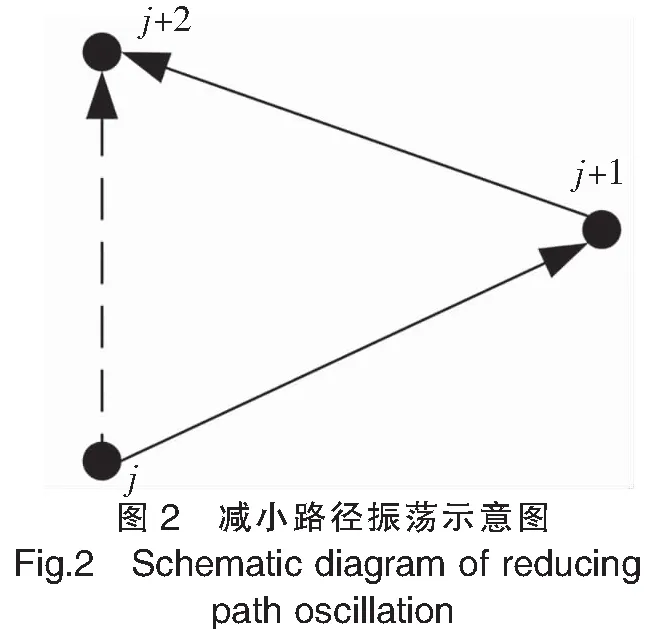
3 仿真结果与分析
3.1 目标不可达现象仿真分析

3.2 局部极小值现象仿真分析
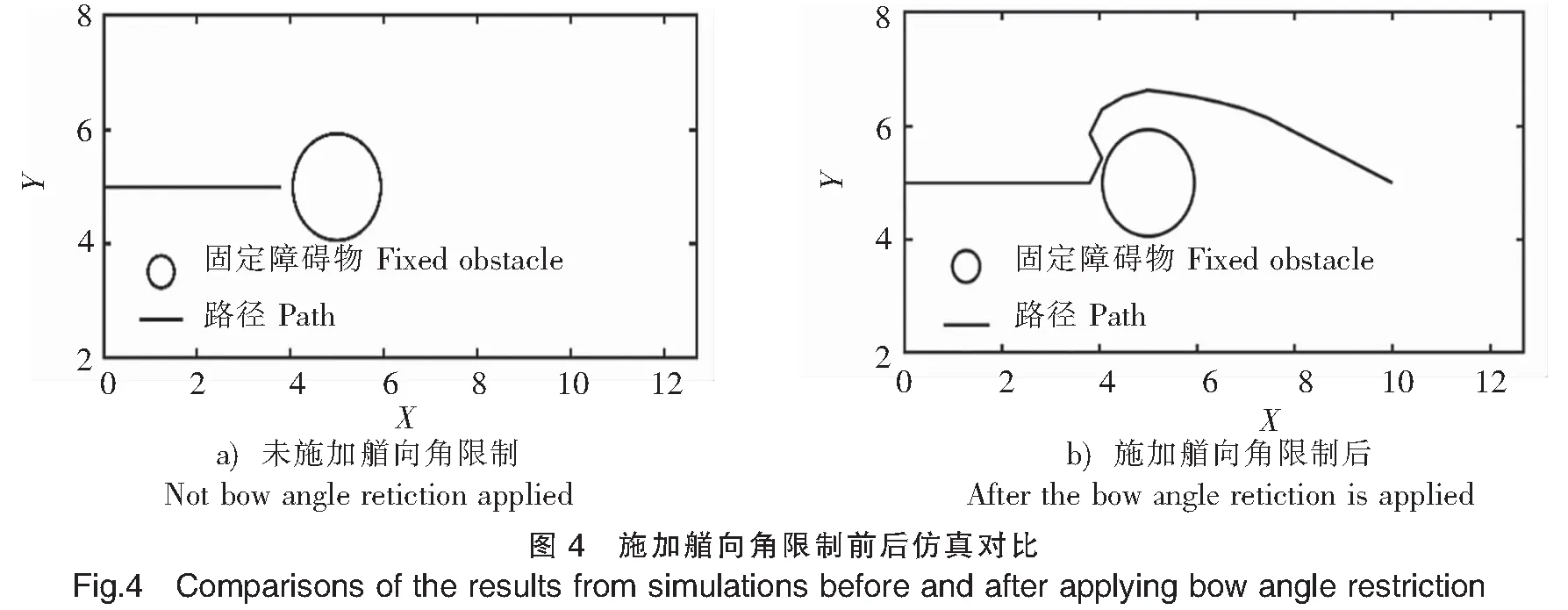
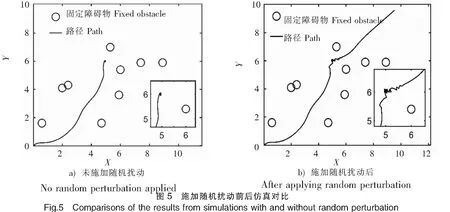
3.3 路径振荡现象仿真分析

4 结语
