考虑法兰变形的U-E金属密封结构匹配优化设计

王晨威,闫方琦,李智军,常 涛,陈建华

(西安航天动力研究所,陕西 西安 710100)

0 引言

金属密封作为低温液体火箭发动机的重要零部件,广泛用于低温管路、高温管路、涡轮泵、阀门系统中,起到隔离介质、保护系统的作用,在发动机高/低温、高压、摇摆、振动等复杂工况环境以及法兰结构变形和装配变形的影响下,极易出现介质泄漏,引起密封失效。金属密封分为单道密封和双道密封,单道密封包括O形密封、C形密封等;双道密封在单道的基础上又增加一道密封,在第一道密封发生泄漏时,第二道密封可以及时阻止介质泄漏[1-7]。U-E密封作为自紧式双道密封的典型结构,在工作时,密封悬臂受到高压介质的挤压产生弹性变形并张开,密封比压增大从而产生自紧作用,冗余式的复杂结构设计有效提升了密封环的回弹性和可靠性[8-9],但给密封的设计带来较大困难。国内关于U-E金属密封的研究较少。马莹等利用有限元模型对U-E密封进行了建模分析,并对主副密封唇压缩量变化进行了研究[10]。而在其他异形金属密封的研究上,杜宸宇等将法兰看成刚体对多种异形结构金属密封环进行了力学特性数值研究,得出不同密封环适用的不同环境[11]。上述研究都未考虑实际工作情况下的法兰变形与倾斜问题,实际工作中法兰的变形会导致U-E主/副面之间的压缩量存在差异,进而导致主/副密封面压强不匹配,但可以从密封结构方面改善这一情况,通过设计U-E主/副密封悬臂的高度差来匹配法兰的倾斜变形量大小。关于法兰、螺栓和密封结构的研究很多。薛杰等将法兰视为刚体,对工作压力下法兰结构的螺栓和密封件受力进行了分析[12]。Nash等分析了螺栓预紧力对法兰的影响,发现加压后法兰出现明显的变形[13]。Lin等对反应堆压力容器进行三维瞬态密封传热分析,比例RPV法兰仿真结果显示上法兰和下法兰分别出现了不同程度的轴向偏斜[14]。Yu等通过采用弹塑性非线性接触来分析HTR-10压力容器的法兰应力和变形,结果表明法兰表面塑性变形较大,增加法兰高度和封头厚度有利于密封性能[15]。上述文献均揭示了系统加压后法兰存在变形倾斜问题,但其法兰螺栓密封结构系统采用的密封件为单道式垫片密封,并无对特型密封件的研究。因此,对U-E密封系统的法兰变形问题,需参考上述文献中常用的法兰变形理论。在文献[16]规范中对法兰变形的计算方法有Walters法和PVRC法。Walters法基于弹性梁[17]和圆平板弯曲理论,并且将螺栓法兰的联接视为静定结构,省去了预紧和工作时螺栓载荷的变化,是一种简化的应力计算方法。PVRC方法[18]是在Walters法的基础上,加入了带泄漏率准则的螺栓—垫片载荷新计算方法。由于PVRC方法将垫片作为一个重要研究对象,不适用于异形截面密封环,因此在特型截面U-E密封的研究中,着重采用Walters法进行分析。

对于U-E密封复杂结构问题,在主/副密封匹配设计之后,可对主/副密封结构进行分体设计,由于设计参数众多,全面设计试验耗费时间较长,可采用研究多因素多水平的一种常用设计方法——正交试验,基于虚拟正交试验可实现方案快速迭代设计,获得多因素影响下的最优解。

因此,本文基于Walters法兰变形分析法计算出法兰变形量大小及法兰主/副密封面分离量差异,找出主/副密封比压差异,通过主/副密封面分离量和密封比压差异对主/副密封进行匹配设计,并利用虚拟正交试验对多结构参数下的复杂密封结构进行分体设计。

1 法兰变形模型及有限元建模

1.1 密封工作过程描述

U-E金属密封的泄漏分为3种,即初始泄漏、工作泄漏、卸载泄漏,分别对应于3个工作过程,是否发生泄漏问题通常用密封比压进行表示,当密封比压大于介质压强的10倍以上,则认为该密封不发生泄漏。

初始泄漏是指U-E密封存在设计缺陷或加工缺陷,在法兰未充入高压介质,就发生密封比压不足,导致密封失效。工作泄漏是指法兰在高压介质的作用下发生分离、偏斜,使密封比压不足,导致密封失效。卸载泄漏是指高压介质泄压,U-E密封悬臂回弹与法兰回弹跟随性不匹配,出现密封比压为0的瞬间,发生泄漏。3种泄漏问题中,故障率最高的是工作泄漏。在工作时,法兰的受力如图1所示,其中A、C为法兰接触的主密封面,B、D为法兰接触的副密封面,主密封泄漏后,高压介质充入副密封悬臂。这些力导致法兰产生分离和偏斜,引起密封比压的变化。通过仿真模型分析法兰偏斜量大小,对U-E金属密封的主/副密封比压设计有一定的参考意义。

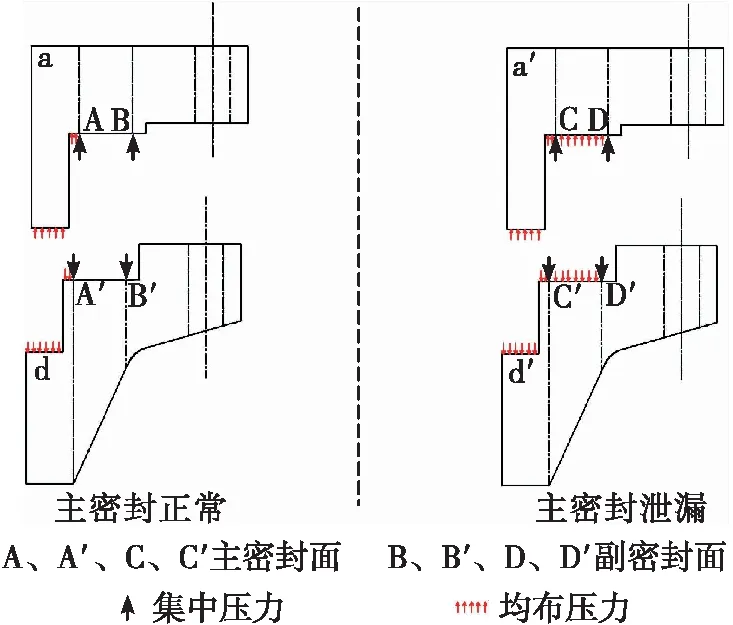
图1 法兰受力简图Fig.1 Flange force

1.2 数学模型

密封比压是评判金属静密封性能的一个重要指标,密封比压即密封面接触压强,密封比压的大小受材料、法兰变形、密封结构等多种因素影响,U-E金属(见图2)密封的密封比压可以表示为

图2 U-E密封结构Fig.2 U-E seal structure

p=f(M,δ,GM,GS,GMS)

(1)

式中:p为密封比压;M为材料参数;δ为法兰变形,包括法兰轴向分离、法兰倾斜变形等;GM为主密封结构,包括悬臂长度、悬臂张角等;GS为副密封结构,包括悬臂厚度、悬臂张角等;GMS为主/副密封相关匹配结构,主要为主/副密封悬臂高度差。

由于密封比压表述式为隐式表达式,因此需要对其中的参数进行独立分析。GH145材料具有良好的硬度和回弹性,因此本文U-E密封材料选取为GH145,即M不作为研究对象,对其他4个参数进行分析设计,通过法兰倾斜变形量大小,找到主/副密封面回弹差异,从回弹量的差异大小对主/副密封的高度进行差异化设计;主/副密封高度匹配完后对主/副密封进行分体正交优化设计;研究思路见图3(p0为介质压强,当密封比压p>10p0认为密封性能良好)。

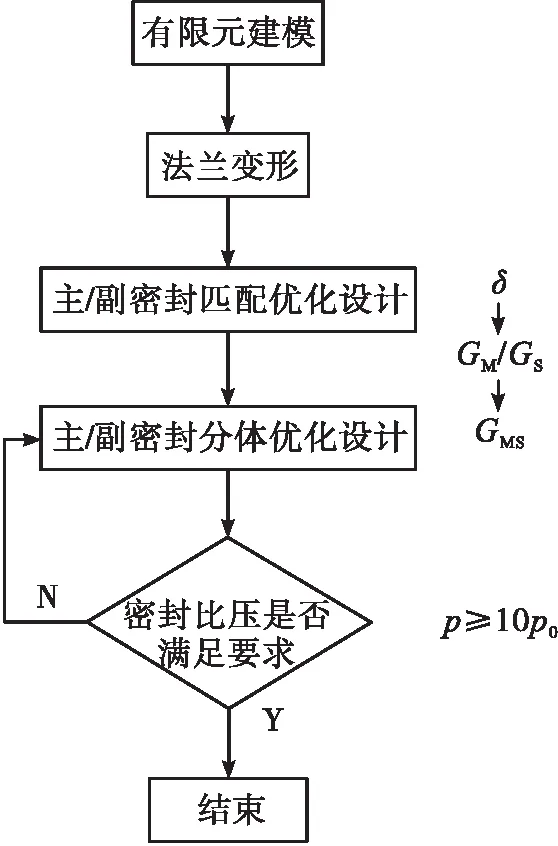
图3 研究思路Fig.3 Research flow chart

1.3 基于Walters法的法兰变形分析

在分析法兰的分离和变形时,对法兰、螺栓、密封环共同进行分析,结合Walter利用结构力学的方法进行受力分析与边界条件的设置。将法兰沿着周向按单位长度进行均分,取分出的一部分进行分析,该部分厚度较小可近似看做拉伸体,基于Walters法,此时,将法兰和螺栓视为悬臂梁结构。螺栓连接处视为固定端,法兰受介质压强部分视为受到均匀载荷,法兰受密封环反力部分视为受到集中载荷,均为纯弯矩载荷(见图1)。值得注意的是,法兰内腔受到的介质压强所产生的周向载荷在周向分布均匀,即被法兰本身所抵消,为平衡力;在法兰管道内受到的介质压强所产生的轴向力没有作用在法兰截面上,并且只引起螺栓在轴向的长度拉伸,分析时可将这两个力忽略。

法兰的变形采用挠度表示,利用能量守恒原理计算法兰在主密封面和副密封面处的挠度差值,即线弹性体由于变形储存的应变能U等于外力所做的外力功W。根据Clapeyron原理有[19]

(2)

式中:Fi为外载荷;δi为所有载荷共同作用下的最终位置。

法兰为均匀材料,利用材料的应力(σ)—应变(ε)关系曲线,计算出应力单元体的应变能密度为

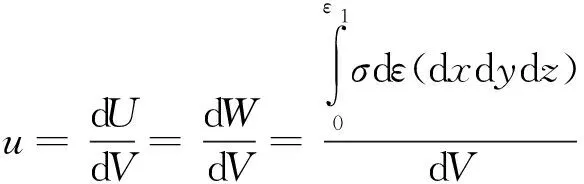
(3)

卡氏第二定理中指出,线弹性结构的应变能U对作用在结构上的某个载荷Fi的偏导数等于该载荷作用点沿该载荷作用方向的位移δi。法兰受力简单,简化模型后不受扭矩和轴力,即

(4)

式中M(x)为法兰所受弯矩,包括集中力和均布力。

将法兰假设成为悬臂梁结构时,法兰材料在变形的线弹性范围内,根据挠度计算定理,法兰的挠度和转角与所受到的力为线性关系,并且法兰的弯曲变形很小,所以当法兰上同时作用了多个力时,任何一个力所引起的变形不会受到其他力的影响,可以对各个力所引起的挠度进行代数相加。

1.4 法兰—密封—螺栓仿真建模

图4为螺栓—密封环—法兰结构模型,其材料参数见表1和图5,整体结构及所有弯矩为轴对称形式,因此按照模型周向的24个螺栓将结构分成15°块模型进行分析。螺栓和垫片统一采用球面螺栓和球面垫片,采用此规格的螺栓和垫片保证了在螺栓或法兰发生偏斜时,垫片施加的压紧力始终垂直于法兰接触面[20],并根据Walters法对仿真模型的边界进行设定,即将下法兰螺栓伸出底端固定;上法兰与密封环边界条件设置在柱坐标系下,约束其前后端面沿周向的转动和径向的位移。根据Clapeyron法对仿真模型中求解方式进行选定。

表1 材料的力学性能参数Tab.1 Mechanical properties of materials

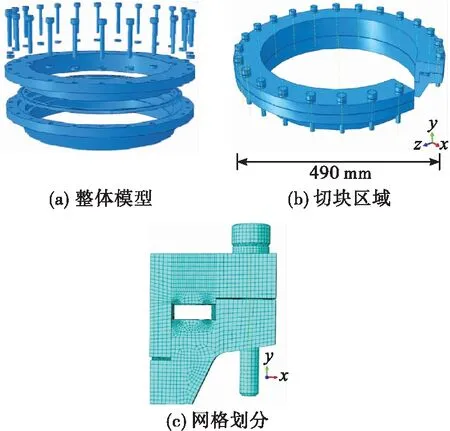
图4 螺栓—密封环—法兰切块模型Fig.4 Model of bolt-seal ring-flange structure

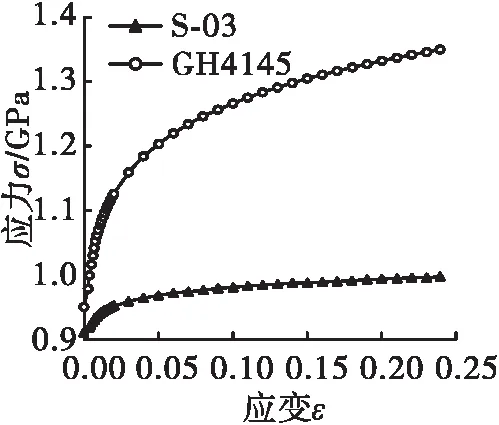
图5 GH 4145 和S-03钢材料应力—应变图Fig.5 Stress-strain curve of material GH4145 and S-03 steel

模型中法兰和U-E密封为六面体网格(C3D8R),螺栓头部下端网格为四面体网格(C3D4)。U-E密封环主副密封唇处和上下法兰主副密封接触面处采用较主体网格(1 mm)更细化的尺寸为0.1 mm的网格,以保证接触位置和密封比压的计算精度;法兰和螺栓不承受大应力部位采用大尺寸网格。螺栓与垫片、垫片与法兰之间的接触采用无摩擦的光滑接触,螺栓与法兰、主副密封唇与法兰的接触采用粗糙接触,摩擦因数为0.149[21]。为避免跳跃式的突变,螺栓位移设置幅值曲线平滑系数为0.2。

整个仿真过程共设置为3个阶段[仿真时长设置为1.4 s(并不代表实际工作时间)]:第一阶段,螺栓预紧,保持和现有的U-E密封压缩量设计方案一致,设置预紧位移为0.8 mm;第二阶段,充入40 MPa高压介质;第三阶段,排出高压介质,螺栓卸载,设置卸载位移为0.8 mm。

1.5 正交实验设计

U-E密封由于其复杂的横截面形式,涉及多种参数,主密封设计参数主要有密封悬臂长度、内张角和外张角;副密封设计参数主要有悬臂张角和厚度。每个结构设计5个变量,分别对主密封进行3因素5水平的正交试验设计、副密封进行全面试验设计,实验参数见表2。

表2 仿真实验对应水平编号Tab.2 Orthogonal experimental corresponding horizontal numbering

2 结果分析

2.1 法兰变形及主/副密封比压分析

法兰的倾斜变形直接导致U-E主/副密封面的密封比压存在较大差异,在仿真中将分为主密封正常和主密封失效两个情况进行,整个过程的时常设置为1.4 s,其中装配0.4 s,工作0.6 s,卸载0.4 s,分别考虑两种情况下的法兰变形量,法兰变形结果见图6。仿真结果表明:在主密封正常时主密封面位移紧随副密封位移,无位移滞后现象,在装配过程中(0～0.4 s)法兰并无明显变形产生。法兰充入40 MPa高压介质过程,充入介质总时长为0.6 s(0.4～1.0 s),由于设置光滑幅值曲线,压力随时间慢慢升高,主密封面与副密封面存在位移滞后现象,法兰的变形也逐渐明显,且在加压完毕时,上下法兰滞后距离达到最大,其值为0.156 mm,为法兰主/副密封的水平高度差。1.0～1.4 s时螺栓完全卸载,密封环受法兰压力作用,材料产生了永久塑性变形,导致法兰无法回到初始位置。

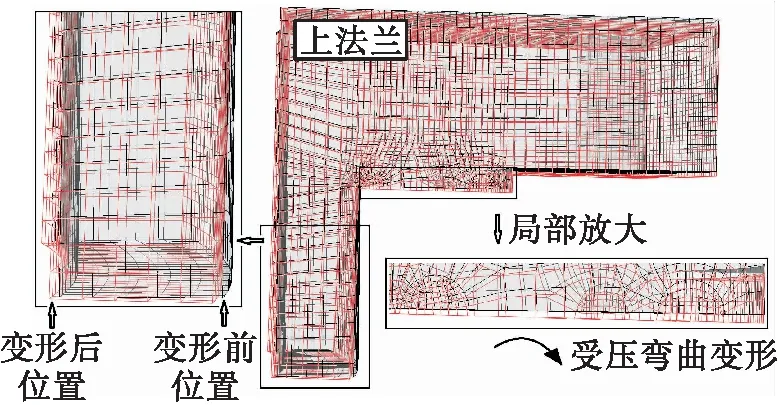
图6 上法兰仿真变形结果Fig.6 Simulated deformation results of upper flange structure

主密封发生泄漏,高压介质进入副密封区域,法兰受压面积增加,主密封自紧效应消失,副密封出现自紧效应,该情况下法兰主副密封面位移如图7所示,位移趋势和主密封未失效时保持一致。不同的是,在加压完毕后,上法兰的主密封面变形量增加了0.11 mm,副密封面变形量增加了0.07 mm;下法兰主密封面变形量增加了0.04 mm,副密封面变形量变化甚微。主密封面相对副密封水平高度差为0.23 mm。

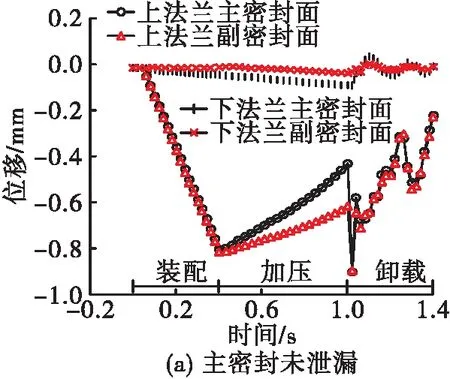
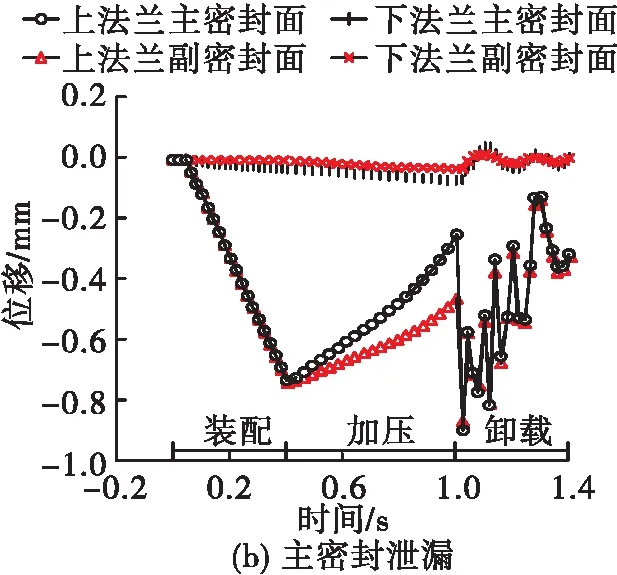
图7 密封面位移随时间变化(0.8 mm压缩量)Fig.7 Seal displacement variation with time (seal compression is 0.8 mm)

密封比压在仿真中用密封面接触压强(CPRESS)表示,密封的密封性能采用密封比压比来表示,即密封比压/介质压强。当密封比压比的值大于10时,认为该密封可靠。图8结果显示:在考虑了法兰变形的情况下,副密封面密封比压比在工作时(主密封泄漏)大于10,在冲压过程中最小为9.6,可认为副密封在介质压强为40 MPa时是可靠的。但是主密封在工作时(主密封未泄漏)密封比压比均小于10,密封不可靠,该主密封设计理论压缩量为0.8 mm,由于法兰的变形,实际压缩量只有0.7 mm,加压后压缩量为0.35 mm,远小于理论设计值。在后续结构设计中,需要考虑增大压缩量。

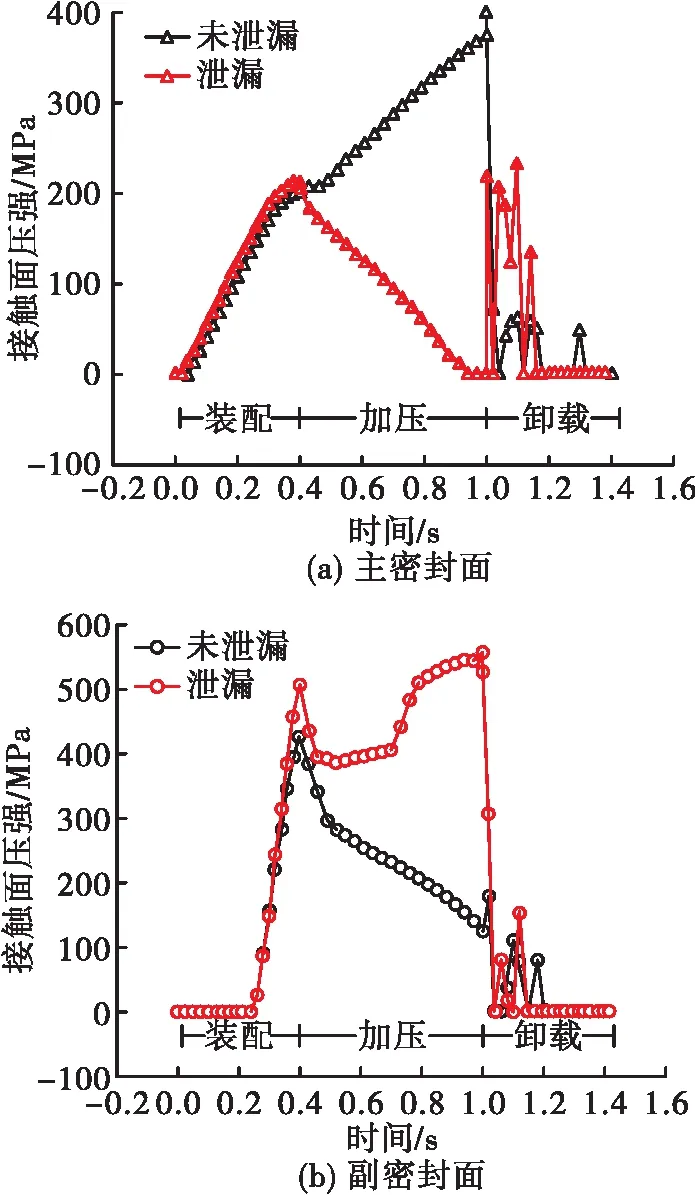
图8 密封比压随时间变化(0.8 mm压缩量)Fig.8 Specific-pressure of seal variation with time (seal compression is 0.8 mm)

综上所述,引入Walters法的法兰变形分析,在介质压强为40 MPa时,法兰倾斜变形使主/副密封面间存在0.16～0.23 mm高度差,导致U-E密封主/副密封比压不匹配,同时引起实际压缩量小于设计压缩量,导致主密封面密封比压不足。

2.2 U-E密封设计与仿真评估

法兰的变形引起主/副密封面产生高度差,设计U-E密封时,考虑由密封面的高度差引起的密封比压的变化。根据2.1节分析结果,法兰的变形使得实际压缩量小于设计压缩量,为增大压缩量,将设计压缩量从0.8 mm增加到1.2 mm;同时由于法兰的变形倾斜,将主/副密封面高度差设计为0.15 mm(见图9,h=0.15 mm)。

图9 主/副密封匹配设计示意图Fig.9 The schematic view of master and secondary seal matching design

通过对比正交实验密封面的密封比压,仿真结果表明:主密封外悬臂张角在14.4°～16.0°、内悬臂张角在20.0°～22.0°、密封悬臂长度在25.0～30.0 mm、副密封悬臂厚度在1.75～2.25 mm、悬臂张角在18.9°～23.1°内,密封比压均满足要求。由于密封比压不是越大越好,过大的密封比压容易导致密封环的压溃,最优结构的密封比压比需要大于10且接近10,故选取密封比压比为10.5的一组设计结构参数:α1=16.0°、α2=20.0°、L=25 mm、d=2.00 mm、β=21.0°。

增加压缩量为1.2 mm后的法兰变形如图10所示,主密封未泄漏时,法兰主副密封面高度差约0.25 mm;主密封泄漏后,法兰主副密封面高度差约0.28 mm;压缩量增加导致密封环支反力增加,法兰主/副密封面高度差随之增加。

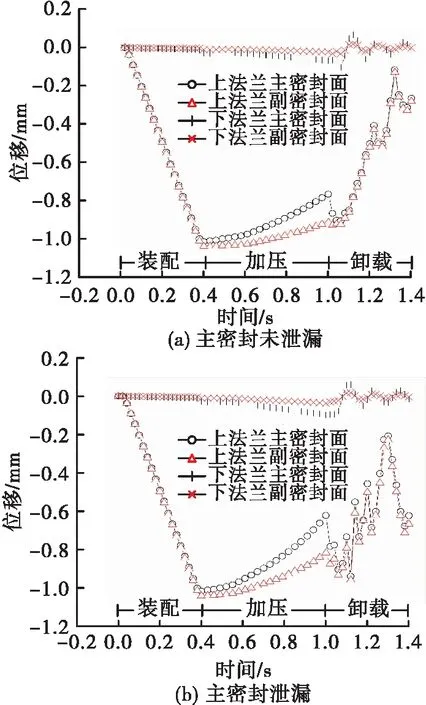
图10 密封面位移随时间变化(1.2 mm压缩量)Fig.10 Seal displacement variation with time (seal compression is 1.2 mm)

分别对比新/老结构的主/副密封面密封比压,具体结果见图11。对于老结构,在设计的时候,由于未考虑法兰变形,因此当法兰变形时,实际压缩量不足,导致密封比压不足;对于新结构,设计时候考虑了法兰变形和增加压缩量,因此增加压缩量后的密封环接触压强均有明显增加,由于压缩量增加程度大于主副密封高度差增加程度,所以主密封接触面压强增大了约66%,即262 MPa。副密封工作时接触面压强增大了约10%,即54 MPa。两者在工作时密封比压比均大于10,解决了老结构主密封密封比压不足的问题,同时也未将副密封密封比压增加很多,密封性良好。考虑了法兰的变形,根据主/副密封接触面压强,能够为U-E密封环主/副密封高度的设计提供参考。

图11 密封比压随时间变化Fig.11 Specific-pressure of seal variation with time

2.3 典型试验验证

对优化后的U-E密封环进行试验考核,试验结果见表3,20 MPa为1倍压力。在低压情况下,施加1.2 mm的压缩量,多次进行液压试验未出现泄漏情况;在高压情况下,施加1.2 mm的压缩量,多次进行试验未出现泄漏情况。此试验结果与仿真计算结果基本一致,这里需要说明的是,实际工作中密封面表面涂有软铜镀层,可以更好地提高密封性。

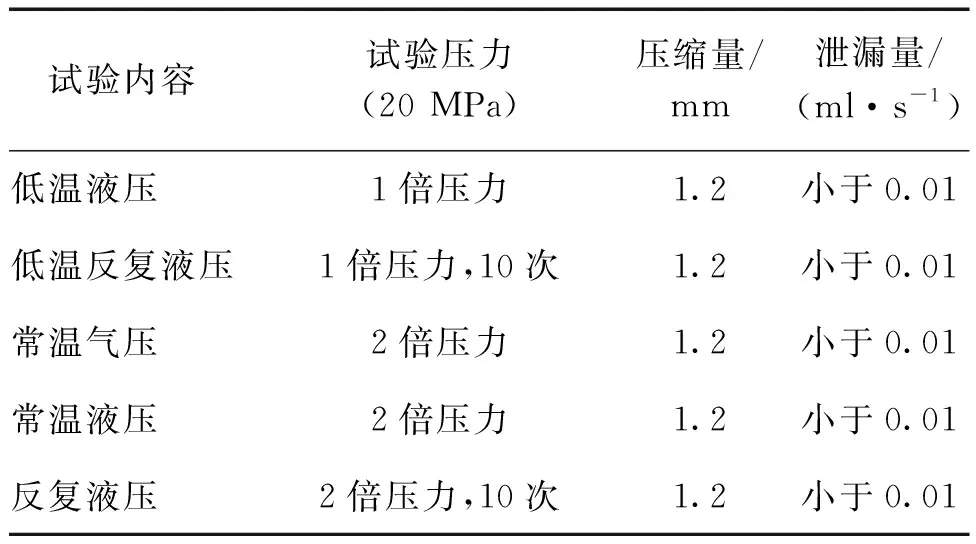
表3 U-E密封环试验结果Tab.3 Experiment results of U-E seal

3 结论

1)将法兰变形引入U-E密封环设计中,比将法兰视为刚体的密封环设计方法更加符合实际。采用Walters理论将法兰看作弹性梁,法兰螺栓结构为静定结构,通过理论分析结合三维仿真,得出法兰主/副密封面变形的大小。通过法兰变形将主/副密封之间的设计联系起来;对于U-E密封多参数设计问题,采用3因素5水平的正交实验进行设计分析;形成了一套系统性的优化设计方案。

2)基于Walters法,法兰在充入高压介质后产生变形导致U-E密封环的主/副密封面之间产生0.23 mm的高度差,并使得实际压缩量只有设计压缩量的44%,根据此结果,对U-E密封环的主/副密封结构进行了优化,将主/副密封高度差增大到0.3 mm;对密封压缩量进行了增加,将压缩量由0.8 mm增加到1.2 mm。重新对设计后的密封环进行三维仿真,其密封比压达到要求。

3)对改进后的密封环进行试验考核,通过了重复充泄压试验,最高压力为40 MPa,试验中密封环性能良好,显示了改进效果明显,验证了模型的正确性。