利用模态应变能变化率的结构损伤识别优化方法

缪炳荣 张盈 黄仲 张哲 杨树旺

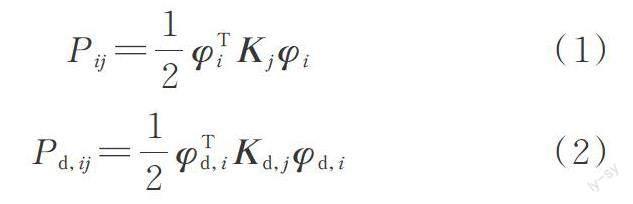
摘要 针对结构损伤识别过程中存在的定位精度和量化分析不足的问题，提出一种基于结构振动响应的模态应变能变化率与优化技术相结合的损伤识别方法。利用两步法确定可疑损伤单元及对其损伤程度进行量化分析。通过有限元法建立结构的损伤特征模型，且利用单元模态应变能变化率指标构建损伤指标优化分析的目标函数。数值分析过程中，利用粒子群优化算法与遗传算法对设计变量进行优化分析。同时比较模态应变能变化率与小波分析两种方法下的损伤定位的量化分析效果和识别效率。在实际算例中，利用梁结构进行损伤识别优化方法的结果验证。结果证明该方法能够显著提高结构振动损伤和定位的有效性。该方法不仅能够快速和精准地进行结构损伤量化分析，比小波方法具有更好的定位效果，而且能够提高量化分析的识别效率。但该方法在实施过程中的定位精度容易受到噪声的影响，通过优化目标函数可在一定程度上提高该结构损伤识别方法的抗噪能力。

关键词 损伤识别; 模态应变能; 小波变换; 有限元; 算法优化

引 言

轨道车辆在极端服役环境和各种不确定因素（振动、温度、湿度等）的影响下，其关键部件经常会产生振动疲劳和各种裂纹萌生及扩展的结构损伤事件。按照结构动力学理论，结构损伤识别（Structural Damage Identification，SDI）也称结构损伤检测（Structural Damage Detection，SDD），属于动力学正逆混合问题［1］。损伤定位和量化分析主要根据结构部件的振动响应（加速度、位移、应力应变信号等）求解系统的特征参数（固有频率、模态振型等）的变化。随着未来铁路智能运维策略的不断发展和实施，车辆与基础设施（线路、桥梁、隧道等）的结构振动损伤识别技术的工程应用需求已经变得十分迫切［2］。

小波方法由于具有多分辨率的特点，被很多学者应用于结构损伤识别过程中。一般方法是对结构模型的模态振型结果进行变换，通过小波系数的极值差进行结构的损伤定位与量化分析。但是小波方法在对结构振型数据分析时，由于边界条件等不确定因素的影响容易使得识别效果有时并不理想。小波方法是根据损伤导致结构模型产生细微不连续或振型的奇异特征进行损伤定位。但结构对称性和一些特殊模态节点位置（如约束位置）的存在也可能会影响到实际模型中损伤位置的识别。显然，仅仅使用结构振型参数与小波变换等方法对于结构的损伤定位和损伤程度的量化分析还存在一定的局限性。因此，许多学者也逐渐将多目标优化技术应用于结构损伤识别过程中，以改善对结构损伤位置与损伤程度的识别效果［2］。

另外，相对于利用结构振动频率、模态、柔度矩阵等损伤识别方法，模态应变能（Modal Strain Energy，MSE）方法近些年来因为其具有良好地反映结构的微小损伤信息的定位能力而备受许多学者的关注［3?9］。Wang等［3］对模态应变能相关指标的损伤识别方法进行了综述，对比分析了几种模态应变能的损伤识别算法。Seyedpoor［4］和Arefi等［5］讨论了两步法和MSE方法识别结构损伤的一些细节。刘文光等［6］利用弹性理论推导了弹性薄板的模态应变能，并构造损伤识别指标对固支弹性薄板结构的损伤进行定位分析。梁振彬［7］对基于模态应变能指标的损伤识别方法进行了较为系统的研究，通过梁、板、桁架等进行结果试验验证。卫军等［8］在模态应变能变化率（Modal Strain Energy Change Rating，MSECR）的基础上提出应用贝叶斯数据融合理论处理的损伤识别方法，以改进传统应变能方法的损伤识别能力。Fu等［9］采用模态应变能变化率确定板结构的损伤位置，并提出一种削弱损伤位置邻近效应的方法，减少定位过程中的虚假识别现象。同时，Wei等［10］基于响应灵敏度的有限元模型更新和应变能方法进行了损伤程度识别的优化求解。

如何利用结构振动响应数据构建结构损伤识别的优化目标函数进行算法优化也成为最近几年的研究热点。优化算法与损伤检测技术相互结合也能提高结构振动损伤识别方法的精度和效率［11?13］，但是在實际应用中依然存在一些局限性。Vo?Duy等［14］利用两步法和差分进化算法进行损伤识别目标函数的优化研究；另外，他们还提出基于应变能变形方法和差分进化算法（Differential Evolution，DE），且将其应用于多层复合板损伤的定位与量化分析［15］。Alexandrino等［16］采用多目标遗传算法求解结构损伤识别问题。Khatir等［17］以复合材料梁结构为对象，对比粒子群优化算法（Particle Swarm Optimization，PSO）和遗传算法（Genetic Algorithm，GA），发现PSO在损伤检测和定位上的识别效果优于GA，计算量更小，收敛速度更快且抗噪性更强。Hou等［18］基于灵敏度矩阵的最大独立性或最小互相关性的结构损伤识别方法，结合遗传算法进行结构损伤识别，取得较好的效果。Seyedpoor等［19］通过DE进化算法快速确定结构损伤的位置和损伤量，减少迭代步数且具有更高的识别精度。为了弥补差分进化算法求解维度过高容易导致定位损伤错误的缺点，Guedria［20］又提出一种改进的加速差分进化算法（Accelerated Differential Evolution，ADE）。Chen等［21］提出混合粒子群优化（Hybrid PSO，HPSO）的损伤识别方法，并通过蒙特卡罗算法验证其有效性。

从上述研究发现，模态应变能方法虽然可以利用损伤和无损伤结构的微小刚度改变的细微差异进行损伤定位。但是，仅仅依靠应变能的损伤识别方法依然存在识别精度低和计算成本高等问题，在处理多目标优化设计变量时量化识别效果也不理想。主要问题包括：

（1）结构损伤程度的量化分析不足且计算效率低。尽管应变能方法可以对损伤位置进行确定，并对损伤程度定性分析，但是对结构损伤程度进行量化分析的效率不高。

（2）基于结构振动响应的损伤识别均需要未损伤结构（健康结构）数据作为基线数据，而实验验证很难在多次测量中保证数据的一致性，因此要对仿真模型进行更新和修正。

针对上述应变能损伤识别方法存在的问题，本文将应变能方法与优化技术结合，构建模态应变能变化率损伤指标和优化目标函数，利用损伤指标进行损伤定位，使用多目标优化算法进行量化分析和提高计算效率，且利用数值仿真和实验验证技术验证结构损伤识别方法的损伤检测能力。该方法的提出主要是为了解决轨道车辆智能运维中结构损伤识别算法的完善问题，重点提高轨道结构裂纹识别的定位精度和量化分析能力。

1 理论背景和数学模型

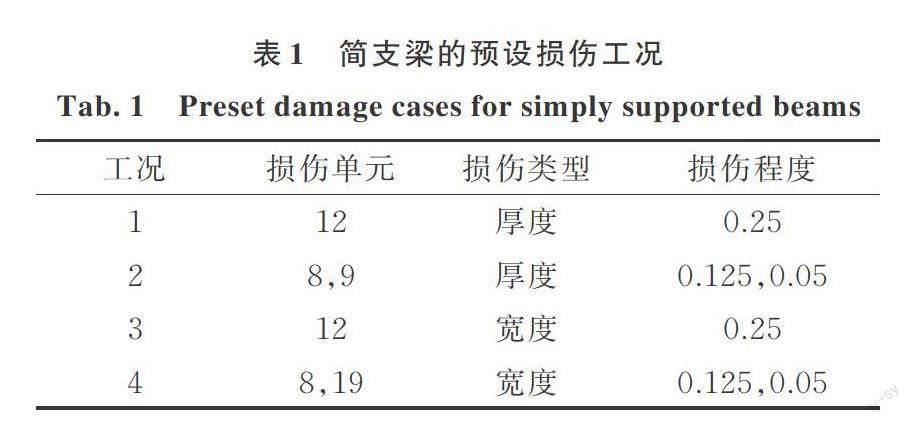
模态应变能方法主要通过结构刚度矩阵与模态振型次幂的乘积构造，结合结构振动特性与物理特性，在表征结构微小损伤方面具有独特的定位分析优势，且可以在一定测量噪声的环境下对微小损伤的结构进行有效的位置识别。结构无损伤和有损伤模态应变能可分别表示为［4?5］：

式中 下标“d”表示结构的损伤情况；Kd，j表示损伤单元j的单元刚度矩阵，按照整体坐标系扩展成新的刚度矩阵；φi和φd，i分别表示无损伤与损伤状态下结构的第i阶模态振型。

很多研究者都证明通过无损结构的刚度矩阵代替有损单元刚度矩阵后，单元模态应变能的损伤定位效果将更加明显［22］。结构系统中出现损伤时，添加一个微小扰动来建立结构振动方程，如下式所示：

式中 αj表示第j单元的损伤系数；cit表示第t阶振型的参与系数；m表示参与计算的模态总数；L表示结构的单元总数；λi和Δλi分别表示第i个特征值和第i个特征值的扰动值；φi和Δφi分别表示第i阶振型和第i阶振型的扰动值。

经过计算可得MSE的变化量：

式中 单元刚度矩阵Kq和Kj扩展到与整体刚度矩阵相同的维数，除了与单元q和单元j自由度对应的元素外，其余位置处均为0。λr和λi分别代表第r和i个特征值；φi和φr分别表示第i阶振型和第r阶振型的扰动值。

当j=q时，即单元q为损伤单元，则向量φTrKq 和Kjφr 的非零元素完全对应，使得模态应变能值变化最大；当j≠q，但单元j与单元q相邻，两个单元有部分公共自由度时，向量φTrKq和Kjφr的非零元素部分对应，模态应变能变化值较大；当j≠q，但单元j与单元q相距较远时，向量φTrKq和Kjφr的非零元素完全不重合，模态应变能的值变化将很小。由此，便可通过结构的模态应变能的变化来进行结构损伤单元的诊断。

本文中将采用模态应变能变化率进行梁结构损伤的定位研究。第j个单元的模态应变能变化率定义如下：

式中 Qij=ΔPij/Pij=|Pd，ij?Pij|/Pij，Qmaxij表示Qij中的最大值。

2 结构振动损伤识别优化算法

近些年来，优化算法在结构损伤识别的研究中应用普遍，常见方法是利用优化算法修正模型的参数或边界条件，保证仿真与实验模型尽可能保持一致，从而提高结构损伤位置和程度的识别精度和效率［14，17］。换言之，可以采用优化目标函数（常定义为实验模型与数值模型数据之间的差异）描述单元受损程度的指标。

2.1 损伤识别优化算法流程

本文选取3种目标函数分别与粒子群和遗传算法相结合，进行梁结构损伤识别的优化研究。具体算法包括以下两步：

步骤1：利用模态应变能方法完成损伤单元的初步定位。

（1）建立结构损伤前后的有限元数值模型，进行计算模态分析，获得结构振动响应数据；

（2）计算损伤结构与无损伤结构的单元模态应变能。假设损伤结构单元刚度未知，使用无损伤结构单元刚度矩阵代替损伤结构的刚度矩阵进行计算；

（3）计算单元损伤前后的各阶模态应变能变化率及前几阶平均模态应变能变化率；

（4）按照设定的可疑损伤单元的安全阈值分析可疑损伤单元，完成损伤单元的初步定位。

步骤2：结合多目标优化技术和两种优化方法对可疑结构损伤进行量化分析。

（5）将确定的可疑损伤单元的损伤程度设为一组损伤向量，将损伤量化问题转化为迭代寻优问题；

（6）以损伤向量为变量构建用于优化迭代的计算模型，进行模态分析，获取其振动响应数据；实验过程中，计算模型需要利用未损伤结构响应数据进行模型修正；

（7）结合计算模型与损伤模型的响应数据，构造损伤量化的目标函数；

（8）将目标函数值转化为优化算法所需的适应度值；

（9）利用优化算法进行损伤向量的寻优迭代，直至满足循环终止条件，产生最优损伤向量，最终完成损伤单元的准确定位与程度量化。

利用结构振动的损伤识别优化算法如图1所示。

2.2 损伤识别优化目标函数

使用优化算法进行结构的损伤识别的研究，很多学者已經提出了很多方法［5，8，14?22］。主要包括两种：一是直接利用模型振动响应的实测与仿真数据构建优化算法目标函数，通过目标函数的最小化确定损伤特征参数；二是直接比较实测与仿真模型的模态保证准则（Model Accurate Criterion，MAC）数据。本文直接利用模型振动响应的仿真与实测数据，将梁的损伤位置和损伤程度的量化分析问题转化为多目标函数的优化问题，其目标函数和设计变量及边界条件如下式所示：

式中 F=f（J1，J2，J3）为J1，J2，J3的优化目标函数；x=[x1，x2，…，xn]为损伤变量，且包含可疑单元的损伤位置信息；n为可疑损伤单元的个数；Yindex表示损伤量化指标；Ythreshold表示量化指标的安全阈值；k和kmax分别表示优化循环的迭代次数及上限值。

三种优化目标函数如下式所示：

式中 NF，NM和NP分别表示固有频率、模态振型和模态节点的数量j的最大值；上标“E”和“C”分别表示实测和数值计算数据；ω表示结构的频率；φ表示结构的振型；W表示响应的权重系数；上标“T”表示矩阵的转置。

3 数值算例

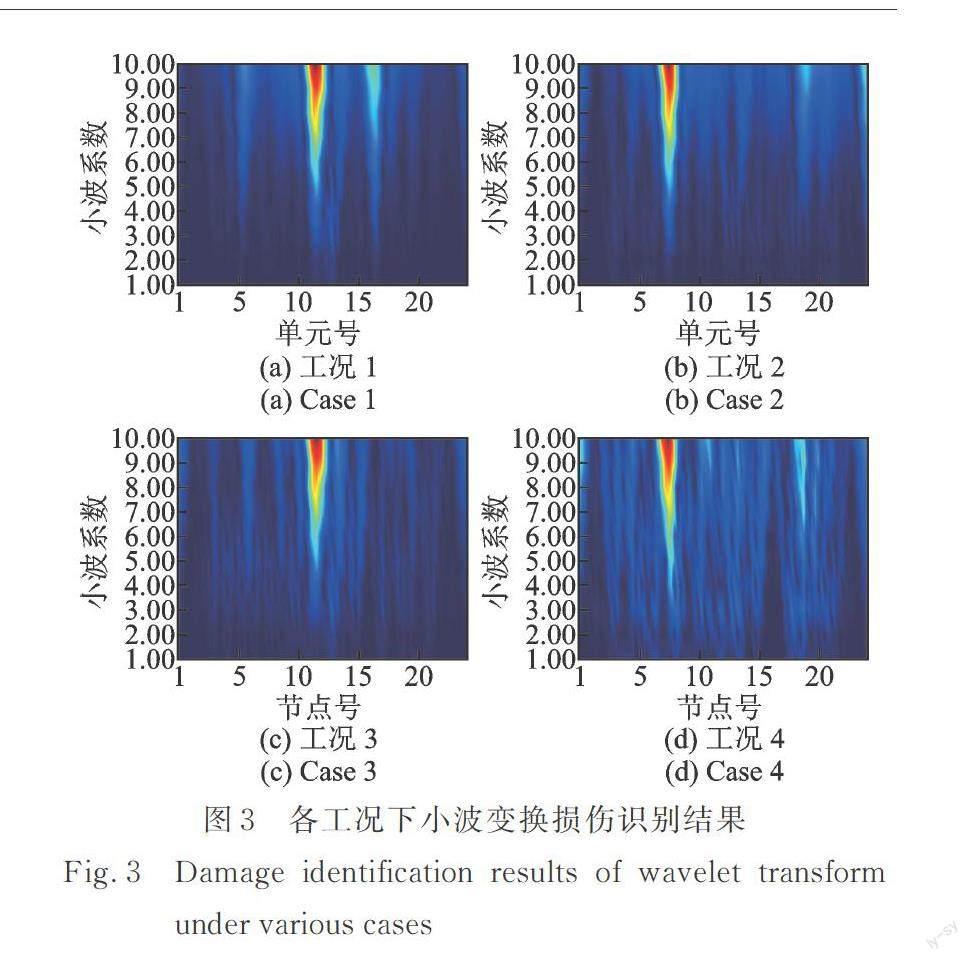
本文以简支梁结构为对象，进行损伤识别的定位和损伤程度的量化研究。简支梁数值如图2所示。该简支梁长宽高尺寸为1200×60×4 mm3。材料为Q235钢，弹性模量E=2.06×1011 Pa，泊松比为ν=0.3。通过有限元建模，将梁沿长度方向均分为24个单元，图中圆圈内数字表示单元号，梁下方数字表示节点号，红色单元表示损伤。设定的损伤工况如表1所示。

3.1 结构损伤定位

首先对简支梁在不同工况下的损伤进行定位分析。根据梁结构有限元模型计算获得的模态振型数据进行三次B样条线性插值后作小波分析，以初步确定损伤位置。小波变换结果如图3所示。通过分析可以发现，小波变换系数的模极大值基本都出现在预设损伤位置，可以较为准确地进行损伤单元的定位。但损伤形式、数量以及损伤位置和程度对于同一小波基函数下的小波变换结果有较大影响。图3（a）所示的损伤识别结果出现了两条较为明显的虚假损伤信息。其余各工况下，尽管未出现较明显的损伤误报，但也存在较多的损伤干扰特征。

本文将模态应变能变化率值大于所有单元中最大值的20%的单元设定为可疑损伤单元。在各计算工况下，通过建立有限元模型和模态分析，利用模态振型的输出结果计算简支梁结构的模态应变能变化率。利用模态应变能变化率的损伤位置的识别结果如图4所示。分析结果发现，每种损伤工况下提出的方法均可以有效识别损伤单元的位置，损伤识别指标没有受到结构损伤类型、位置及数量的明显影响。利用模态应变能变化率的结构损伤识别方法的定位稳定性优于小波方法的位置识别结果。

通过小波变换与模态应变能变化率两种方法分别进行简支梁损伤识别的结果如表2所示。虽然这两种方法都能够识别各工况下所有真实的损伤单元，但利用模态应变能变化率的损伤识别方法对于可疑损伤单元的数量更少，并且损伤定位识别效果更明显。

3.2 损伤识别量化

利用结合模态应变能变化率与优化技术提出的损伤识别方法对梁结构的损伤程度进行了量化分析。为了分析此方法对梁结构损伤量化的效果，本文利用遗传算法（GA）与粒子群优化（PSO）算法结合三种目标函数，对可疑损伤单元进行损伤程度的量化对比分析。两种优化算法的参数设置如下：GA的种群大小为30，最大遗传代数为50代，个体的二进制编码长度为20，交叉概率为0.8，变异概率为0.01；PSO算法的种群规模也为30，最大进化次数仍然为50，速度变化范围从-0.15至0.15。两种优化算法的结构损伤识别结果如表3所示。

从表3中可以发现，目标函数J2在期望的迭代计算步数内均可以达到最优解。但两种优化方法识别的结构损伤程度与预设结果稍有差异。目标函数J1和J3在可疑损伤单元较少的情况下，损伤程度的量化较为准确，但当需要识别的可疑损伤单元较多，且含有对称单元时，目标函数J1的优化结果出现较大偏差，目标函数J3在各工况下的损伤程度优化结果均表现良好。损伤形式、损伤位置以及可疑损伤单元的数量对于以目标函数J3进行损伤程度优化的结果并不产生明显的影响。整体说，PSO算法与GA算法在可疑单元较少时的优化结果相差无几，均能实现误差2%以内的损伤程度识别，识别结果中，粒子群优化算法的结果略优于遗传算法。两种优化算法利用目标函数J3进行的部分工况优化历程如图5所示。可以发现在优化迭代计算过程中，粒子群优化算法比遗传算法能够更快地收敛到满足精度要求的结果，并且粒子群算法的适应度值更小。

3.3 损伤识别的抗噪分析

简支梁各节点自由度的损伤灵敏度如图6所示。由于各节点自由度对于单元损伤的敏感程度不同，为减少在实际测量过程中的工作难度，提高效率，选择对损伤较为敏感的自由度将其定义为主自由度，其余自由度为从自由度，进行模态缩减。不同水平的随机噪声下结构损伤定位的表达式如下：

式中 φn是含有噪声的模态振型；φ为无噪声的模态振型；Eφ为噪声水平；τ表示标准正态分布向量；σ（φ）为无噪声数据的标准差。

式中 ωn为含噪声的频率数据；ω为无噪声的频率数据；rand为随机白噪声。

4个工况的分析结果如图7所示。其中，无噪声的数据结果是利用经验模态缩减后的结构响应计算得到的损伤定位效果。

由上述结果可以发现，利用模态缩减后的结构振型进行损伤定位是可行的，其识别结果与利用全自由度识别的结果相差不大。当在缩减后的响应数据中加入5%水平的随机噪声后，可疑损伤单元的数量明显上升，而将预设损伤位置的定位指标确定为模态应变能变化率后，可疑损伤单元的数量也明显降低。

另外，将各条件下的模态应变能变化率值大于该条件下模态应变能变化率最大值的20%的单元确定为可疑损伤单元，进行损伤程度量化。由于目标函数J1和J2在无噪声情况下的损伤识别的量化结果不理想，故本文仅利用目标函数J3进行损伤程度的量化比较。可疑损伤单元的损伤程度量化效果如图8和9所示。

从图8和9中可以看出，当可疑损伤单元较少时，基于目标函数J3的遺传算法和粒子群算法在预期代数内均能够成功判别损伤单元与未损伤单元，准确识别损伤程度。但当可疑损伤单元增加后，遗传算法的识别效果迅速恶化，甚至无法得到有效结果，而粒子群算法的稳定性较好，虽然随噪声水平的增加，识别精度和收敛速度有所下降，但其识别误差均未超过10%，且均能在50步内实现损伤程度的准确量化。各工况条件下的粒子群算法的损伤程度识别结果如表4所示。

4 试验结果对比验证

4.1 试验方案的设计

试验方案采用与仿真阶段相同材质和尺寸的简支梁。实验设备包括DH5923N信号采集器、DHDAS动态信号采集分析系统、笔记本电脑一台、DH131E型IEPE压电式加速度传感器2个和LC02型力锤，如图10所示。为降低加速度传感器的附加质量对梁结构振动造成的不利影响，采用单点输入?多点输出（SIMO）的振动测试方式，通过布置传感器测量梁结构的振动模态信息。

4.2 结果分析与讨论

在实验阶段采用的梁结构，主要包括两处损伤：第一处损伤位于第8和第9号节点之间，梁厚度由4 mm减少为2.47 mm；第二处位于第19和第20号节点之间，梁截面的厚度由4 mm减少为3.17 mm，主要用于表示刚度缺失。同时，利用模态误差极小扩阶法对损伤梁结构进行振型扩展和损伤诊断，其结果如图11所示。利用粒子群算法进行可疑损伤单元的损伤程度量化分析结果如图11（b）所示。简支板梁的真实损伤确定为第8与第19号单元，损伤程度的数值模型分别设定为38%和21%，而通过实验获得的损伤程度分别为46%和24%，识别误差分别为21.44%和12.14%，误差较大。对于未损伤的第5和第20号单元也未能正确地收敛至零。这是由于在结构模态测试的过程中，跨度较大的梁结构的模态容易受到外界振动的影响，较难获得良好光滑的振型数据结果。5号单元与8号单元接近，20号单元与19号单元邻近，其损伤程度的轻微变化可能导致仿真结构的优化振动响应与真实损伤结构的振动响应相匹配。这也是导致整体的损伤量化结果存在误差的原因之一。

从图11中可以发现，利用模态应变能变化率指标进行损伤定位时，由于测量过程中的噪声干扰、模型误差及边界条件因素的影响，结构损伤定位效果降低，损伤定位过程中可疑损伤单元较多。但是从损伤量化识别分析结果看，本方法在保证定位精度的前提下是可以有效进行损伤定位与量化分析的。

损伤阈值是表征结构损伤程度的重要参数变量的最大限定值，该值大小的设定与损伤指数的均值和标准差相关。由于振动响应可能会引起材料与结构内部或表面的局部变形和裂纹萌生、裂纹扩展甚至断裂破坏等，这就需要考虑结构在不同振动响应下的损伤程度，确定结构损伤阈值的设定问题。对于本文的研究而言，阈值的设置主要与潜在的结构损伤位置相关，其设定主要是参考文献［23］。这里将假设值大于0.15的归一化损伤指数值作为阈值设定，小于文献［23］中的阈值2。从一定程度上说，本文提出的方法要比文献中提出的阈值要求更高一些。

5 结 论

本文以简支梁为对象，提出一种结构单元模态应变能变化率与优化算法相结合的结构损伤识别方法。相关结论如下：

（1）提出的方法不仅可以充分利用模态应变能变化率的损伤识别方法的定位优势，且利用优化算法提高了其损伤识别的量化指标分析效果。同时，也发现基于模态应变能变化率方法比小波方法的损伤定位指标的识别效果更好。

（2）对不同噪声水平下梁结构典型损伤工况进行损伤定位及量化分析，发现仅仅依靠模态应变能变化率方法的识别结果的抗噪能力稍差。但是通过与不同的优化技术相结合，不仅可以提高损伤定位过程中的抗噪性，也在一定程度上解决其损伤程度量化分析不足的难题。

（3）结合简支梁结构损伤识别的实验验证结果可以看出，现场测试环境的噪声和一些边界条件的不确定性等因素，依然是提高損伤识别技术精度和效率面临的难题。

参考文献

1DAS S， SAHA P， PATRO S K. Vibration-based damage detection techniques used for health monitoring of structure： a review［J］. Journal of Civil Structural Health Monitoring， 2016， 6（3）： 477-507.

2YOKOYAMA A. Innovative changes for maintenance of railway by using ICT?to achieve “smart maintenance”［J］. Procedia CIRP， 2015， 38： 24-29.

3WANG Shuqing， XU Mingqiang. Modal strain energy-based structural damage identification： a review and comparative study［J］. Structural Engineering International， 2019， 29（2）： 234-248.

4SEYEDPOOR S M. A two stage method for structural damage detection using a modal strain energy based index and particle swarm optimization［J］. International Journal of Non-Linear Mechanics， 2012， 47（1）： 1-8.

5AREFI S L， GHOLIZAD A， SEYEDPOOR S M. Damage detection of structures using modal strain energy with Guyan reduction method［J］. Journal of Rehabilitation in Civil Engineering， 2020， 8（4）： 47-60.

6刘文光， 颜龙， 郭隆清. 基于模态应变能法的弹性薄板损伤识别［J］. 噪声与振动控制， 2016， 36（3）： 164-168.

LIU Wenguang， YAN Long， GUO Longqing. Damage identification of elastic thin plates by modal strain energy method［J］. Noise and Vibration Control， 2016， 36（3）： 164-168.

7梁振彬. 基于模态应变能的结构损伤识别方法研究［D］. 北京： 清华大学， 2017.

LIANG Zhenbin. Study on damage detection of structures based on modal strain energy［D］. Beijing： Tsinghua University， 2017.

8衛军， 杜永潇， 吴志强， 等. 基于模态应变能和Bayes理论的梁结构损伤识别［J］. 铁道科学与工程学报， 2019， 16（8）： 2052-2061.

WEI Jun， DU Yongxiao， WU Zhiqiang， et al. Damage identification of beam structures based on modal strain energy and Bayesian data fusion theory［J］. Journal of Railway Science and Engineering， 2019， 16（8）： 2052-2061.

9FU Y Z， LIU J K， WEI Z T， et al. A two-step approach for damage identification in plates［J］. Journal of Vibration and Control， 2016， 22（13）： 3018-3031.

10WEI Z T， LIU J K， LU Z R. Damage identification in plates based on the ratio of modal strain energy change and sensitivity analysis［J］. Inverse Problems in Science and Engineering， 2016， 24（2）： 265-283.

11JANELIUKSTIS R， RUCEVSKIS S， WESOLOWSKI M， et al. Experimental structural damage localization in beam structure using spatial continuous wavelet transform and mode shape curvature methods［J］. Measurement， 2017， 102： 253-270.

12RUCEVSKIS S， JANELIUKSTIS R， AKISHIN P， et al. Mode shape‐based damage detection in plate structure without baseline data［J］. Structural Control and Health Monitoring， 2016， 23（9）： 1180-1193.

13YANG H C， XU F Y， MA J X， et al. Strain modal-based damage identification method and its application to crane girder without original model［J］. Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science， 2019， 233（4）： 1299-1311.

14VO-DUY T， HO-HUU V， DANG-TRUNG H， et al. A two-step approach for damage detection in laminated composite structures using modal strain energy method and an improved differential evolution algorithm［J］. Composite Structures， 2016， 147： 42-53.

15VO-DUY T ， HO-HUU V， DANG-TRUNG H， et al. Damage detection in laminated composite plates using modal strain energy and improved differential evolution algorithm［J］. Procedia Engineering， 2016， 142： 182-189.

16Alexandrino P S L， Gomes G F， Cunha Jr S S. A robust optimization for damage detection using multi-objective genetic algorithm， neural network and fuzzy decision making［J］. Inverse Problems in Science and Engineering， 2020， 28（1）： 21-46.

17KHATIR S， BELAIDI I， KHATIR T， et al. Multiple damage detection in composite beams using particle swarm optimization and genetic algorithm［J］. Mechanics， 2017， 23（4）： 514-521.

18HOU R R， XIA Y， XIA Q， et al. Genetic algorithm based optimal sensor placement for L1‐regularized damage detection［J］. Structural Control and Health Monitoring， 2019， 26（1）： e2274.

19SEYEDPOOR S M， NOPOUR M H. A two-step method for damage identification in moment frame connections using support vector machine and differential evolution algorithm［J］. Applied Soft Computing， 2020， 88： 106008.

20GUEDRIA N B. An accelerated differential evolution algorithm with new operators for multi-damage detection in plate-like structures［J］. Applied Mathematical Modelling， 2020， 80： 366-383.

21CHEN Z P， YU L. A new structural damage detection strategy of hybrid PSO with Monte Carlo simulations and experimental verifications［J］. Measurement， 2018， 122： 658-669.

22繆炳荣， 刘俊利， 张盈， 等. 轨道车辆结构振动损伤识别技术综述［J］. 交通运输工程学报， 2021， 21 （1）： 338-357.

MIAO Bingrong， LIU Junli， ZHANG Ying， et al. Review on structural vibration damage identification technology for railway vehicle［J］. Journal of Traffic and Transportation Engineering， 2021， 21（1）： 338-357.

23CORNWELL P， DOEBLING S W， FARRAR C R. Application of the strain energy damage detection method to plate-like structures［J］. Journal of Sound and Vibration， 1999， 224（2）： 359-374.

Structural damage identification optimization method using change rate of modal strain energy

MIAO Bing-rong ?ZHANG YingHUANG ZhongZHANG ZheYANG Shu-wang

State Key Laboratory of Traction Power， Southwest Jiaotong University， Chengdu 610031， China

Abstract According to the problem of insufficient positioning accuracy and quantitative analysis in the process of structural damage identification， this paper proposes a damage identification method based on the combination of structural vibration response-based Modal Strain Energy Change Rate （MSECR） and optimization technology. Firstly， a two-step method is used to determine the suspicious damage unit and quantitatively analyze its damage degree. The finite element method is applied to establish the damage characteristic model of the structure， and the element modal strain energy change rate index is used to construct the objective function of the damage index optimization analysis. In the process of numerical analysis， Particle Swarm Optimization Algorithm （PSOA） and Genetic Algorithm （GA） are used to optimize the design variables. At the same time， the quantitative analysis effect and identification efficiency of the damage location of the two methods of modal strain energy change rate and wavelet analysis are compared. In actual calculation examples， the beam structures are used to verify the results of the damage identification optimization method. The results show that this method can significantly improve the effectiveness of structural vibration damage and positioning. This method can not only perform quantitative analysis of structural damage quickly and accurately， but also has a better positioning effect than the wavelet method. And it can improve the identification efficiency of quantitative analysis. However， it is also found that the positioning accuracy of this method in the implementation process is easily affected by noise. The optimization of the objective function can improve the anti-noise ability of the structural damage identification method to a certain extent. The research of this method will provide certain technical guarantee for the practical engineering application of the damage identification algorithm in the future railway intelligent operation and maintenance.

Keywords damage identification; modal strain energy; wavelet transform; FEM; algorithm optimization