应用Python-GPU求解的实时混合试验方法研究

董晓辉 唐贞云 李振宝 杜修力

摘要 提出了基于Python和图形处理器（GPU）数值求解的实时混合试验系统。将土?结相互作用系统作为试验模型，使用Python?GPU代替CPU数值求解，对提出的实时混合试验系统进行了仿真与试验验证。研究结果表明，使用Python?GPU对无条件稳定算法求解，积分步长20 ms时GPU实时求解模型自由度超过24000，是同一台计算机CPU求解规模的7倍左右，提升了实时混合试验的试验能力。

关键词 实时混合试验; 图形处理器; Python; 数值积分算法; 求解效率

引 言

实时混合试验［1］是一种将数值仿真与物理试验相结合的试验方法，将试验结构分为数值子结构与物理子结构，两部分数据实时交互传输，使得大型复杂结构大比例试验成为可能，现已得到广泛应用。在实时混合试验中，数值子结构动力求解需在一个时间步长内完成，数值子结构模型自由度越高，求解耗时越大。过大的时间步长影响数值积分算法的精度及物理子结构加载的准确性，无法满足实时混合试验的需要。在数值子结构动力分析过程中通常采用计算效率更高的显式积分算法进行求解，显式积分算法（例如中心差分法）通常为条件稳定算法，积分步长越小精度越高［2］。过小的步长限制了数值模型实时求解规模，难以实现大规模数值模型的实时求解［3］。为解决此问题众多学者在改进数值积分算法［3］及提升数值子结构计算效率［4］等方面做出研究。

在改进数值积分算法的研究中，Nakashima等［5］及Chang［6?7］分别提出拟动力试验的无条件稳定显式积分算法，但这些方法在实时混合试验中为隐式算法。吴斌等［8］基于上述方法进行研究，利用位移向前差分修正建立实时混合试验中无条件稳定的显式积分Chang算法。Chen等［9］基于离散控制原理和极值的概念提出CR法，在线性结构和部分非线性系统中具有无条件稳定性，且速度和位移均显式。Tang等［10］基于运动方程离散化提出TL算法，在线性结构系统中具有无条件稳定性，且速度和位移均显式表达。基于现有的动力分析算法，在提升实时混合实验数值子结构计算效率方面也有众多学者研究。Nakashima等［11］提出Digital Signal Processor（DSP）方法，在一个时间步长内完成数值模型仿真和动力响应信号处理，实现了10自由度模型330 ms时间步长或12自由度模型500 ms时间步长的实时混合试验。Chae等［12］开发Hybrid FEM程序，实现514自由度框架模型10 ms时间步长的实时混合试验。Zhu等［13］提出使用两台目标计算机的实时混合试验D?RTHS系统提升求解规模，实现超过1240自由度时间步长为20 ms的实时混合试验。Lu等［14］在D?RTHS系统的基础上结合计算机并行計算提出RTHS?W系统，使用条件稳定的中心差分法实现时间步长为20 ms条件不超过7000自由度（Rayleigh阻尼β≠0）或40602自由度（Rayleigh阻尼β=0）模型的实时混合试验。综上所述，通过改进实时混合试验数值求解算法及求解的方法，可以提升数值子结构模型实时求解能力，但目前的求解规模仍在7000以内（Rayleigh阻尼β≠0）。

在实时混合试验中，数值子结构求解通常基于计算机的中央处理器（CPU）运算，然而在进行大量数据运算时，CPU的计算能力难以满足模型实时求解的需要。图形处理器（GPU）芯片与CPU的架构不同，GPU中有数倍于CPU的计算单元，在进行大规模数值计算时GPU具有明显优势。在土木工程领域，GPU的高性能求解已得到应用。刘晓强［15］应用GPU提升大规模数据绘制和拓扑分析性能，实现相比CPU数十倍的加速效果，满足土木工程领域防灾减灾数据可视化需求。解琳琳等［16］应用GPU加速OpenSees有限元仿真，对城市地震灾害进行模拟，实现相比CPU计算39倍的加速效果。在实时混合试验研究方面，董晓辉等［17］已应用MATLAB软件实现GPU求解数值子结构，基于GPU求解实时混合试验架构并验证其性能，证明了应用GPU求解数值模型可以提升试验模型规模，降低时间步长。在MATLAB?GPU实时混合试验系统架构中，使用GPU加速条件稳定的显式算法求解，并且子结构之间通讯存在3 ms的延迟。为解决上述问题，本文提出使用Python编程建立基于GPU计算的实时混合试验系统，优化基于GPU求解的实时混合试验系统，以土?结相互作用系统为模型进行振动台实时混合试验，测试架构的可行性及性能。

1 试验系统组成

在基于Python?GPU求解的实时混合试验系统中，使用GPU代替CPU作为数值模型求解的硬件。为了实现数值模型的高效仿真及数据实时交互，试验系统如图1所示，分为三个部分：数值子结构部分，信号处理部分和试验子结构部分。

1.1 数值子结构部分

数值子结构部分负责数值模型实时动力分析，在此部分使用Python作为编程语言编写动力求解算法，调用CuPy函数库实现GPU运算［18］。在模型仿真程序中添加UDP网络通讯模块［19］，实现基于GPU的模型动力求解与试验子结构实时通讯。

1.2 信号处理部分

信号处理部分负责固定数值子结构求解的时间步长，信号插值以及振动台控制补偿。在实时混合试验中，数值子结构快速且准确的求解是试验成功的关键，试验的时间步长需要保持固定不变。由于数值模型仿真在非实时系统Windows［20］上运行，每一步数值模型求解所用的时间不固定，对此需要保证每一步模型时间步长固定且求解耗时均小于时间步长。控制时间步长可以通过LabVIEW等软件的定时循环或在数值求解计算机外添加实时硬件。

本文在两个子结构之间添加Simulink Realtime xPC（下文简称xPC）实时硬件，xPC实时硬件有较好的实时性［21］，可以实现50 kHz的实时仿真，即可以实现最小时间步长为2×10-5的实时仿真，能满足实时混合试验最小时间步长为1×10-3的要求。在xPC中添加UDP网络通讯模块［22］，连接数值子结构与试验子结构；添加信号插值模块，对数值子结构动力响应的离散信号进行插值，使得输入试验子结构的信号指令更平滑。为降低试验子结构加载装置的加载误差，在xPC中添加FSCS补偿控制器［23］。完成插值及补偿后，xPC将信号通过UDP传输至试验子结构。

1.3 试验子结构部分

试验子结构部分与基于CPU的实时混合试验方法相同，通过物理加载的方法对试件试验。加载装置的控制器接收到数值子结构响应后，对试验试件加载。在试验试件上布置加速度及位移传感器，将时程响应传输至加载系统控制器采集，再通过加载系统控制器将试件响应反馈至数值子结构。

2 基于Python的GPU求解性能

Python作为一种解释型编程语言具有丰富的拓展库，适用于各種系统平台，随着版本的不断更新和语言新功能的添加，被广泛应用于科研领域。CuPy［18］是一个借助CUDA实现GPU加速的Numpy格式数据运算库，可以利用GPU的众多CUDA核心提升数值计算效率。本文选择Python作为编程语言，实现基于CuPy函数库的数值子结构模型GPU实时求解。

2.1 实施方案

使用Python进行数值模型动力求解需要建立数值子结构动力方程，模型的质量、刚度和阻尼矩阵需要借助有限元软件前处理得到。本文选择使用ABAQUS有限元软件建立数值子结构模型，调整划分网格完成模型前处理，添加模型参数矩阵输出脚本，得到数值子结构模型的质量和刚度矩阵，模型阻尼采用Rayleigh阻尼。将模型的质量、刚度、阻尼参数矩阵导入Python中建立结构动力方程。

使用CuPy库进行GPU加速计算前，将CuPy库添加至数值子结构求解的程序中，并将模型及算法所需的参数通过cupy.asarray函数转换为CuPy数据格式［18］。为实现数值子结构与试验子结构之间数据交互，完成模型动力分析后使用cupy.asnumpy函数将界面响应转换为Numpy数据格式，在每一步长动力分析前后添加UDP通讯脚本，并在xPC软件环境和试验子结构部分中配置好UDP端口实现网络通讯。使用Python?GPU进行实时混合试验时，数值子结构部分流程如图2所示。

2.2 仿真参数及配置

为验证本文提出的Python?GPU求解数值模型方法的可行性与性能，采用如图3所示的土?结相互作用模型作为算例，其中上部结构为试验子结构，下部土体为数值子结构。数值子结构动力分析分别使用条件稳定的中心差分法和无条件稳定的Newmark?β算法。试验子结构为单自由度铝框架，质量ms=14.5 t，刚度ks=10.03 kN/mm，阻尼cs=3.74 kN/（m?s?1），与数值子结构顶部中心锚固连接。数值子结构模型尺寸为30 m×30 m×15 m，密度为2.15×103 kg/m3，弹性模量为7.2×106 Pa，泊松比为0.35，阻尼比为0.05，模型四周及底部节点添加弹簧阻尼器模拟远场土边界条件，节点法向弹簧刚度为20000 N/m，切向为10000 N/m，法向阻尼器阻尼为1.437×106 N/（m?s?1），切向为9.45×106 N/（m?s?1）。数值模型在ABAQUS有限元软件中建模，每个节点有三个自由度，通过调整网格划分的间距调整模型的求解规模，网格越密，动力求解计算量越大。仿真中模型荷载为Kobe地震波，加速度幅值调整为0.5g。仿真中使用GPU服务器作为求解计算机，软件与硬件环境如表1所示。本文研究选择的土?结相互作用模型仅为了验证Python?GPU求解的可行性与计算效率。使用Python?GPU的数值模型求解方法不限于本研究中的线弹性模型与模型边界条件，适用于任何形式的实时混合试验。

2.3 仿真结果

数值子结构求解的GPU计算机与物理子结构仿真xPC之间通过UDP网络连接，数据传输需要时间。为了测试UDP网络通讯耗时在实时混合试验一个时间步长内的占比，使用GPU计算机通过UDP网络向xPC硬件发送数据10000次，计算单次UDP通讯耗时。使用Python中的time函数统计总耗时为0.078 s，平均单次通讯耗时为0.078/10000=7.87×10-3 ms，当实时混合试验时间步长为1 ms时，UDP通讯耗时的占比为0.79%。使用UDP网络传输数据的耗时在一个时间步长内可以忽略不计。

为了测试GPU求解数值模型的精度与性能，分别选取自由度为2592，5400，10830以及24375的模型，时间步长为1 ms作为算例，中心差分法与Newmark?β法运用CPU与GPU求解的试验子结构加速度时程对比如图4所示，GPU与CPU求解结果相同，说明GPU可以替代CPU作为实时混合试验的数值求解硬件。

在求解算法中使用Python中的time函数统计分别使用GPU与CPU，求解算法为中心差分法与Newmark?β法的计算耗时，结果如表2所示。表中SR（Speedup Ratio）为加速比，计算公式为SR=TCPU/TGPU，其中，TCPU为使用CPU求解每一步长平均耗时，TGPU为使用GPU求解每一步长平均耗时。

将表2中的数据绘图如图5所示，图5中纵坐标为单次求解模型所需的耗时，横坐标为模型自由度数。随着模型自由度的提升，两种算法求解所需的时间均有增加，使用CPU求解5400自由度模型耗时超过了实时混合试验的实时性要求（最大时间步长20 ms），而此时使用GPU求解仅需不到1 ms。模型规模越大，GPU相比CPU的加速越明显，当模型自由度为24375时，GPU相比CPU的加速比可达50余倍。无论是使用CPU还是GPU，条件稳定的中心差分法求解所需的时间均小于无条件稳定的Newmark?β法。原因是中心差分法的计算量相比Newmark?β法小，因此求解耗时短。

3 试验验证

本文使用Python作为编程语言，应用CuPy库进行基于GPU求解的实时混合试验，设计了振动台实时混合试验系统，验证试验系统的可行性。数值子结构部分GPU求解数值模型后将子结构交界面动力响应发送至信号处理部分。在信号处理部分，配置好Simulink xPC软件硬件环境，通过UDP网络连接数值子结构与物理子结构部分。物理子结构采用振动台作为加载装置。本文试验目的在于验证基于Python?GPU求解的实时混合试验系统的性能及可行性，为避免物理子结构试件建模误差，试验中物理子结构在xPC实时系统中仿真求解。当振动台系统接收到数值子结构的界面响应后振动台空台运行，测量振动台台面位移及加速度，传输至xPC中进行物理子结构仿真。物理子结构仿真计算的动力响应通过信号处理部分传输至数值子结构部分，由此构成如图6所示的基于Python?GPU求解的实时混合试验系统，图中试验子结构仿真部分为求解动力平衡方程，M为试验子结构质量；C为试验子结构阻尼；K为试验子结构刚度；ü为加速度；u˙为速度；u为位移；üt为外荷载加速度激励。试验中所用振动台照片如图7所示。

3.1 试验参数

试验中所用模型为本文2.2节土?结相互作用模型的缩尺模型，采用Wang等［24］提出的缩尺方法，缩尺比为104。数值子结构部分由ABAQUS有限元软件前处理得到，通过添加脚本提取模型参数并使用MATLAB将参数转换为矩阵形式。试验子结构部分为单自由度结构，采用Newmark?β算法仿真，质量ms=1.45 kg，刚度ks=1003 N/m，阻尼cs=0.374 N/（m?s?1）。试验在振动台台面布置位移及加速度传感器，对振动台输入白噪声信号并进行振动台系统辨识，使用3阶传递函数辨识振动台特性，振动台传递函数如下式所示：

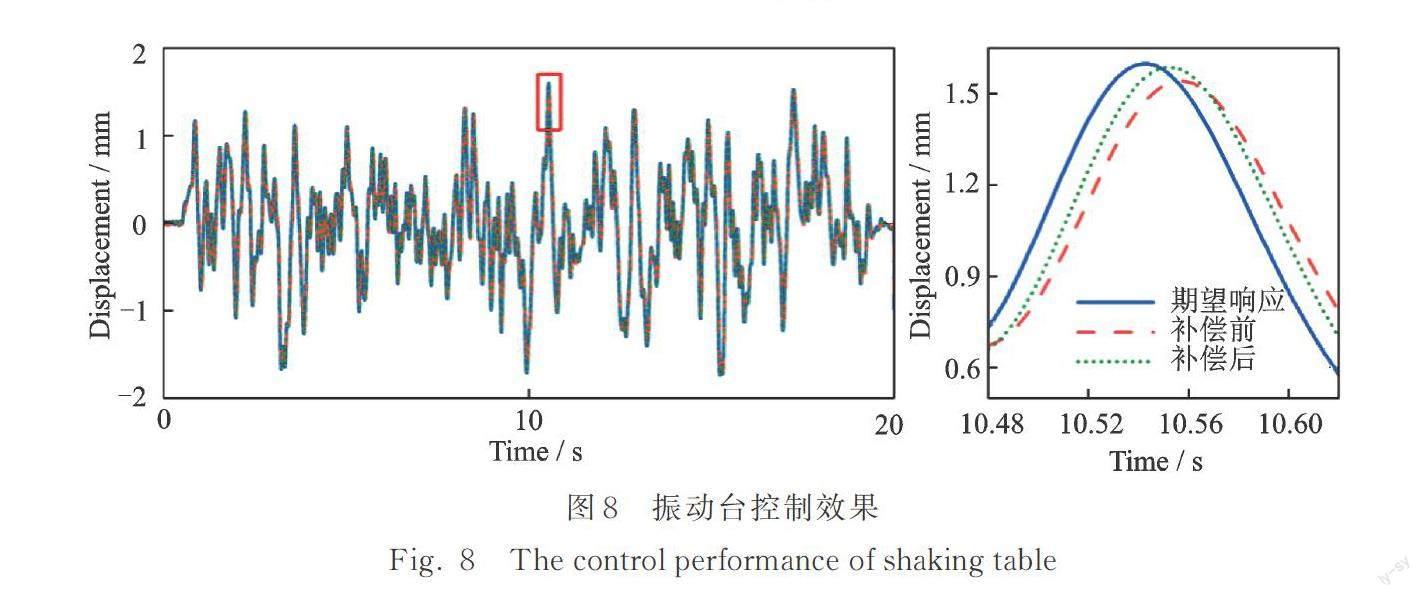
对振动台输入白噪声位移信号，振动台实际加载情况与期望的响应有幅值和相位误差。为此，在振动台信号输入前添加Tang等［25］提出的FSCS补偿控制器，对振动台系统进行控制补偿。补偿前后振动台位移时程对比如图8所示，补偿后的振动台幅值和相位误差相比未补偿时减小。

3.2 试验结果

实时混合试验中数值子结构模型自由度和求解时间步长对试验精度有影响，本文试验中分别选择使用GPU与CPU作为求解硬件，采用不同的时间步长、模型自由度对数值模型GPU求解性能进行对比。表3中工况1～8为时间步长为1 ms，5 ms，10 ms及20 ms时分别使用GPU与CPU求解数值子结构模型的最大自由度数；工况9与工况7对比求解相同自由度的子结构时，分别使用GPU与CPU可使用的最小时间步长。

对土?结相互作用模型进行整体仿真，使用时间步长为1 ms，GPU求解2592自由度模型实时混合试验与整体仿真试验子结构位移时程对比如图9所示。图9中混合试验与整体仿真结果吻合，说明基于Python?GPU的实时混合试验系统能满足试验精度的需要。图10为时间步长为1 ms，5 ms，10 ms以及20 ms分别使用GPU与CPU求解条件下，实时混合试验与整体仿真的试验子结构位移时程对比，8组工况条件试验与仿真结果一致，说明此试验系统精度较好，除求解硬件外其他试验条件相同时，使用GPU求解可以实现更大规模的实时混合试验。

在实时混合试验中，数值子结构求解采用数值积分算法，数值积分算法求解的精度与计算步长有关，求解算法的精度随着时间步长的增大而下降，过大的积分步长会导致条件稳定的数值积分算法计算发散。因此，算法的时间步长不能无限增大，在实时混合试验中时间步长最大取20 ms。为测试增大时间步长对试验精度的影响，试验中选择相同自由度数值子结构模型，不同时间步长进行测试。本试验中使用表1配置的CPU求解3549自由度模型，需要时间步长为20 ms，使用GPU求解相同模型仅需1 ms。使用1 ms，20 ms时间步长进行实时混合试验，试验结果与1 ms整体模型仿真对比如图11所示。图11中时间步长1 ms基于GPU求解的试验结果与整体仿真一致，时间步长20 ms基于GPU求解的试验结果与整体仿真峰值误差为2.88%，能满足实时混合试验的精度要求。董晓辉等［17］对实时混合试验中不同步长对中心差分法精度的影响进行测试，20 ms时间步长试验结果相比1 ms时间步长整体仿真误差达到10.28%。时间步长对无条件稳定的Newmark?β算法精度的影响相比条件稳定的中心差分法小，使用Newmark?β算法与大时间步长（20 ms）求解大规模数值模型仍具有较高的精度。

3.3 试验结果分析

由图10（a）～（b）可见，当时间步长为1 ms时，使用CPU求解的实时混合试验数值子结构模型为1215自由度，使用GPU求解能达到5400自由度，使用GPU能较大幅度提升数值子结构实时求解规模。得益于UDP网络的高速、高质量通讯，使得数值子结构与试验子结构实时交互界面响应，尽可能降低因信号通讯造成的精度影响。相较于使用LabVIEW作为信号通讯软件并通过模拟信号通讯的实时混合试验方法［17］，此试验系统架构可实现更小的GPU实时求解时间步长，优化试验系统架构，使得大规模数值模型实时求解实时混合试验成为可能，更小的时间步长可以提升试验精度。

由图10（g）～（h）可见，当时间步长为20 ms时，使用CPU求解的实时混合试验数值子结构模型为3549自由度，使用GPU求解时为24375自由度。此时GPU的求解性能相比CPU有了显著的提升，实现了CPU无法实时求解的大规模模型实时混合试验。使用LabVIEW?MATLAB的试验架构实现基于条件稳定的中心差分法20 ms时间步长24000自由度的实时混合试验，由于算法的条件稳定性，对数值模型具有一定限制［17］。本试验采用无条件稳定的Newmark?β算法，对模型参数无条件限制，相比条件稳定的算法进行实时混合试验拓展了应用范围。

分别使用1 ms和20 ms的时间步长，Newmark?β算法求解3549自由度数值子结构模型，记录其试验子结构位移时程结果。将1 ms和20 ms时间步长的混合试验结果与1 ms时间步长的整体仿真结果对比如图11所示。20 ms时间步长条件下使用无条件稳定的Newmark?β算法具有良好的精度，时间步长对Newmark?β算法的影响较小。因此，在基于GPU求解的实时混合试验中可以使用较大的时间步长（20 ms），实时求解更大规模的数值子结构模型。

4 结 论

本文使用Python作为编程语言，使用GPU建立了实时混合试验系统，通过仿真与试验验证了GPU求解数值子结构模型的性能，仿真与试验结果如下：

（1）相同时间步长下，使用Python?GPU相比于传统CPU可以实时求解更大规模的数值子结构模型。使用本文选择的GPU和CPU作为求解硬件，无条件稳定的Newmark?β算法在20 ms时间步长条件下，可实现24375自由度模型的实时混合试验。

（2）相同数值子结构自由度条件下，使用Python?GPU相比于CPU可以实现更小积分步长的实时混合试验。使用本文选择的GPU和CPU作为求解硬件，数值积分算法为无条件稳定的Newmark?β算法时，CPU求解3549自由度模型时需要时间步长为20 ms，而GPU求解仅需1 ms的时间步长，更小积分步长有利于提高实时混合试验精度。

（3）Python?GPU相比于LabVIEW?MATLAB的GPU试验架构，提升了子结构之间的数据通讯效率，使得基于GPU求解的实时混合试验最小步长由4 ms降低至1 ms，并且实现了无条件稳定Newmark?β算法的GPU加速，避免了算法稳定性对模型的限制。时间步长增加对Newmark?β算法的影响相比中心差分法小，Newmark?β算法求解大规模数值模型时使用大时间步长仍有较高精度，进一步拓展了实时混合试验的应用范围。本文选择的阻尼模型为Rayleigh阻尼，数值积分算法为中心差分法与Newmark?β算法，若采用更高效的阻尼模型和数值求解算法，与GPU并行计算相结合有望进一步提升模型实时求解的效率。

参考文献

1Nakashima M， Kato H， Takaoka E. Development of real‐time pseudo dynamic testing［J］. Earthquake Engineering & Structural Dynamics， 1992， 21（1）： 79-92.

2孟凡涛， 赵建锋， 于广明. 实时子结构混合试验中的数值积分方法对比分析［J］. 地震工程与工程振动， 2011， 31（5）： 60-67.

Meng Fantao， Zhao Jianfeng， Yu Guangming. Study on numerical integration methods in real-time hybrid testing experiment［J］. Earthquake Engineering and Engineer Dynamics， 2011， 31（5）： 60-67.

3王倩穎， 吴斌， 欧进萍. 考虑作动器时滞及其补偿的实时子结构实验稳定性分析［J］. 工程力学， 2007， 24（2）： 9-14.

Wang Qianying， Wu Bin， Ou Jinping. Stability analysis of real-time substructure testing considering actuator delay and compensation［J］. Engineering Mechanics， 2007， 24（2）： 9-14.

4洪越， 唐贞云， 何涛， 等. 大尺寸非线性实时动力子结构试验实现［J］. 振动工程学报， 2017， 30（6）： 913-920.

Hong Yue， Tang Zhenyun， He Tao， et al. The implementation of nonlinear real-time dynamics substructuring for large scale specimen［J］. Journal of Vibration Engineering， 2017， 30（6）：913-920.

5Nakashima M， Ishida M， Ando K. Integration techniques for substructure pseudo dynamic test： pseudo dynamic test using substructuring techniques［J］. Journal of Structural and Construction Engineering（Transactions of AIJ）， 1990， 417： 107-117.

6Chang S Y. Explicit pseudodynamic algorithm with unconditional stability［J］. Journal of Engineering Mechanics， 2002， 128（9）： 935-947.

7Chang S Y. A new family of explicit methods for linear structural dynamics［J］. Computers & Structures， 2010， 88（11-12）： 755-772.

8吴斌， 保海娥. 实时子结构实验Chang算法的稳定性和精度［J］. 地震工程与工程振动， 2006， 26（2）： 41-48.

Wu Bin， Bao Haie. Stability and accuracy of Chang algorithm for real-time substructure testing［J］. Earthquake Engineering and Engineering Vibration， 2006， 26（2）： 41-48.

9Chen C， Ricles J M. Development of direct integration algorithms for structural dynamics using discrete control theory［J］. Journal of Engineering Mechanics， 2008， 134（8）： 676-683.

10Tang Y， Lou M L. New unconditionally stable explicit integration algorithm for real-time hybrid testing［J］. Journal of Engineering Mechanics， 2017， 143（7）：04017029.

11Nakashima M， Masaoka N. Real-time on-line test for MDOF systems［J］. Earthquake Engineering & Structural Dynamics， 1999， 28（4）： 393-420.

12Chae Y， Kazemibidokhti K， Ricles J M. Adaptive time series compensator for delay compensation of servo‐hydraulic actuator systems for real‐time hybrid simulation［J］. Earthquake Engineering & Structural Dynamics， 2013， 42（11）： 1697-1715.

13Zhu F， Wang J T， Jin F， et al. Simulation of large-scale numerical substructure in real-time dynamic hybrid testing［J］. Earthquake Engineering and Engineering Dynamics， 2014， 13（4）： 599-609.

14Lu L Q， Wang J T， Zhu F. Improvement of real-time hybrid simulation using parallel finite-element program［J］. Journal of Earthquake Engineering， 2020， 24（10）： 1547-1565.

15劉晓强. 面向土木工程数值模拟的可视化方法研究［D］. 北京： 清华大学， 2013.

Liu Xiaoqiang. Research on visualization method for civil engineering numerical simulation［D］. Beijing： Tsinghua University， 2013.

16解琳琳， 韩博， 许镇， 等. 基于OpenSees的大型结构分析GPU高性能计算方法［J］. 土木建筑工程信息技术， 2014， 6（5）： 22-25.

XIE Linlin， HAN Bo， XU Zhen， et al. GPU powered high-performance computing method for the analysis of large-scale structures based on OpenSees［J］. Journal of Information Technology in Civil Engineering and Architecture， 2014， 6（5）： 22-25.

17董晓辉， 唐贞云， 李振宝， 等. 应用GPU求解的实时子结构试验架构与性能验证［J］. 振动工程学报，2022，35（1）：64-71.

Dong Xiaohui， Tang Zhenyun， Li Zhenbao， et al. Performance verification of GPU-based framework for real-time hybrid testing［J］. Journal of Vibration Engineering，2022，35（1）：64-71.

18Okuta R， Unno Y， Nishino R， et al. CuPy： a NumPy-compatible library for NVIDIA GPU calculations［C］. 31st Confernce on Neural Information Processing Systems （NIPS 2017）. Long Beach， CA， 2017.

19Goerzen J，Bower T， Rhodes B. Foundations of Python Network Programming［M］. Berkeley： Apress， 2010.

20李彬. 基于Windows的计算机数字控制系统实时性的研究［D］. 哈尔滨： 哈尔滨工业大学， 2008.

Li Bin. Research on real-time performance of computer numerical control system based on Windows［D］. Harbin： Harbin Institute of Technology， 2008.

21Rosenquist C. Hard realtime rapid prototyping development platform［D］. Link?ping： Link?ping University， 2003.

22进兵. 基于xPC Target的无人机飞行控制软件快速原型设计［D］. 南京： 南京航空航天大学， 2008.

Jin Bing. Rapid prototype design for flight control software of UAV based on xPC Target［D］. Nanjing： Nanjing University of Aeronautics and Astronautics， 2008.

23Tang Z Y， Dietz M， Hong Y， et al. Performance extension of shaking table-based real-time dynamic hybrid testing through full state control via simulation［J］. Structural Control & Health Monitoring， 2020， 27（10）： e2611.

24Wang Qiang， Wang Jinting， Jin Feng， et al. Real-time dynamic hybrid testing for soil-structure interaction analysis［J］. Soil Dynamics and Earthquake Engineering， 2011， 31（12）： 1690-1702.

25Tang Z Y， Dietz M， Li Z B， et al. The performance of delay compensation in real-time dynamic substructuring［J］. Journal of Vibration and Control， 2018， 24（21）： 5019-5029.

Research on real-time hybrid simulation by Python-GPU computing

DONG Xiao-hui 1 ?TANG Zhen-yun 1，2 ?LI Zhen-bao 1DU Xiu-li 1

1. The Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education， Beijing University of Technology， Beijing 100124， China；

2. Hebei Key Laboratory of Earthquake Disaster Prevention and Risk Assessment， Sanhe 065201， China

Abstract This article establishes an RTHS framework based on Python and graphics processor unit （GPU） computation. Using a soil-structure interaction system as a testing model， the performance of the testing framework is verified by numerical simulation and experiment. The results show that using Python-GPU to speed the unconditionally stable algorithm allows a numerical substructure with 24000 DOFs to be solved in a time step of 20 ms. Because the scale of GPU calculation is almost 7 times greater than that of CPU calculation in the same machine， the capability of RTHS is greatly extended.

Keywords real-time hybrid simulation; graphics processing unit; Python; numerical integration algorithm; calculation efficiency