利用改进交叉模型交叉模态的随机模型修正方法

王炎 陈辉 黄斌 柴满

摘要 将混合摄动?伽辽金方法和改进的交叉模型交叉模态技术相结合，提出了一种随机模型修正方法。该方法有效缓解了模型修正过程中测量数据有限和测量误差不确定的影响。考虑到实测模态数据具有不确定性，基于改进的交叉模型交叉模态方法，建立了一个新的描述结构随机参数和随机响应关系的模型修正方程。利用混合摄动?伽辽金方法求解该随机修正方程，进而得到结构随机修正参数的统计特征。简支梁的数值结果表明，该方法在测量数据不确定性较大时仍能保持很高的修正精度，同时计算效率比蒙特卡罗模拟方法高出一个数量级。在测量模态数据较少的情况下，该方法比单独的混合摄动?伽辽金修正方法修正效果好，且比交叉模型交叉模态法的修正精度更高。框架试验的结果表明，该方法可以同时修正结构的刚度和质量，修正后的结构参数与预设工况基本吻合，同时能复现结构的测量模态，从而验证了所提方法的有效性。

关键词 随机模型修正; 随机混合?摄动伽辽金方法; 改进的交叉模型交叉模态方法

引 言

近几十年来，基于动力测量数据的有限元模型修正方法越来越受到关注。许多研究人员在这一领域进行了广泛的研究，并取得了大量研究成果［1?4］。

在动力有限元模型修正中，修正参数的选择对修正结果有很大影响。如果修正参数过多，在修正过程中往往会出现病态问题，所以在修正模型之前首先要排除不敏感的修正参数［5］。关于动力有限元模型修正方法，Hu等［6］提出了一种基于交叉模型交叉模态（CMCM）方法的模型修正技术。与传统的模型修正方法不同，该方法可以同时修正结构的刚度矩阵、质量矩阵和阻尼矩阵。此外，该方法不用迭代计算，计算效率较高。在CMCM方法中，通过将结构的实测模态和计算模态相乘，就可以仅用少量的测量模态构建多个模型修正方程。李世龙等［7］利用CMCM方法，提出了一种有效识别子结构边界约束状态的模型修正方法。Wang等［8］使用了CMCM方法对海上平台进行了试验研究，证明了当结构的实际测量模态不完整且只有低阶测量模态可用时CMCM方法的有效性。在已有的CMCM方法的基础上，Liu等［9］提出了一种基于改进的交叉模型交叉模态（ICMCM）的模型修正方法，该方法充分利用实测数据，进一步增加了修正方程的个数。然而，这些方法仅涉及确定性有限元模型修正，當结构参数的不确定性或者测量噪声无法避免时，现有的CMCM方法将不适用。因此，充分利用CMCM方法的优点，并将它融入随机模型修正中，是一项非常有意义的工作。

在随机模型修正领域中，蒙特卡罗方法、摄动法以及贝叶斯方法被广泛使用。Schu?ller等［10］使用了具有大样本的蒙特卡罗模拟来计算模型修正的统计特性。宗周红等［11］在对下白石连续刚构桥进行模型修正的过程中，利用蒙特卡罗模拟方法和有限元方法进行不确定性量化分析，并评价模型的预测精度，实现对于连续刚构桥的有限元模型确认。但是对于大型结构而言，这种方法的计算效率太低，耗时过长。与蒙特卡罗方法不同的是，摄动法具有推导简单、计算效率高的特点。Hua等［12］使用一种改进的摄动法，利用随机实测模态数据对桁架桥有限元模型进行修正，并估计了结构参数的均值和均方差。尽管摄动法的计算效率比较高，但其对测量误差的变异性要求比较苛刻。随机模型修正方法中，另一个具有代表性的方法是基于马尔可夫链与蒙特卡罗抽样的贝叶斯方法［13?15］，但是基于此种抽样的贝叶斯方法会面临较大的挑战，即需要非常耗时的重复有限元计算。为了提高计算效率，Wan等［16］和Fang等［17］分别采用了高斯代理模型和随机响应面模型对原有的贝叶斯方法进行了改进。与上述方法不同，Huang等［18］提出了一种基于混合摄动?伽辽金方法（HPG）的随机模型修正方法（HPG?SMUM），该方法在测量变异性较大情况下具有比较高的修正精度和效率，此方法也为确定性模型修正方法扩展到随机领域提出了一个新的思路和完整的框架。

本文将随机摄动?伽辽金方法与改进的交叉模型交叉模态方法结合，提出一种随机模型修正方法。该方法可利用含测量误差的少量模态测量数据实现结构有限元模型的有效修正。文中用一个简支梁的数值算例来验证该方法的有效性和不同模态组合的稳定性，并利用七层框架的模态试验来验证所提方法在较少测量模态情况下仍能同时有效地修正结构刚度和质量。

1 基于ICMCM的随机模型修正方程

考虑具有N个自由度的无阻尼结构，该结构初始模型满足以下特征值方程：

式中 Ka和Ma分别为初始结构模型的整体刚度矩阵和质量矩阵；λi和?i分别为初始模型的第i阶特征值和特征向量；nc为初始模型的计算模态的个数。

类似地，实际结构的特征值方程可以表示为：

式中 Kd和Md分别为实际结构模型的整体刚度矩阵和质量矩阵；λ?j和??j分别为实际模型的第j阶特征值和特征向量；nm为实际模型的计算模态的个数。

初始结构与实际结构的质量矩阵、刚度矩阵存在以下关系：

式中 Ne为结构的单元个数；Kn和Mn分别为结构第n个单元的N×N单元组装矩阵；αn和βn分别为结构第n个单元的刚度和质量的修正系数，表示实际结构的单元刚度和质量相对于初始矩阵的变化率。

通过文献［6］可以得到确定性的基于交叉模型交叉模态的模型修正方程为：

对式（5）进行因式变换可以得到：

通过求解式（6）所示的方程组可以得到刚度和质量的修正系数αn和βn。但是由于在实际的模态测量中只能精确测量出前几阶模态，使得修正系数方程组的方程个数比较少，导致求解结果不正确且不稳定。因此Liu等［9］对传统的CMCM方法进行改进，充分利用测量模态数据，在式（2）方程两边同时乘??Tj，得到如下所示的基于ICMCM的模型修正方程：

对式（7）进行因式变换，可以得到：

显然，式（8）也含有与方程（6）相同的修正系数，结合式（6）和（8），就可以得到更多的修正方程，确保修正方程的适定性。

在实际结构的模态试验过程中，不可避免地会遇到测量误差。假定第j阶的特征值和特征向量可以表示为：

式中 λ?0j和??0j分别为测量的第j阶特征值和特征向量均值；λ?1j和??1j分别为第j阶测量误差的确定性部分；ξj为与测量误差相关的随机变量，且随机变量的分布类型由实测数据的统计特征或者是工程经验决定。

假设所有随机变量ξj完全相关，并且表示为随机变量ξ，则第n个刚度单元和质量单元的修正系数可以分别用下式表示：

上述方法就是本文所提出的结合HPG和ICMCM的随机模型修正方法（HPG?ICMCM）。假设用[C（0）E（0）]和[C（1）E（1）]代替式（19），（22）和（25）中的[C（0）IE（0）I]和[C（1）IE（1）I]，相应的向量γ（0），γ（1），γ（2）也可以通过上述方式递推得到。此时，HPG?ICMCM方法退化为HPG?CMCM方法。

需要注意的是，实际结构的转角模态往往难以测量。此外，由于测量条件的限制，仅能测量包括部分测点的振型。因此，本文使用文献［19］的模态扩阶方法得到完备振型的均值和标准差。同时，在求解方程组（19），（22）和（25）的过程中，采用截断奇异值分解或者L1正则化技术［20］避免方程病态的问题。

3 数值算例

考虑一个简支梁，如图2所示。简支梁的跨度为6 m，截面为0.2 m×0.25 m，弹性模量为2.8×1010 Pa，密度为2.5×103 kg/m3。将该Euler?Bernoulli梁的有限元模型沿梁长度方向划分为15个相同的单元，每个节点包含竖向位移和转角两个自由度。

根据测量经验，可以假设实测模态数据服从某种概率分布，如正态分布或者β分布。由于实测数据是有界的，本文假设实测模态数据服从β分布。依据工程经验，动力特性测试数据的变异系数一般在0.01～0.02之间，这里假设变异系数为0.02。

首先，考虑结构质量不发生变化，单元1，3，7，9和11的刚度分别减小30%，15%，20%，20%和30%，其余单元的刚度和初始模型相同。取前六阶初始模型的计算模态和前六阶测量模态，使用HPG?ICMCM方法和HPG?CMCM方法对模型进行修正，同時利用与本文所提出的方法对应的蒙特卡罗模拟方法（MC?ICMCM）和Huang等［18］的HPG?SMUM方法求解上述方法中的修正系数的统计特性，在求解过程中使用奇异值分解正则化技术降低矩阵求逆的不适定性，以提高计算精度。修正结果如图3和4所示。

观察图3和4，不难看出，当结构的自由度比较多但测量模态有限时，通过HPG?SMUM方法得到的修正系数均值和预设的真实值差别比较大。例如，HPG?SMUM方法得到的单元1刚度修正系数均值为-0.02，和MC?ICMCM方法结果相比，相对误差接近90%。同时，单元2，15的刚度修正系数均小于-0.1，出现了明显误判。对于单元8，10，13和15，HPG?SMUM方法的修正系数标准差结果和MC?ICMCM方法结果最大相对误差达到400%，说明在这种情况下HPG?SMUM方法修正效果不能令人满意。而通过HPG?ICMCM方法和HPG?CMCM方法得到的各单元修正系数与MC?ICMCM相比较，均值的绝对误差均未超过0.03，标准差的相对误差基本小于20%。可以说明统计结果和仿真试验预设的结果基本吻合，并且HPG?ICMCM方法的均值结果吻合更好。

为了验证同时修正质量和刚度时本文方法的有效性，假设单元3，5，6，8，9，11和13的实际质量分别增加10%，20%，20%，20%，20%，20%和10%，同时，单元1，3，5，7，9，11和13的弹性模量分别降低30%，15%，20%，20%，20%，30%和30%，其余单元的质量和刚度和初始模型相同。选择这15个单元的质量和弹性模量作为待修正的参数。首先假设测量得到了被测结构的前六阶模态的频率和竖向位移振型，再通过模态扩阶方法得到被测模态的完整形式。之后对于初始模型，通过计算得到其前七阶模态数据。这里分别使用MC?ICMCM，HPG?ICMCM和HPG?CMCM三种方法进行模型修正。修正系数的统计特性如图5～8所示。

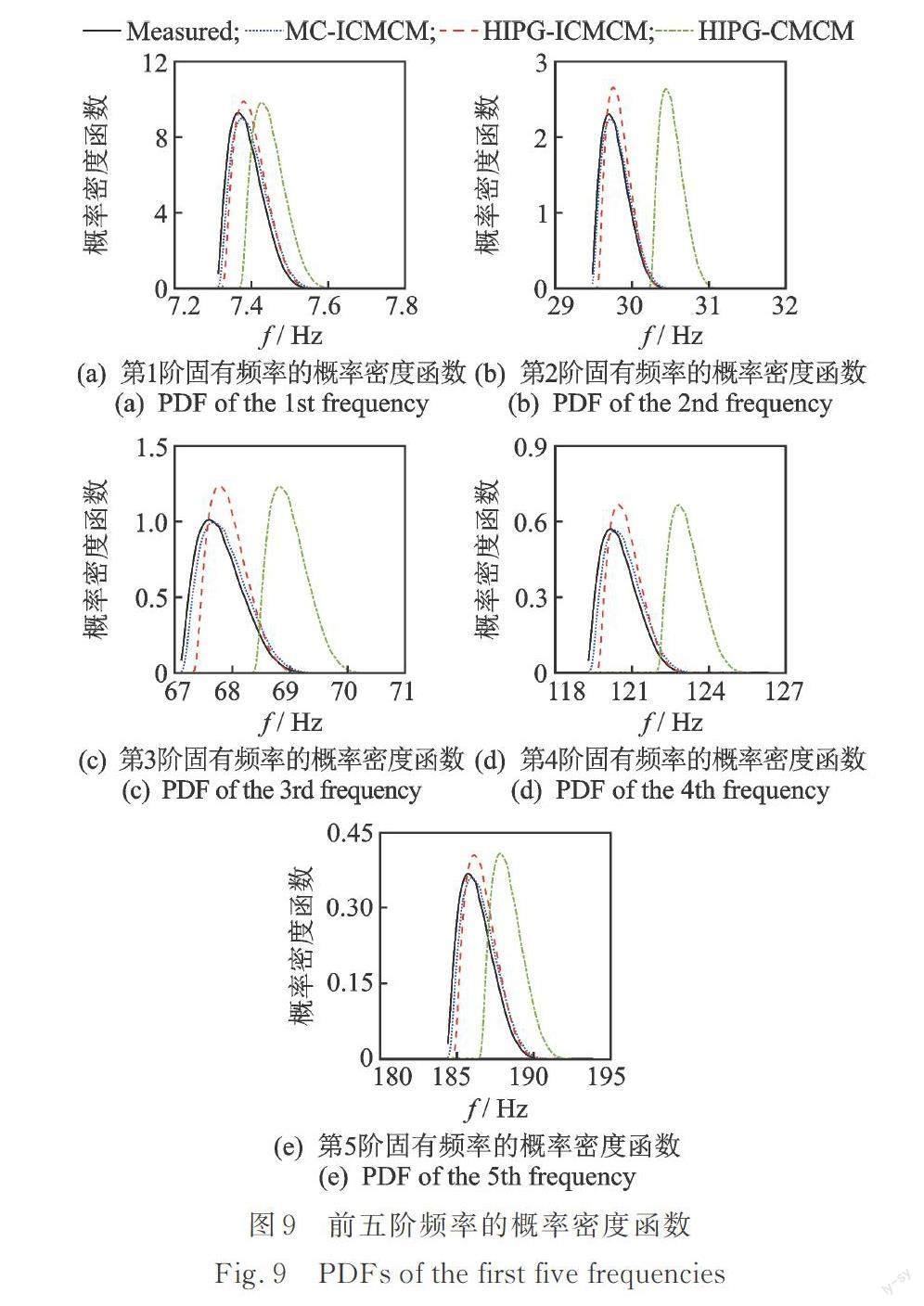
从图5～8中可以看出，一方面，在刚度和质量出现变化的单元里，由HPG?ICMCM方法得到的刚度和质量修正系数均值与MC?ICMCM方法得到结果的相对误差均小于10%。并且，除了单元3之外，各单元刚度与质量修正系数标准差与MC?ICMCM方法相比均小于30%，这个现象说明所提出的HPG?ICMCM方法的修正精度和效果是令人满意的。另一方面，HPG?CMCM方法的修正系数均值和预设的值相差较大，特别是在修正刚度时，除单元11和13以外，均出现了明显的误判。从而可以说明HPG?ICMCM方法得到的修正系数的统计特性比HPG?CMCM方法更加接近假定的真值，并且与MC?ICMCM方法得到的结果非常接近。除此之外，为了分析测量误差变异系数对HPG?ICMCM方法和HPG?CMCM方法的影响，图9给出了变异系数为0.02时，修正后结构的前五阶频率的概率密度函数。

从图9中可以看出，HPG?ICMCM方法与蒙特卡罗模拟方法的结果吻合，而通过HPG?CMCM方法得到的修正频率不符合仿真预设的实测频率。这进一步说明了HPG?ICMCM方法的优越性。此外，基于三万个样本的MC?ICMCM方法在CPU为i5?10400、运行内存16 GB的个人计算机上计算时间超过了1800 s，而本文提出的HPG?ICMCM方法仅用时120 s，二者对比说明了此方法的高效率。

对于不同的模态组合，文献［9］指出当测量模态数据较少时，确定性CMCM方法可能会导致修正结果不稳定。接下来，将验证在有限实测数据的情况下，HPG?ICMCM方法的稳定性。假设质量和刚度的折减量与之前简支梁仿真算例的预设值完全相同，不进行模态扩阶，考虑计算和测量模态的不同组合工况。不同工况下，模态组合如表1所示。

在这四种工况下，采用HPG?ICMCM方法对简支梁进行模型修正，得到单元修正系数的统计特性，如图10～13所示。图10～13结果显示在四种不同的模态组合中，获得的修正系数统计特性非常接近。

从图14中可以看到，选取不同的模态组合都可以得到较准确的修正结果。由于采用了ICMCM方法增加了修正方程数量，尽管测量模态的数量逐渐减少，修正后的频率仍然能很好地与测量结果吻合，说明了本文提出方法的稳定性。

4 七层框架试验

为了验证HPG?ICMCM方法的有效性，制作了一个七层框架，如图15（a）所示。该七层框架层高为150 mm，框架动力模型采用葫芦串模型，如图15（b）所示，各单元质量为每层铝合金质量块及低频传感器和夹具组成。层间刚度由两侧的钢板提供，两侧侧板均采用1 mm厚的304不锈钢板切割成型制作。框架的底部使用螺丝紧固在试验台上。层间钢板材料的弹性模量为194 GPa、密度为7.93 g/cm3，泊松比为0.3。每层侧板的宽度为100 mm，在框架的模态试验中，将第2，4和6层间两侧的钢板分别切除30%，10%和20%，用来模拟刚度退化。框架的各单元的质量如表2所示，在单元2，4和5处附加质量块模拟质量变化。在模态测试中，使用5个加速度传感器分两批测量。由于传感器的重量不能忽略，为了使测试过程中每层质量相同，因此在没有布置传感器的层中布置与传感器等重的配重块。试验中，采取了6种不同的传感器布置方式进行了6组测量。

每一组测量均采用不测力法对框架结构进行模态测试。在采集了7个测量点的加速度数据之后，使用增强型频域分解方法［21］识别该框架的模态，并采用测量软件内5种不同的分析点数（512，1024，2048，4096，8192）进行模态分析。对30组样本进行统计分析之后，得到前三阶测量模态的均值，并且得出测量频率的变异系数为0.01。预计在实际工程测量中变异系数会更大。

选择前三阶实测模态和初始模型的前四阶计算模态用于模型修正，将7个单元的弹性模量和质量作为修正系数，总共14个修正参数。其中，七层框架的刚度修正系数从下到上编号为1～7，每层对应的质量修正系数编号为8～14。采用HPG?ICMCM方法进行计算，并使用L1正则化技术降低求解过程中矩阵求解的不适定性，得到修正系数的统计特性如图16和17所示。

从图16中可以看出，修正参数的均值与预设工况基本吻合。由于测量误差的随机性，修正后的参数也具有随机性，修正系数的标准差如图17所示。从图17中可以看出，修正系数的标准差最大值为0.03，最小值为0.005。用修正后的参数计算结构频率的概率密度函数，如图18所示。从图18中可以看出，本文方法修正的结构频率概率密度与测量结果基本一致。这说明了本文方法对于试验框架结构是有效的。

5 结 论

本文提出了一种交叉模型交叉模态随机有限元模型修正方法。该方法成功地将确定性的改进交叉模型交叉模态模型修正方法拓展到随机领域。建立了基于ICMCM方法的随机模型修正方程，并对方程进行了求解。该方法同时具备了ICMCM方法仅用少量模态即可构造大量修正方程的优点，以及能够考虑测量误差的随机性，并能用混合摄动?伽辽金方法高效求解隨机模型修正方程的优点。

简支梁算例的结果表明，本文方法可以有效处理测量数据中较大的不确定性，并且计算效率要比直接采用蒙特卡罗模拟方法高出1个数量级。当测量数据较少时，新的方法比已有的混合摄动?伽辽金修正方法修正效果好，且比交叉模型交叉模态法的修正精度更高。七层框架结构试验表明了本文方法对实际结构模型修正的有效性。

参考文献

1Mottershead J E， Friswell M I. Model updating in structural dynamics： a survey［J］. Journal of Sound & Vibration， 1993， 167（2）： 347-375.

2李辉， 丁桦. 结构动力模型修正方法研究进展［J］. 力学进展， 2005， 35（2）： 170-180.

LI Hui， DING Hua. Progress in model updating for structural dynamics［J］. Advances in Mechanics， 2005， 35（2）： 170-180.

3姜东， 费庆国， 吴邵庆. 基于区间分析的不确定性结构动力学模型修正方法［J］. 振动工程学报， 2015， 28（3）： 352-358.

JIANG Dong， FEI Qingguo， WU Shaoqing. Updating of structural dynamics model with uncertainty based on interval analysis［J］. Journal of Vibration Engineering， 2015， 28（3）： 352-358.

4Wan H P， Ren W X. A residual-based Gaussian process model framework for finite element model updating［J］. Computers and Structures， 2015， 156： 149-159.

5Wan H P， Ren W X. Parameter selection in finite element model updating by global sensitivity analysis using Gaussian process metamodel［J］. Journal of Structural Engineering， 2015， 141（6）： 04014164.

6Hu S L J， Li Huajun， Wang Shuqing. Cross-model cross-mode method for model updating［J］. Mechanical Systems & Signal Processing， 2007， 21（4）： 1690-1703.

7李世龙， 马立元， 李永军， 等.一种新的子结构边界约束模型修正方法及其应用［J］. 振动工程学报， 2015， 28（5）： 730-740.

LI Shilong， MA Liyuan， LI Yongjun， et al. A method for model updating of substructure boundary constraints and its application［J］. Journal of Vibration Engineering， 2015， 28（5）： 730-740.

8Wang Shuqing， Li Yingchao， Li Huajun. Structural model updating of an offshore platform using the cross model cross mode method： an experimental study［J］. Ocean Engineering， 2015， 97： 57-64.

9Liu K， Yan R J， Guedes Soares C. An improved model updating technique based on modal data［J］. Ocean Engineering， 2018， 154： 277-287.

10Schu?ller G I， Calvi A， Pellissetti M F， et al. Uncertainty analysis of a large-scale satellite finite element model［J］. Journal of Spacecraft and Rockets， 2009， 46（1）： 191-202.

11宗周紅， 高铭霖， 夏樟华. 基于健康监测的连续刚构桥有限元模型确认（Ⅱ）——不确定性分析与模型精度评价［J］. 土木工程学报， 2011， 44（3）： 85-92.

ZONG Zhouhong， GAO Minglin， XIA Zhanghua. Finite element model validation of the continuous rigid frame bridge based on structural health monitoring—part Ⅱ： uncertainty analysis and evaluation of model accuracy［J］. China Civil Engineering Journal， 2011， 44（3）： 85-92.

12Hua X G， Ni Y Q， Chen Z Q， et al. An improved perturbation method for stochastic finite element model updating［J］. International Journal for Numerical Methods in Engineering， 2008， 73（13）： 1845-1864.

13Beck J L， Katafygiotis L S. Updating models and their uncertainties. I： Bayesian statistical framework［J］. Journal of Engineering Mechanics， 1998， 124（4）： 455-461.

14Katafygiotis L S， Beck J L. Updating models and their uncertainties. II： model identifiability［J］. Journal of Engineering Mechanics， 1998， 124（4）： 463-467.

15Lam H F， Yang J H， Au S K. Markov chain Monte Carlo-based Bayesian method for structural model updating and damage detection［J］. Structural Control and Health Monitoring， 2018， 25（4）： e2140.

16Wan H P， Ren W X. Stochastic model updating utilizing Bayesian approach and Gaussian process model［J］. Mechanical Systems and Signal Processing， 2016，70-71： 245-268.

17Fang S E， Chen S， Lin Y Q， et al. Probabilistic damage identification incorporating approximate Bayesian computation with stochastic response surface［J］. Mechanical Systems and Signal Process， 2019， 128： 229-243.

18Huang B， Chen H. A new approach for stochastic model updating using the hybrid perturbation-Galerkin method［J］. Mechanical Systems and Signal Process， 2019， 129： 1-19.

19張德文. 改进Guyan～递推减缩技术［J］. 计算结构力学及其应用， 1996， 13（1）： 90-94.

ZHANG Dewen. An improved Guyan reduction and successive reduction procedure of dynamic model［J］. Chinese Journal of Computational Mechanics， 1996， 13（1）： 90-94.

20Zhou X Q， Xia Y， Weng S. L1 regularization approach to structural damage detection using frequency data［J］. Structural Health Monitoring， 2015， 14（6）： 571-582.

21Brincker R， Zhang L， Andersen P. Modal identification from ambient responses using frequency domain decomposition［A］. Proceedings of IMAC?ⅩⅧ： A Conference on Structural Dynamics［C］. USA： Society for Experimental Mechanics， 2000： 625-630.

Stochastic model updating method using the improved cross-model cross-mode technique

WANG Yan 1 ?CHEN Hui 1，2HUANG Bin 1 ?CHAI Man 1

1. School of Civil Engineering and Architecture， Wuhan University of Technology， Wuhan 430070， China；

2. College of Post and Telecommunication， Wuhan Institute of Technology， Wuhan 430073， China

Abstract In this paper， a new stochastic model updating method is proposed， which combines the random hybrid perturbation-Galerkin method with the improved cross-model cross-mode technique. This method effectively alleviates the impaction of limited measurement data and uncertain measurement errors on model updating. Considering the uncertainty of the measured modal data， a new stochastic updating equation with update coefficient vector is established based on the improved cross-model cross-mode method. Using the hybrid perturbation-Galerkin method to solve the stochastic updated equation， the update coefficient vector is obtained. The statistical characteristics of the update coefficients can then be determined. The numerical results of the simply supported beam show that the proposed method can effectively deal with the relatively large uncertainty in the actual measurement data， and shows relatively strong stability in the case of different modal combinations， and has a higher computational efficiency than the Monte Carlo method. Considering the rank deficit， the improved cross-model cross-mode method proposed in this paper can get better updating results than the cross-model cross-mode method. The experimental results of the frame show that the new method can simultaneously modify the stiffness and the quality of the structure， and the updated model can be used to obtain modal data consistent with the measured results， thus verifying the effectiveness of the proposed method.

Keywords stochastic model updating; hybrid perturbation-Galerkin method; improved cross-model cross-mode technique