考虑轴承刚度软化的转管炮身管组固有频率分析
2023-07-05钱麒合林圣业戴劲松王茂森宁春交
钱麒合,林圣业,戴劲松,王茂森,宁春交
(1.南京理工大学 机械工程学院,江苏 南京 290014;2.长安工业有限责任公司,重庆 400023)
转管炮具有射速高、威力大、可靠性好等优点,广泛装备于陆、海、空各军种。转管炮射击时,由若干炮管集束而成的身管组在滚动轴承支撑下高速旋转,身管组与滚动轴承构成组合转子-轴承系统。已有研究表明[1-2],滚动轴承在高速旋转条件下会出现刚度软化现象,即当转速低于某一极限值时,滚动轴承刚度基本保持不变,而当转速超过该极限值后,滚动轴承刚度将随转速增大而急剧降低。从动力学角度看,轴承刚度特性直接影响转子系统固有频率,进而影响全炮射击精度和发射安全性。随着转管炮不断朝着高射速方向发展,滚动轴承刚度软化对转管炮身管组固有频率的影响日益突出。因此,在转管炮设计阶段,必须考虑轴承在高速条件下的刚度软化效应,准确计算转子系统固有频率,为身管组固有频率与射速的匹配性设计提供理论支撑。
目前,国内外学者开展了大量关于转管炮身管组固有频率特性的研究,分析方法主要包括有限元法[3-4]和传递矩阵法[5-7]。有限元法的优点是能够较全面地反映转管炮身管组的复杂结构特征,计算精度高,是目前转管炮身管组固有频率特性分析应用最广泛的方法。如杨凡[3]采用有限元方法,建立了舰炮身管、摇架等部件的有限元模型,根据振动理论,对舰炮系统进行模态分析,计算各部件约束条件下的固有频率和振型,分析各部件结构上可能的薄弱环节;黄晨烨等[4]利用有限元仿真对某新型火炮身管组进行分析,分别考虑单炮箍及双炮箍对身管组固有频率的影响。然而现有的转管炮有限元模型均是在静止假设条件下建立的,尚未考虑高速旋转引起的身管组离心效应、陀螺效应和滚动轴承刚度软化效应。因此,相关研究结论仅适用于转速较低的情况。随着转管炮射速不断提高,现有转管炮有限元分析模型的计算误差较大,已不能满足现代高射速转管炮设计的需求。
传递矩阵法的最大优势是传递矩阵的维度不随单元划分数的增加而变化,特别适用于像转管炮这样的链式系统。如芮筱亭等[5-7]结合多体系统传递矩阵法[8]和有限元传递矩阵法[9],建立了多体系统有限元传递矩阵法[10],解决了同时含有多个刚体和弹性体的复杂刚柔混合舰炮系统振动特性的计算问题,获得了舰炮的振动特性。屠天雄等[11]采用传递矩阵法建立了考虑身管组陀螺效应的转管炮身管组动力学模型,分析了转管炮身管组的固有频率特性,为转管炮结构设计提供了重要指导。上述研究虽然将滚动轴承简化为线性弹簧,考虑了支承刚度的影响,但仍未考虑滚动轴承刚度软化导致的刚度非线性效应。
针对现有转管炮动力学模型尚未考虑滚动轴承刚度软化效应,导致高速条件下身管组固有频率计算精度不足的问题,笔者采用有限元方法建立转管炮身管组转子-滚动轴承系统动力学模型,继而分析转管炮身管组固有频率特性,揭示滚动轴承刚度软化对转管炮身管组固有频率的影响规律,并研究了轴承间隙对轴承刚度和身管组固有频率的影响,为转管炮提高射击精度提供了理论依据。
1 理论模型
转管炮由身管组、星形体、滚动轴承和炮箱等部件组成,如图1所示。身管组采用单悬臂支承结构固定于星形体前部,滚动轴承安装于身管组第三支点处以及星形体上的滚道槽处,星形体通过滚动轴承安装于炮箱内。

1.1 基本假设
1)身管组上各零件的材料相同;
2)材料各向同性且质地均匀;
3)不考虑温度对材料性能的影响。
1.2 转管炮身管组有限元模型
采用有限元法建立身管组转子-轴承系统动力学模型,如图2所示。

转管炮身管组由身管、炮箍、固定器、导气筒和星形体等组成,零件众多,且形状复杂。为方便建模与分析,在保证身管组质量分布及质心位置相对不变的基础上,简化倒角、工艺槽等对计算结果影响不大的微小特征。
采用考虑陀螺效应的梁理论描述柔性身管的弯曲振动[12]。根据能量法得到梁单元的刚度矩阵K和质量矩阵M,其表达式如下:
(1)
(2)
式中:E为弹性模量;I为截面惯性矩;N为形函数矩阵;A为横截面积;ρ为线密度;L为梁的长度。
由转子动力学得到梁单元的陀螺矩阵表达式:
(3)
式中:Ω为转动角速度;J为极惯性矩,
(4)
式中,R0、R1分别表示内径、外径。
利用动力学原理得到由刚度矩阵、质量矩阵和陀螺矩阵构成的动力学方程:
(5)
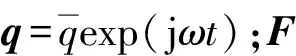
1.3 滚动轴承刚度模型
图3为滚动轴承结构示意图。采用Jones-Harris滚动轴承分析方法建立考虑滚动轴承刚度高速软化效应的分析模型[13]。
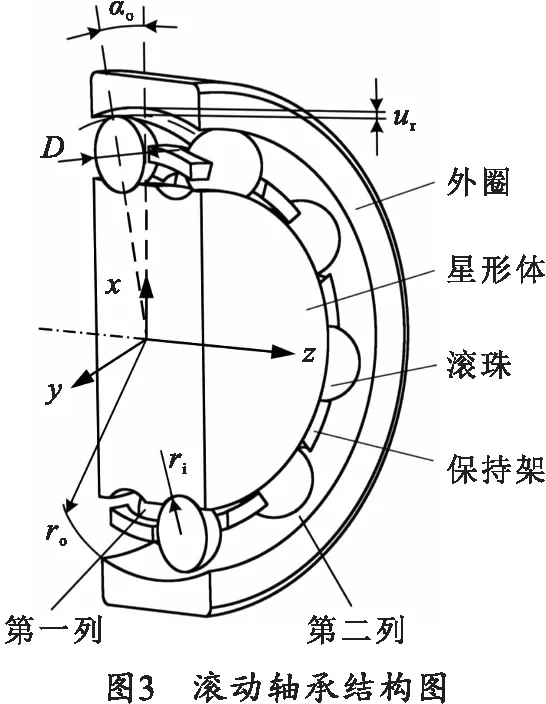
(6)
(Ri-Rb)2+(Zi-Zb)2-(ri-0.5D+δi)2=0,
(7)
式中:D为滚珠直径;ur为径向间隙;ri和ro分别为内、外圈滚道沟曲率半径系数;δi和δo分别为滚珠与内、外圈滚道的接触变形;Ri和Zi由几何关系确定:
(8)
Zi=zi-zo.
(9)
考虑高速旋转产生的滚珠离心力和陀螺力矩,根据套圈滚道控制理论,滚珠在轴向和径向的受力平衡方程分别为
(10)
(11)
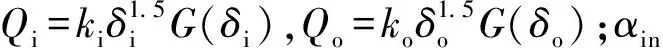
(12)
(13)
式中:dm为节圆直径;mb为滚珠质量;Jb为滚珠转动惯量;β为滚珠偏航角;ω为身管组转动角速度;ωR为滚珠自旋角速度;ωm为滚道角速度。
内圈的受力平衡方程为
(14)
(15)
滚动轴承的二维刚度矩阵为
(16)
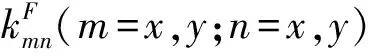
(17)

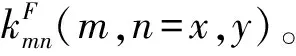
2 结果与讨论
2.1 轴承刚度
某转管炮选用7024C轴承作为身管组支承,其结构和材料参数如表1所示。
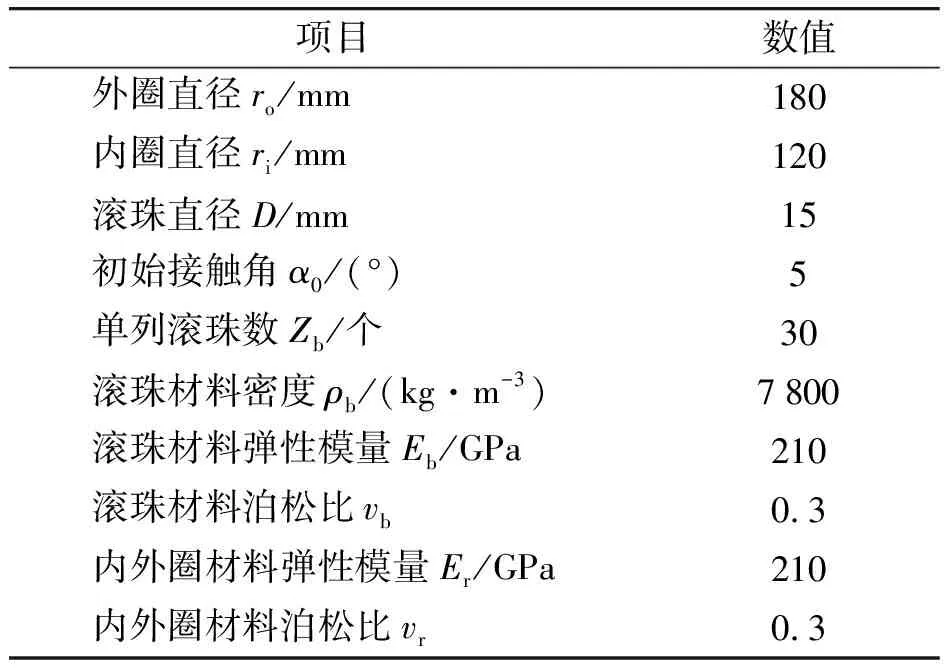
表1 滚动轴承结构和材料参数
设置转管炮身管组转速上限为2 000 r/min,根据所建滚动刚度理论模型计算得到轴承刚度随转速变化曲线,如图4所示。

2.2 身管组模态分析
对模型进行网格划分,考虑到计算内存大小以及计算速度和准确度,对导气筒与身管连接处以及身管组与星形体连接处采用四面体网格,其余部分均采用六面体网格。结构网格整体最大尺寸不超过2 mm,局部较为复杂区域的网格尺寸不超过1 mm。划分后的网格划分图如图5所示,整个身管组模型共划分为425 219个节点,1 311 267个单元。
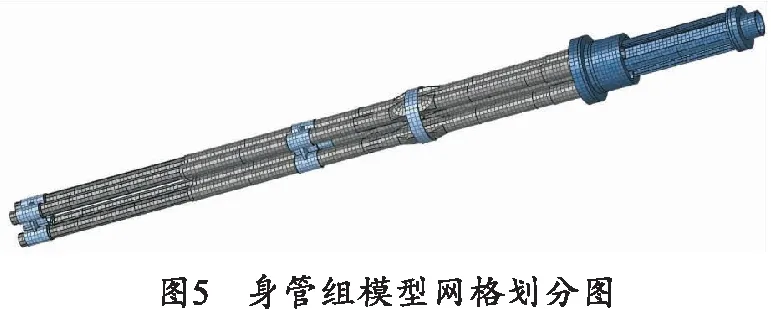
由文献[15]可知,影响系统固有频率和振型的最主要因素为材料的密度、弹性模量和泊松比。某转管炮身管组材料为炮钢,其材料参数如表2所示。

表2 身管组材料属性表
针对身管组的模态分析,将转子及零部件作为附加质量和转动惯量离散到转轴上。各节点是质量集中的部位,利用MASS21模拟转轴上等效的集中质量点,如图6所示。
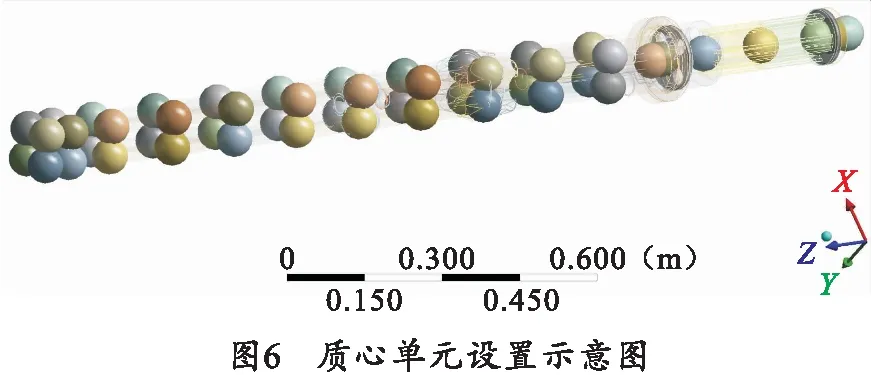
根据身管组的实际工作情况,身管组围绕其中心轴旋转,故对星形体及炮尾处添加圆柱副约束(Cylindrical support),对身管组有限元模型整体添加转速,打开陀螺效应模块(Coriolis Effect);在滚道槽处以及第三支点处添加轴承副,如图7所示。

设置转速为500 r/min,滚动轴承在该转速下的径向刚度为152.63 N/μm。对身管组进行模态分析,前5阶固有频率如表3所示,相应振型如图8所示。
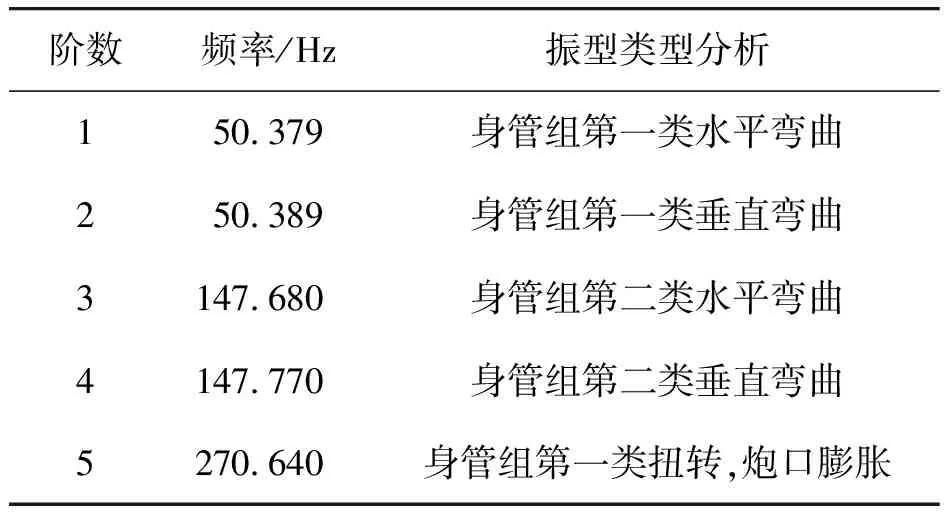
表3 固有频率及振型类型分析
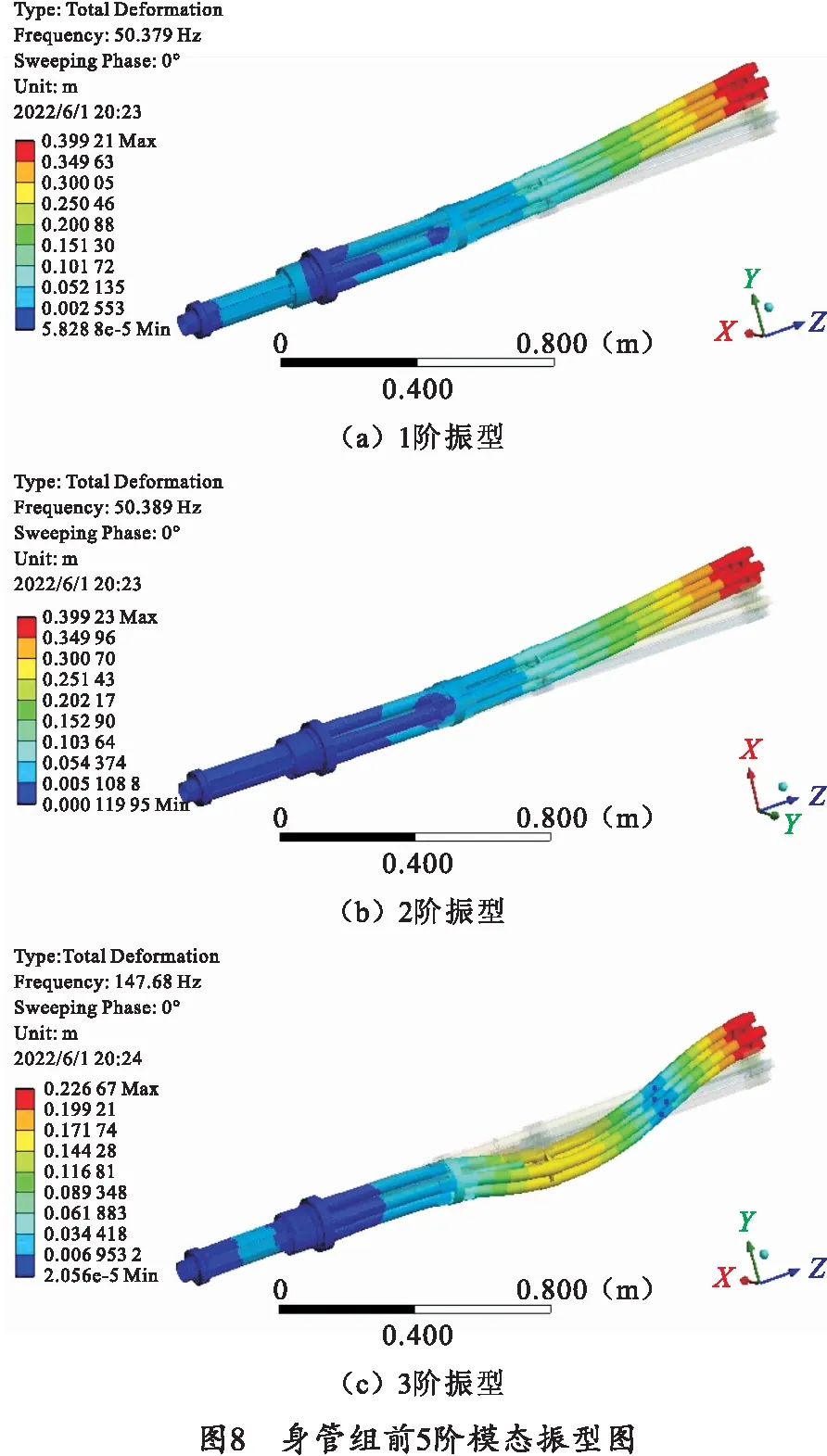
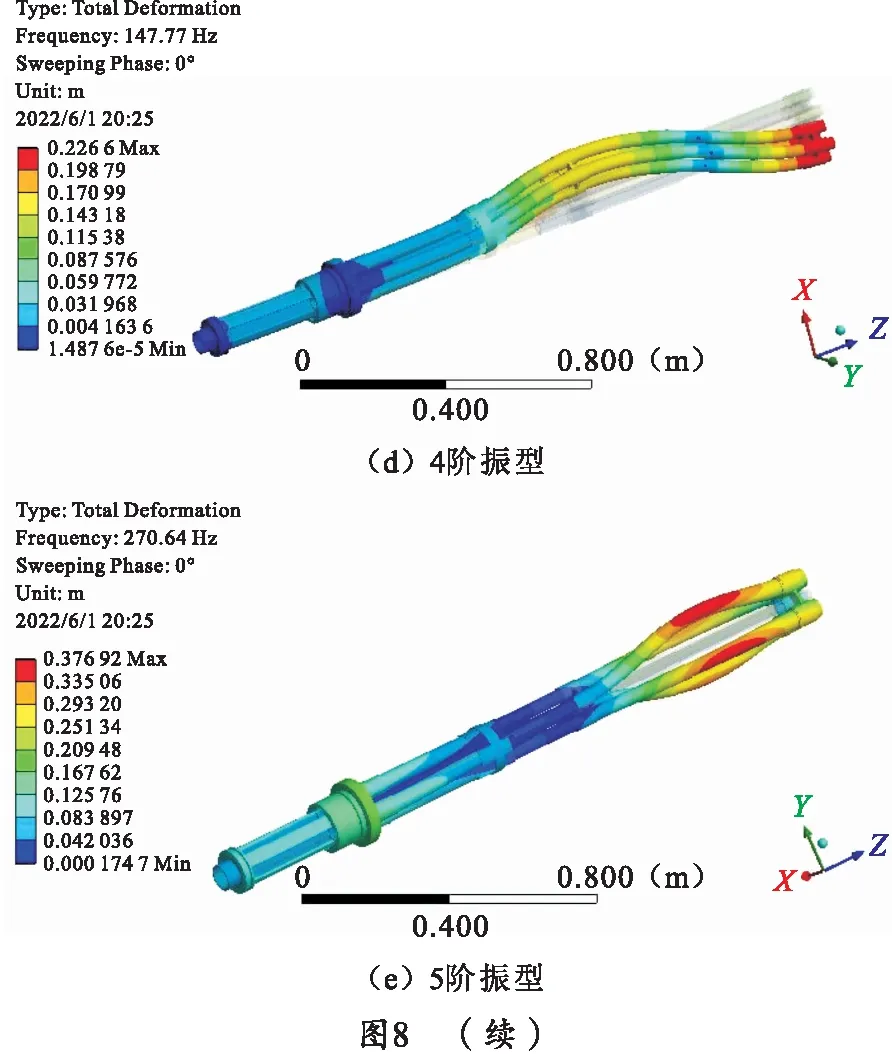
结合表3与图8可知,(a)与(b)振型图分别对应身管组第一类水平和垂直弯曲,即同一固有频率下相互垂直的振型,其固有频率相等,振型方向垂直;同理(c)与(d)振型图分别对应身管组第二类水平和垂直弯曲,即同一固有频率下相互垂直的振型,其固有频率相等,振型方向垂直。
2.3 主要参数对固有频率的影响
2.3.1 转速的影响
将轴承刚度作为转管炮身管组转子-轴承系统动力学分析的基础数据,通过转子动力学求解得到身管组固有频率随转速的变化。在实际测试中,由于低阶固有频率对结构的影响较大,故选取身管组前4阶固有频率进行分析,身管组前4阶固有频率随转速的变化曲线如图9所示。

当转速增大时,身管组固有频率随之减小。当身管组转速从100 r/min升至2 000 r/min时,其前4阶固有频率分别下降了4.22%、3.30%、10.33%和9.95%。
在身管组转动时,其固有频率应避开自动机的转频与射频,从上述仿真结果可以得出,理论上自动机转频从100 r/min升至2 000 r/min,即由1.67 Hz升至33.33 Hz,射频从400 r/min升至8 000 r/min,即6.67 Hz升至133.33 Hz时,身管组前4阶固有频率均避开转频与射频区间,满足安全要求。
2.3.2 径向间隙的影响
在工程应用中,滚动轴承存在径向间隙ur,其大小会显著影响轴承的支承性能,需进一步探究轴承径向间隙对身管组固有频率的影响。
计算不同间隙下的轴承刚度随转速变化曲线,如图10所示。从图10中可以看出,轴承刚度随间隙增大而减小。

转速为500 r/min时,身管组前4阶固有频率随轴承间隙的变化曲线如图11所示,其中负间隙表示轴承压缩量。当轴承径向间隙增大时,身管组固有频率随之减小。当轴承径向间隙由-1 μm升至1 μm时,其前4阶固有频率分别降低了10.86%、10.86%、26.46%和26.47%。
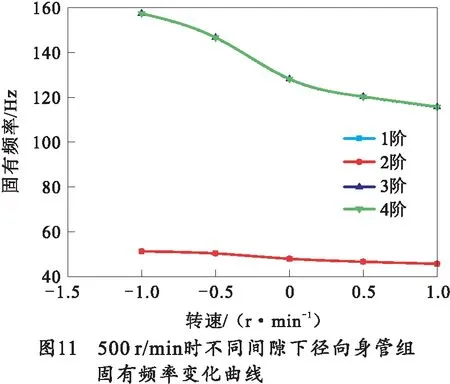
转速为1 000 r/min时,身管组前4阶固有频率随轴承间隙的变化曲线如图12所示,其中负间隙表示轴承压缩量。此时轴承径向间隙由-1 μm升至1 μm,其前4阶固有频率分别降低了10.20%、11.73%、30.02%和31.07%。

以上分析结果表明,当轴承间隙较大时,身管组3和4阶固有频率随转速增大而不断趋近转频与射频区,存在安全隐患。通过预紧技术减小轴承间隙能够有效提高轴承刚度,增大身管组固有频率,通过合理确定固有频率与射速的匹配关系,能够保证射击安全。
3 结论
针对考虑轴承软化效应下不同参数对身管组固有频率影响的问题,采用有限元法建立转管炮身管组转子-轴承系统动力学模型,开展模态分析,得出以下结论:
1)一定设置条件下,当转速从100 r/min升至1 000 r/min,径向刚度出现明显的软化现象,刚度下降了55.02%。
2)滚动轴承结构和材料参数不变的条件下,身管组转速增大,其固有频率随之降低。当转速过大时,身管组前两阶频率靠近转频,3、4阶频率靠近射频,增大炮口扰动,降低了火炮的射击精度。
3)滚动轴承结构和材料参数不变的条件下,轴承径向间隙越大,身管组前两阶频率越接近转频与射频,影响火炮射击精度。为减小扰动,需给予轴承外圈合理的径向压缩量,因为过大的压缩会使轴承温升增加,减少轴承的使用寿命,造成轴承破坏。
