脉冲电源输出电流精度影响因素分析

陈毅，黄凯，闫杰，李菊香，刘承东

(西北机电工程研究所，陕西 咸阳 712099)

电磁发射技术由于拥有高初速、高精度和高隐蔽性等众多传统技术无法实现的优良性能,因此在国防科技领域具有巨大的潜力和重大的战略意义[1-2]。电磁发射技术的初速高精度控制调节能力是其独有的显著优势,其与发射器的电气参数、枢轨接触状态、脉冲电源输出电流精度等方面有着密切的联系[3]。

目前,关于电磁发射初速精度的研究主要集中在发射系统方面。张祎[4]建立灰色系统理论,研究电枢的形状质量和装填过程对发射初速精度的影响。董宗豪[5]设计闭环速度控制器,通过实时监测弹丸膛内运动速度,调整脉冲电源模块放电时刻,实现了发射初速的较高精度控制。陈丽艳等[6]建立电磁轨道炮内弹道模型,采用蒙特卡罗法对各个参数产生的初速误差进行预测。上述研究均聚焦于发射系统,而忽略了对脉冲电源的研究。

脉冲电源是电磁发射的核心组成部分,通过在短时间内释放大量能量,产生强大的电磁力,推动弹丸快速移动。电磁发射是通过控制电流来精确控制发射过程,因此脉冲电源的输出电流精度直接影响电磁发射系统的精度。目前对脉冲电源输出电流的高精度控制方面的研究多集中在脉冲电源的输出电流控制方面。LIU等[7]将脉冲电源和发射器进行联合建模,通过遗传算法控制输出电流波形及其平稳性。唐一林等[8]通过设计的模糊控制器使输出电流波形达到期望电流波形,实现脉冲电源的精确控制。邱燕等[9]虽然研究了脉冲电源器件变化对输出电流的影响,但是仅通过仿真分析了不同模块时序和不同电感大小的影响,对输出电流精度的研究十分有限。

在脉冲电源中,存在很多影响电流精度的因素,为了使脉冲电源达到高精度电流输出的要求,必须分析众多影响因素对输出电流的影响。笔者对电容储能型脉冲电源的输出电流精度的影响因素进行研究,分析脉冲电源的电路原理并基于Simulink建立仿真模型,通过仿真模型分析输出电流精度的众多影响因素,并通过试验验证了仿真分析结果的正确性和合理性。

1 脉冲电源组成及原理

1.1 脉冲电源结构组成

脉冲电源采用模块化设计方法,由脉冲形成单元(Pulse Forming Unit,PFU)组成脉冲形成网络(Pulse Forming Network,PFN),PFN采用并联放电的结构,对同一负载放电[10]。

PFU的原理图如图1所示,主要由脉冲电容器C、大功率晶闸管SCR、续流二极管D和调波电感器L组成。脉冲电容器作为储能元件为系统提供能量,以电场的形式储存系统所需的电能并可以在几毫秒内将巨大能量释放出去[11]。调波电感器的主要作用是调节输出电流的脉冲宽度、控制电流上升时间以及中间储能[12]。半导体功率器件包括大功率晶闸管和续流二极管[13]。大功率晶闸管是半导体开关器件,控制电能的释放与否。续流二极管拥有良好的单向导电性,为电路提供续流回路,延长输出电流的脉宽,此外还能减少电容器反充,提高电容器使用寿命。

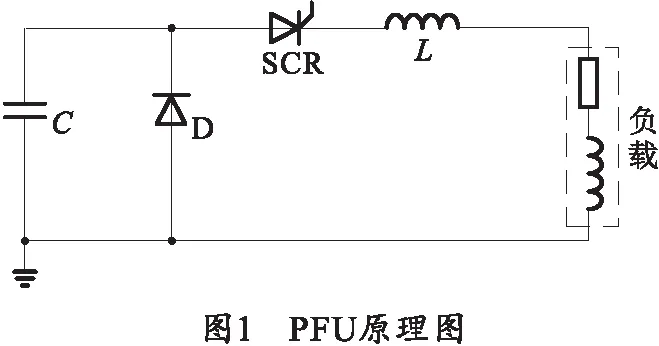
1.2 脉冲电源工作原理

PFU的放电过程可分为两个阶段,第1个阶段为RLC放电电路,第2个阶段为RL放电电路。两个阶段的电路原理如图2所示。

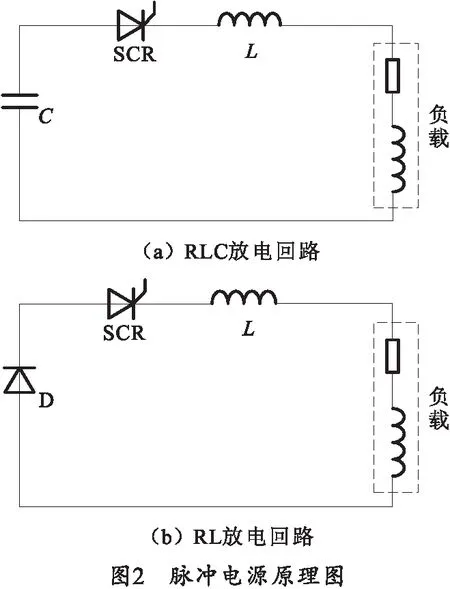
1.2.1 第1阶段

第1阶段为脉冲电容器放电,续流支路截止,该过程为典型的二阶零输入响应电路。根据基尔霍夫电压定律可得:

(1)

式中:uc为电容器电压值;R为电阻值;L为电感值;C为电容值。

又知电容器初始电压为U0,初始电流为0,求解上述齐次微分方程,可得到放电电流i1(t)为

(2)

式中,

(3)

(4)

式中,

(5)

当电流变化率di1(t)/dt=0时,电流达到峰值Imax。

1.2.2 第2阶段

当电容电压降至0后,续流支路导通,此时为第2阶段放电,该过程为调波电感放电,是典型的一阶零输入响应电路。此时放电电流随时间的变化关系为

(6)

由式(4)、(6)可知,脉冲电源输出电流大小与脉冲电源系统中的电容器初始电压、电容值、电感值有关,以下将上述影响因素依次进行仿真分析。

2 仿真模型建立及分析

2.1 PFU输出电流精度分析

Simulink提供了丰富的电力系统仿真数据库,笔者在Simulink中建立PFU的仿真模型,如图3所示。其中,电感器由电感和电阻串联表示,电容器由电容和电阻串联表示,二极管和晶闸管采用模型库原件,负载为电阻和电感串联的恒定负载。

仿真模型的关键参数如表1所示,仿真时间7 ms,步长为1 μs。仿真可得放电电流波形如图4所示。

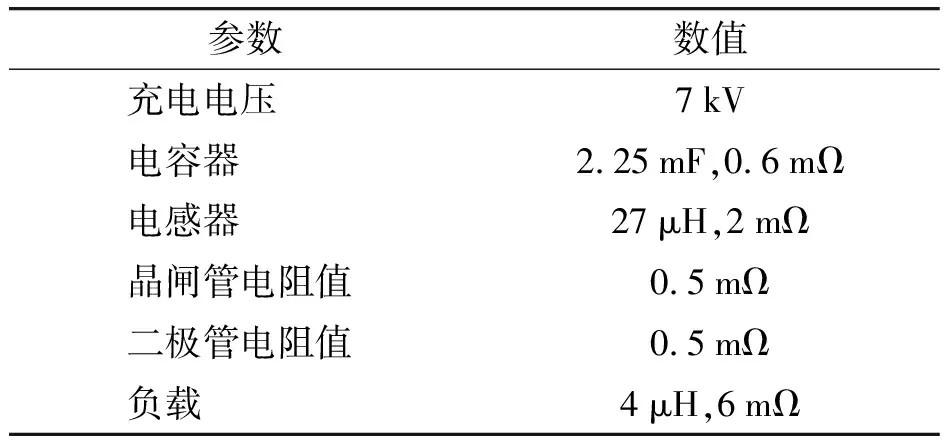
表1 仿真模型主要参数

图4中的仿真波形为理想状态下脉冲电源的输出电流波形,但是在实际使用时,脉冲电源由于充电机的充电精度问题,导致电容器初始电压存在误差;电容器和电感器由于技术限制,在出厂时也会和额定值存在一定偏差;电容器随着使用次数的增多,电容值也会随之下降。综上所述,电容器的充电精度、电容值误差、电感值误差等因素都会影响脉冲电源输出电流精度。由式(4)和(6)可知,输出电流和充电电压为正比例关系,其误差对输出电流的影响也为正比例关系,而与充电电压值的大小无关。当充电电压恒定时,输出电流误差仅受电容值或电感值影响,当充电电压发生改变时,误差计算结果仍保持一致,因此,笔者仅对充电电压为7 kV时的各个影响因素进行分析。

在电磁发射中,电流幅值大小直接影响电磁发射推动力的大小,因此在分析初速精度时应更关注高幅值部分数据。电流值越高对系统的影响越大,电流波形的上半波形为脉冲电流中最重要的部分,因此选择电流值大于电流峰值50%的所有的采样点进行研究分析。引入电流峰值误差(Current Peak Error, CPE)、均方根误差(Root Mean Square Error, RMSE)和平均绝对误差(Mean Absolute Error, MAE)3个指标,用于全面评价输出电流精度。ECPE直接计算电流峰值误差,简单直观地得出了输出电流误差水平。ERMSE由于将误差进行平方,增大了异常值的影响,体现了异常值的数量。EMAE则直接计算误差的绝对值,对异常值不敏感,可以反映误差的真实水平。

ECPE=|Ip-Ip0|/Ip0,

(7)

(8)

(9)

式中:Ip为实际电流峰值;Ip0为期望电流峰值;N表示电流的采样点个数;I为实际电流值;I0为期望电流值;n为采样点。

2.1.1 充电精度的影响

充电机的充电精度造成了电容器初始电压值的误差,通常充电机的充电精度≤1%[14-15]。以下分别对充电电压产生1‰、3‰、5‰、7‰、10‰的误差进行分析,模型中其余电气参数保持不变。仿真可得电流输出波形如图5所示,误差计算结果如表2所示。

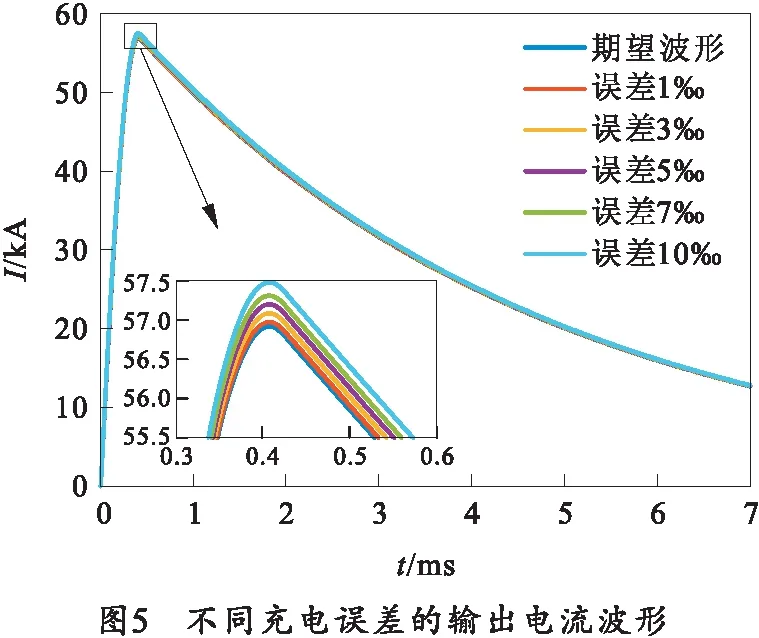
由仿真结果可知,输出电流误差和充电电压误差为线性变化关系,随着充电误差的增大,输出电流误差也随之增大。设充电电压误差为Ue,则可知:

ECPE=ERMSE=EMAE=Ue.

(10)

2.1.2 电容值误差的影响

由于制作工艺的限制,通常电容器会与额定值存在≤3%的偏差。以下将分析在模型其余部分保持不变、仅电容存在不同程度误差的情况下,输出电流精度的变化情况。仿真可得电容值不同误差的输出电流波形,如图6所示,误差计算结果如表3和图7所示。

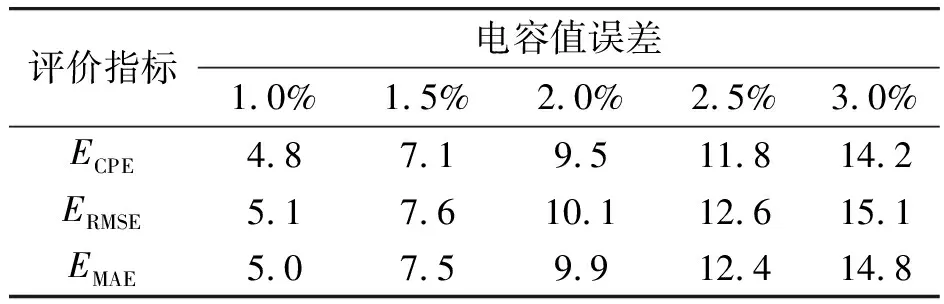
表3 电容值误差对电流误差值的影响 ‰

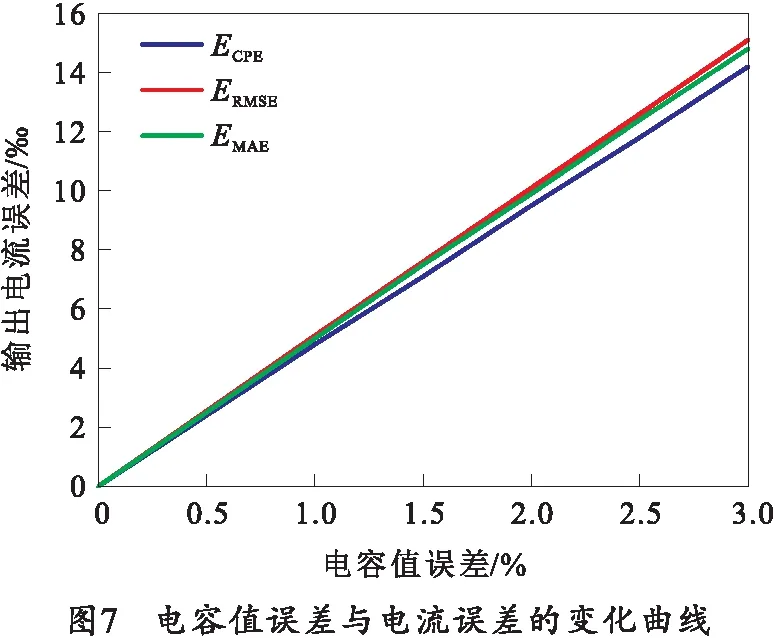
由图7可知电流误差和电容值误差近似为线性增长的关系。设电容值误差为Ce,对试验结果进行曲线拟合,可得两者的函数关系:

ECPE=0.472Ce+0.002 86,

(11)

ERMSE=0.503Ce+0.003 57,

(12)

EMAE=0.498Ce+0.004 29.

(13)

2.1.3 电感值误差的影响

在工程应用中,通常选用的电感器误差在5%以内,分别取电感值误差为1%、2%、3%、4%、5%,当模型其余参数不变时,分析计算其对输出电流精度的影响,输出电流波形如图8所示,误差计算结果如表4和图9所示。由图8可知,当电感误差正向增大,输出电流随之越来越小,电流误差为负向增长的关系。设电感值误差为Le,结果经曲线拟合可得:

ECPE=0.401Le+0.009 52,

(14)

ERMSE=0.256Le+0.004 29,

(15)

EMAE=0.196Le+0.003 33.

(16)

表4 电感值误差对电流误差值的影响 ‰

由上述仿真结果可知,充电精度、电容精度、电感精度和输出电流精度的关系都近似为线性增长关系。此外上述变量对输出电流精度的影响水平从高到低依次为充电电压精度>电容器精度>电感器精度。

2.2 PFN输出电流精度分析

PFN仿真模型由多个PFU模型并联组合形成,如图10所示。PFN模型的仿真参数和PFU仿真模型保持一致,主要参数如表1所示。在工程应用中,充电值、电容值、电感值存在随机误差。当多模块并联同步放电时,会在一定程度上消除系统随机误差,可以提高输出电流精度。此外脉冲电源模块的放电是通过光脉冲触发晶闸管,打开放电回路进行放电。由于触发电路有着定时误差,模块一般不会在设定时刻放电。多模块同步放电时,会存在放电时间不一致的问题。工程设计中常用DSP或FPGA内部的高精度定时器实现时序控制,触发装置的控制精度通常≤±1.5 μs。

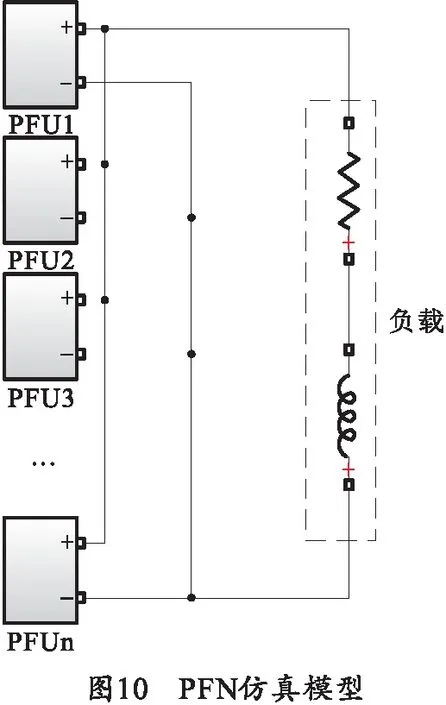
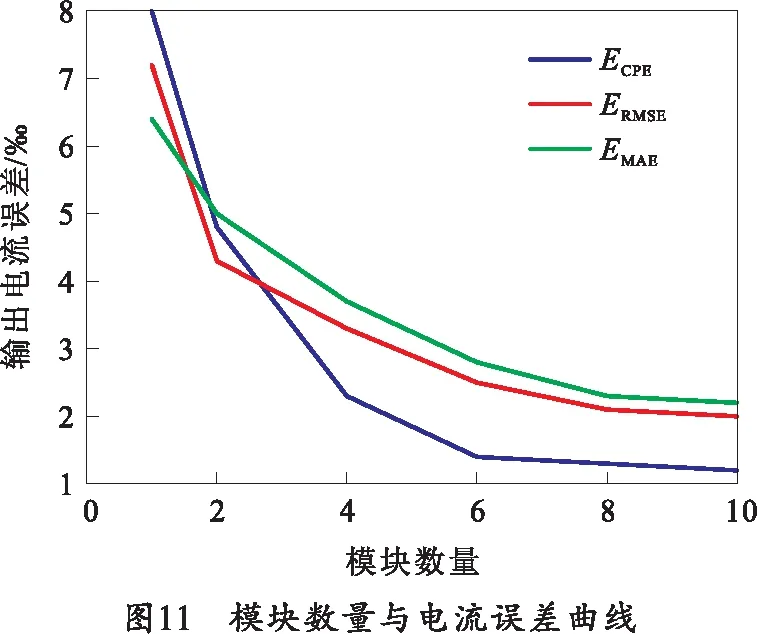
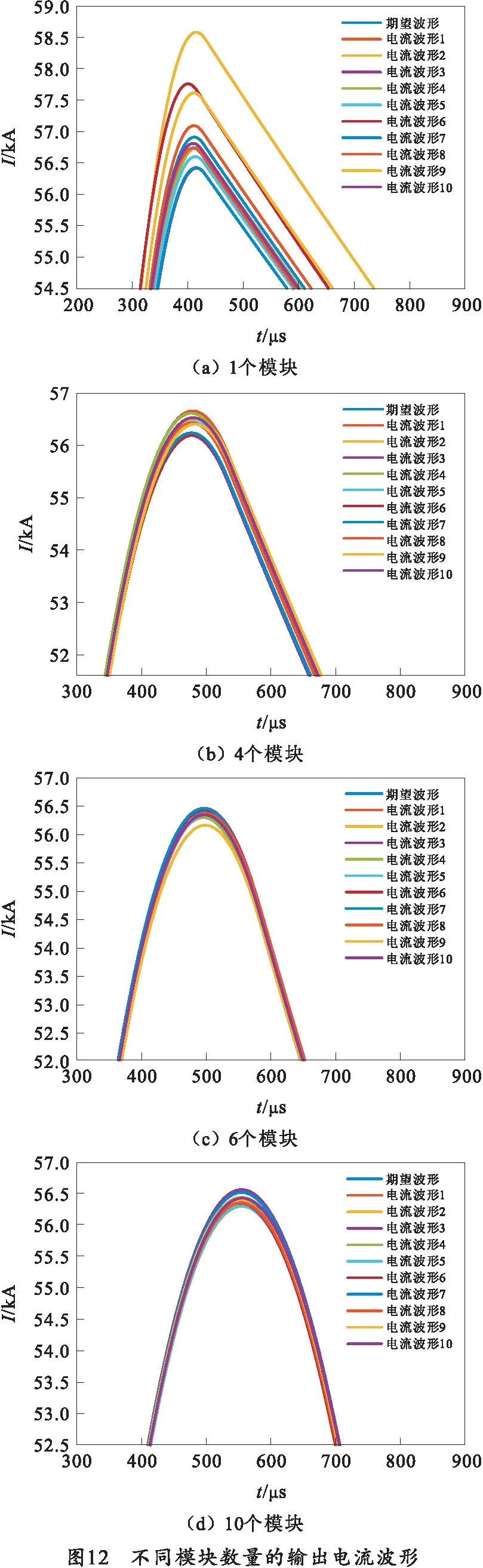
综合考虑上述误差影响因素,设脉冲电源系统的充电精度为3‰,电容器精度为3%,电感器精度为5%,触发延时误差≤±1.5 μs,所有参数服从正态分布。每个器件随机产生误差,使其电气参量随机波动。当PFN的模块数量为1、2、4、6、8、10时,调节充电电压使得输出电流峰值保持一致,分别进行100次仿真,并将所有的误差值进行平均,结果如表5和图11所示,部分电流输出波形的局部示意图如图12所示。由结果可以看出随着模块数量的增多,输出电流误差也随之下降。

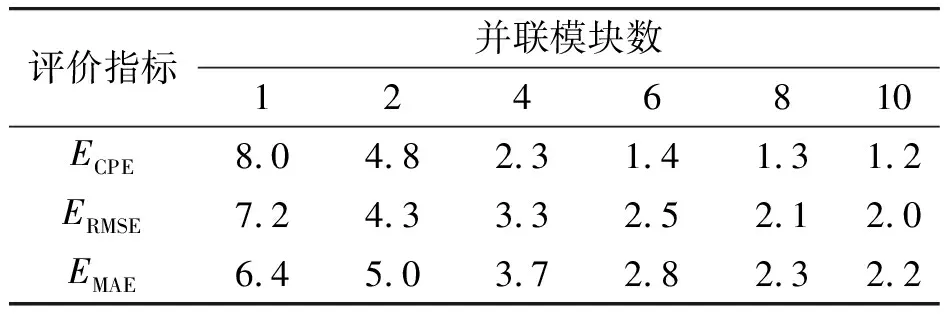
表5 模块数量对电流误差值的影响 ‰

3 试验分析

为了验证上述仿真分析的合理性,随机挑选4个额定电容值为2.25 mF的电容器,经测量电容值分别为2.21、2.24、2.26、2.28 mF。4个额定电感值为27μH的电感器,经测量电感值分别为26.21、26.7、26.87、27.59 μH。然后根据试验需求分别将其和大功率晶闸管、续流二极管等器件组合为脉冲电源模块。将脉冲电源模块与模拟负载进行连接放电,经测量负载值为6.21 μH,12.20 mΩ。采用罗氏线圈测量放电电流,高压差分探头检测充电电压。试验现场如图13所示。

3.1 PFU输出电流精度试验

3.1.1 充电精度

将2.26 mF电容器和26.87 μH电感器组合为脉冲电源模块,通过高压差分探头检测充电电压,分别充电至不同电压值并放电,放电电流波形如图14所示,输出电流误差如表6所示。

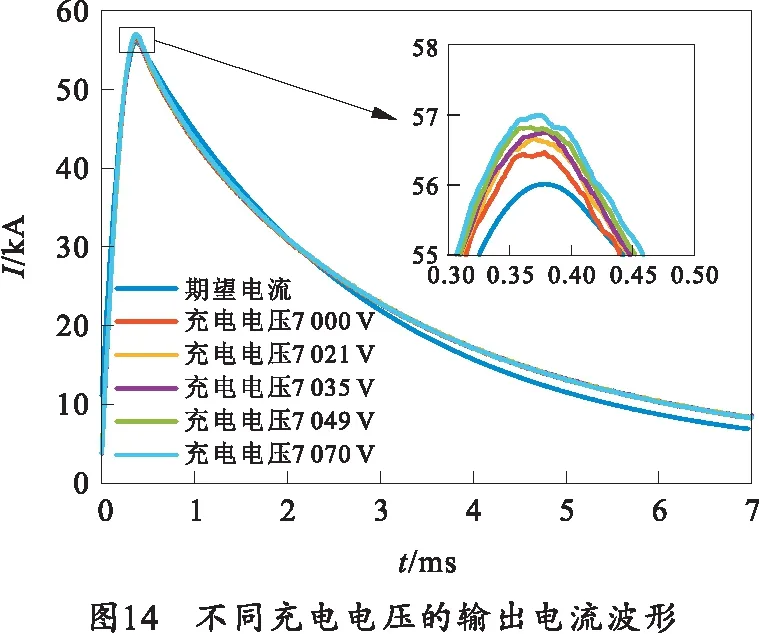
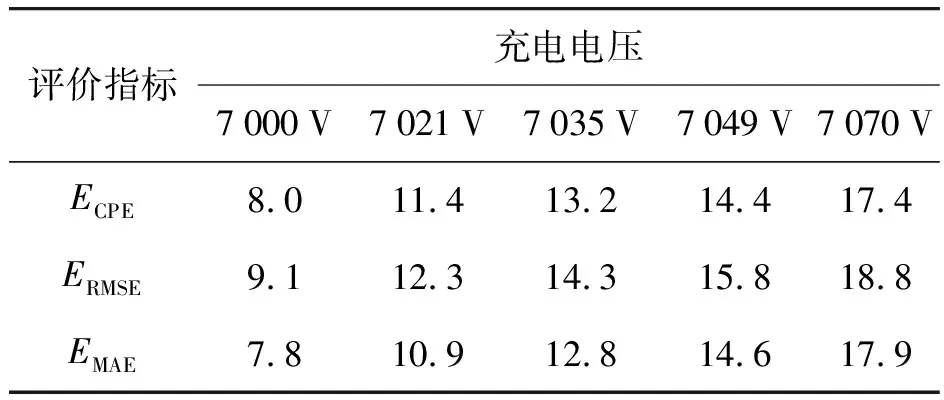
表6 充电电压及其输出电流误差 ‰

3.1.2 电容值误差

将26.87 μH的电感器和4个电容器依次组合为脉冲电源模块,控制充电电压为7 kV。放电电流波形如图15所示,误差统计如表7所示。

表7 不同电容值下的输出电流误差

‰

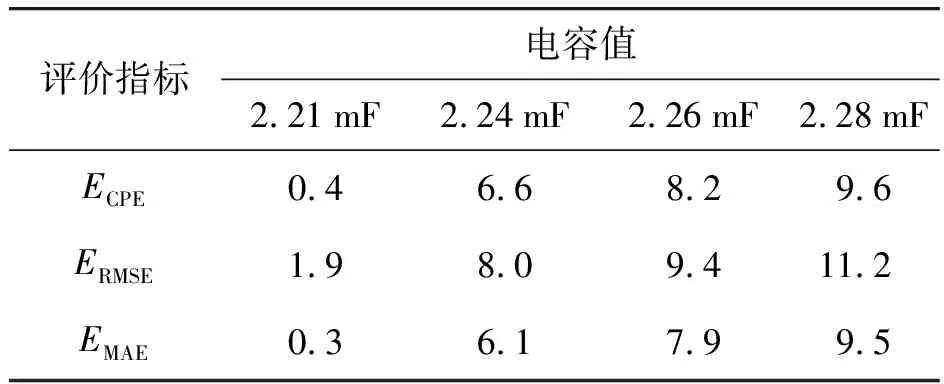
3.1.3 电感值误差

同理,将2.26 mF的电容器4个电感器依次组合为脉冲电源模块进行试验,放电电流波形如图16所示,误差如表8所示。

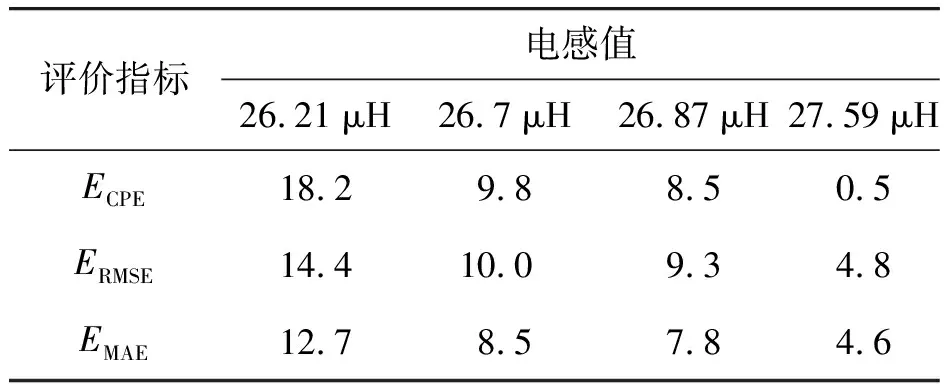
表8 不同电感值下的输出电流误差 ‰

上述试验结果表明,充电精度、电容值误差、电感值误差的影响程度和仿真值相近,且充电精度对输出电流精度的影响程度最高。

3.2 PFN输出电流精度试验

将所有器件随机组合为4个脉冲电源模块,对放电回路中的电气参数进行测量,主要参数如表9所示。首先对4个模块依次进行试验,4个模块的输出电流波形以及通过额定值仿真所得期望电流波形如图17所示。分别计算每次试验和期望值的偏差,结果如表10所示。

表9 试验中主要电气参数

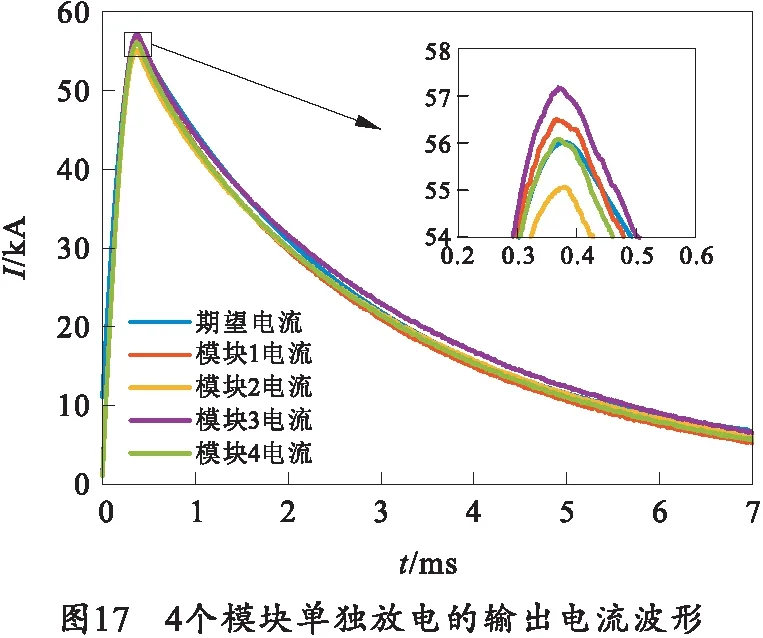
表10 4个模块单独放电的输出电流误差 ‰

再将上述4个电源模块并联,同时对负载进行放电,改变充电电压使得输出电流峰值保持一致。实测电流波形如图18所示,计算可得输出电流误差ECPE=3.5‰,ERMSE=4.2‰,EMAE=4.9‰。

上述试验结果和仿真结果相比,输出电流误差变化趋势一致,且分别验证了充电电压、电容值和电感值这3种影响因素产生的输出电流误差波动幅度和仿真结果相近。除此之外,试验结果还体现了脉冲电源多模块放电电流精度高于单模块平均输出电流精度的特征。

4 结束语

通过对脉冲电源放电电路的理论分析,得到输出电流精度的影响因素有充电精度、电感精度和电容精度等。结合工程实践,可知同步放电的模块数量也会对输出电流精度造成影响。为了分析上述变量对输出电流精度的影响,分别建立了PFN和PFU仿真模型并进行分析计算。此外为了定量评价输出电流精度,引入了ECPE、ERMSE、EMAE3个评价指标。

仿真和试验结果表明,充电电压精度对输出电流精度的影响最为显著,电容值和电感值的影响相近,但电容值的误差影响更为突出。充电电压精度虽然影响最大,但是在工程应用中精度控制水平较高。虽然电容器、电感器对输出电流精度的影响占比较小,但由于工艺材料等限制,难以实现高精度制造,对放电电流的影响反而较大。此外当单模块并联组网为脉冲形成网络时,随着模块数量增多,可抵消部分误差,有助于提高精度。

笔者全面分析了脉冲电源输出电流精度的影响因素,通过理论仿真和试验相结合的方式验证了各个因素对输出电流精度的影响,为脉冲电源满足电磁发射高精度电流输出的应用要求奠定了基础。