基于深度学习的数学教学策略研究

李余芳

【摘要】深度学习，即为教师科学引导学生进行知识的自我深度理解，学生自主循序解决复杂难懂问题的过程即为数学核心素养构建的过程.深度学习即是实现课程改革、发展核心素养的有效路径.本文对高中数学三角函数深度学习策略开展研究，旨在以此方式为教师开展系列教学时提供更具价值的参考标准，从而提高学生综合能力，培养学生高阶思维.

【关键词】深度学习；高中数学；三角函数

深度学习并非一蹴而就的，而是循序发生的过程，需要教师循序引导，带领学生进入最佳状态，开展系列学习.同时，高中三角函数内容更是高考的重点内容，更需要教师持以足够的耐心，引导学生实现深度学习.

1 巧设教学目标，把控教学方向

基于深度学习的数学教学设计时，首先，教师需精细化、深入性研究教材内容及课程标准，制定相匹配的教学目标.新课程标准明确指出：促进学生发展的系统教学，需要教师持以整体性教学观念，立足于整体视角之下设立教学目标.深度学习将更注重知识的系统整合及有机构建，同样更强调教师整体观念.教师只有具备一定的整体教学观，方可构建起更为系统、全面、整体的数学课堂，保障学生在自主学习过程中，构建起更为完整、全面的知识链条、知识架构.因此，基于深度学习的数学教学，需立足于整体性角度上，帮助学生掌握系统知识.

教学目标确立之前，教师需确立该单元系统.单元大小并没有统一规定，为此，教师可通过教材内容出发，也可以要从数学核心知识角度出发，确立单元内容.单元教学目标的确立既需要整体性单元目标，又要细化课时目标.整体性单元目标则是涉及到学生素质培养、数学思想培养、高阶思维培养等诸多方面，课时目标则是前者的具体化内容，是在整体方向之下，依据相关教学内容制定的学生所需掌握的能力、知识、素养目标.因此，在教学目标制定过程中，需综合教学课程标准，把控教材相关要求，注重学生对其学科知识、思想方法的掌握理解，并在系统单元落实中更科学地实现教学任务.

例如 以“三角函数”单元教学为例，在进行教学目标设计时，需明确三角函数在教材内容占比及其重要程度.在确立基本三角函数相关教学内容，就其三角函数系列内容即可设置相关的教学目标：（1）掌握三角函数系列预备知识：明确扩充角、周期，理解弧度制；（2）以圆周角度出发，深度探索正余弦函数相关定义及基础形式，对其正切函数予以类比研究，并掌握y=cosx、y=sinx在0，2π的相关图象表示及具体性质；（3）结合具体实例深入研究：y=Asinx（ωx+φ）的具体图象变化，明确其中的参数意义，回归简单实际的问题，精细刻画该事物变化模型；（4）系统研究三角函数恒等关系：二倍角、同角、两角和差.

2 整合数学教材，更新教学内容

教材既为教学主体，同样也是学习内容基础载体.教学核心内容都是根据教材内容所制定，同时教材也是国家标准规划的，所面向群体复杂，个体差异性显著，因此难以兼顾到各个学生、各个学校的实际情况.为此，为了能够将教材实际使用价值得以充分发挥，教师就需对课程内容予以系统整合.首先，需综合考虑到教材外部要素，即学校资源、教师资源、学生资源.教材整合旨在更好地服务于学生，因此，教材整合内容需依据学生具体接受程度来设定.普通学生则是以数学基础内容为重心，重在激发学生学习兴趣.拔高学生侧重在拓展，实现针对性进步；其次，教材内部因素，例如教学实例及教学情境的开发.教材课本实例同情境内容都是年年延续，久未改变.其中很多实例题目同现实生活完全脱节，数据信息也未及时更新，极易引发学生的学习陌生感.因此，教学准备阶段，教师需深度挖掘该教学案例同教学情境背后的内容，充分保留经典，在不改变原则的基础上适当修改.

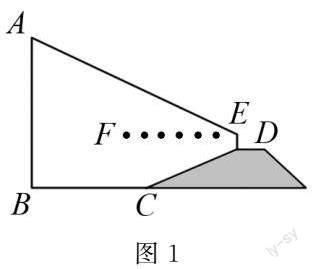
例如 针对三角函数典型例题，如图1所示，垂直于水平面的三角形建筑物，为测量AB高度，小明自建筑物底端B点出发，走52km，走到C点，而后沿CD前进，直至到达顶坡D点处，BC=DC，在该D点位置进行测量，DE高度8km，E点处测得该建筑物顶端A点仰角为27°，点A，B，C，D均为同一平面内，斜边CD坡度比为i=1∶2∶4，求AB高度.

该案例教学中，可以发现步行52km不太现实，所以极易引發学生的不现实感.为此，教师需及时更新相关单位、数据内容，将其更换为52m，方可让该例题增添真实感.此外，教师还需适当丰富教材内容，不仅仅是增添些许相关知识内容，更要适当融入数学文化、数学素养等此类精神层次内容.该内容的增添，将引导学生更深入理解该数学内容的实际价值，促使学生及时获取数学知识，培养数学能力，丰富数学解题经验.以三角函数教学为例，教师为了让学生更明确三角函数的使用意义，可在课堂教学时，适当讲解三角函数的发展史，让学生感受古人智慧，让学生感受到探索数学知识过程中的惊喜.

3 预评估教学推进，激活学习状态

3.1 开展预评估模式，明确最近发展区

依据相关数据调查显示，大多学生在学习新知识时会联系旧知识.教师作为学生学习的引导者、促进者，更要在日常教学时，帮助学生在新旧知识串联中，搭建有效纽带.在此工程中，教师需明确学生原有认知水平，既可对新知识起到一定的促进作用，也能起到些许的启发作用.因此，教学准备阶段，教师就需落实预评估工作，以此方式深度了解学生知识水平、知识储备量，并密切关注学生极易出错的环节.此外，预评估工作也将更进一步明确学生最近发展区.深度学习将紧密围绕极具挑战性主题，然而其挑战“天花板”与学生之间的距离时，教师教学设计环节的基础依据，因此，教师需保障学生发展在科学范围内推进.

预评估内容主要有教师评估、学生自评两方面组成.教师评估则是依据教师教学经验及对学生的了解情况进行评估，为了提高评价精准度和评估效率，教师即可通过大数据、互联网手段进行全面分析.例如，一些网络批阅作业的软件，它不仅更精细化分析学生考试各个环节得分情况，也将同学生以前考试成绩进行对比分析，立足于诸多维度全方位剖析学生具体学习情况.学生自测则需依靠学生的自主学习，教师可设置三角函数的相关导学案，引导学生循序了解自己的预习效果，明确学习难点，及时开展针对性优化.

3.2 循序激活状态，创设主动学习氛围

首先，教师需明确深度学习主体在于学生，学生学习参与度将直接决定学习效果.为了提高学生的参与度，就要善于激发学生内部学习动機，在实际教学中，教师则要创设出主动学习课堂氛围.在此过程中，教师需明确，教学氛围质量并非以课堂热闹程度为标准，而是以学生实际行为状态同当前学习情境的配合度为前提.学生主动学习习惯也并非是一朝一夕即可养成的，而是需要教师在日常教学中有意识地培养.学生主体意识将直接决定学生主动学习的效率和学习频率，只有学生将自己作为学习的主人翁时，才能自然形成主动学习氛围，教师则需及时开展系统调节.如若学生并不具备主体意识，主动学习氛围也是表面形式，将在教师要求下成为被动.因此，教师教学出发点即为学生个人需求，让学生参与教学过程就具备决定权，强化学生学习过程的主人翁意识.

其次，教师则注重民主师生关系的建立.师生关系作为社会关系最为特殊复杂的一种，将是让学生放松状态，实现深度学习的重要影响因素.教师要积极与学生构建起民主型关系，创设出互助、平等、开放的相处模式，尽可能地多鼓励、多表扬学生，增强学生自信心，激发学生兴趣，以此方式，将帮助学生快速进入深度学习状态.

4 构建教学情境，实现深度学习

4.1 立足现实条件，呈现真实体验

开门见山式的教学，较难以激发学生的积极性.因此，急需构建有效有趣的情境，帮助学生快速进入状态，以此状态不仅激发学生的学习兴趣，也将快速引导学生思维开展深度思考.首先，教师需立足于现实条件，带给学生更为真实的体验.综合深度学习内涵及数学核心素养相关要求，高中数学系列教学必须在真实学习情境基础上开展，引导学生在基础知识储备之上，挖掘学习内涵，自主透过生活情境获取价值信息.教师需综合考虑数学学科本质特性，并以学生实际生活为基础，构建出更为真实的教学情境，为学生后续学习问题提供有效“脚手架”，帮助学生掌握更深层次知识内容，理解更复杂的概念定义，开展深度学习.

例如 在三角函数：y=Asinx（ωx+φ）图象理解时，教师即可将生活中摩天轮经历构建教学情境.为此，教师可以附加视频丰富学生的体验感.通过以国内最大摩天轮“南昌之星”为例，该摩天轮最低点距离地面7m，直径153m，共计设有60个太空舱，各个太空舱最多可容纳8人.忽略其他因素影响，将其摩天轮运转活动视为匀速运动，每旋转一周需历经30分钟，上舱起点即为该摩天轮最低点，经过t分钟后抵达B点，求B点距地面的高度H=f（t）.以此方式，将带领学生进入更为真实的现实世界中，让学生放松神经，沉浸于教师所设置的情境问题中自主探索.

4.2 巧设教学问题，引申深度思考

浅层学习则是低阶基础性思维的思考过程，更倾向于死记硬背记忆方式掌握相关知识，难以依据实际问题的具体开展情况，灵活运用法则公式及其他数学知识.深度学习则是在其低阶基础性思维基础之上，指向高阶思维，将透过数学问题挖掘相关概念原理，并在问题解决的过程中始终持以积极乐观的态度.以此对比可见，深度学习核心在于问题的解决.因此，教师不仅要注重教学情境的真实度，更要全面挖掘、深入分析教材内容，同时设置更具启发性思维的深度学习相关问题.并且，问题的设置需具备层次性特点，引导学生思维发散得以由低至高，层层递进，层层发散.因此，层次性不仅体现为该问题的表现难度，更体现出其启发性和灵活度.

例如 在学习“三角函数”时，教师可抛出“现实生活中，运用三角函数‘勾三股四玄五’定理的现象有哪些？”面对该问题，学生首先会懵住，这时教师则要循循善诱引导学生，“勾三股四弦五”作为勾股定理的典型例子，其原理在于直角三角形中，两条直角边分别为3、4时，其斜边则为5.在实际生活中，常在工程案例中应用，是验证两条线是否垂直的有效措施，鉴于人工操作误差较大，因此距离较大时常用仪器检测，距离较小则利用勾股定理检测.该问题看似较为简单，但是略加思索就需要综合考虑多方面因素，既在其知识层面上引出三角函数内容，也凸显勾股定理特征，能力层面上，也将引导学生利用数学思维解决生活问题.

5 结语

综上所述，基于深度学习的数学教学策略.首先，教师需精细化、深入性研究教材内容及课程标准，制定相匹配的教学目标；其次，需综合考虑到教材外部要素，即学校资源、教师资源、学生资源.学校资源，即为综合学校特点及当地特色，开发国家相关课程，以此多样化、多角度地培育学生；再次，教学准备阶段，教师就需落实预评估工作，以此方式深度了解学生知识水平、知识储备量，并密切关注学生极易出错的环节；最后，需立足于现实条件，带给学生更为真实的体验.

参考文献：

[1]朱嘉怡.基于深度学习的高中数学建模教学研究[D].上海：上海师范大学，2022.

[2]李保臻，孟彩彩，巩铠玮.基于深度学习的高中数学教学设计：基本要求及优化策略[J].内江师范学院学报，2022，37（02）：1-5.

[3]谭云.基于深度学习的数学课堂教学研究[D].长春：长春师范大学，2020.

[4]罗颖.基于深度学习的高中数学课堂教学设计研究[D].南昌：江西师范大学，2020.

[5]薛志宏.高中数学教学中促进学生深度学习的研究[D].开封：河南大学，2020.