聚力三“点”：提升微视频资源开发的效度

江苏省盐城市滨海县实验小学 陆立海

奥苏伯尔“认知同化论”认为，有意义学习的过程是学习者利用认知结构中的原有知识，吸收和融合新知识的过程。盐城市林玉平名师工作室围绕“基于数学思考的资源开发的研究”，设计了四大教学板块（典型问题、关键环节、学法点睛、举一反三）并录制教学微视频，着力解决学习中的重点、难点、热点等问题，为学生的学习建构、拓展思维提供资源，为学生自主学习创造条件。在微视频的关键环节，应该促进学生建立新旧知识间的联系，建构新体系，实现学生对知识的透彻理解。针对如何达成这一要求，提升微视频开发的效度，笔者认为可聚力以下三“点”：

一、多元表征，找准已有经验的生长点

表征是指学生对学习的知识在头脑中进行记录、储存、改组、呈现、表达的方式。表征的方式有很多种，如语言、符号、图形、操作等。多元化呈现助推数学理解、多元化勾连建构认知结构、多元化外显引发思维可视，可以更好地赋能学生数学思维自然生长的力量。制作微视频时可采用多元表征方式，帮助学生找准已有知识经验，理解题中信息，建立问题的解决架构，降低认知的难度，为学生的自主学习提供条件。

（一）图形表征，助力学生理解

高度的抽象性是数学的一个显著特征。对于部分数学命题，学生虽然多次阅读，但仍然 “不知所以”，无法理解题目中的信息，很难找到已知量与未知量之间的关系，或者原有的知识结构超出了学生的认知水平，学生很难找到解决问题的入口。录制这样的微视频时，可用图形表征出已知信息或隐含信息，引导学生观察、解读、审视，将原有的知识结构转化成学生较为熟悉的知识结构，以便学生拟定解决问题的方案。

如制作“三角形的内角和”微视频时，有一个典型问题：一个等腰三角形，底角是顶角的2倍。这个三角形的顶角是多少度？从题面上看，这道题似乎只有1个信息，实则有3个隐含的信息：①三角形有三个角；②三角形的两个底角相等；③三角形的内角和是180°。用图形表征出已知的信息和隐含的信息，题中的数量关系就非常清晰了。

制作微视频时还可以用图形表征思路流程，引领学生不断地追问“由什么得出什么”与“要求什么需什么”，培育学生分析与综合的思维能力。

如图1为13-8的“破十法”解题结构图；图2为常见的两步计算的实际问题分析法与综合法的思路图。

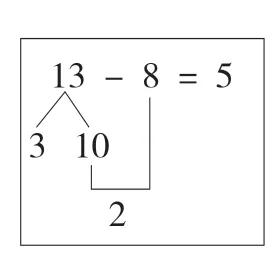
图1

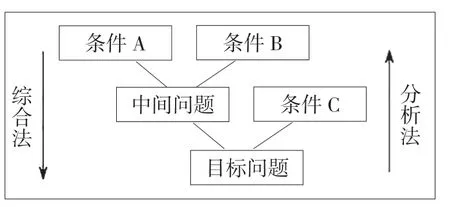
图2

（二）动作表征，助力学生感悟

学生认知结构的初始阶段就是动作表象。面对新问题，教师可适当引导学生通过动作表征，体验事物的发生、发展过程，更好地把握数量之间的关系。制作视频时，要突出学生的主体性，引导学生在具体场景中直观感受，从而促进学生思维走向深入。

如 “相遇问题”微视频中设计的典型问题：李叔叔和王叔叔分别从各自的家中同时出发，沿着同一条公路相向而行。李叔叔骑自行车每小时行驶12千米，王叔叔骑电动车每小时行驶20千米。行驶了2小时后，李叔叔与王叔叔之间的距离正好是10千米。李叔叔家和王叔叔家可能相距多少千米？讲解时，教师首先引导学生用两只手表示两个人，分别从两边相向移动，正确理解“李叔叔与王叔叔之间的距离正好10千米”的含义，可能还没有相遇，两人之间的距离是10千米；也可能已经相遇，继续前行后，两人之间的距离是10千米，从而找出不同的思路及答案。

表征的方式还有很多种，如符号表征、语言表征、数字表征等，每种表征各具特点，各有优势。学生在学习研究不同的数学内容时，也会采用不同的表征方式，视频资源开发应注重多元表征之间的关联，强化表征之间的转换，促进学生对数学知识的理解和解决问题，实现学生能力的提升。

二、问题驱动，跨越认知发展的障碍点

好的思路来源于过去的经验和以前获得的知识。但仅仅靠存储于大脑中的图式结构，不足以使自主认知同化，还需要使用一些特殊问题或材料去暗示、去引导、去链接信息，将新知识要点与已有的认知结构中特别相关的部分联系起来。数学微视频的设计，应以问题驱动数学思考，让学生经历体验、理解和变通的过程，促进学生有效建构知识和解决问题。

（一）溯源式提问，感悟知识的类属关系

类属学习主要有两种形式：派生类属学习和相关类属学习。无论是派生类属学习，还是相关类属学习，都是将新知识纳入原有认知结构中。解这类题时，一般可采用溯源式提问。所谓溯源式提问，就是抓住新命题和原有认知结构的联系，教师通过提问，引导学生找出它们之间的类属关系，用原有的解题思路解决现有问题。设计这类视频，关键是引导学生先行观察题目的特征，找出类属于哪个知识模型，再根据数学模型去解题，实现认知的同化。

如在 “乘法分配律的推广使用”的微视频中，教师首先出示了一道典型题目：用简便方法计算16×32-16×2。乘法分配律原有模型为（a＋b）×c=a×c＋b×c，由此派生出模型（a-b）×c=a×c-b×c，而简便计算16×32-16×2又是这个模型的具体化。教师提问：仔细观察这道题，你发现了什么特征？学生找出都有共同的因数后，教师再追问：按照乘法分配律，可以怎样算？学生回答可提取共同的乘数16，再将另外两个数32和2相减。教师还可以溯源综合算式的意义，提问：16×32表示什么意思？16×2呢？引出32个16减去2个16，可以简化成（32-2）个16，即通过（32-2）×16来计算。

（二）对比式提问，找准知识的上位观念

总括学习与类属学习相反，原有知识为从属观念，新知识为上位观念。在这种条件下，利用原有知识结构解题，就存在用来修饰、限定原有知识结构的内容，被扩展到新知识（上位观念），使学生形成认知错误的情况。教师通过对比式提问，让学生找出从属观念和上位观念的差异，了解出错的症结，便于学生进行知识同化，更准确地解题。学生掌握上位知识的本质属性后，可进一步追寻、提炼出从属观念的“特殊”现象与本质，丰盈学生的认知。

如 “三步混合运算式题的计算”的典型问题：计算240÷6－2×17和51－36÷3＋2。240÷6－2×17应该先算乘、除法（横线上的部分），且这两步可以同时算。但有学生会将上位知识“先乘除、后加减”忽视，而专注于“两步同时算”，以至于解第2道题时出现错误。录制微视频时，教师可提问：51－36÷3＋2应先算什么？先算减法和加法，行吗？为什么第1道算式可以“两步同时算”，第2道算式不可以呢？让学生观察画线题目得知，第2道算式是三步运算的一般形式（承接关系），而第1道算式是三步运算的特殊形式（并列关系），从而有效地区分一般和特殊的关系。

（三）迁移式提问，把控知识的组合结构

当学生的新概念或新命题与认知结构不存在类属关系，也不产生总括关系，而它们存在着某些共同的关键特征时，奥苏伯尔称这样的关系为并列组合关系。在录制微视频时，对具有的内部结构、解题策略存在相似、但又不是相同知识点的内容，教师可采用“迁移式提问”，引导学生进行尝试、探索、发现。有效的迁移式提问，需要教师有意识地建立起新命题和原有知识结构间的关系，唤醒学生的原有认知结构中能同化新知的内核。

如在“十几减8、7”微视频中，教师先通过提问引导学生回忆十几减9是怎样计算的，从而让学生自行推算十几减8、7。学生推算出结果后，教师再通过视频展示平十法、破十法、想加算减法，促进学生正向迁移能力的提升。

三、多向思考，聚焦思维进阶的撬动点

所谓多向思考，就是从尽可能多的角度去考查、分析同一个问题，使学生思维不局限于一个模式和一个方面，以便学生深刻理解知识、拓宽视野、发展思维。可以是执因问果，顺向思维；也可以由果寻因，逆向思维；还可以由此及彼，横向思维。小学数学资源的开发，开展异同、分合、进退等思维方式的训练，既能发展学生的顺向思维、逆向思维，也能发展学生的横向思维。

（一）找异同，强化思维的深刻性

数学思维的深刻性是指数学活动的抽象程度和逻辑水平。思维的深刻性本质上是指深度的概括程度，集中表现在学生能全面且深入地思考问题，运用逻辑思维整体把握和问题相关联的所有条件，围绕问题的实质深入钻研，正确、简洁地解决问题。视频录制要注重培养学生数学思维的深刻性，可以引导学生从新旧知识的各种关系中找出异同，理清知识结构，把握问题脉络，实现思维的进阶和问题的解决。

如微视频“两位数减一位数（退位）”，教师出示了这样一道典型题目：计算86-8。教师在学生自主探索的基础上，分享了三种方法（如图3）。

图3

在此基础上，通过比较可以发现，三种方法都是将新问题转化成熟悉的计算题来计算，但又有不同：第一种方法将被减数拆成一个整十数和十几的数，用十几减一位数，再相加；第二种方法直接从被减数中拿出一个十来减一位数，再相加（破十法）；第三种方法是从被减数中先去掉一位数的部分（平十法）。这样对比，让学生感受到计算方法的差异性，增强了学生对算法的理解。

（二）会分合，增强思维的严密性

分与合，是重要的数学思想。用分与合的思想讨论问题，具有很强的综合性、探索性和逻辑性，一般分为四个步骤：（1）根据题设条件，明确分的对象；（2）确定分的标准，做到不重复、不遗漏；（3）逐类进行讨论，得出各自的结论；（4）综合各类别的结论，得出原设问题。简而言之，就是化整为零，各个击破，再集零为整。用分与合的思想解题时，要引导学生发现并发掘题目中的隐含的“分”的条件，确定“分”的标准。对学生来说，这是一种考验，需要教师多引导，帮助学生实现问题的解决、意识的增强和能力的提升。

如微视频“三角形的三边关系”中设计了典型问题：把一根长14厘米的吸管剪成三段（取整厘米数），围成一个三角形，可以怎样剪？首先根据“任意两边之和大于第三边”，得到最长边需要小于7厘米；又因为14÷3=4……2，得到最长边需要大于4厘米，因此最长边可以分为6厘米、5厘米两种情况进行讨论。当最长边为6厘米时，另外两边分别有三种情况：6厘米和2厘米，5厘米和3厘米，4厘米和4厘米。当最长边为5厘米时，另外两边为5厘米和4厘米。至此，符合题目的四种剪法全部被找出。

（三）知进退，体会思维的灵活性

华罗庚先生说：“善于‘退’，足够地‘退’，‘退’到最原始而不失重要性的地方，是学好数学的一个诀窍。”换而言之，退是为了更好地进。退是策略，进是目标。在解题或新的数学学习活动中，学生往往不善于从心理表征的“原点”处入手，总是局限于所提供的信息。录制微视频时，教师可适当分享一些“退”的策略，如从一般退至特殊，从抽象退至具体，从整体退到局部，从高维退至低维，等等，从而增强学生思维的灵活性，提升学生解题的灵活度。

如微视频“数的奇偶性”设计的典型问题：任意连续的6个自然数，它们的和是奇数还是偶数？教师先采用了举例法，“退”到计算6个连续的自然数，从“1+2+3+4+5+6=21”提出猜想，并通过其他举例进行验证。再在举例的基础上进一步分析，无论是“奇数＋偶数＋奇数＋偶数＋奇数＋偶数”，还是“偶数＋奇数＋偶数＋奇数＋偶数＋奇数”，都是3个奇数和3个偶数相加，从而得到最后的结论。教师还从6个自然数的奇偶周期排列特征出发，先退到求证一个周期“一个奇数加一个偶数”的情况，再推算出3个周期的情况。

除了以上所述，基于数学思考的数学微视频资源开发的设计策略还有很多，如文化熏陶、思想育人、多元评价等，需要教师全面地审视、整合和优化，以更优质的微视频资源服务于学生的学习、认知、建构。