那场“几个几”的争论风波——记“乘法的初步认识”一课

浙江省杭州市求是教育集团 江 萍

一、回放——意外的争论

某日，笔者执教“乘法的初步认识”一课，在顺利地完成新课之后，出示了一道练习题（见图1），请学生思考看到了几个几。没想到，就是这样一个问题却引发了一次意外的课堂争论。

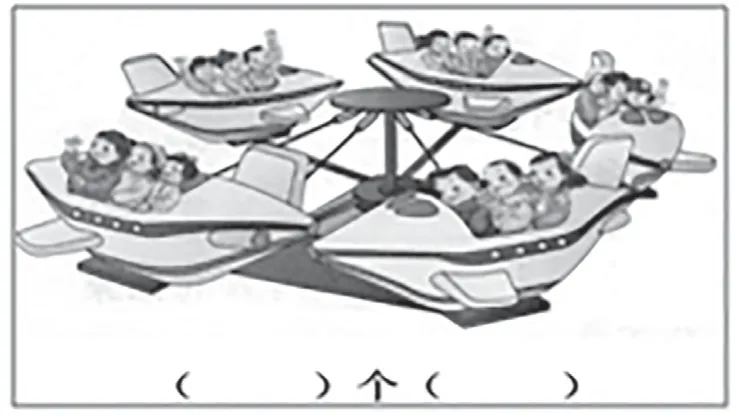
图1

师：从这幅图中你看到了几个几？

生（齐）：应该是5个3。

生1：应该是3个5。

师：到底是5个3还是3个5呢？谁来说说理由？

生2：我认为是5个3，因为图上一共有5架飞机，每架飞机里坐了3个人，所以是5个3。

生2的发言清晰、到位，笔者在心里暗自为他叫好。于是，笔者反问生1：你有什么想说的？

生1：我还是认为3个5。

师：为什么？

生1：每架飞机里都坐了3个人，所以是3个5。

生1的坚持到底让笔者吃惊不小，同样他毫无逻辑的推理也让笔者无从下手。究竟是什么让他的想法如此坚定？短暂思考几秒之后笔者决定把这个问题抛给全班学生。

师：我们来听听大家的意见，同意3个5的举手（只有“生1”一位），同意5个3的举手（除了“生1”，剩下的同学都举手了）。

师（对着“生1”）：全班只有你一个人是这么想的，现在你认为自己的答案一定对吗？

生1（很坚定）：对。

师：那好，谁愿意与他辩论一下，看看谁能说服谁？

很多双小手高高举起，笔者邀请了生2作为“5个3”答案的代表与生1进行辩论。

生2（理直气壮）：你这个5表示什么意思？

生1：这个5表示5架飞机。

生2：那每架飞机里坐了几个人？

生1：3个人。

生2：那你数一数，一共有几个3？

生1：有5个。

生2：那不就是5个3吗？

生1：好吧！5个3是对的，但3个5也是对的。

生1终于承认5个3是对的，这让一旁“观战”的笔者长吁一口气，但他的后半句“3个5也是对的”又让笔者纳闷不已。

生2：你不讲道理啊，你自己好好看一下图。

生1（振振有词）：这幅图是表示5个3，但5个3和3个5的答案都是15，我以前就知道一个乘法算式表示两种意思，所以5个3、3个5应该都对。

生2（据理力争）：没有图，一个乘法算式是表示两种意义，但现在这道题有图，需要看吗？

生1：……看图的话应该是5个3。

持续了5分钟的争论，终于在生1说出5个3后画上了句号。笔者暗自庆幸问了“到底是几个几”，让生1的想法浮出水面。同时也感谢生1，他的坚持己见让这场意外的争论异常激烈，同时也让笔者的思考渐渐深入。

二、聚焦——问题出在哪

图意这么清晰的一道题，竟然会引发学生对“几个几”的争论，这让笔者始料不及。学生为什么会有“因为答案一样，所以表达的意思也一样”的错误理解？问题究竟出在哪？

（一）问题一：抽象概括“几个几”有难度

课前笔者曾在班上做过一次前测（见图2），请学生填一填几个几并用算式来表示。从学生的答题情况来看，全班42人中全对的有22人，答题正确率为52.4%，近三分之二的学生都能用加法正确列出算式，三分之一的学生会用乘法算式3×4或4×3来表示。学生答题中的主要错误是填写“（ ）个（ ）”。19.1%的学生填了（12）个（熊猫），16.7%的学生填了（12）个（4），11.9%的学生填了（6）个（6）。这说明在没有教师指导的前提下，请学生用几个几表示同数连加还是有一定难度的。学生因为无从下手，所以才会出现（12）个（熊猫）这样的词语填空；因为概念模糊，才会出现（12）个（4）、（6）个（6）这样的答案。由此看出，概括“几个几”并不像我们想象得那样简单。

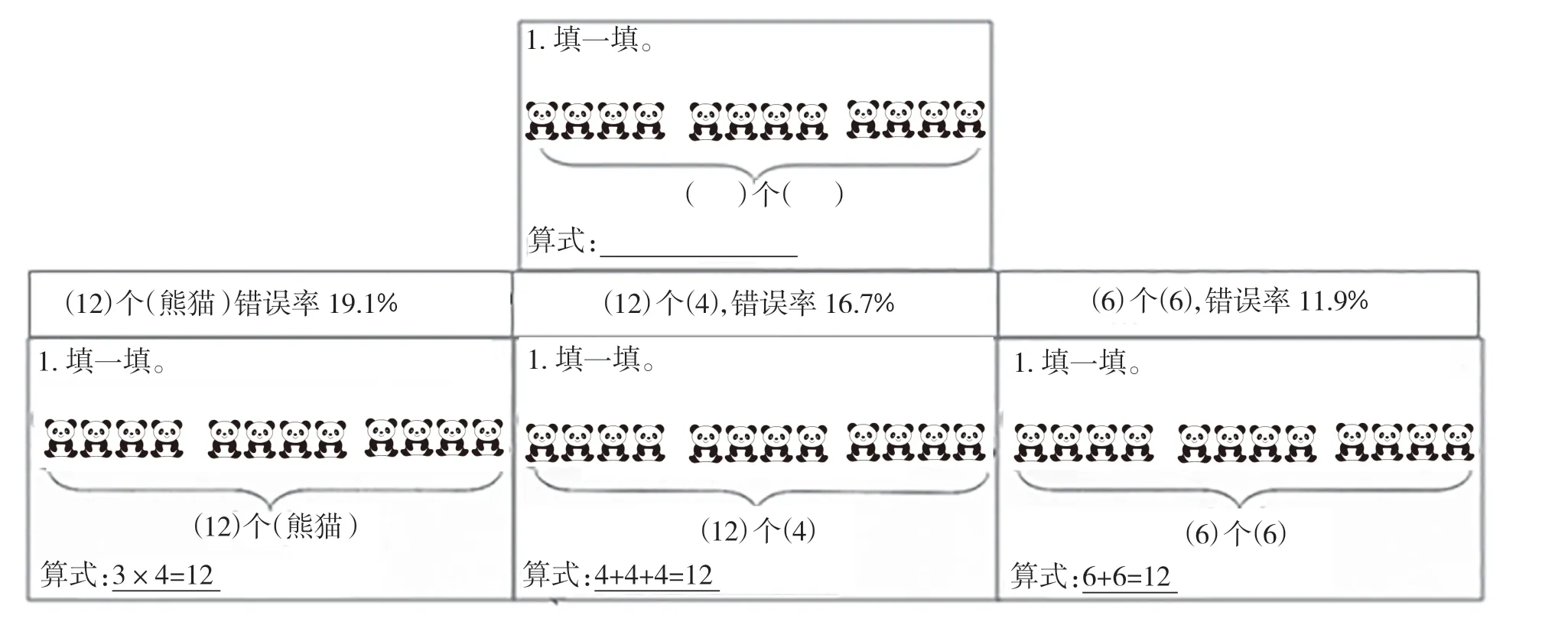
图2

（二）问题二：理解乘法意义“生搬硬套”

课后，笔者与生1进行了深入的交流。他告诉笔者，在新课学习之前他就已经认识了乘法，知道一个乘法算式表示两种意义，能熟练地背诵乘法口诀。因此，他凭借自己“先学先知”的优势，想当然地认为3个5、5个3都对，根本没有仔细读图。可见，对乘法意义的一知半解让学生在解决问题时生搬硬套。在教学实践中，我们发现学生或是出现像生1这样的情况，或是认为“脱离了情境的乘法算式就只表示一种意义”。在前测中，笔者曾设计过这样一道题（见图3），调查情况显示：看到算式3×5，大部分学生将其理解为3个5相加，80.9%的学生只选了一个答案，只有19.0%的学生做对此题。无论“生1”还是“前测现象”，都提醒我们让学生真正理解乘法意义，形成对乘法现实模型的认识是非常重要的。

图3

（三）问题三：多样化表征难以灵活转换

我们知道，让学生通过说一说（几个几）、写一写（加法算式与乘法算式）、画一画等活动，实现语言表征、符号表征、图形表征之间的相互转化，能帮助学生进一步理解乘法的意义。而多样化表征之间的灵活转换是学生学习的难点之一。在课堂教学中，“生1”的问题就出在“从图到式、从式到图”的转换。如果他能清晰地知道“从图到式”并不简单等同于“从式到图”，可能也就不会有课堂上的“坚持”。这也让笔者想起了前测中的一道题：画图表示算式3×4的含义。根据调查结果显示，能用图表示出算式意义的学生占35.7%，而这些学生所画的图大部分表示的是3个4，没有一人能完整地表示出乘法算式表示的两种含义。在错误的图示中，部分学生只会用3×4的结果表示算式的含义，还有11.9%的学生完全不会做这道题。通过检测，说明课前学生对乘法意义的理解是不到位的，同时也可以看出让学生理解多种形式表征特别是图形表征乘法意义的迫切性与必要性。

以上三个问题的存在也让课堂上的那场“争论风波”成为情理之中的事情。

三、实践——课堂是关键

面对争论，我们究竟应该怎么办？在教学中，我们是否可以做这样的尝试？

（一）新课展开：围绕几个几

新课以算式4×5导入（见表1），一方面可以找到学生真实的学习起点，了解学生课前对乘法意义的理解程度；另一方面通过由式到图的过程，又可以引导学生学会从“图式对应”的角度理解“几个几”。新课的展开以“小棒搭成的正方形” 作为研究素材，从5个4到4个4、3个4、2个4、20个4、100个4的不断变化，让学生清晰地理解图、式之间的关系。通过板书的进一步梳理，将几个几、加法算式、乘法算式联系在一起，突出了乘法意义的本质，让学生体会到用乘法算式表示的便捷。

表1 新课展开环节设计

（二）练习巩固：清晰几个几

练习巩固的第一道题是“式与式的转化”（见表2），练习中既有像6×6这样加数与个数相同的习题，又有同一乘法算式3×5或5×3表示两种不同含义的题目，从而让学生对算式中的“几个几”的认识更加清晰。练习巩固的第二道题“由图到式”，呈现了教材中游乐园的主题图，让学生结合现实情境自主抽象概括几个几，并列出加法、乘法算式，沟通图与式的关系。练习三则举一反三“从式到图”，鼓励学生自主地运用多种方式表征算式，从一种意义的图形表征到两种意义的矩形模型表征，不断拓宽学生的思路，深化学生对乘法意义的理解。

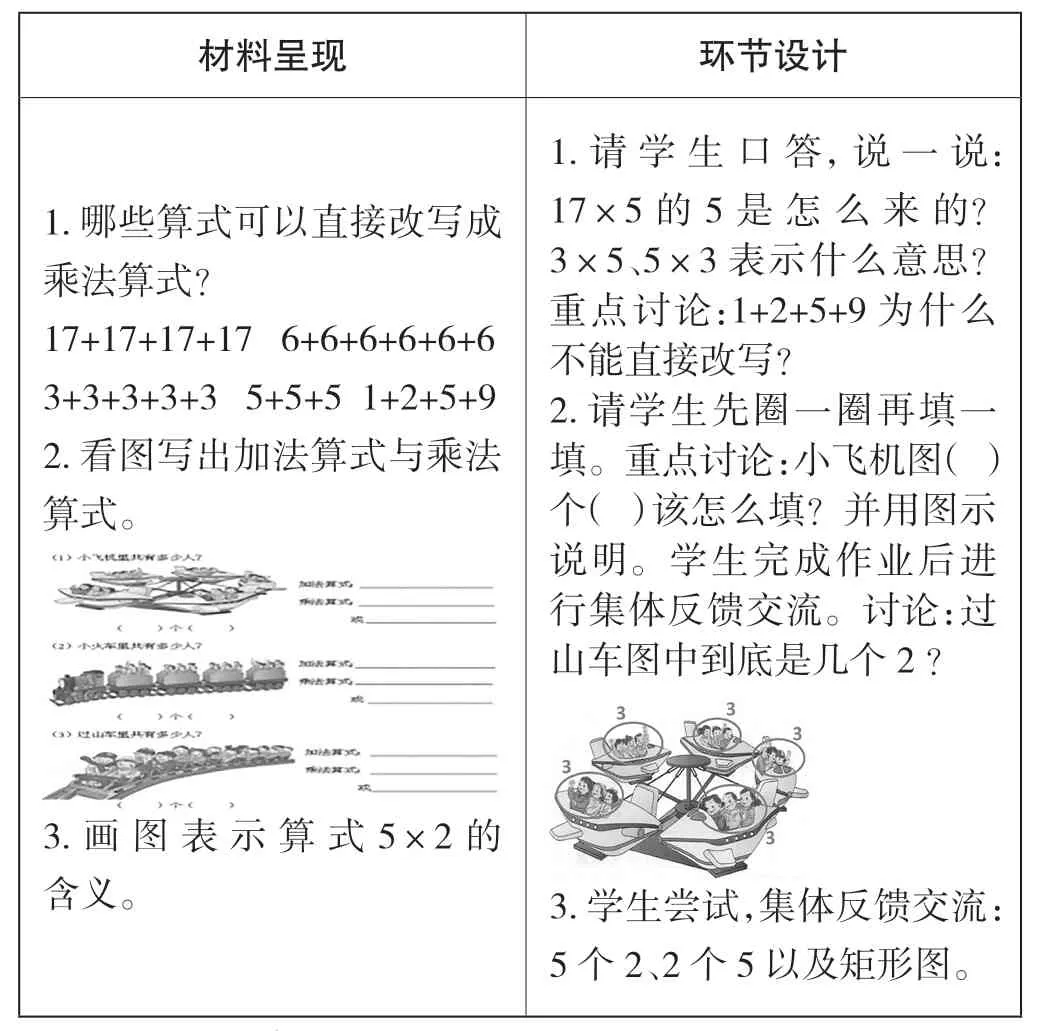
表2 练习巩固环节设计

（三）拓展提升：深化几个几

拓展提升部分的第一题（见表3），在学生自主表征算式意义的基础上通过一列一列、一行一行变化的矩形模型，引领学生不断思考：增加了几个几？现在是几个几？学生在思辨中丰富对乘法模型的认识。拓展提升的第二题则通过让学生列举生活中的乘法，感受乘法在实际生活中的作用。在这一环节中，教师没有浮于“找乘法算式”的表面，而是引领学生理清“几个几”，深入思考每个乘法算式表示的实际含义，提升了学生的思维抽象水平，在“生动”与“深刻”中做出有益的尝试。

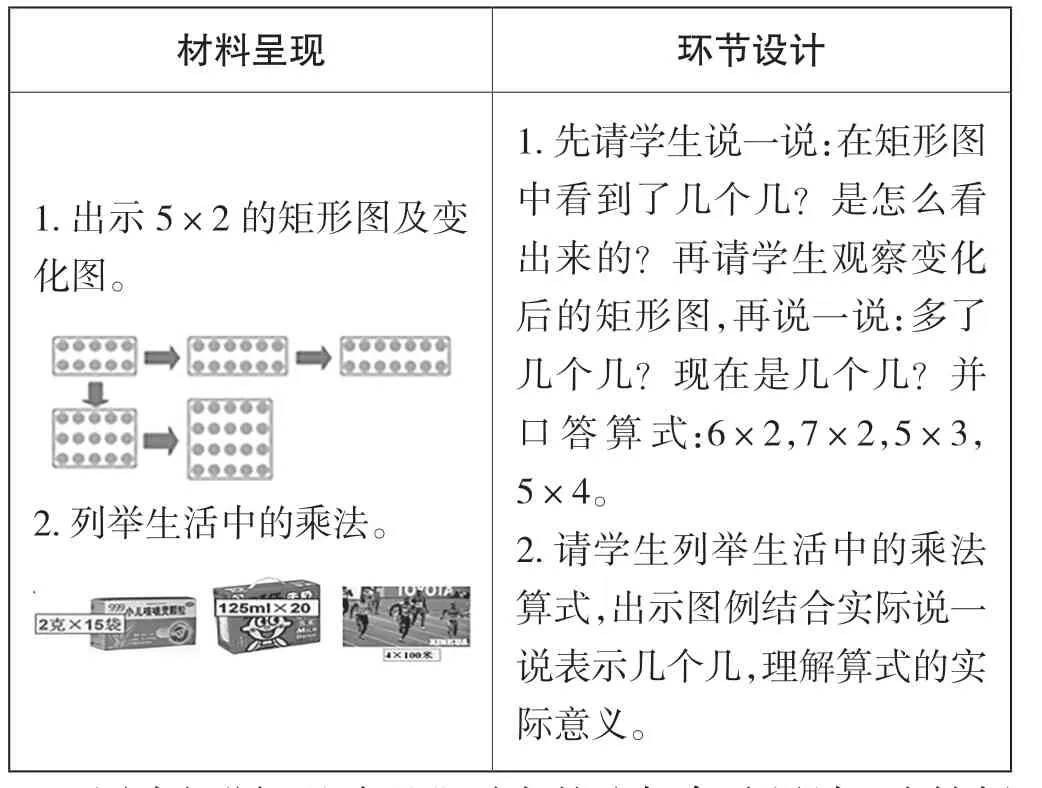
表3 拓展提升环节设计

因为问题“几个几”引发的这场争论风波，让教师对学生的了解更进了一步，对乘法的教学思考也更加深入。实践也再次证明：问题基于学生，教学才能真正精彩！