旋转水密封性能优化设计分析

赵洪林 赵永乐 董淼

摘 要：新型旋转密封件在机械密封技术领域做出性能突破，其结构主要包括O型圈和密封环，O型圈套设在密封环的外壁上，密封环的外壁周向设有泄压槽。该密封件在工作时设置在密封沟槽之间，在设备工作时，工作介质会流动到密封件端面两侧的结合面的间隙内，密封件阻隔密封件端面两侧的工作介质，使间隙内的工作介质只能在各自的一侧端面间隙内流动。同时通过在密封环的外周设置泄压槽，改变O型圈和密封环外壁的接触的密封表面，使O型圈和密封环的接触面积减小，调整O型圈和密封环外壁的接触的密封表面受外界偏压作用时密封环的接触压力分布。最终实现改善密封效果，提升密封件使用寿命。

关键词：旋转格莱圈；O型圈；密封环

中图分类号：TU506                                 文献标识码：A                                文章编号：2096-6903（2023）01-0039-03

0 引言

密封件是机械结构中常用的用于密封的零件，格萊圈是密封件中的一种，常用于径向旋转密封。格莱圈由一个丁腈橡胶O型圈及填充聚四氟乙烯密封圈组合而成。目前市场上格莱圈的进口品牌以特康密封圈为主。进口格莱圈成本高，市场上其他成本较低的国产品牌的格莱圈，往往密封性能低于进口格莱圈[1]，为了获得成本更低、质量更优的产品，特此对旋转格莱圈作出技术改进。

1 原因分析

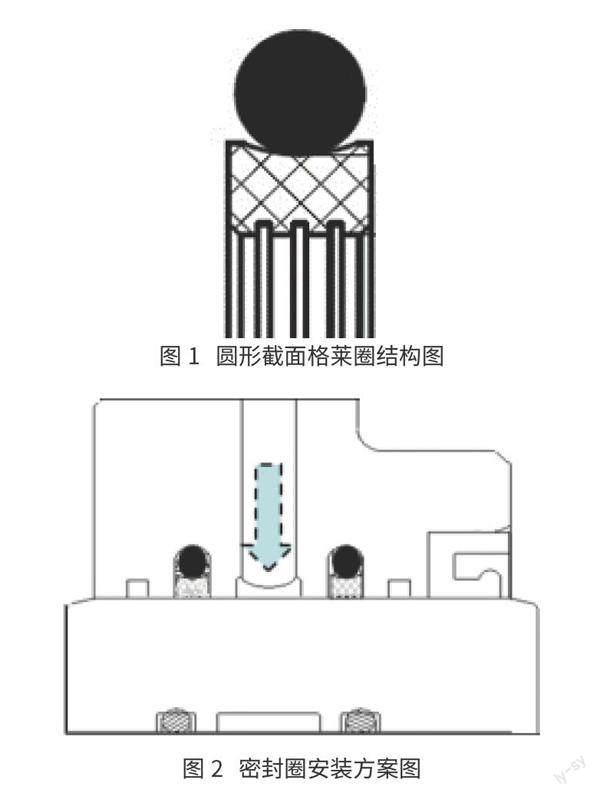
橡胶密封圈密封的原理为密封面最大接触压力大于工作压力即实现密封，旋转格莱圈结构形式如图1所示。格莱圈在实际使用过程中使用条件较复杂，多为交变载荷，同时承受高温偏载作用。经计算旋转格莱圈要实现密封， O形橡胶密封圈压缩率为15%～30%。由于橡胶圈在长时间处于较大压缩率的状态下，橡胶圈受材料所限，温升情况加剧，进而会加速材料老化，导致弹性降低，产生永久破坏，无法保压，最终失去密封效果。

密封圈工作安装时装配关系如图2所示。两道旋转格莱圈安装至沟槽中，其中O型橡胶圈与沟槽相接触，密封环与下方旋转隔套相接触，O型圈自身与密封环相接触。

2 改进设计

本次改进从以下3个方向，来提升旋转格莱圈性能：①降低O型圈压缩量，提高O型圈使用寿命。②解决密封圈承受偏置载荷时，对密封环的偏磨影响。③改善密封圈启动时的稳定性。

2.1 降低O型圈压缩量

根据密封面最大接触压力大于工作压力即实现密封，要实现密封，矩形密封圈的压缩率应为8%～14%，O形密封圈压缩率应为15%～30%[2]。经试验验证，在相同工况及作业环境条件下，改变单一压缩量会降低密封圈老化情况，因此矩形圈的老化速度相比O形圈会相对较慢。

2.2 解决密封圈偏磨问题

当密封圈界面转变为方形时，方形角配合沟槽圆角，可为密封圈提供斜向下压力，使密封环压力分布均匀，将密封环的内壁向与外壁设置泄压槽，并将外壁上的泄压槽和内壁上的泄压槽交错设置。详细方案如图3所示。

2.3 解决密封圈启动稳定性问题

将密封圈的轴向两个端面分别设有多个所述泄油槽，且两个所述端面的多个所述泄油槽交错设置。通过增加泄油槽来实现启动时运行平稳、无滑动，方案详情见图4所示。

3 方案验证

3.1 橡胶密封圈工作原理解释说明

当介质工作空间存在压力的时候，旋转密封与刚性件接触面上必须要有足够大的接触压力，保证接触压力大于介质压力，才能通过该压力作用来阻挡介质泄漏。

因此橡胶圈工作原理是橡胶圈与橡胶密封圈的内外径方向的刚性壁及自身密封接触的接触压力均大于介质压力值，其公式如式（1）所示。

min（P1，P2，P3）≥P                                            （1）

式中：P为介质压力，单位是MPa； P1 为外径及刚性件接触面压力，单位是MPa；P2为外径及刚性件接触面压力，单位是MPa；P3 为组件自身接触面压力，单位是MPa。

发生泄漏在各个方向接触压力的最低值都大于介质压力时才能实现密封，否则就会密封失效。

3.2 橡胶材料超弹理论

O型密封圈常用的是丁晴橡胶材料，O型密封圈在非线性参数中的定量表述是很困难的，所以就需要采用行业通用的超弹性材料变形的本构关系理论来描述材料的应变能密度，进而合理地体现超弹性体非线性的定量表现。

Mooney-Rivlin分析模型是在工程中用于橡胶材料分析常用的模型。在其模型中，其中的应变能密度公式如式（2）、式（3）、式（4）所示：

（2）

（3）

（4）

式中：N为橡胶应变能密度，单位是MPa； T1，T2 为Green应变不变量，常量；Cij 为Rivlin系数，常量。

通过分析，为简化后续计算，将此模型简化到一个参数来描述，则模型式如式（5）所示：

N=C10（T1－3）                                                     （5）

根据资料信息，将此模型简化为两个相关练得mooney-Rivlin 系数参数来描述[3]，如式（6）所示：

N=C10（T1－3）+C01（T2－3）                          （6）

式中：C10，C01为正定常数，统称为 mooney-Rivlin 模型系数。通过这两个参数来描述的模型使用的应变变化范围，这两个变形系数可适应的应变范围达到1.5倍。

3.3 橡胶材料计算模型

橡胶材料模型选用 Mooney-Rivlin 模型，其中C10，C01数值由公式（7）、式（8）、式（9）得到。

lgE =0.0198Y－0.5432                                            （7）

E=6（C10+C01）                                                        （8）

C01/C10=0.01                                                          （9）

式中： Y为橡胶硬度值，单位是HA； E为橡胶弹性模量，单位是MPa。

因此在给定材料硬度值，就能确定计算出其橡胶弹性模量E， Mooney-Rivlin 模型系数C10/C01的比值。根据橡胶材料硬度不同取值，IRHD硬度为40时取0.1，IRHD硬度为60时取0.05，IRHD硬度为70时取0.02。比值随材料的硬度增加而降低，本次取在常温下材料硬度值为 76。

根据式（7）、式（8）、式（9）三个公式计算得：

E=9.15 MPa；C10=1.51；C01=0.0151。

经试验，材料试验机测得材料的泊松比v=0.46。

3.4 旋转密封圈有限元分析数据计算

3.4.1 有限元模型建立

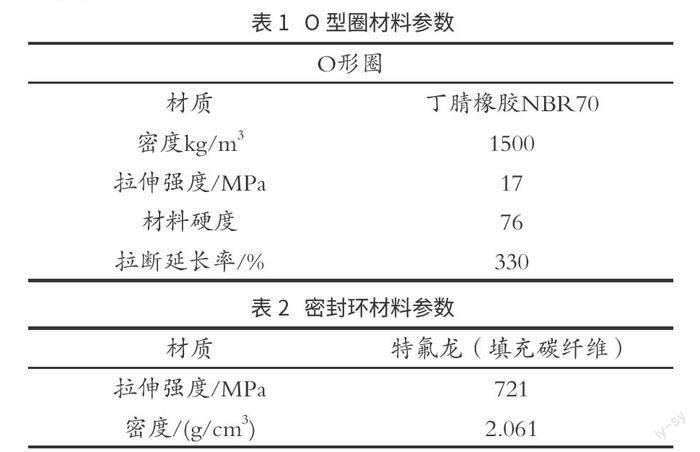
通过designmodel模块进行模型建立，在AnsysWorkbench中建立单侧偏载3 MPa，介质为水，采用 Mooney-Rivlin 非线性应变能量密度本构模型。在径向方向对其力学行为进行数值模拟，通过正交试验，研究不同截面形状O型圈在相同作业环境中的变形、Von Mises 应力和密封面最大接触压力的影响，来进行分析截面形状参数与密封性能的关系，研究选取以250 mm×265.5 mm×6.3 mm型格莱圈为例进行方案验证，并建立了径向位移受限的格莱圈有限元分析模型[4-5]。O型圈材料参数，见表1。密封环材料参数，见表2。约束及载荷条件，见表3。沟槽参数，见表4。隔套42CrMo材料参数如下，见表5。

3.4.2 旋转密封圈的加载方式及边界条件

旋转密封圈的加载数值模拟主要分成两个载荷步来完成。

第一载荷步是模拟格莱圈的初始安装时（O型圈压缩自适应，密封环抱死隔套）。

第二载荷步是单侧3 MPa介质压力对旋转密封圈的侧向单边压缩过程，来模拟旋转密封圈工作时（27 ～ 54 r/min）的实际负载。

3.4.3 接触定义

建立刚性件与O型圈外径的面接触，建立O型圈内径与密封环之间的摩擦接触。同时建立密封环与隔套之间的面接触，接触关系不同时，其摩擦情况也不同，为保证收敛增加摩擦系数为0.2。

4 结语

相同转速及相同偏载时，圆形截面接触压力偏差绝对值为10 MPa，数据稳定性差，在相同水压情况下，侧偏影响较大，磨损加剧。

方形截面接触压力偏差绝对值为3.744 MPa，数据稳定性优。在相同水压情况下，侧偏影响较小，运行稳定。

参考文献

[1] 张翠彬.橡胶O型圈的材料选择分析[J].中国设备工程，2017 （21）：155-157.

[2] 张成富.O形密封圈的压缩率计算方法及实例验证[J].中国石油和化工标准与质量，2018（10）：175-180.

[3] 邓向彬，黄乐，向宇，等.橡胶O形圈最大接触压力、IRHD硬度和压缩率之间的函数关系研究[J].橡胶科技，2019，17（3）： 132-135.

[4] 郭丽霞，关静岩.O型橡胶圈动密封结构的有限元分析[J].科技与创新，2015（3）：19-20.

[5] 赵敏敏.基于Ansys的O形圈橡胶密封圈密封性能及可靠性研究[J].橡胶工业，2020（2）：131-134.