单舰双声呐对鱼雷交叉定位误差分析

肖明恺，张 虹

（中国人民解放军91439 部队，辽宁 大连 116041）

0 引言

水面舰艇的鱼雷防御系统能否有效发挥作战能力，必须依赖于可靠的鱼雷报警信息。在鱼雷预警系统中，尽管对目标的检测、分类和定位都提出了技战术要求，但是目前大中型水面舰艇装备的鱼雷报警声呐仅有被动工作方式，仅能探测到来袭鱼雷的方位信息而无法获取其位置信息[1]，进而无法更为有效地指导对抗器材实施。如果没有相当精度的鱼雷目标距离、位置、状态信息作参照，各型对抗器材都难以完全发挥作用[2]。因此，可通过多声呐系统对鱼雷目标进行联合探测和定位，构建全方位、多层次的鱼雷防御系统，准确获取来袭鱼雷的距离、位置、状态信息，这是提高现有反鱼雷装备器材对抗能力的有效途径[3-5]。

目前，水面舰编队常采用对空队形，间距一般大于30 链，而国内预警探测声呐对于鱼雷目标的探测距离有限，多艘舰艇同时探测到鱼雷信号的可能性较低，所以在防御来袭鱼雷过程中，大多数情况下仍需依靠单舰对鱼雷进行探测定位。随着声呐系统性能提升，舰壳和拖曳式声呐也可以在较远距离上探测到来袭鱼雷方位信息。其中，舰壳声呐一般为由多个水听器组成的大孔径球形或者柱形基阵，拖曳式声呐一般为由多个水听器组成的线列阵，2 种声呐均具有接近全向的噪声信号被动侦测能力。因此，利用单舰舰壳声呐与拖曳式声呐获取鱼雷的方位信息，对来袭鱼雷进行远距离的联合探测和定位，能够快速地获取来袭鱼雷的位置信息，有望大大提高水面舰艇对抗来袭鱼雷的效果。

文献[6]–[7]中对T-R 型双基地声呐系统（T 为发射站，R 为接收站）定位算法精度进行了研究，即通过发射站发出声波经目标散射后到达接收站得到声传播时长，融合方位信息进而确定目标位置，而对于鱼雷这类高速运动目标来说，双程的声传播导致路径变长、声呐发射站无法长时间不间断工作等因素限制了系统探测鱼雷这种突发性且定位实时性要求高的目标。国内也有学者对双基地被动声呐系统对目标定位方法进行了分析，文献[8]利用最小二乘法对目标被动交叉定位存在的误差进行处理，但是需要至少3 部以上的声呐的测量方位信息，这对于实际应用来说难度较大，且在单舰条件下更是无法实现的。文献[9]基于双平台声呐被动工作方式下对鱼雷交叉定位进行了研究，仿真分析了算法对定位误差的影响因素。本文以单舰双声呐被动测向交叉定位技术为基础，首先考察了常规交叉定位算法对目标定位精度的误差分布情况，进而提出基于测量方位滤波的交叉定位算法，并建立典型场景下的动态仿真模型，考察了算法在不同定位误差下的收敛概率。

1 双声呐测向交叉定位原理

双声呐被动探测目标的原理[9-10]如图1所示。声呐与鱼雷目标的距离分别为R1、R2，声呐测量方位角分别为θ1、θ2，2 个声呐距离为L。

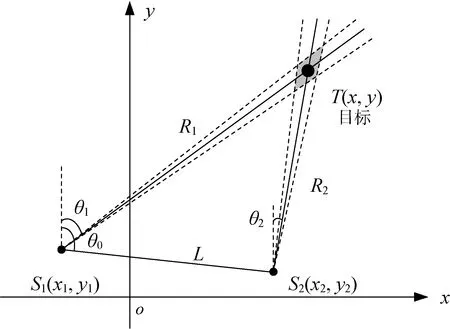
图1 交叉定位原理图Fig.1 Schematic diagram of cross-location

根据正弦定理可得

以S1点为基准，可以求得目标点位置坐标为

假设测量方位误差服从零均值高斯分布，且相互独立，则目标定位误差σx和σy分别为

将各变量的一阶偏导带入式（3），可得定位误差分布情况。根据式（3）可知：定位误差与声呐测量方位误差σθ和基线误差σL有关。本文就以上2 类误差对定位误差的影响进行仿真分析。

2 静态定位误差分析

2.1 测量方位误差对定位误差影响分析

首先，仅考虑声呐测量方位误差对定位误差的影响。仿真参数设置：2 部声呐分别位于S1（–L/2，0）和S2（L/2，0）。其中，基线长度为2 部声呐的声学中心的距离，当前主战水面舰艇长度约为100～200 m，拖曳式声呐缆长的设置主要与所在海域水深以及探测目标深度有关，一般约为 400～800 m，因此本文分别设置L为600 m、800 m、1 000 m。声呐测量方位误差σθ1、σθ2均为4°，仿真结果如图2–4 所示。

图2 交叉定位绝对误差（基线600 m）Fig.2 Absolute error of cross-location（baseline length is 600 m）

图4 交叉定位绝对误差（基线1 000 m）Fig.4 Absolute error of cross-location（baseline length is 1 000 m）

结合静态误差分布情况，在不同基线长度下，在距离原点5 km 和2.5 km 这2 个典型的距离上，统计与基线夹角大于30°范围的误差分布（一般认为夹角小于30°范围内为声呐弱探测区），统计结果见表1。

表1 单舰双声呐交叉定位在典型距离上的误差分布Table 1 Error distribution of cross-location of single-vessel dual sonar at typical ranges

2.2 平台位置误差对定位误差影响分析

考虑平台自身的定位误差，假设的x1和y1测量误差为σx1和σy2，则式（3）改写为

基线长度L设置为1 000 m，声呐测量方位误差σθ1、σθ2均为4°。分别考虑σL、σx1和σy1的影响。首先仅考虑σL的影响，假设σL=50 m，得到的仿真结果如图5所示。

图5 交叉定位绝对误差（考虑基线误差）Fig.5 Absolute error of cross-location（considering baseline error）

再考虑平台自身定位误差的影响，假设σx1=σy1=50 m，得到的仿真结果如图6所示。

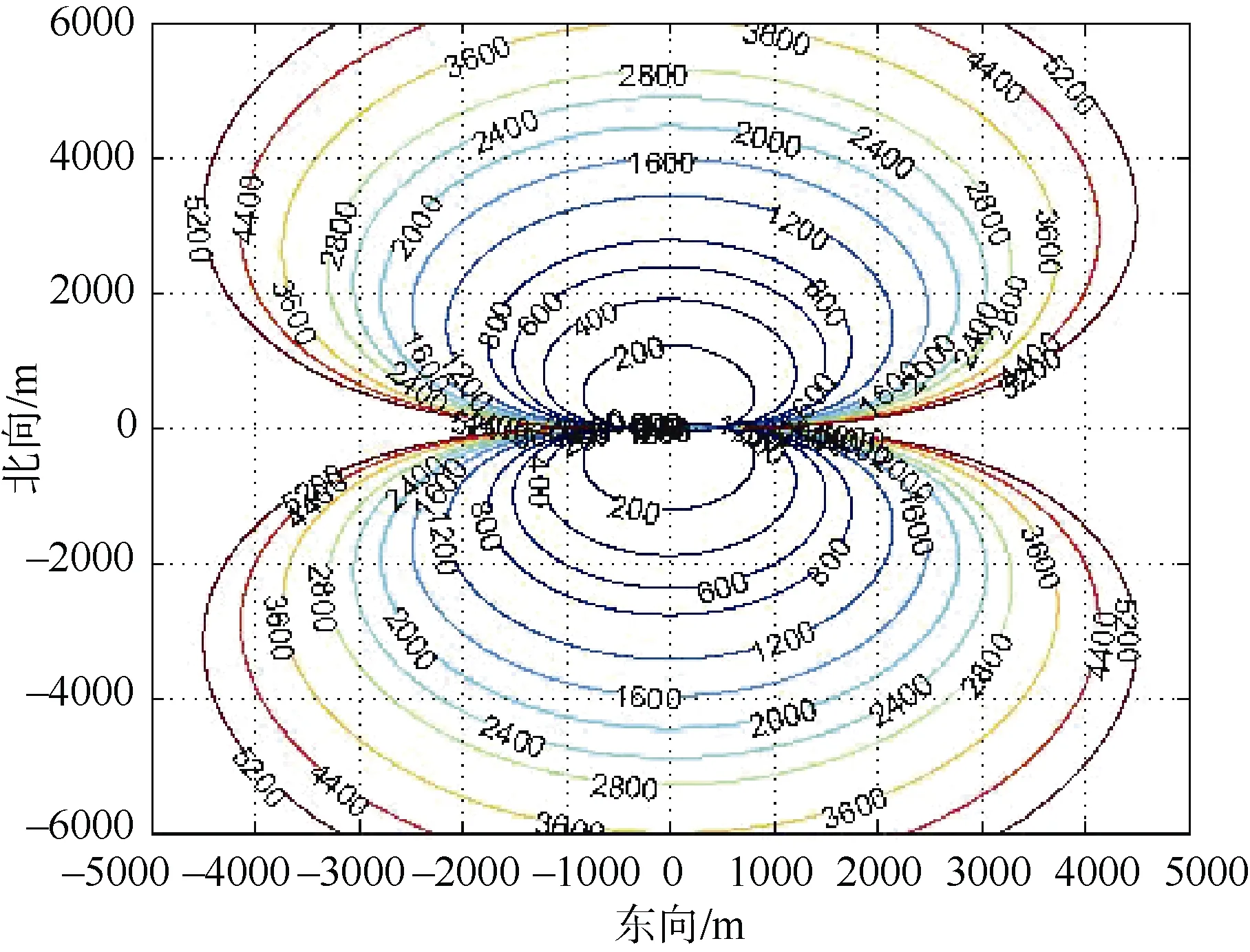
图6 交叉定位绝对误差（考虑平台误差）Fig.6 Absolute error of cross-location（considering platform error）

2.3 小结

从图2–6 中可以看出，目标定位误差主要来自于测量方位误差，而基线误差和平台位置误差对定位误差的影响相对较小，基本不影响定位误差数值和定位误差分布规律。另外，基线长度越长，定位误差越小。因此，在固定基线长度的条件下，应重点优化测量方位误差，以提高定位精度。

声呐方位测量值的误差是随时间平稳变化的，虽然测角误差较大，但方位测量值随时间的变化趋势以及方位测量误差随时间变化的统计平稳性都是有规律可循的，因此对其数据处理时会更为有效；而如果考虑直接优化交叉定位解算之后的定位结果，则会面临定位误差随距离变化导致定位误差非高斯平稳的问题（定位误差大小正相关于距离值）；而使用非线性滤波算法直接通过角度信息解算位置信息，不仅存在定位误差非平稳的问题，还存在非线性解算引入的误差，即使耗费较大的计算量，也难以取得良好的效果。

3 递推平均滤波

递推平均滤波也被称为移动平均滤波或线性平滑滤波，其原理是通过设定一个固定窗长（通常为奇数）的移动滤波窗口，计算该窗口内的数据均值。由于交叉定位误差主要来自于测量方位误差，而测量方位信息是一个相对缓慢变化的量，且不存在较多或连续的突变或野值，因此该方法能有效地消除测量方位信息中的随机波动，具有较高的适用性。递推平均滤波算法计算量小，只需要根据设定的窗长将历史观测数据逐项移动，便可依次计算序列均值，从而用来反映数据长期的变化趋势，同时也具有很好的实时性。

假设输入序列为s(t),t=1,2,…,N，滤波窗长为M，则滤波后输出序列为

由式（5）可知，递推平均滤波器的窗长越长，则选取的数据越多，数据平滑的效果越好。但是，窗长的选择不宜过长，加大窗长会使估计值过多依赖于历史数据，导致其对实时观测数据的变化更不敏感。为解决此问题，改进选用加权递推滤波算法，即对M个观测数据分别设定权值求得输出，即越靠近当前观测数据设定的权值越高：

将测量方位进行滤波后，再进行交叉定位即可得到目标位置信息。

4 典型动态场景仿真及误差分析

为了进一步分析定位精度的影响规律，同时考察基于测量方位滤波的交叉定位算法的收敛概率，建立动态仿真场景。一般情况下，为保持拖曳式声呐在水中良好姿态同时减小噪声干扰以达到良好探测效果，水面舰保持航行速度为8～12 kn。本文重点研究鱼雷直航段，假设鱼雷来袭为匀速直线运动模型，建立以下2 种动态仿真场景。

场景1：设2 个声呐初始位置为S1（–300，0）和S2（300，0），水面舰以10 kn 的速度自西向东航行，声呐测量方位误差均为4°；鱼雷设定9 种典型航迹，航迹的起点距离原点5.5 km，终点距离原点1 km，航速50 kn，方位（鱼雷与基线法线顺时针方向的夹角）分别为300°、315°、330°、345°、0°、15°、30°、45°、60°，如图7所示。

图7 动态场景下的典型航迹设置Fig.7 Typical track settings in dynamic scenes

场景2：2 个声呐初始位置坐标设定为S1（–400，0）和S2（400，0），其它参数均相同。

为了分析随机误差对定位精度的影响，对声呐测得的鱼雷方位信息添加噪声（高斯白噪声），以表示系统观测时具有的随机误差。由于噪声的随机性，单次仿真的结果不足以证明算法的真实性能。在同样的条件下，本文进行1 000 次蒙特卡洛仿真试验，统计2 种场景下算法的误差分布情况得到图8和图9。

图8 常规交叉定位算法定位误差Fig.8 Positioning error of conventional cross-location algorithm

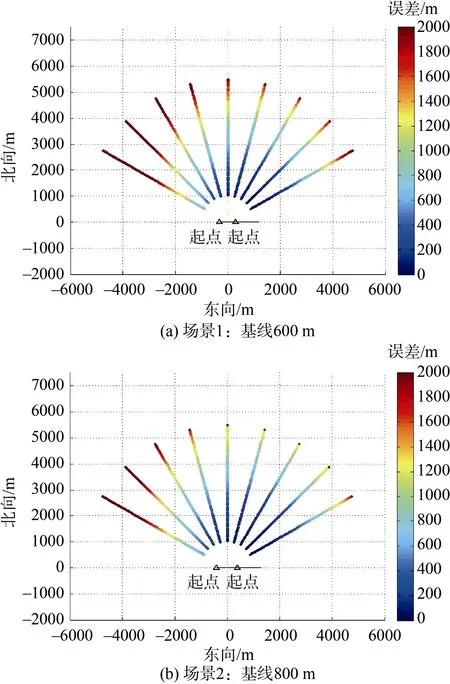
图9 测量方位滤波的交叉定位算法定位误差Fig.9 Positioning error of cross-location algorithm for measuring azimuth filtering

使用圆概率误差描述定位算法在各点的定位精度，即取N次蒙特卡洛试验中定位误差的中位数，用于评价在该点的定位精度[11]。本文在上述仿真场景的基础上，将目标的来袭方向设置为每间隔1°变化1 次，对与基线法线夹角–60°～60°范围内的所有角度都进行1 000 次蒙特卡洛试验，统计算法在不同距离区域内不同定位误差下的收敛概率，统计如表2–3 所示。

表3 测量方位滤波的交叉定位算法误差收敛概率Table 3 Error convergence probability of cross-location algorithm for measuring azimuth filtering

从上述仿真结果中可以看出，测量方位滤波的交叉定位算法明显优于常规交叉定位算法。

5 结束语

本文以双声呐站交叉测向定位原理为基础，仿真分析在典型测量误差下，鱼雷目标定位误差空间分布情况，结果表明：交叉定位算法的定位误差在固定基线条件下主要受测量方位误差影响。基于此，提出了对测量方位滤波的交叉定位算法，建立了动态仿真模型考察算法性能，结果表明：该算法具有更高的定位精度和收敛概率。该研究结论可为利用单舰双声呐系统进行鱼雷目标交叉定位提供依据。