近水面有限长谐振动圆柱的远场声学模型研究

聂 睿，李孟捷，辛子豪，高晟馨

（1.中国船舶集团有限公司第七一〇研究所，湖北 宜昌 443003；2.清江创新中心，湖北 武汉 430076）

0 引言

与经典无限域场景不同，受近处水面影响，由有限长圆柱壳表面振动产生的辐射声波传播至水面后，将在水面处发生反射；反射声波传播至柱壳结构时，声波又将在结构表面发生刚性散射，部分散射声波又会传播到水面处形成新的反射声波，如此周而复始，经多次结构表面散射与多次水面反射后，这些声波将最终构成（准）稳态声场。部分学者将反射定义为一种特殊散射，故需考虑结构与水面相互影响的声学问题也被称为互散射问题[1]。

由于结构表面的辐射声波与散射声波都能以相似数学表达式进行描述，因此大多数学者会先将其置于同一声波式下，并不进行细分。对于水面反射作用，则可基于镜像原理，假定存在一个对称的虚源，水面处反射波可视为以该虚源为声源产生的（虚）辐射声波；由此，整个声场内所有声波都可以归为2 大类，实源声和虚源声（模型一）。基于该模型建模思路，HUANG[2-3]分别针对球壳和二维柱壳结构，建立其半空间声场计算模型，分析研究平面入射波激励下整个系统的散射声场特点。HASHEMINEJAD[4-5]则针对谐振动二维圆柱的辐射声问题，对空间限制造成的声场变化开展了详细研究。AVITAL[6]利用该建模思路，以半空间球壳为例，通过施加分布载荷改变结构表面振动特性，进而控制系统声场分布，实现振动噪声的主动控制。

与模型一类似，边界元方法常用于半空间声学分析，其处理声场边界的基本思路亦是通过镜像原理引入虚源，对三维声学Helmholtz 方程基本解进行叠加修正，由此可进行考虑声学边界影响的耦合系统振动或声学性能分析研究[7-8]。邹元杰[9-10]将结构有限元与声学边界元进行结合，得到数值计算分析模型，对自由液面和刚性壁面两类工程常见环境因素造成水下方箱结构振动特性的变化进行了分析研究。然而，由于边界元方法与模型一研究思路相同，即把辐射和散射统一为一类声，因此也只能计算声学总量。

将声波类型与声波来源结合，有关学者进一步提出了4 类声波的细分方法，即实源（振动结构）弹性辐射声、刚性散射声与虚源（自由液面）弹性辐射声、刚性散射声，这样的分类方式有利于针对散射声或辐射声以分析其各自声场形式特点。白振国[11]建立了考虑自由液面影响的有限水深二维圆柱壳振动声学耦合模型，其声学部分基于以上细分方法开展了计算分析，由此明确了刚性散射声的影响，并给出了潜深对各类声波的声场分布与传播衰减特性的影响规律。在该模型的基础上，针对结构间相互影响作用，张林根[12]建立了有限水深双二维圆柱壳声场计算模型，重点分析研究了壳体间的相互影响，即结构声遮挡问题。

目前对半空间圆柱结构的声学解析研究工作主要集中于二维问题，相比于二维圆柱模型，有限轴向长度会造成声场求解难度增大。而且对自由液面与结构表面互散射具体过程研究也较为稀少，即缺乏对每次散射及其反射声的量化分析研究。因此，本文建立了半空间有限长谐振动圆柱多次散射声场模型（模型二），定量研究了散射声随散射次数的变化规律，以及浸没深度、频率等相关参数对散射声的影响。

尽管2 种模型数学机理是一样的，但相比于模型一、模型二能够区分辐射和散射的成分，可对每次散射及其反射声进行定量研究。本文一方面对2 类模型开展辨析研究，着重分析不同参数下，如不同浸没深度时，散射效应的强弱；另一方面开展定量计算研究，获得了散射声随散射次数的衰减变化规律，对深入研究近水面互散射机理有重要意义。

1 理论分析

本文研究针对的振声耦合系统如图1所示。其中，圆柱壳结构的长度为L，截面半径为R；壳体中心线与自由液面平行，两者之间的距离即为壳体浸没深度，为H。将柱壳结构正中心点定义为所有坐标系的原点O，全局坐标系为标准左手坐标系O–（x，y，z）；壳体及声场则在柱坐标系O–（x，r，φ）下进行描述，x方向为壳体轴向，r方向为壳体径向，φ为周向角（r向与y轴的夹角）。远场声压观测点为P点，其空间位置则由球坐标（R0，θ，φ）进行描述，R0为P点与坐标原点O间的距离，θ为观测角（向量OP与x轴的夹角）。

图1 耦合系统示意图Fig.1 Schematic diagram of coupling system

如前文所述，自由液面可基于镜像原理通过引入虚源进行模拟，其产生的所有反射声都可以由虚源发出的（虚）辐射声进行等效。虚源坐标系原点O′与原点O关于自由液面对称，其坐标系为O′–（x′，r′，φ′），如图2所示。

图2 自由液面虚源处理示意图Fig.2 Schematic diagram of free surface virtual source treatment

本文进行声压计算时，需将流域在壳体两端进行截断，并假设两端处存在2 个无限长声障柱。由此将引入新的壁面连续条件，即声障柱表面处声压速度为0。此外，出于计算过程简化的考虑，本文将先采用傅里叶变换方法，将声压由实际坐标系轴向x表达转换到波数域下，进行有关计算后，再由傅里叶逆变换确定最终声压表达式。声压傅里叶变换及逆变换具体表达式如下：

1.1 模型一建模流程

构建模型一时，声场声压可统一划分为实源声压Pr与虚源声压Pi2 大类。对于虚源声压Pi，根据分离变量法，可将其进一步分解为[1]

声压Helmholtz 方程在波数域下的表达形式如下：

能满足上式的声压存在特定形式解，通常将其称为傅氏声压，则实源傅氏声压如下：

与之类似，虚源发出的傅氏声压具体表达如下：

当声波由水下向空气传播时，由于空气波阻抗远小手水下波阻抗，因此两者交界面自由液面可以近似定义为绝对软边界，该界面上的声压恒定为0。那么，自由液面上任意一点（r=r′，φ=π-φ′），其声压为实源声压与虚源声压之和，应满足进一步可推导出下式：

根据柱贝塞尔函数的Graf 加法原理[13]可实现坐标迁移：

式中：Jn（）为第n阶第一类贝塞尔函数。

对于谐振动圆柱壳，其径向位移可表示为如下形式：

为便于后续计算，同样要将结构径向位移变换到波数域，其形式变为

结构与声场需满足流固交界面处速度连续条件，其在波数域下的表达式为

式中，ρf为流体密度。

为便于进行计算，上式所有量都应在同一坐标系下进行表达，因此将虚源傅氏声压转化到实源声压的坐标系下，因为r=R<2H，有：

交换积分顺序后：

将式（12）代入式（10）后，级数做有限截断，均从–N取到N，可以得到波数域声压幅值向量与位移幅值向量的关系：

式中：[Tran]矩阵为波数域中幅值迁移矩阵；

完成波数域下有关计算后，进行傅里叶逆变换即可获得任意场点声压：

对于远场声压，可以采用稳相法[14]求解，限于篇幅，本文直接给出球坐标系下声压表达式[15]：

式中，｛An(kfcosθ)｝可由式（13）求得。

1.2 模型二建模流程

构建模型二时，柱壳结构由振动会产生实源弹性辐射声压Per，该声压传播到水面时，产生虚源弹性辐射声压Pei；随后，反射声压传播到结构处时，产生实源第1 次刚性散射声压，该散射声压又会产生虚源第1 次刚性散射声压；如此周而复始，最后形成实源第K次刚性散射声压、虚源第K次刚性散射声压[16-17]。

实源弹性辐射声可直接由速度连续条件求出，方程如下：

第1 次实源刚性散射声由虚源辐射声引起，结构表面处：

第2 次实源刚性散射声由第1 次虚源刚性散射声引起，类似有：

依次类推，第K次实源刚性散射声由第K–1次虚源刚性散射声引起：

根据上述条件，可以求出每一次散射及其反射声的波数域幅值，同理可由稳相法求出各成分声压。

2 数值计算

本文研究计算模型有关参数如下：圆柱壳长度L=1 m，截面半径R=0.2 m，外部声场介质密度ρf=1 025 kg/m3，介质声速cf=1 500 m/s。

2.1 准确性验证

使用边界元方法建立计算模型进行声学分析是目前主流工作思路。因此，本文通过对比本文模型一与边界元方法（BEM）的计算结果来验证理论计算方法准确性。

本文研究中，圆柱壳结构表面为谐振动，振动法向速度幅值假定为10–6m/s 不变。开展准确性验证时，分别以浸没深度H=4R、频率f=100 Hz和浸没深度H=2R、频率f=1 000 Hz 2 种工况进行计算说明。声场观测点P有关参数为：观测半径R0=1 000 m，观测角θ=π/4，周向角φ取–π/2～π/2。定义声压级SPL=20log10（|P|/P0），单位dB，其中|P|为声压压强绝对值，基准声压P0=10–6Pa。由此，可计算得到2 类方法下声压指向图如图3所示。

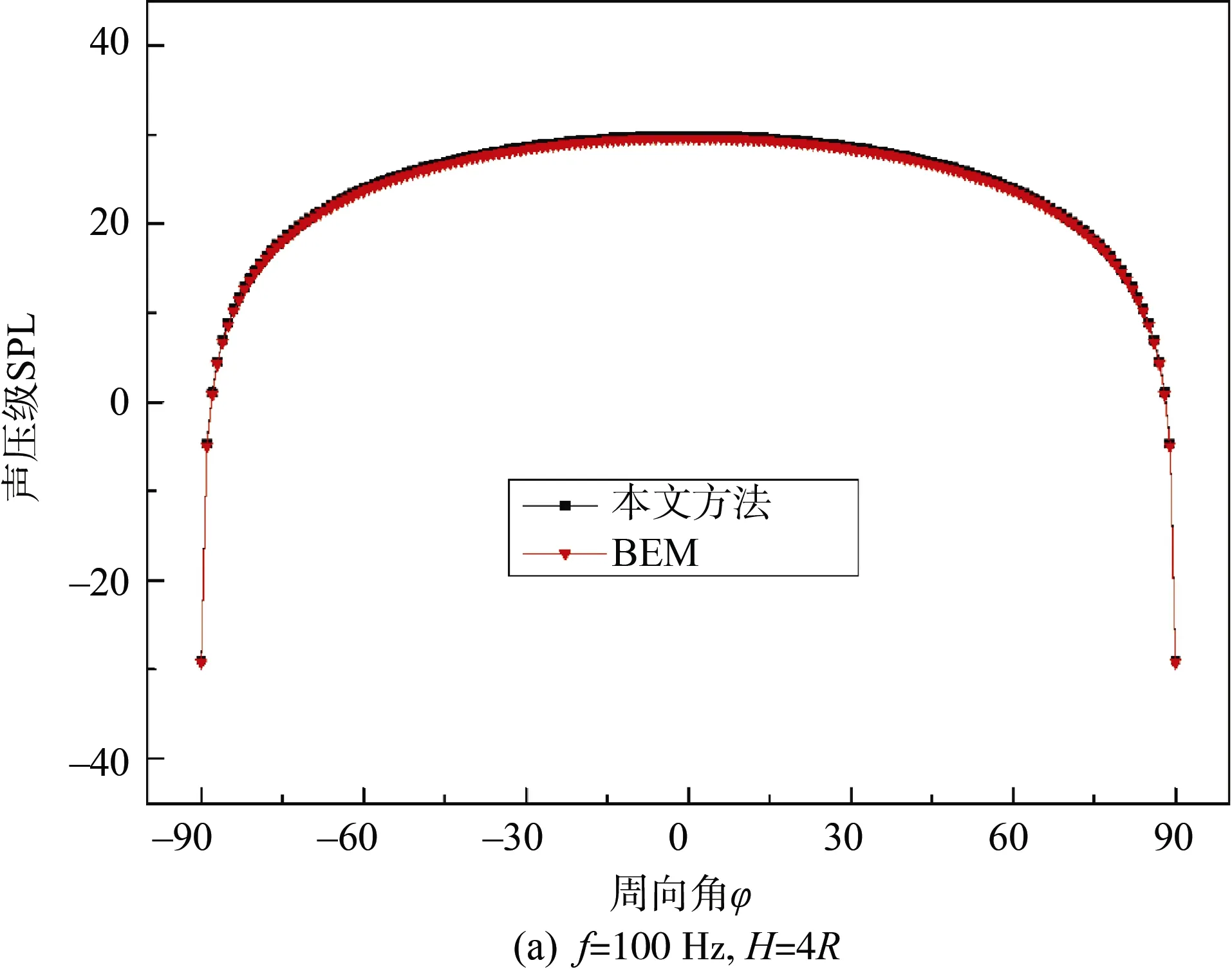
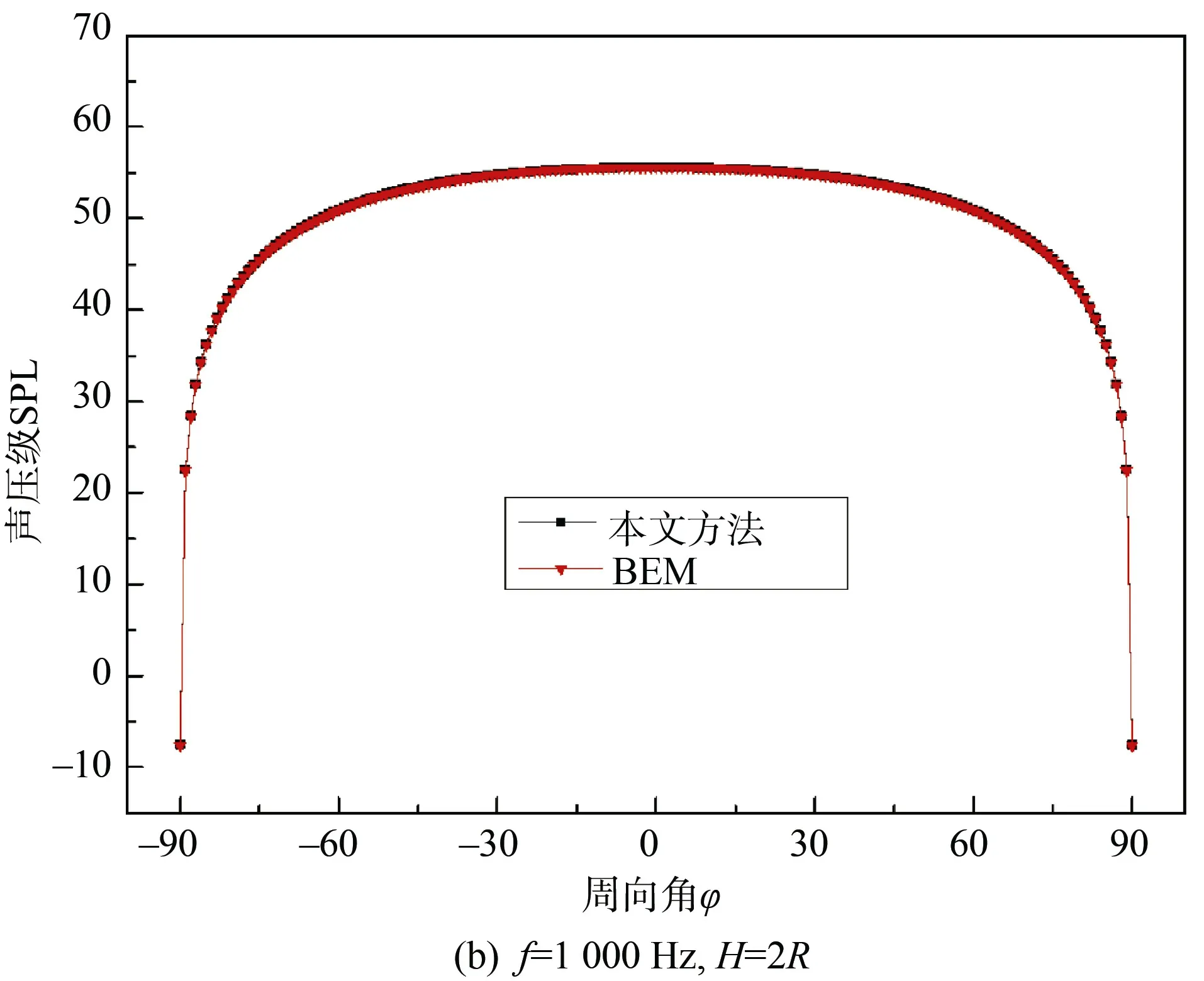
图3 本文方法和BEM 计算结果对比Fig.3 Comparison of calculation results of the proposed method and that of BEM

由图3可以看出，两类方法计算获得声压指向性曲线在不同工况下都吻合良好，证明本文理论计算方法准确可靠。

2.2 两类模型统一性分析

两类模型数学本质是一样的。从公式推导可以看出，2 类模型建立过程中，声压的弹性辐射声与刚性散射声拆分与否并不影响流固交界面和自由液面处声场额外约束的表达。模型二与模型一相比，仅仅是加强了刚性声的细化拆分，各声波之间的物理联系与数学表达没有变化。

下面以浸没深度H=2R、表面振动频率f=100 Hz和浸没深度H=4R、表面振动频率f=1 000 Hz 2 种工况为例，分别用2 类模型计算声场观测点（1 000，π/2，0）处的总声压，且模型二取不同散射次数进行计算，结果如表1所示。（其中K表示上文提及的散射次数，K=4 表示叠加到第4 次散射声及其反射声）

表1 两类模型总声压级Table 1 Total sound pressure level of two kinds of models

从表1可以看出，模型二总声压级与叠加的散射声次数相关，当K取到4 时总声压级基本与模型一相同，计算结果可充分证明两类模型的统一性。

2.3 浸没深度影响

对于给定的结构尺寸以及速度分布形式，声场某处各类声波的强弱程度取决于浸没深度以及频率的大小。采用模型二可以详细分析此类问题。将实源散射声和其反射声之和定义为总散射声Ps，将实源辐射声和其反射声之和定义为总辐射声Pe，总声Pt=Pe+Ps。

场点坐标、模型参数和壳体振速与2.2 小节完全相同。为使计算结果不受模型尺度影响，故将频率和浸没深度均无量纲化，定义无量纲频率为kfR，无量纲浸没深度为H/R。分别取频率kfR=0.1 和1，H/R从1 取到10，绘制总散射声Ps、总辐射声Pe、总声Pt声压级曲线。

由图4可以看出，kfR=0.1 时，散射声压级在浸没深度为4 倍半径时与总声压级相差约28 dB，此后逐步增大，散射声在浸没深度大于4 倍半径后几乎可以忽略，辐射声和总声曲线基本重合。kfR=1时，散射声波和辐射声波都呈周期波动，但二者存在相位差，辐射声压级整体上比散射声压级约大10 dB；但在辐射声压谷值点附近区域，散射声压级反而会大于辐射声压级。

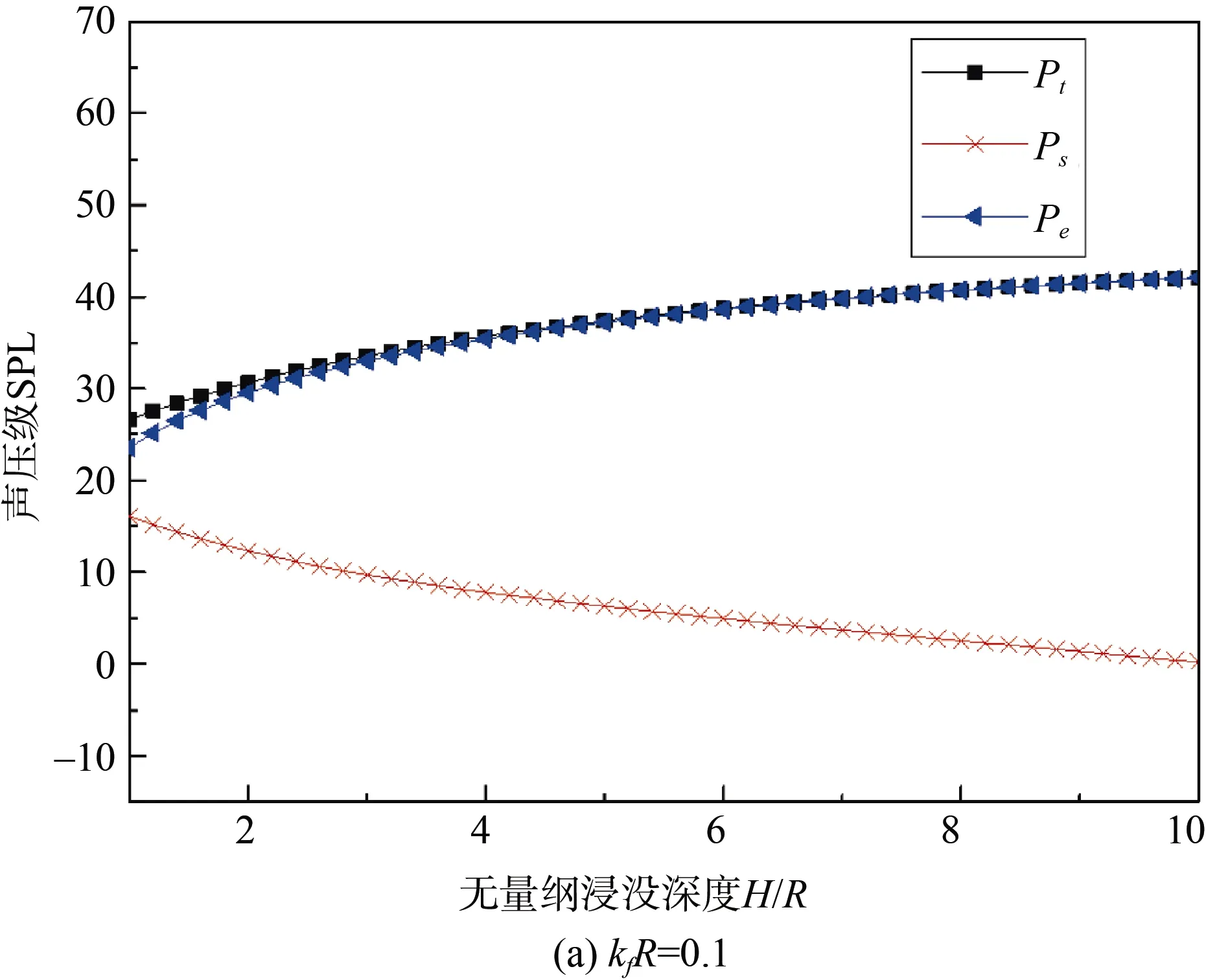
图4 散射声、辐射声、总声随浸没深度变化曲线Fig.4 Scattered sound，radiated sound，and total sound curves with immersion depth change

以上现象的出现是由于自由液面的存在，使声波与其反射声发生干涉，出现了类偶极子效应[18-19]。在场点（1 000，π/2，0）处，由于距结构的距离足够远，此问题可简化为点源问题进行分析[20]。虚、实源可视为波程差为2H的2 个独立点源。由于声压的周期性，若波程差变化量为声波波长整数倍时（kf△H为π 的整数倍），声压大小将保持不变，故声压随浸没深度增大呈周期变化。此外，当频率比较小时，浸没深度到较大的值时该波动规律才可能出现。

2.4 散射声衰减规律

从表1可以发现，散射声强度随散射次数增大出现了衰减。对该规律进一步探究，有利于深入了解近水面互散射机理。下面，利用本文模型二，计算相关声学量，进行定量分析。

辐射声Pe的定义保持不变，第1 次刚性散射声及其反射声定义为Ps（1），第2 次散射声及其反射声为Ps（2），第K次散射声及其反射声为Ps（K）。进行有关计算时，大部分参数仍然不变，但观测点观测角取θ=π/4，周向角φ取–π/2～π/2。无量纲频率可取kfR=0.1 或1，无量纲浸没深度可取H/R=2或4，两者组合后可定义4 组工况，各工况下辐射声压级和每次散射声压级指向性曲线如图5（最大散射次数取到4）。

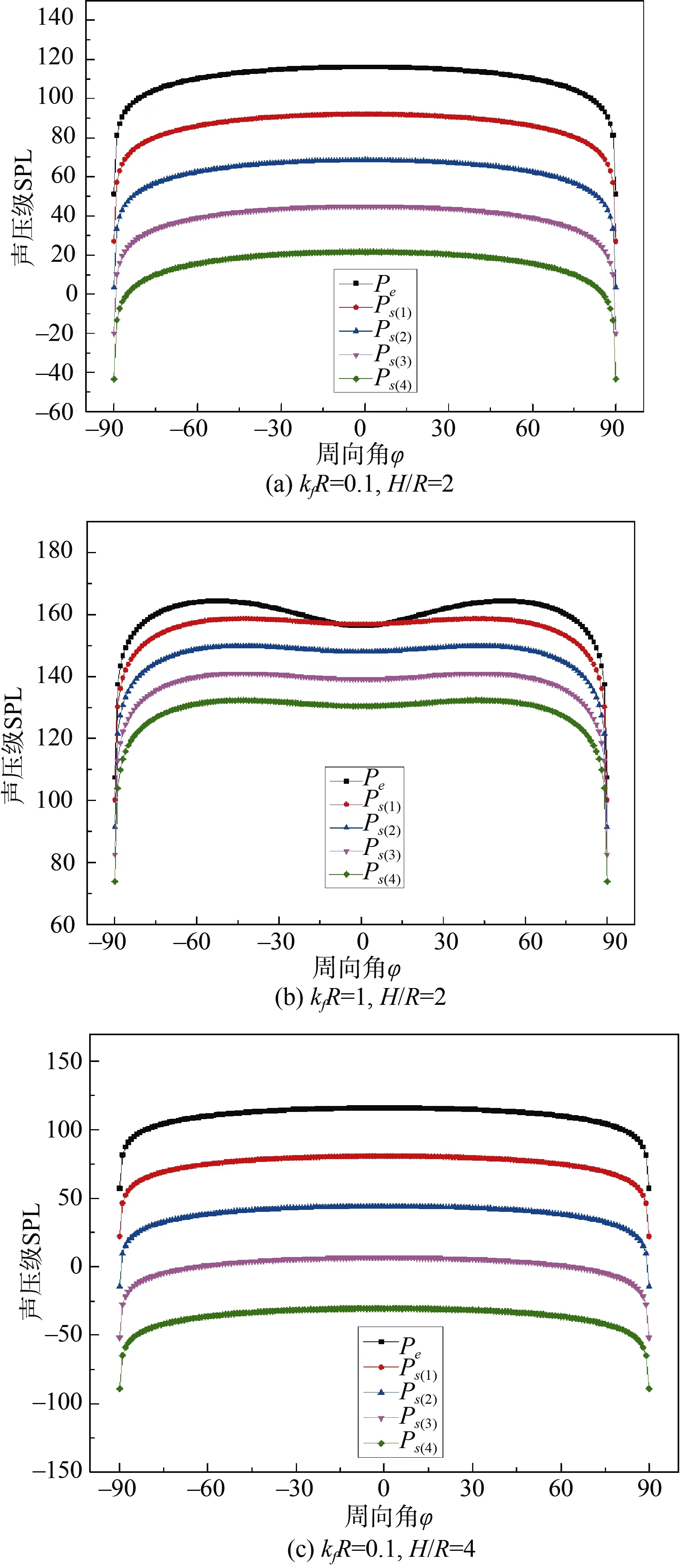
图5 散射声衰减规律Fig.5 Attenuation law of scattered sound

由图5可以看出，一方面，由于类偶极子效应，辐射声在频率较高时或者浸没深度较大时出现指向性的分瓣；散射声亦有类似性质，但指向性曲线更平缓。另一方面，散射声随散射次数衰减的分贝值几乎恒定，或者说，散射声随次数按固定倍数衰减。具体来说，相同频率下，随着浸没深度增大，散射声衰减越快。以kfR=0.1 为例，H/R=2 时，每次衰减约24 dB；H/R=4 时，每次衰减约37 dB。而当浸没深度不变时，随频率增大，散射声衰减越慢，以H/R=4 为例，kfR=0.1 时，每次衰减约37 dB；kfR=1 时，每次衰减约12 dB。

3 结束语

本文建立了近水面有限长谐振动圆柱2 类数学物理模型，并通过解析方法辨析研究了2 类数学物理模型的异同，并得到如下结论：

1）2 类模型本质上是一致的，可根据关心的声类型选择对应计算模型。比如单纯计算远场点处声压，可选择模型一；如想定量研究辐射声和散射声的传播特点，则选择模型二。

2）自由液面会带来类偶极子效应，即远场给定场点的总辐射声、总散射声和总声均会随浸没深度增大呈周期波动，而且频率越高周期越短，但总辐射声、总散射波动时存在相位差。

3）散射声压大小随次数按一定倍率衰减，而且相同频率下，浸没深度越大，衰减越快；相同浸没深度下，频率越低，衰减越快。因此，在浸没深度很小或者振动频率很高的情况下，散射声衰减很慢，需要很多次散射后其量级才能被忽略，也就是说混响效应比较强烈。