二维透声窗遮挡损失计算方法研究
2023-06-26赖喜悦陈美霞董文凯
赖喜悦,陈美霞,董文凯
(华中科技大学 船舶与海洋工程学院,湖北 武汉 430074)
0 引言
装有声呐设备的舰艇艏部透声窗是水下反潜作战的探测窗口[1]。透声窗内部声呐设备工作时,基阵发射的声波经过导流罩透射到外部声场,由于透声窗的遮挡和导流罩内部结构的透声损失,波束会发生畸变,并伴随着能量损失。因此,透声窗设计在满足结构强度、阻力和耐用性等要求的前提下,还需要着重考虑其声学特性[2]。
因透声窗遮挡作用带来的声波能量损失被定义为遮挡损失,是透声窗声学特性设计关注的重点之一。然而,由于透声窗结构比较复杂且模型尺寸一般较大,加之工程中关注的频率范围并不局限于低频,透声窗遮挡损失的准确计算较为困难。因此,在许多文献中往往通过对平面波入射下单层或多层介质模型的透声性能进行研究计算来粗略预报透声窗的声学性能。LEE 等[3]利用三层和四层介质模型对复合透声窗材料在一定频率下的插入损失进行了理论计算,并开展实验验证了计算结果的准确性。童晖等[4]利用三层介质模型对透声窗材料在高频下的声学特性进行了研究,并探讨了材料属性和平面波入射角度对其插入损失的影响。易燕等[5]提出了一种低频宽带测试技术,解决了双层钛合金导流罩平板模型低频段和大角度测试难度问题,得到了模型试样低频宽带范围内插入损失的频率谱和角度谱。李东升等[6]利用夹芯透声窗的简化模型研究了夹芯透声窗参数对其声学性能的影响,并对比了不同频段下夹芯透声窗与单层玻璃钢透声窗透声性能的差异。此外,李源源[7]等建造了实际舰艇球鼻艏导流罩模型,实验得到了球鼻首的全向和定向发射透声损失。
综上,对透声窗声学性能进行准确预报是对其进行声学设计的前提,而简化的单层或多层介质模型无法考虑实际透声窗的复杂结构、复杂边界和复杂声源,只能粗略地估算透声窗的声学性能。实验方法研究透声窗模型的声学性能又会带来较大的实验成本,因此,提出一种准确预报透声窗遮挡损失的计算方法具有切实意义。
本文提出了一种解析–数值混合方法,用于快速预报透声窗的遮挡损失。首先,利用球谐波展开法得到了单活塞声源的声场分布,并通过叠加原理得到阵列声源的声场分布,进而根据透声窗有限元模型各网格节点的坐标得到模型表面任意一点由声源激励引起的声压和法向振速。将之插值回COMSOL 有限元模型之中,调用 COMSOL 的Kirchhoff-Helmholtz 模块通过再辐射的方法求解模型的遮挡损失,最后建立简单二维透声窗模型,验证了方法的有效性。具体的计算流程如图1所示。
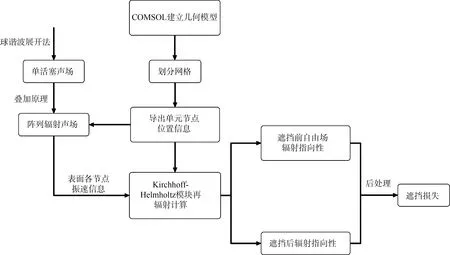
图1 解析–数值混合方法计算流程图Fig.1 Flowchart of the calculation process of analysis-numerical hybrid method
1 活塞阵列声源声场分布
要想对透声窗模型遮挡损失进行准确计算,声源的建模和求解是第一步应该做的内容。圆柱形基阵是目前国内外舰壳声呐最普遍的一种基阵形式,受水面舰吃水深度的限制,通常采用收发合置的声基阵,使得这种基阵形式对水平 360°范围具有相同的探测能力。实际研究中可以将这种基阵简化为圆面活塞阵列,在定向发射时,可以根据相控规则调控各活塞振元的振动相位,使得各个活塞辐射声场波阵面重叠,实现波束聚焦都效果[8]。
1.1 球谐波展开法求解单活塞声场
文献[9]和[10]采用球谐波展开法求解了圆盘形辐射体在声场中的声辐射,对于二维模型来说,阵列的每一个振元都可以简化为以一定振速在自由空间中简谐振动的线段,线段在y>0 方向的法向振速为V0,在y<0 方向的法向振速幅值为–V0,活塞半径为a,r和θ分别为测点半径及其与y轴正方向的夹角,模型示意图如图2所示。

图2 单活塞声场分布示意图Fig.2 Schematic diagram of sound field distribution of single piston
将无限水域划分为子域Ⅰ(0≤r≤a,0≤θ≤π /2)、Ⅱ(0≤r≤a,π /2≤θ≤π)、Ⅲ(r≥a,0≤θ≤π)后,各子域声压满足时间简谐形式如式(1)所示:
式中:ω为振动圆频率;j为虚数单位;μ=1,2,3。
忽略时间项exp(-jωt),各子域声压还应满足如下边界条件:Z0为介质特性阻抗;k为流体中的波数。
从而,各子域的声压函数可以假设为式(3)中的形式:
式中:An,Bn和Cn为未知系数;J和H分别表示一类贝塞尔函数和汉克尔函数,H的下标表示其阶数,上标表示其为第一类汉克尔函数。
各子域之间需要满足的声压–振速连续性条件如下:
将各子域假设的声压函数代入到上述连续性条件中,可以得到式(5):
式(5)的第2、3 个方程左右两边同时乘以cos(mθ),m和n均为自然数,并在两方程θ的取值区间内积分,可以得到式(6):
其中分部积分可求得:
式中,pm(nm,n)=qmn(m,n)=,m=n,且m,n为奇数。
从而可知pmn和qmn有下面的性质,
取m=2s+1,s为自然数,将式(6)中的2 个方程相加,利用上述pmn和qmn的性质可以得到式(9):
式(9)等式两边同时在r=a处对r求导,可以得到式(10):
联立式(9)和式(10),取截断数s=n=N,即可以得到一个由2*(N+1)个方程组成的线性方程组,求解线性方程组,得到声压函数中的未知系数An,Bn和Cn,回代到式(3),即可得到单活塞辐射声场。
1.2 叠加原理求解活塞阵列声源声场分布
多个活塞组成阵列时,阵列半径为Rr,活塞个数为2*Ns+1,即以第Ns+1 个活塞为中心,左右两边各有Ns个活塞,活塞间隔圆心角为δθ,第i个活塞与中心活塞的夹角为φi,阵列发射方向与中心活塞的夹角为θr。为了实现定向发射的功能,不同活塞振动在时域上需要存在一定的时延关系,这种关系可以通过调节频域上的相位差来实现,即不同活塞的速度振幅可以由如下形式表出:
式中,V0i表示第i个活塞的法向振动速度幅值。
忽略活塞之间的相互作用,阵列辐射声场可以看作是单活塞声场叠加而成,从而总声场可以表示为
式中:TR,Tθ表示测点坐标;ri,θi表示测点在第i个活塞局部坐标系下的坐标。如图3所示,对于平面上任意一点(TR,Tθ),我们都可以由余弦定理将其在第i个活塞局部坐标系下的坐标(ri,θi)表示成式(13)的形式:

图3 局部坐标系下测点坐标示意图Fig.3 Schematic diagram of measurement point coordinates in local coordinate system
获取了阵列辐射声场任意一点的声压P(TR,Tθ)后,结合透声窗舱室几何信息,就可以获取透声窗及舱室表面任意一点处的声压与法向振速。
2 透声窗遮挡损失计算
以阵列中心为全局坐标系的原点建立透声窗舱室轮廓模型,对于透声窗舱室表面上任意一点,其坐标向量可以设为=[x,y]T,该点处的外法向单位矢量为=[nx,ny]T,从而该点处由阵列声源激励起的法向振速vn()可以表示为式(14)的形式,式中dΔ 为一较小的值,可取对应频率下流场声波波长的1/20。
依据惠更斯原理,文献[11]提出了一种再辐射的方法来计算透声窗内声呐基阵的远场辐射指向性,这种再辐射的方法很好的适应了实际透声窗内的声场分布情况,运算比较简单。结合这一方法,可以将遮挡损失的计算分为2 步:第一步是计算阵列在自由场中的远场声压级指向性,第二步是计算透声窗遮挡后远场声压级指向性,两者之差即为遮挡损失。
依据图1,获取表面振速信息后,调用有限元软件COMSOL Multiphysics 6.0 的Pressure Acoustics,Kirchhoff-Helmholtz 模块(压力声学,基尔霍夫–亥姆霍兹模块)进行再辐射计算。通过输入振速,该模块基于基尔霍夫–亥姆霍兹积分公式对高频辐射问题进行计算,而无需对周围流体进行建模,可以极大地降低有限元模型的复杂度,使得计算较为迅速。调用Kirchhoff-Helmholtz 模块后,在COMSOL中调用MATLAB 插值函数将振速输入到几何和网格表面,得到再辐射源。计算无遮挡声场源特性时,需要将整个舱室外表面选中,给每个节点插值对应的法向振速,而计算遮挡后的辐射声场时,只需要将透声表面选中并赋予振速计算。最后,只需要在后处理中将2 次计算结果相减,即可得到模型的遮挡损失。
3 方法有效性验证
3.1 单活塞声场有限元验证
在COMSOL 中建立二维单活塞模型,活塞半径为35.5 mm,计算频率为10 kHz,活塞法向速度幅值为1 m/s。有限元模型如图4所示,其中内圆的水平直径即为活塞,内圆和中间圆为水域,水的密度为1 000 kg/m3,水中声速为1 500 m/s,外圆为PML 层。理论与有限元计算得到的该频率下距离圆心r=1 000 m 处一周的声压如图5所示。可以看到两者的计算结果吻合较好,说明球谐波展开法能较准确地求解单活塞在水中的辐射声场。

图4 单活塞有限元模型Fig.4 Finite element model of single piston
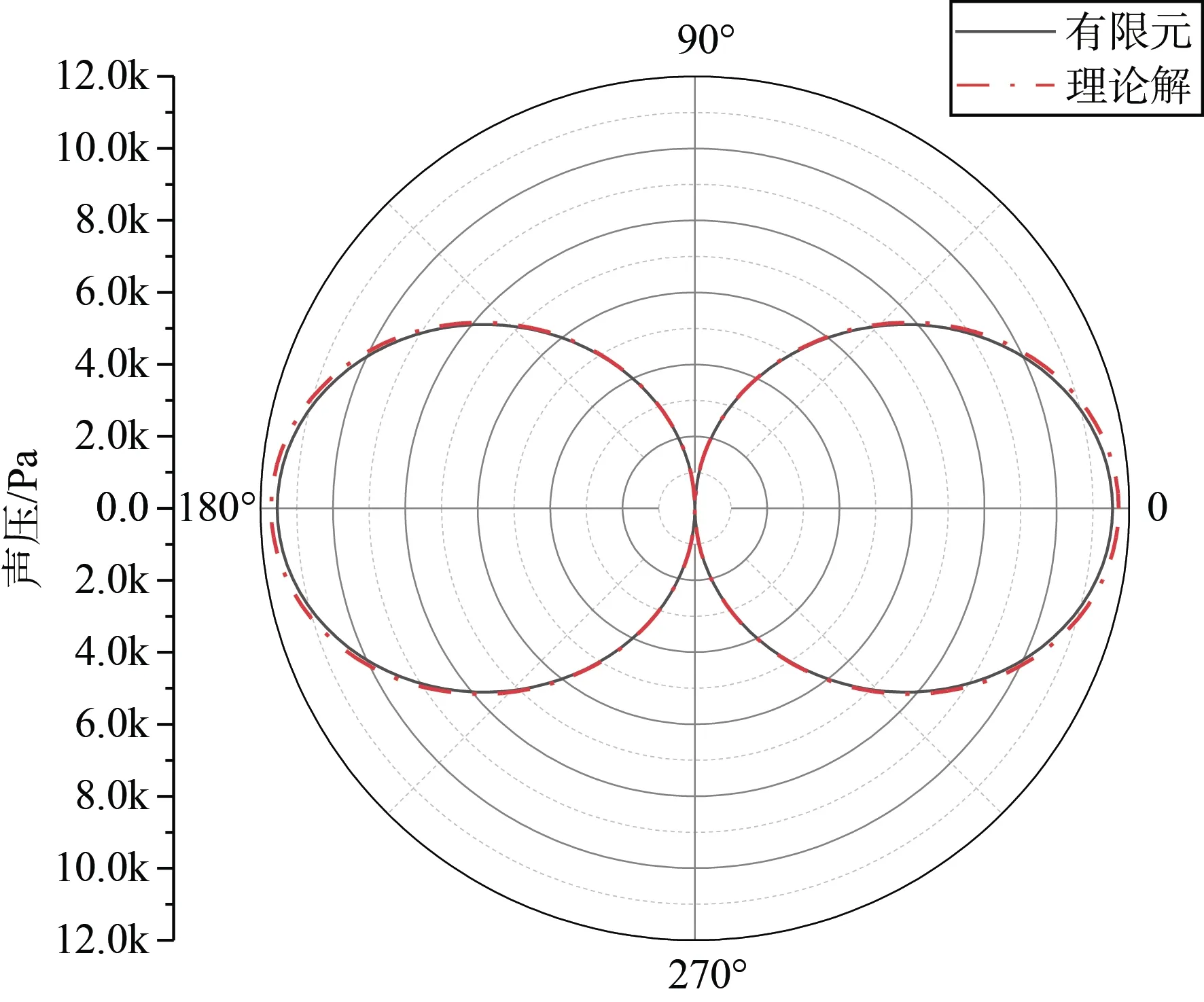
图5 单活塞r=1 000 m 指向性图Fig.5 Directivity pattern of single piston at r=1 000 m
3.2 活塞阵列声源声场有限元验证
在COMSOL 中建立活塞阵列模型,NS=10,各活塞的直径均为35.5 mm,活塞法向速度幅值为1 m/s,阵列半径为1.2 m,活塞间隔圆心角为3.5°,θr=0°,计算频率为10 kHz,有限元模型示意图如图6所示,理论与解析计算得到的该频率下距离圆心r=1 000 m 处一周的声压如图7所示。也可以看到理论结果能与有限元结果吻合较好,阵列定向发射时,能量主要集中在发射方向。
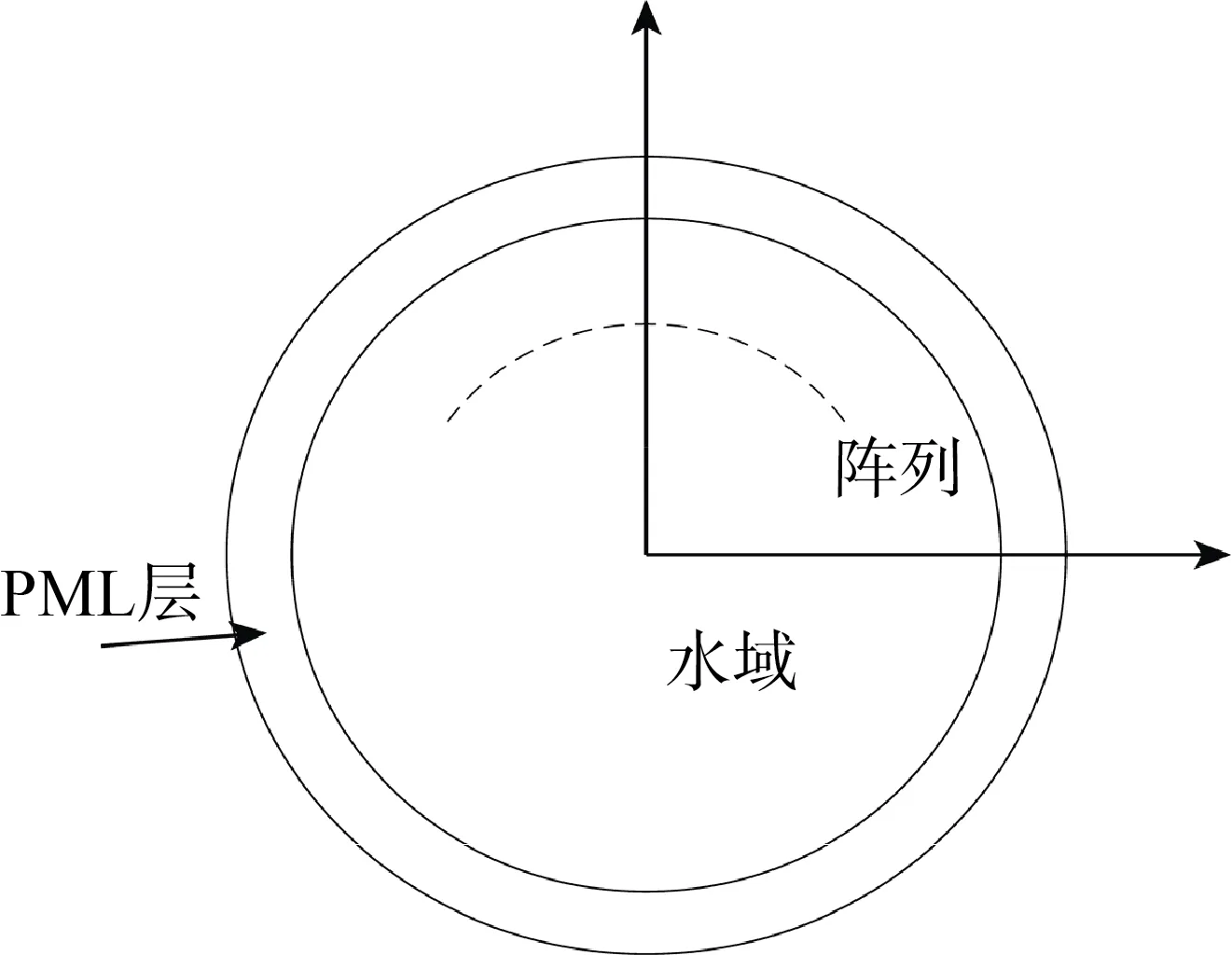
图6 活塞阵列有限元模型示意图Fig.6 Schematic diagram of finite element model for piston array
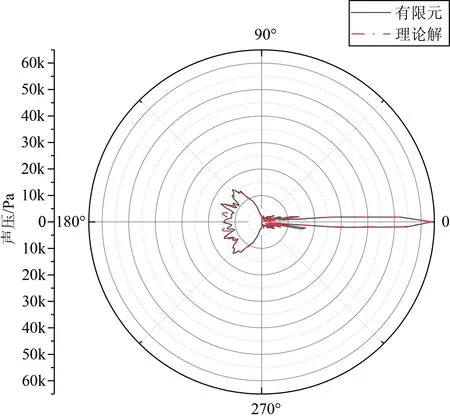
图7 活塞阵列r=1 000 m 指向性图Fig.7 Directivity pattern of piston array at r=1 000 m
3.3 透声窗遮挡损失计算有限元验证
为验证本文提出方法的准确性,下面将建立一个简单的二维模型,分别采用本文方法与有限元法对模型的遮挡损失进行计算,并对结果进行对比验证。
在计算时,取阵列发射角度为0°,通过改变阵列发射方向与透声窗中轴的夹角θx,可以在扫描扇面内进行周向扫描,取遮挡前后阵列平面内沿着阵列发射方向距阵列中心r=1 000 m 处的场点声压级之差,为模型在θx角度时的遮挡损失,记为SL(θx),即
式中:LP(θx)为遮挡前的场点声压级,LP'(θx)为遮挡后的场点声压级。以θx为周向坐标,SL(θx)为径向坐标,绘制极坐标曲线,就可以表征透声窗全向的遮挡损失特性。
以一椭圆模型为验证模型,椭圆长半径为2.3 m,短半径为1.8 m,椭圆中心在原点,截取长边顶点两边各5/16 椭圆弧长作为透声窗,其余弧为吸声侧壁验证模型的阵列参数与3.2 节一致,全局坐标系原点与阵列中心重合。模型示意图如图8所示。
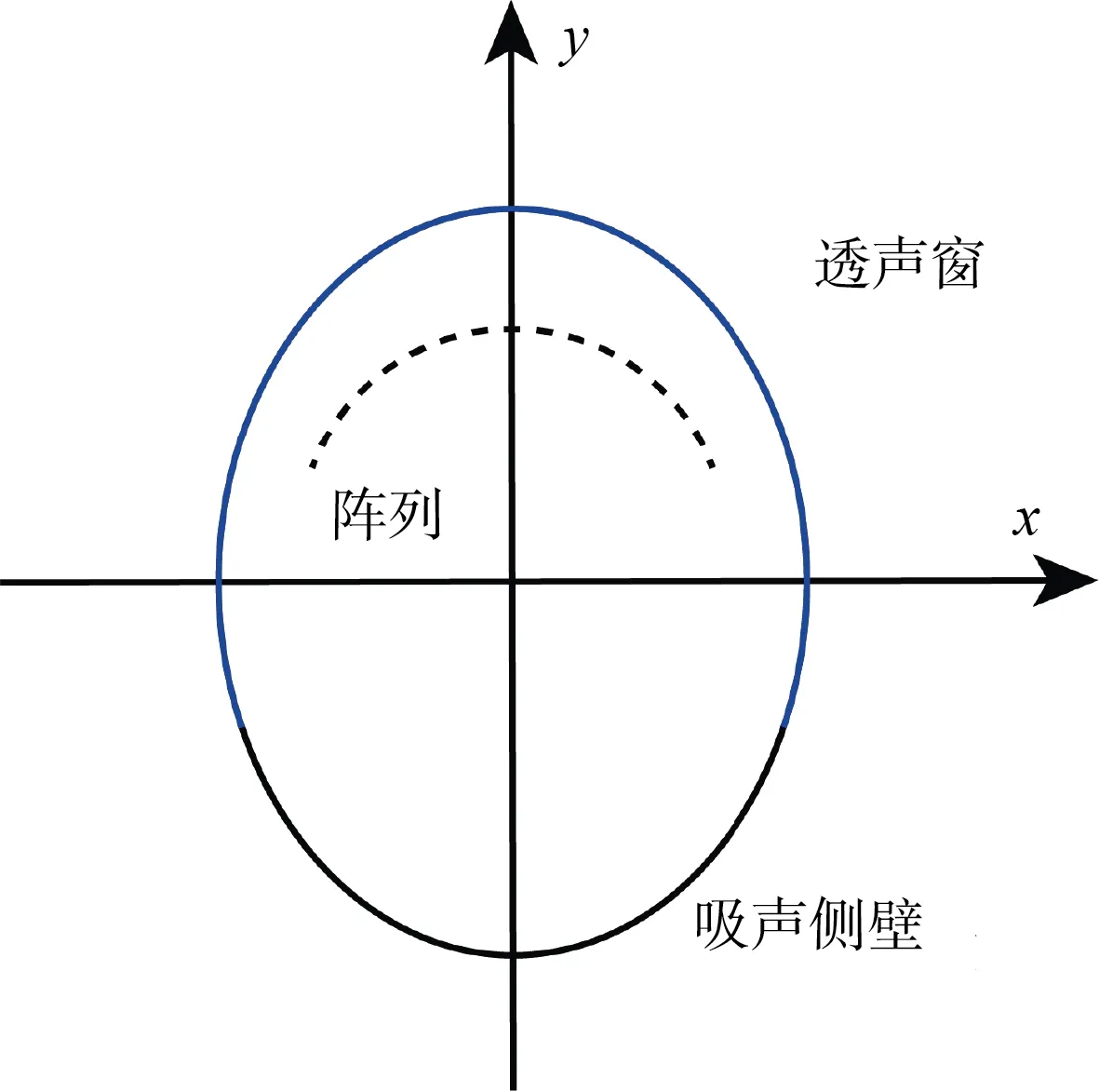
图8 验证模型示意图Fig.8 Schematic diagram of verification model
分别采用纯有限元和解析–数值混合方法得到的模型全向遮挡损失计算结果如图9所示,可以看到,本文提出的方法准确性较高,且相较于有限元,该方法无需建立出完美匹配边界和复杂的阵列活塞声源,模型简单,计算效率较高。
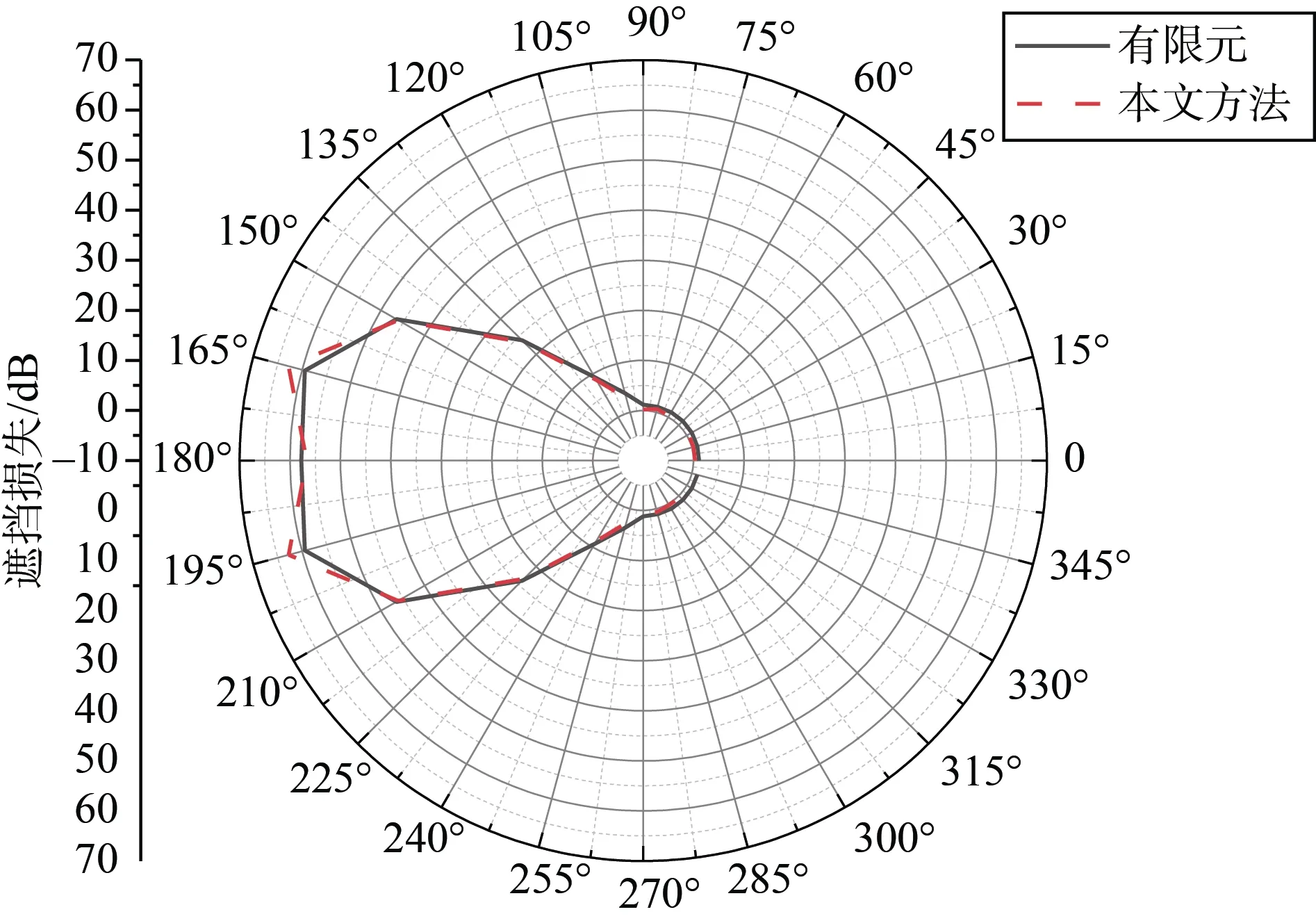
图9 模型全向遮挡损失结果对比Fig.9 Comparison of results of model omnidirectional obstruction loss
4 结束语
本文提出了一种用于透声窗遮挡损失计算的解析–数值混合方法,并通过二维简单模型进行了方法验证,得到了以下结论。
1)球谐波展开法可以有效求解二维活塞声场,结果与有限元吻合较好,本文对各子域的声压函数假设合理。
2)不考虑活塞间的相互作用,运用叠加原理,可以较准确的计算出活塞阵列的声场分布,计算结果与有限元吻合较好,阵列定向发射时,声能量主要集中在发射方向上。
3)本文提出的解析–数值混合方法可以较准确的预报二维透声窗模型的全向遮挡损失,思路清晰,计算简单,相较于纯有限元方法,不涉及无限域的模拟,也不需要建出活塞阵列(纯有限元模型一般在活塞阵列附近网格质量要求较高),对硬件要求较低且耗时较短。
后续可以依据这一思路,继续将该方法拓展至三维模型,方法快速性的优点将得到更充分的体现。
