具有非线性能量阱的双层隔振系统抗冲击分析
2023-06-26李天匀陈树鑫
陈 森,朱 翔,3,*,李天匀,3,陈树鑫
(1.华中科技大学 船舶与海洋工程学院,湖北 武汉 430074;2.华中科技大学 船舶和海洋水动力湖北省重点实验室,湖北 武汉 430074;3.上海交通大学 高新船舶与深海开发装备协同创新中心,上海 200240)
0 引言
近些年来,非线性能量阱(Nonlinear Energy Sink,NES)作为一种被动控制技术的减振装置,以其构造简单、减振频带宽、鲁棒性好等优点逐渐在工程领域中得到广泛关注[1]。非线性能量阱通过靶向能量传递(Target Energy Transfer,TET),能够快速、单向不可逆地俘获主体结构的振动能量,并通过自身的阻尼元件耗散能量。
目前,NES 技术正逐渐被应用到各个工程领域。LUO 等[2-3]通过爆炸试验研究了具有NES 的九层建筑结构的抗冲击性能,结果表明:NES 可以快速减低结构的整体响应。楼京俊等[4-5]针对舰船垂向振动减振需求,设计了一种可垂向承载的柔性铰链型NES 装置,试验结果表明:该装置具有较好的宽频减振效果。此外,该技术还广泛应用于机械工程[6]、能量采集[7]等领域,但目前该技术在船舶领域相关的工作相对较少。
随着导弹、水中兵器的快速发展,爆炸当量与冲击持续时间显著增加,导致舰船面临着严峻的冲击环境。对于舰船隔振装置冲击防护,许多学者开展了大量的研究工作。苏智伟等[8]提出了一种含负刚度动力吸振的混合隔振系统,为高传递损失抗冲器的设计有着借鉴意义。LEDEZMA-RAMIREZ 等[9]通过切换隔振器的刚度,提出了一种半主动开关控制策略,这种半主动控制系统优于线性被动系统。FRANCISCO 等[10]提出了一种具有低动态刚度的隔振系统,与线性系统相比,该系统有利于改善冲击隔离。
本文旨在探索NES 技术对舰船设备抗冲击防护效果。首先建立了具有NES 的双层隔振系统动力学模型,利用三折线冲击谱来模拟基座受到水下爆破时的冲击波,并通过Runge-Kutta 法计算系统的瞬态响应,通过能量分析法讨论了非线性刚度、阻尼、附加质量对设备的抗冲击效果的影响。
1 理论模型
双层隔振系统的隔振效果优于单层隔振系统,被广泛作为舰船机电设备的隔振装置。本文研究的非线性能量阱双层隔振系统模型示意图如图1所示。图1(b)中,基座的质量为M,通过线性刚度k1,阻尼c1与中间质量m1相连;中间质量m1通过线性刚度k2,阻尼c2与设备m2相连。NES 装置通过立方非线性刚度kN及阻尼cN与附加质量m3耦合连接。在基座上施加双峰正弦加速度冲击波a。
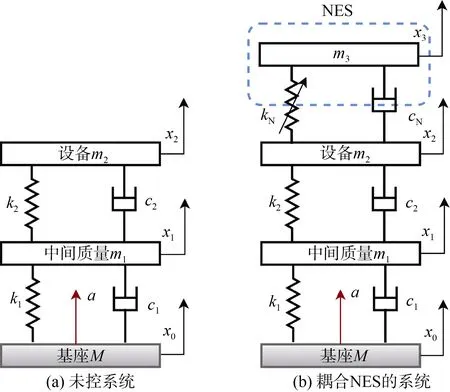
图1 双层隔振系统计算模型Fig.1 Calculation model of two-stage vibration isolation
根据牛顿第二定律,具有非线性能量阱的双层隔振系统动力学方程为:
式中,x0、x1、x2、x3分别为系统的位移。
图1(a)中的未控双层隔振系统动力学方程与图1(b)描述的方程类似。本文采用Runge-Kutta法求解系统的瞬态响应。
当舰船受到水下爆破冲击时,传递到设备的响应在频域上表现为三折线冲击谱(位移–速度–加速度)。通过各种波形的组合才能得到三折线冲击谱,这与一般的机械冲击不同。其中最大谱位移、最大谱速度、最大谱加速度分别为d0、V0、A0。考虑到系统在受冲击时的谱跌效应,需要将实际冲击响应谱转化为双峰正弦波信号,可表述为
其中双峰正弦波的参数为
给定冲击谱d0=0.03 m,V0=2 m/s,A0=1 000 m/s2下的双峰正弦加速度冲击波如图2所示,本文以该冲击波分析非线性能量阱对双层隔振系统的抗冲击影响。
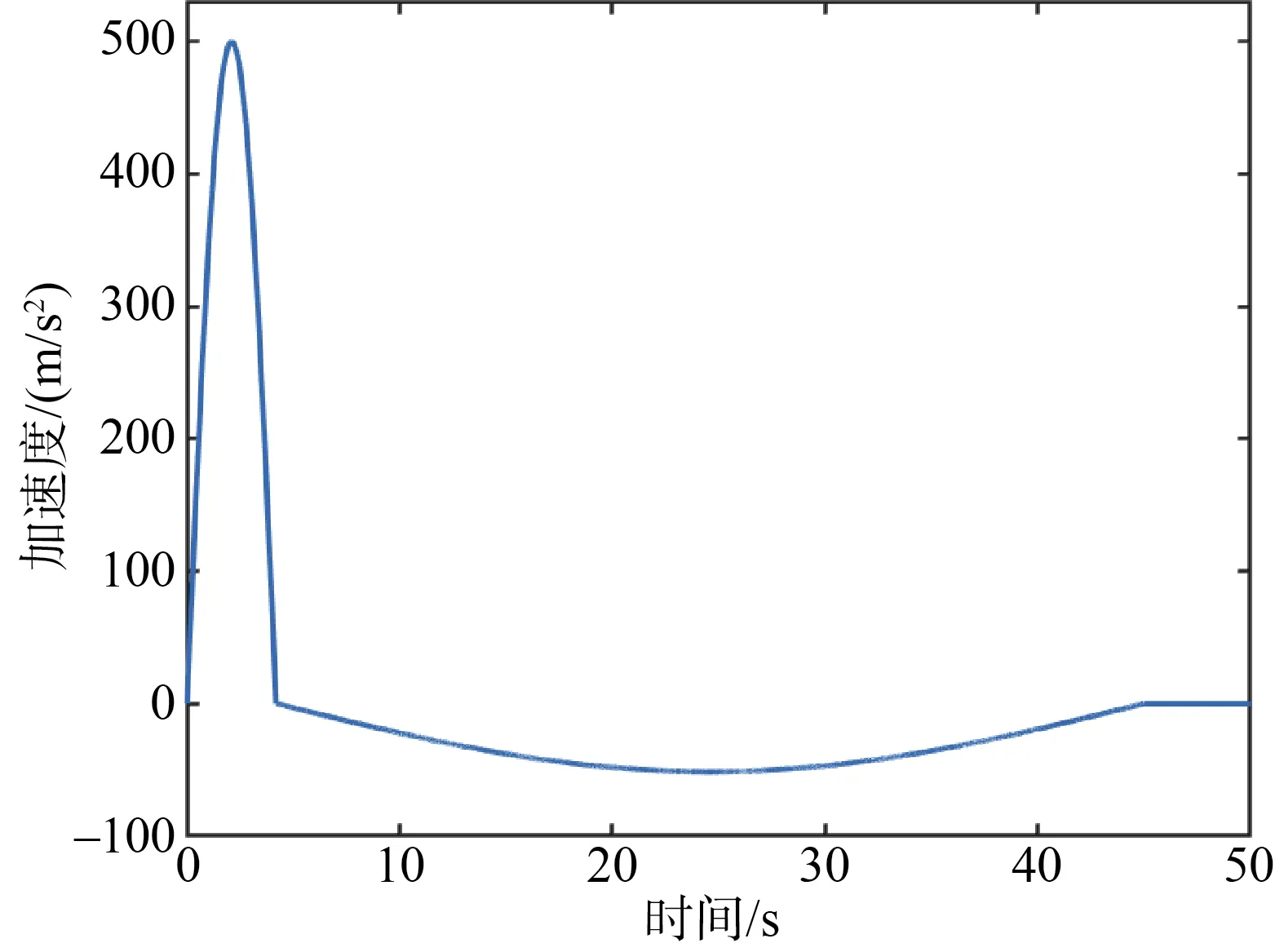
图2 双峰正弦加速度冲击波Fig.2 Double peak sine acceleration shock wave
2 系统抗冲击特性分析
双层隔振系统的参数分别取为:基础M=100 kg,m1=0.4 kg,m2=1 kg,k1=7 000 N/m,k2=5 000 N/m,c1=3 N·s/m,c2=5 N·s/m。非线性能量阱参数为:kN=1×106N/m3、cN=5 N·s/m、μ=10%,其中μ=m3/(m1+m2)。
本文首先对比了机械设备在双峰正弦加速度冲击波下的相对位移与绝对加速度,如图3所示。从图3中可见,在冲击后的100 ms 内,NES 对设备抗冲击性能的改善作用有限;但随着时间的增长,附加在设备上的NES 有效控制了其相对位移与绝对加速度。

图3 机械设备的冲击响应对比Fig.3 Comparison of shock response of equipment
本文进一步采用能量分析法来讨论分析NES 非线性刚度kN、阻尼cN和质量比μ对设备的抗冲击性能的影响。设备的瞬时机械能可以写为
在时间t内存储在设备的总能量可以写为
下面定义了2 个评价参数来评估NES 的抗冲击效果,即
式中:Eu为未控系统设备的瞬时机械能;En为耦合NES 系统设备的瞬时机械能;Wu为未控系统设备在时间t内的总能量;Wn为耦合NES 系统设备在时间t内的总能量。
通过NES 阻尼耗散的总能量可以写为
上文定义了3 个评价参数η1、η2、Wd来评估NES 的抗冲击效果,其中η1、η2越小,Wd越大,说明NES 抗冲击效果越好。
保持NES 的参数不变,机械设备的瞬时机械能如图4所示。从图4可见,未控系统的瞬时机械能先是快速增大,冲击结束后,则是在震荡中缓慢下降;耦合NES 设备的瞬时机械能则可以快速下降,在500 ms 左右几乎为0。

图4 机械设备的瞬时机械能对比Fig.4 Instantaneous mechanical energy of equipment
保持NES 非线性刚度kN、阻尼cN不变,研究质量比μ对评价参数η1、Wd的影响,如图5所示。从图5(a)中可见,在冲击后的100 ms 内,增大质量比μ对设备抗冲击性能的改善作用有限;当质量比μ较小时,在冲击后的较长时间内,η1依然很大;当质量比μ较大时,η2可以快速下降10%以下。从图5(b)中可见,选取适当的质量比μ可以使得NES 阻尼耗散的能量Wd快速增大。
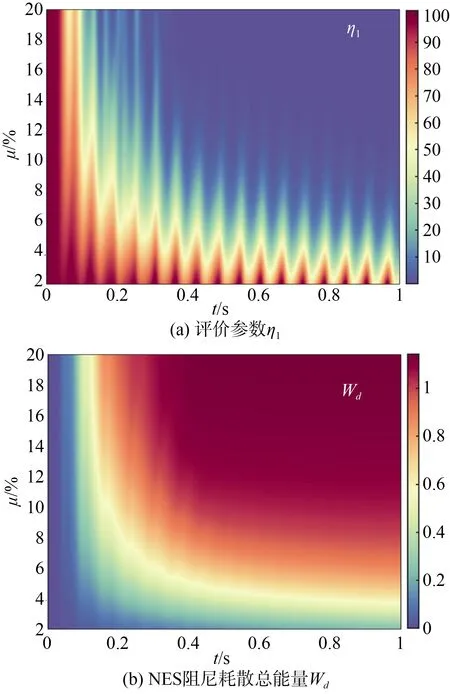
图5 质量比μ 对抗冲击效果的影响Fig.5 Effect of mass ratio μ on the impact resistance effect
保持NES 质量比μ、阻尼cN不变,研究非线性刚度kN对评价参数η1、Wd的影响,如图6所示。从图6中可见,非线性刚度kN存在着一个最优值,使得η1最小、Wd最大;当非线性刚度kN较大时,会恶化NES 的抗冲击效果(η1>100%)。保持NES质量比μ、非线性刚度kN不变,研究阻尼cN对评价参数η1、Wd的影响,如图7所示。从图7中可见,阻尼cN也存在着一个最优值,使得η1最小、Wd最大;当阻尼cN较小时,在冲击后的400 ms 内,此时的η1较大,不利于改善设备的抗冲击性能。

图6 非线性刚度kN 对抗冲击效果的影响Fig.6 Effect of nonlinear stiffness kN on the impact resistance effect

图7 阻尼cN 对抗冲击效果的影响Fig.7 Effect of damping cN on the impact resistance effect
下面进一步研究NES 质量比μ、非线性刚度kN、阻尼cN同时对抗冲击效果的影响。为此,本文分别计算了冲击后100 ms、500 ms 内的η2与Wd,来评估其对抗冲击效果的影响,二维等高线图分别如图8、图9所示。
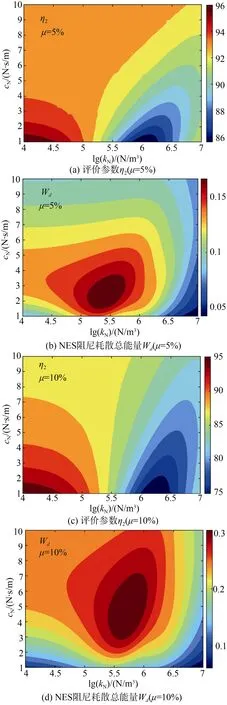
图8 冲击后100 ms 内NES 参数对抗冲击效果的影响Fig.8 Effect of NES parameters on the impact resistance effect within 100 ms after the impact

图9 冲击后500 ms 内NES 参数对抗冲击效果的影响Fig.9 Effect of NES parameters on the impact resistance effect within 500 ms after the impact
从图8中可见,NES 非线性刚度kN、阻尼cN对η2、Wd的影响规律不同,其对应的最优参数范围不同。从图8(a)、(b)中可见,当质量比μ较小时(5%),在最优参数范围内,η2约为86%,Wd仅约为0.15 J,抗冲击效果不佳;从图8(c)、(d)中可见,增大质量比μ(10%),在最优参数范围内,η2约为75%,Wd约为0.3 J,抗冲击效果得到了一定的改善。从图9中可见,随着时间的增长,NES 非线性刚度kN、阻尼cN对η2、Wd的影响规律相似。从图9(a)、(b)中可见,当质量比μ较小时(5%),在最优参数范围内,η2约为40%,抗冲击效果良好;从图9(c)、(d)中可见,增大质量比μ(10%),在最优参数范围内,η2下降到了30%以下,Wd约为1 J,且最优参数范围更大,其鲁棒性较好。
3 结束语
本文分析了具有非线性能量阱的双层隔振系统抗冲击效果。通过能量分析法讨论了非线性能量阱参数对其抗冲击性能的影响。针对本文给出的计算模型,得到了以下结论:
1)NES 非线性刚度kN、阻尼cN存在着最优参数,适当的质量比μ就可以显著提升NES 的性能。
2)在设备受到冲击波作用后的0~100 ms 内,即使在最优参数范围内,NES 对设备抗冲击性能的改善作用有限;在冲击后500 ms 内,NES 显著降低了设备的冲击能量,抗冲击效果好。
3)本文研究的内容,可对舰船隔振装置冲击防护提供参考。
