妙用数形结合 让初中生数学解题思路更清晰

摘 要：要想巧妙运用有效的数学解题技巧，需要能够深刻理解数学概念并能灵活运用数学知识.本课题的研究是基于数形结合视角，引导学生展开数学问题的解答，以使学生能够在解题之中寻求技巧的运用之法，更好地将数学解题技巧灵活、巧妙运用.通过课题内容的分析，帮助学生构建清晰的数学解题思路.

关键词：初中数学；数形结合；思维；方法

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2023）02-0008-03

在众多解题方法中，数形结合是数学常用的一种解题技巧，能够给数学教学带来很大的推进作用.初中数学知识中存在大量数与形的关系，利用数形结合思想，引导初中生展开对数学问题的解答，构建起问题中数与形的关系，是一个值得研究与探索的课题.本文主要是寻找数形结合思想的应用之法，从对数形结合思想的理解与分析，到解题技巧的应用注意点，再到数形结合的应用方法探索，一路展开课题分析，以做到对数形结合思想的有效探索，从而引导初中生形成良好的数形结合解题意识.

1 数形结合的概念及应用意义

1.1 数形结合概念

数学问题之中大多存在着“数”与“形”的关系，将二者联系起来，突破单方面的思维探究，即是一次数与形的结合.在解题过程中以数促形、以形观数，让整个数学问题能够迎刃而解，这就是数形结合思想.

1.2 数形结合思想应用意义

首先，将数形结合思想应用于数学问题的解答，可以构建起数与形之间的联系，让数学问题不再单单是解答一方面的关系，而是二者的思维融合与探讨，使整个数学问题解答变得有趣味，有层次；其次，数形结合思想也能够让原本复杂的数量关系变得简单，学生不用再去计算大量的数量关系，可以直接观察由题目给出的图形关系，结合具体的数量关系内容，展开问题的规律解答，大大降低了解题的错误率，同时解答的时间也能够大大缩短，有利于数学问题解答质量的整体提升.

2 数形结合解题技巧的应用注意点

2.1 懂得从全局出发

学生要能从全局出发，学会观察由数量之间的关系能构建出一个图形关系，反之出现一个图形关系，可以将其转化为数量关系.教师要引导学生做好数量与图形之间关系的思考与探索，搭建起一条彼此相互联系的桥梁.

2.2 懂得从简思维

运用数形结合思想解题是为了让数学解题变得有逻辑、有技巧、有效率，是将一个数学问题由难到简的过程，因此学生要有一个从简思维，学会从问题中寻找简便的解答方式.

2.3 懂得概念掌握

在解答一些复杂的方程问题时，如果学生没有掌握好方程的概念，或不懂得从方程之中寻找到与之对应的函数关系，就无法将一个数量关系转为图形关系.因此，做好学生对数学概念知识的认识与理解尤为重要，是教师教学的重中之重.

3数形结合解题技巧应用于初中数学问题解答的方法

3.1 数形结合与初中数学函数解题

在数学学习中，多数学生都喜欢用数量关系来解答问题，导致计算时间过长，既耽误解题的时间，也容易产生解题失误.函数问题一直是初中数学的一个重要问题，鼓励学生应用数形结合思想解答函数问题，是一种有效的初中数学解题教学.

学会应用数形结合思想解答初中函数问题，要先从初中数学问题之中获取到函数中的数量关系.再由这些数量关系信息构建起函数的图像，由函数图像去破解问题之中的数量关系，从而将看似复杂的函数问题从简解答.根据数与形构建起来的关系，从一个整体层面去解答函数问题，可以使学生不只去思考一个数字或者一个图形的问题.

下面让我们看一个初中数学函数问题：在平面直角坐标系中，分别过点A（m，0），B（m+2，0）作x轴的垂线l1和l2，探究直线l1，直线l2与双曲线y=3/x的关系.请解答如下的问题：

（1）当m=1时，两直线与双曲线的交点到原点的距离是否相等？

（2）两直线中总有一条与双曲线相交吗？

（3）当﹣2＜m＜0时，两直线与双曲线的交点在y轴两侧吗？

（4）当两直线与双曲线都有交点时，两交点的最短距离是否为2？

解题分析 根据题干中的信息条件，可以构建起数量与图形间的关系.即看到了题目中的坐标信息及双曲线，可以快速地从大脑之中检索出反比例函数的图象绘制方法，思考如何利用这些信息去构建图形，同时，问题中提到的x轴的垂線l1和l2也是用于图象绘制的条件，所以应先去构建一条数与形结合的解题思路，再去展开具体问题的解答.

解题过程 可知题中双曲线可以看作是一个反比例函数，画出函数图象，如图1所示：

首先，思考到y轴是反比例函数图象的渐近线，且题中两条垂线之间的距离为2，就会得到一个结论：这两条垂线必有一条与反比例函数图像相交，从而可以得到第二个问题的答案.其次，根据条件，我们可以得到m=1时，ｌ1为x=1，ｌ2为x=3.此时两直线与双曲线的交点分别为M（1，3），N（3，1），利用勾股定理可得MO=NO，从而得第一个问题的答案.最后，根据题目给出的条件信息，可以得到当l2和y轴重合时，即m+2=0，此时m=-2，当l1和y轴重合时，即m=0，进而可知第三个问题是正确的.由此证明下去，分别画出双曲线和直线l1、l2有两个交点的三种情况，可得MN>2，故第四个问题的结论是错误的.

解题反思 从本问题的解答过程可以看出，数形结合思想的应用会让问题解决变得简单且有效，有利于学生探究出其中的数学

规律，有助于提升学生的数学解题效率和质量.

3.2 数形结合与初中数学全等三角形判定学生要懂得去思考如何在一个复杂几何图形之中，将数量关系寻找出来，要能从问题之中构建图形，再由图形来分析出数量关系，从图形中寻找到解答问题的突破口.

请看下面这道全等三角形判定问题：如图2，已知D是AB的中点，∠ACB=90°，求证CD=12AB.

解题分析 根据题目中提供的各种信息，可以知道这是一个关于全等三角形判定的几何问题.但若只是直观地去看图形，不会应用其中的数量关系去解答，解题也很困难.因此，教师要引导学生利用全等三角形的判定方法，去构建起以形助数的思路，将图形之中的数量关系写出来，以帮助获得解题思路.

解题过程 先延长CD至P点，使D为CP中点，连接AP，BP.因为DP=DC，DA=DB，所以四边形ACBP为平行四边形，又因为∠ACB=90°，所以平行四边形ACBP为矩形；∴CD=DP=1／2AB.

解题反思 从解题的过程可以看到图形是存在的，但是学生必须学会利用图形之中的条件信息，去构建起一个数学计算过程，才能有利于推进解题的开展与落实，有利于提升证明的效率和质量.解题过程中，很多学生能看到边的数量信息，却没有真正看到数量与图形之间的关系，不会利用数量与图形的关系进行问题的解答，从而导致解答出来的内容无效或者错误，无法快速获得问题的答案.所以，在反思这道问题的解决过程时，学生要懂得从图形之间的逻辑结构之中探究其中的数量关系，这样才能有效寻求出问题的答案.

3.3 数形结合与初中数学不等式解答

初中数学中的一些不等式问题，也可以利用数形结合思想，将不等式与图形构建起联系，将不等式问题转化为图形关系去解答，这样的解题过程会很有趣，有利于学生寻找到更快、更高效的解题路径.教师可以结合具体的不等式例题，引导学生学会去对照数形，探寻二者间相互渗透的方式，以提升解题的效率.学生要能从不等式概念知识之中寻找数与形的关系，學会利用概念去构建自己的大脑思维.在这个过程中，教师是引导者，要带领学生去探索数与形的关系，体会思考问题的方式.

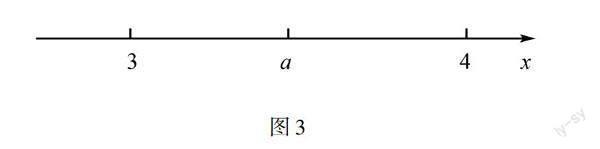
如下题所示内容：根据图3，使不等式|x-4|+|x-3|

解题分析 先分析题中给出的不等式，可以知道|x-4|+|x-3|表示数轴上x所对应的点到与4、3所对应的两点的距离之和，结合图3可分析出其和的最小值为1，从而即可获得a的取值范围.

解题过程 先根据“|x-4|+|x-3|”提示的信息，在数轴上标注对应的点，由x对应的点到与4、3所对应的两点距离之和大于等于1，可知a>1.

解题反思 学会利用数轴上的信息，构建起不等式与图形之间的关系，将难度很大的问题转化为简单问题，是数形结合思想在解题中的有效体现.

综上所述，通过巧妙应用数形结合思想，学会将这个思想应用于多种数学问题解答之中，是能够提升解题效率的途径，有助于学生掌握到有效的解题技巧.

参考文献：

［1］李建成.论数形结合在初中数学教学中的有效运用[J].魅力中国，2022，8（14）：58-58.

[2] 李敏瑞.数形结合在初中数学解题过程中的妙用[J].课程教育研究，2021，3（5）：99-102.

[3] 陈元军.分析数形结合在初中数学解题中的应用思路[J].速读旬刊，2020，21（7）：54.

[4] 吴吉星.数形结合对培养初中生数学思维的价值探讨[J].新课程导学，2021，3（11）：9-16.

［责任编辑：李 璟］

收稿日期：2022-10-15

作者简介：黄汉财（1976.11-），男，福建省平和人，本科，中学一级教师，从事初中数学教学研究.