混合介质层类同轴硅通孔等效电路模型的建立与验证

王晗，蔡子孺，吴兆虎，王泽达，丁英涛

（1.北京理工大学 集成电路与电子学院，北京 100081；2.紫光展锐(上海)科技有限公司，上海 200120；3.北京理工大学 徐特立学院，北京 100081）

近年来，以穿透硅通孔（through-silicon-via，TSV）为关键结构的三维集成技术在无线与射频领域有着广泛的应用[1−3].然而，由于三维集成技术中常使用的硅衬底具有阻值较低、介电常数大、损耗较高等缺点，传统的TSV 信号结构在高频领域的应用中会遇到传输损耗大、抗电磁干扰能力差、易产生耦合噪声等问题,从而严重制约了相应的射频微系统的性能.因此，新材料的开发和使用、新型射频TSV 的研究及市场化应用就显得尤为重要.

近年来，为了解决传统TSV 在高频领域中面临的问题.2008 年，HO 等[4]提出一种同轴TSV（coaxial TSV，CTSV）结构来改善其高频信号传输性能[4].该结构由中心信号TSV，接地的金属屏蔽层以及填充在二者之间的环形介质层组成，其具有自屏蔽和抗电磁干扰的能力并可以有效降低信号传输损耗和耦合噪声.同年，CURRAN 等[5]采用具有低介电常数的苯并环丁烯（Benzocyclobutene, BCB）作为中心信号TSV和金属屏蔽层之间的介质层，如图1（a）所示.该结构显著提升了CTSV 的电学性能并降低了整体结构尺寸，进一步满足了射频领域的信号传输需求.2020 年，WU 等[6]针对BCB 介质层CTSV 进行了热机械可靠性分析，发现BCB 介质层能起到一定的应力缓冲作用，从而降低CTSV 的热应力水平.2017 年，WANG等[7]在BCB 介质层CTSV 的基础上，利用了低阻硅的良好导电性,采用低阻硅代替Cu 作为中心信号导体与外层屏蔽环（低阻硅−BCB−低阻硅），设计并制备了低阻硅CTSV，在保证信号传输性能的前提下，降低了工艺复杂程度.2021 年，DENG 等[8]进一步对低阻硅CTSV 的热力学性能进行了分析，确认了其良好的热力学可靠性.不过，由于是制备在低阻硅衬底上，这将在一定程度上限制低阻硅CTSV 的应用领域.此外，在不改变中心导体材料的前提下，为了降低成本和工艺难度，2011 年，NDIP 等[9]使用了混合介质层（高阻硅−BCB−高阻硅）来替代BCB 介质层，得到了混合介质层CTSV（CTSV with mixed dielectric layer，MD CTSV）结构，如图1（b）所示.虽然上述CTSV在高频信号的传输方面有极大的优势，但其中心信号TSV 和金属屏蔽环的同步制备难度非常大，这限制了其进一步的应用.2013 年，CHIEN 等[10]采用一组环绕中心信号TSV 的接地TSV 来代替原本的金属屏蔽环，在保证了良好的高频信号传输性能的情况下，降低了工艺难度.该结构被称作类同轴TSV（Coaxially-shielded TSV，CSTSV）结构，如图1（c）所示.在2021 年，本课题组结合MD CTSV 和 CSTSV 两种结构的优点，提出了一种混合介质层CSTSV（CSTSV with mixed dielectric Layer，MD CSTSV）结构并给出了相应的制备工艺流程[11].该结构如图1（d）所示，混合介质层结构同样为高阻硅−BCB−高阻硅，其截面如图1（e）所示.该结构在实现良好的高频信号传输性能的前提下，进一步降低了结构的体积占比，优化了工艺流程，并减少了工艺成本，在高密度射频封装领域中具有极大的应用前景.

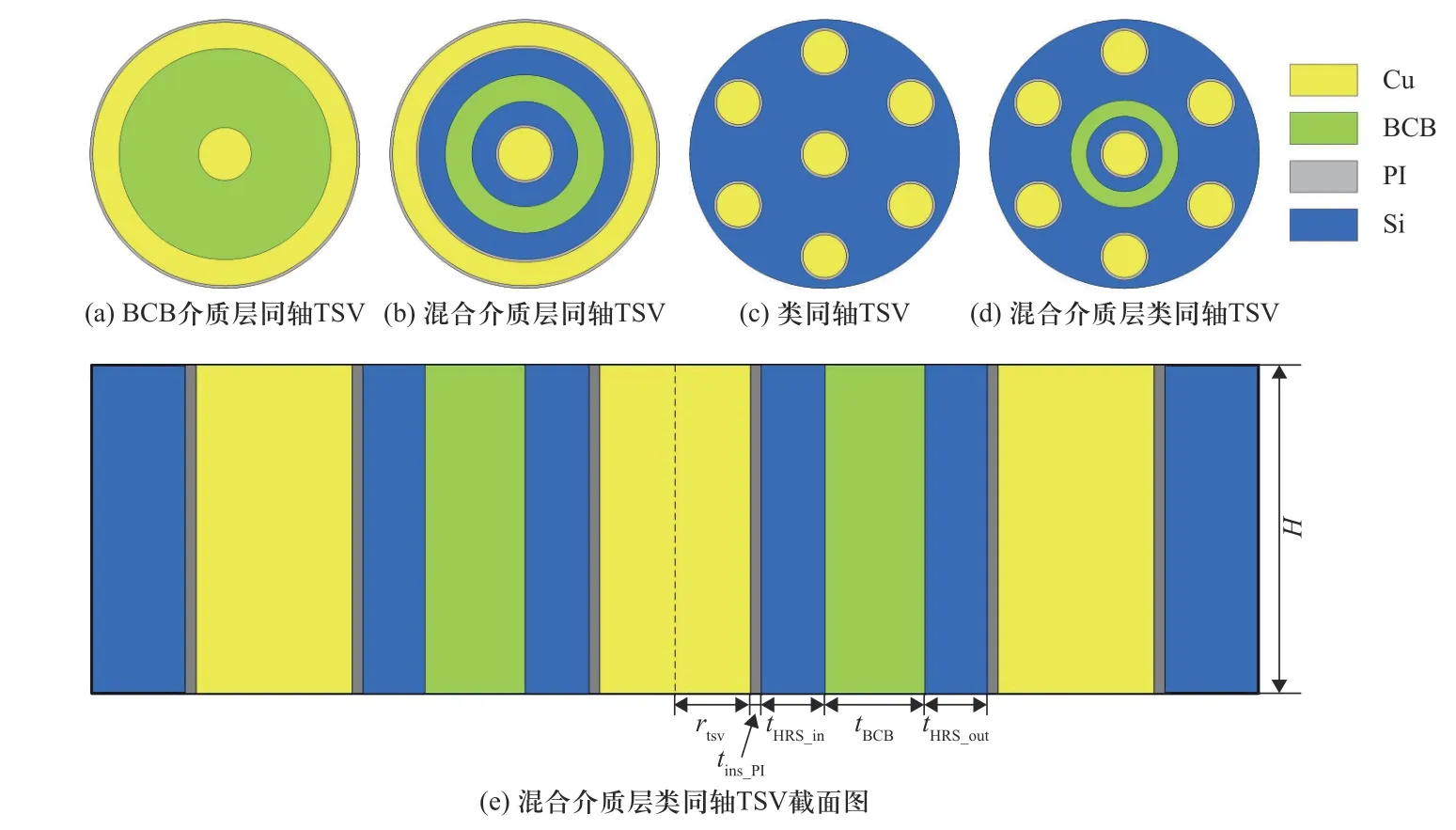
图1 4 种同轴 TSV 结构示意图以及混合介质层类同轴 TSV 截面示意图Fig.1 Schematic diagram of four kinds of coaxial TSV structures and schematic cross-sectional view of coaxial shielded TSV with mixed dielectric layer

对于上述应用于高频领域的TSV 结构，构建可精准、直观、便捷地反应TSV 信号传输性能的等效电路模型也引起了工业和学术界的广泛关注.考虑到在高频信号传输环境下寄生效应对TSV 电学性能的影响较为显著，实现对TSV 单位长度RLGC 电学参数的精确提取与分析将是构建其等效电路模型的关键，并对其电学特性与可靠性的研究具有重要意义.2012 年，XU 等[12]研究了CTSV 结构在40 GHz 频率下材料属性和几何参数对其电学性能的影响，并建立了一种宽带SPICE 模型以匹配CTSV 的全波仿真结果，促进了三维系统设计和评估.2013 年，LIANG等[13]基于静磁场理论提出了计算CTSV 的单位长度电阻和电感的闭式公式，并提出了一种宽带等效电路模型.2017 年，QU 等[14]采用多导体传输线理论对被多根接地TSV 包围的信号TSV 结构的单位长度RLGC 电学参数进行了推导计算.2017 年，WANG 等[7]针对基于低阻硅的CTSV，利用T 模型电路，建立了相应的RLGC 等效电路模型.2018 年，MEI 等[15]提出硅芯CTSV 结构的电学参数计算公式，并针对硅芯CTSV 在不同材料以及几何尺寸下的电学性能进行了研究.不过，当前针对MD CSTSV 的单位长度RLGC 电学参数的提取与等效电路模型的建立尚未见到报道.基于此，本文针对MD CSTSV，通过多导体传输线理论和引入比例因子λ的环形介质层的复电容的计算公式提取了该结构的单位长度RLGC 电学参数, 建立了相应的等效电路模型，并对该单位长度RLGC 电学参数提取方法与等效电路模型的准确性进行了仿真验证.

1 MD CSTSV 单 位 长 度RLGC 电 学参数的提取

1.1 单位长度等效R、L 电学参数的求解

考虑到MD CSTSV 的混合介质层结构较为复杂，首先针对具有单一介质层结构（高阻硅）的CSTSV的单位长度等效R、L电学参数进行推导计算.与常规的CTSV 不同，由于CSTSV 具有多根TSV 结构，可采用多导体传输线理论对其单位长度R、L电学参数进行提取[14].图2 给出了1SnG CSTSV（包含1 根中心信号TSV 和外围n根接地TSV，各根TSV 的几何尺寸均相同）结构的电学参数模型.其中，将某一接地TSV 编号为#0，信号TSV 编号为#1，其余接地TSV依次编号为#2，#3 ，···，#n.

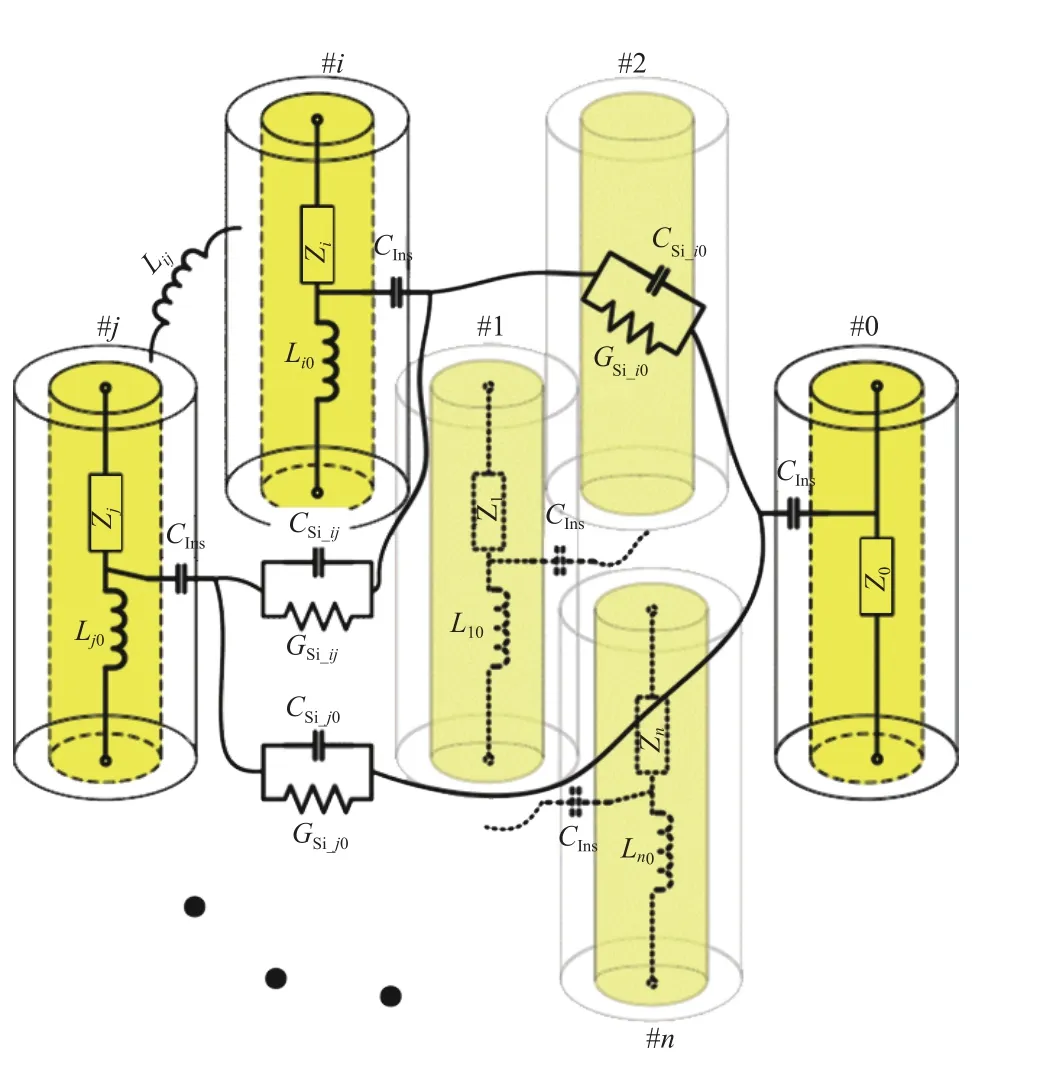
图2 1SnG CSTSV 等效电学参数与模型Fig.2 Equivalent electrical parameters and models of 1SnG CSTSV

对于CSTSV 结构中的单根TSV 结构，其自身的单位长度自感(Lii)和不同TSV 结构之间的单位长度互感(Lij)可分别通过式（1）和式（2）计算得到.其中，μCu为TSV 的中心导体材料Cu 的磁导率，rTSV为TSV的中心导体半径，Pi0为编号#i的TSV 与#0 号接地TSV之间的中心距离，Pij为编号#i和#j的TSV 之间的中心距离.

基于多导体传输线理论，可以得到如式（3）所示的矩阵形式来表示CSTSV 的单位长度电感.

式中，Vi代表#i号TSV 与接地的#0 号TSV 之间的电压差.考虑到接地TSV 彼此相连，它们相互之间则可视为短路，即V2,V3,···,Vn均等于0.因此，式（3）可简化为

其中：

同时，基于回路电感的定义可知：

式中：Leq代表CSTSV 的单位长度等效电感；ω表示为角频率.结合式（4）～（7），可以得到Leq的解析表达式为

此外，对于CSTSV 结构中#i号TSV 的内部阻抗Zi，其可用式（10）计算求得.式中σCu为TSV 的中心导体材料Cu 的电导率，函数B0和B1分别为零阶和一阶的第一类修正贝塞尔函数.

基于多导体传输线理论，同样可以得到如式（11）所示的矩阵形式来表示CSTSV 的单位长度内部阻抗.

考虑到该CSTSV 结构中接地TSV 与信号TSV的几何尺寸相同，所以有Z0=Z1=···=Zn，CSTSV 的单位长度等效内部阻抗Zeq的解析表达式为

基于上述讨论，将求解得到的Leq、Zeq带入阻抗公式中即可得到 CSTSV 的单位长度等效R、L电学参数：

从上述分析中可以看出，CSTSV 结构的单位长度等效R、L电学参数的解析表达式仅与TSV 中心导体半径、信号TSV 与接地TSV 之间的中心距离以及导体材料的属性相关，而和信号TSV 与接地TSV之间的介质层的材料属性无关.考虑到MD CSTSV结构与CSTSV 结构之间仅是介质层结构不同，因此针对CSTSV 结构的单位长度等效R、L电学参数的分析和推导过程同样适用于MD CSTSV 结构，即其相应的单位长度等效R、L电学参数可采用上述公式直接求得.

1.2 单位长度近似G、C 电学参数的求解

对于MD CSTSV 结构的单位长度G、C电学参数，考虑到其混合介质层结构的复杂性和硅衬底的开放性，很难直接求得与各介质层相对应的单位长度G、C电学参数的解析解.因此，尝试基于MD CTSV（混合介质层结构为高阻硅−BCB−高阻硅）的环形介质层的复电容计算公式，通过引入比例因子λ对计算公式进行修正，并利用计算得到的单位长度近似复电容求得MD CSTSV 单位长度G、C电学参数的近似解.

对于MD CTSV 结构的单位长度等效G、C电学参数的提取，可定义其混合介质层的复电容为

式中：ai与bi分别为某一介质层的内半径与外半径；ε0为真空介电常数；εr_i和tanαi分别为某一介质材料的相对介电常数与损耗角正切.对于MD CTSV 结构，BCB 的损耗角正切tanαBCB为0.000 8.高阻硅的损耗角正切tanαHRS可通过下式求得

式中：εr_HRS为高阻硅的相对介电常数；ρHRS为高阻硅的电阻率.

将计算得到各介质层的单位长度复电容串联后，即可得到MD CTSV 的单位长度复电容，将其带入式（16）和式（17），可得到相应的单位长度等效G，C电学参数.

在上述分析的基础上，针对MD CSTSV 结构，若将其混合介质层结构近似为与MD CTSV 一样的环形混合介质层结构，并引入比例因子λ对环形介质层的复电容计算公式进行修正，MD CSTSV 结构的各介质层的单位长度近似复电容则可由下式计算得到

由于MD CSTSV 结构的外导体屏蔽环由环形排布的接地TSV 所构成，在计算外层高阻硅介质层的复电容时，将其外半径的值视作其内半径、外层高阻硅介质层厚度与接地TSV 半径的和，如式（23）所示.

此外，在MD CSTSV 结构中，为确保TSV 结构和高阻硅衬底之间的电学隔离，每根TSV 结构的外围均有一层PI 介质层，这也会引入相应的介质层电容CPI，其可以由环形电容公式直接计算得到

式中：tins_PI为PI 介质层的厚度；εPI为PI 的相对介电常数.TSV 与硅衬底之间的电容阻抗则为

利用式（11）和式（12），同样可得到各TSV 与高阻硅衬底之间的PI 介质层电容所对应的阻抗矩阵和相应的单位长度电容阻抗ZPI_eq.之后，结合MD CSTSV 结构的对称性和各TSV 几何尺寸的一致性，其PI 介质层的单位长度等效电容Cins_PI，单位长度等效电导Gins_PI以及相应的单位长度等效复电容Cˆins_PI由下式表示（PI 的损耗角正切tanαPI为0.004）

将上述分析得到的MD CSTSV 结构中各介质层的单位长度近似复电容与PI 介质层的单位长度等效复电容进行串联，就可以得到MD CSTSV 单位长度G、C电学参数的近似解：

对于比例因子λ的计算，针对1S4G MD CSTSV结构（信号TSV 数量为1，接地TSV 数量为4，其结构尺寸如表1 所示，各结构尺寸的具体含义也在图1（e）中标出），利用Ansys Q3D 仿真软件提取其单位长度等效电容C和 等效电导G并结合计算得到的PI 介质层单位长度等效复电容求得其混合介质层结构的单位长度等效电容CMDins_equ.通过对比，发现基于Ansys Q3D 仿真软件提取得到的混合介质层结构的单位长度等效电容CMDins_equ和将比例因子λ设置为1 时计算得到的混合介质层结构的单位长度电容的近似解基本相等，因此将在1S4G MD CSTSV 结构下提取得到的混合介质层结构的单位长度等效电容CMDins_equ视作基准值，并基于由Q3D 提取的具有不同接地TSV 数量的MD CSTSV 混合介质层结构的的单位长度等效电容值（图3）求得相应的比例因子λ，如式（30）所示.

表1 1S4G MD CSTSV 结构尺寸Tab.1 Structural dimensions of 1S4G MD CSTSV

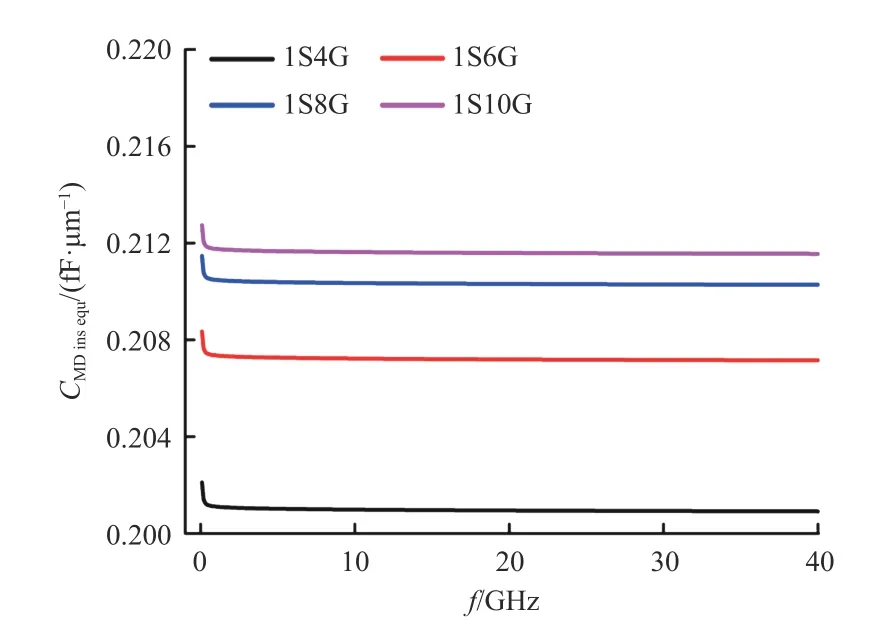
图3 不同接地 TSV 数量下，基于 Q3D 提取的MD CSTSV 混合介质层结构的单位长度等效电容值Fig.3 Equivalent capacitance per unit length of the mixed dielectric layer of CSTSV extracted based on Q3D with different grounded TSV numbers

表2 给出了计算得到的具有不同接地TSV 数量的MD CSTSV 结构所对应的比例因子λ的值.

表2 比例因子 λTab.2 Scale factor λ

最终基于表1 中给出的1S4G MD CSTSV 结构的尺寸，采用上文讨论给出的单位长度等效R、L电学参数和单位长度近似G、C电学参数的求解方法提取了该结构的单位长度RLGC 电学参数，相应的结果如图4 所示.在高频下，单位长度电容C和电感L分别为0.185 fF/μm 和0.34 pH/μm.

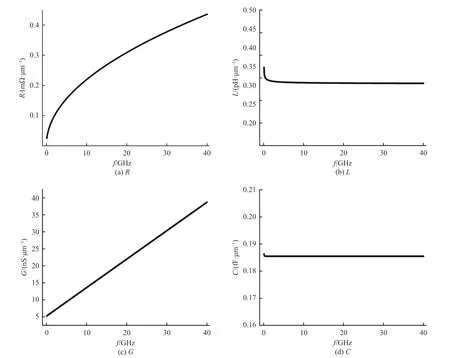
图4 1S4G MD CSTSV 的 RLGC 电学参数的提取结果Fig.4 Extraction results of RLGC electrical parameters of 1S4G MD CSTSV

2 MD CSTSV 等效电路模型的建立与验证

2.1 MD CSTSV 等效电路模型的建立

为了更好地实现TSV 结构与芯片电路系统的协同仿真，人们通常基于T 模型、π 模型或双T 模型电路建立TSV 的等效电路模型.如图5 所示，T 模型电路由一个分支子电路和两个串联子电路构成，π 模型电路则是由两个分支子电路和一个串联电路构成.在T 模型的基础上，若对分支电路进行分流，即可形成包括3 个串联子电路和两个分支电路的双T 模型电路[16].在本工作中，基于T 模型电路，使用ADS 软件建立了1S4G MD CSTSV 结构的等效电路模型，如图6 所示.在该等效电路模型中，1S4GMD CSTSV 结构的各个电学参数均基于前文的分析求得，其中部分不随频率变化的电容C与电导G均在表3 中给出，而电阻R、电感L以及各聚合物介质材料的电导G均随频率发生变化，它们将在ADS 软件中以频变参数的形式由Data AccessComponent 和Z1P_Eqn 组件带入计算.

表3 1S4G MD CLTSV 结构电学参数Tab.3 Electrical parameters of 1S4G MD CLTSV

图5 TSV 等效电路模型Fig.5 Equivalent circuit model of TSV

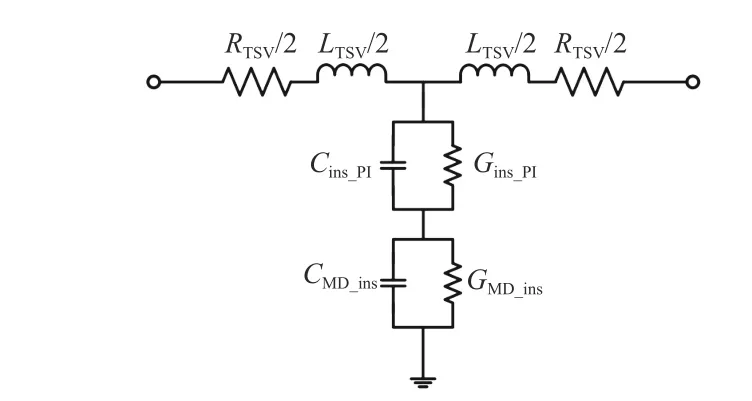
图6 1S4G MD CSTSV 等效电路模型Fig.6 Equivalent circuit model of 1S4G MD CSTSV

2.2 MD CSTSV 等效电路模型的验证

针对所建立的1S4G MD CSTSV 结构的等效电路模型，本文在0.1～40 GHz 的频率范围内对其进行频域仿真，并提取相应的回波损耗S11和插入损耗S21.为验证等效电路模型的准确性，同时采用全波电磁仿真软件Ansys HFSS 对1S4G MD CSTSV 结构进行全波仿真以得到相应S参数结果.基于两种方法（相关结构尺寸沿用表1 中的尺寸数据）得到的S 参数的对比结果在图7 中给出.从图7 中可以看出,在仿真的频率范围内，基于提取的单位长度RLGC 电学参数所构建的等效电路模型的S参数仿真计算结果与通过HFSS 全波仿真得到的S参数结果之间的匹配较好，最大误差不超过7%.该对比结果表明了在当前结构尺寸下，将1S4G MD CSTSV 结构的比例因子λ视为1 以用于单位长度RLGC 电学参数的提取并建立相应的等效电路模型是可行且准确的.考虑到在MD CSTSV 结构的单位长度G、C电学参数的提取过程中是通过引入比例因子λ 的环形介质层的复电容的计算公式去求得的近似解，这应该是造成上述等效电路模型仿真计算与基于HFSS 全波仿真得到的S参数结果之间的误差的主要原因.

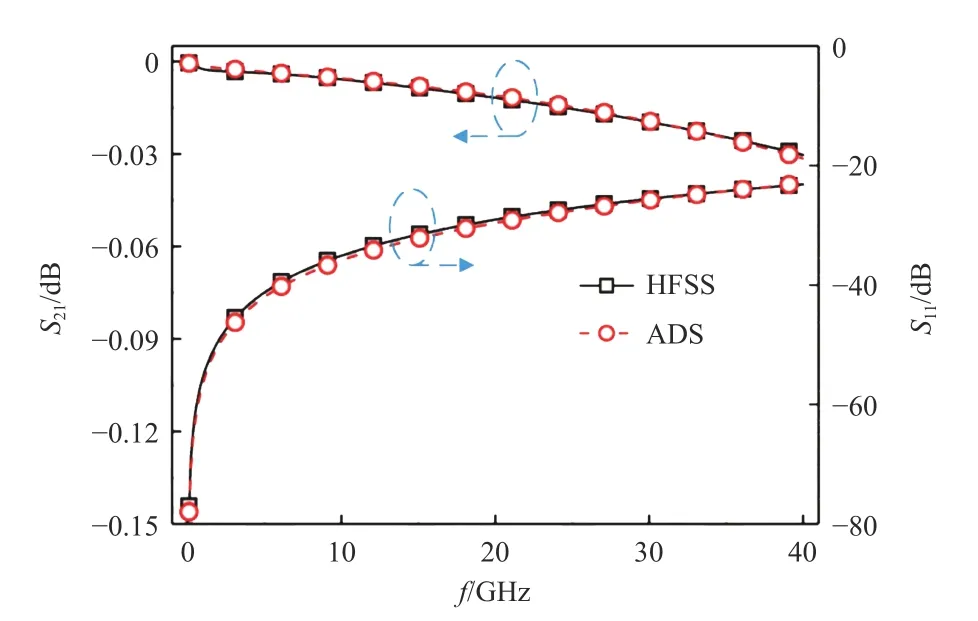
图7 1S4G MD CSTSV S 参数仿真结果Fig.7 Simulation results of 1S4G MD S parameters

为进一步确认引入比例因子λ的可行性以及所提取的单位长度RLGC 电学参数和所建立的等效电路模型的准确性，本文基于表4 给出的具有不同结构参数的MD CSTSV 进行仿真验证，相应的仿真结果如图8 所示.针对两个具有不同混合介质层厚度尺寸的1S4G MD CSTSV 结构，图8 (a)和图8 (b)分别给出它们各自通过等效电路模型仿真计算与基于HFSS 全波仿真得到的S参数结果.对于这两个1S4G MD CSTSV 结构，在0.1～40 GHz 的频率范围内，基于两种仿真方法求得的S参数结果之间的最大误差均不超过7%，这表明对于具有不同结构尺寸的MD CSTSV 结构，将1S4G MD CSTSV 结构的比例因子λ视为1，并进行相应的单位长度RLGC 电学参数提取依旧是可行的，且相应的单位长度RLGC 电学参数和等效电路模型是准确的.图8(c)和图8 (d)则分别给出了1S6G MD CSTSV 结构与1S8G MD CSTSV 结构（相关结构尺寸与图8 (a)所对应的1S4G MD CSTSV 结构一致）通过等效电路模型仿真计算与基于HFSS 全波仿真得到的S参数结果.同样的，在0.1～40 GHz 的频率范围内，对于这两个具有不同接地TSV数量的MD CSTSV 结构，它们各自基于两种方法求得的S参数结果之间的最大误差也是不超过7%，这表明以1S4G MD CSTSV 结构作为基准来计算具有不同接地TSV 数量的MD CSTSV 结构的比例因子λ并进行相应的单位长度RLGC 电学参数提取和等效电路模型建立同样是可行的，且准确性较高.

表4 具有不同结构参数的 MD CSTSV (不同结构尺寸或接地 TSV 数量)Tab.4 MD CSTSV with different structural parameters (different structural dimensions or number of grounded TSV)

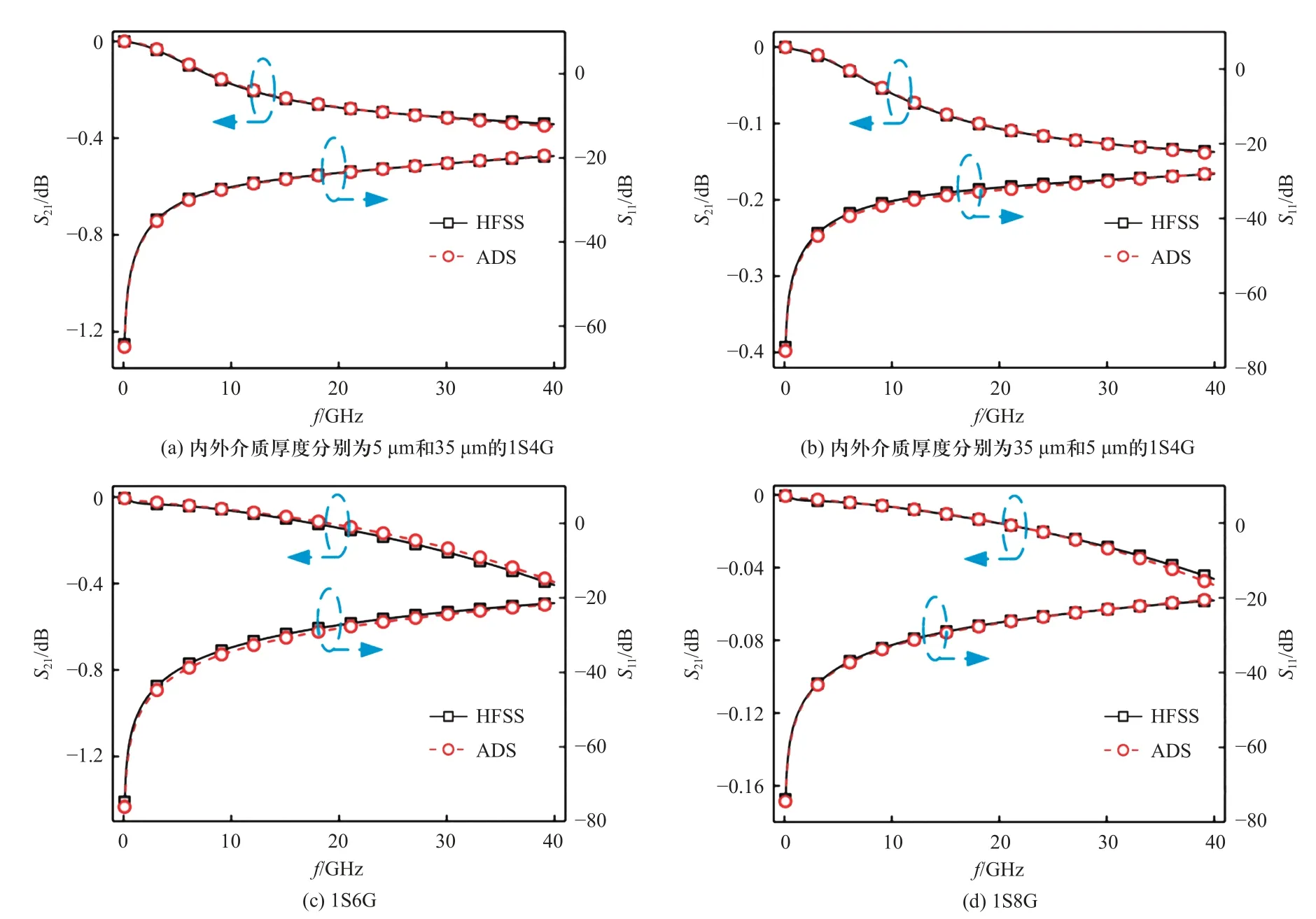
图8 具有不同结构参数的 MD CSTSV 的等效电路模型验证结果Fig.8 Verification results of MD CSTSV equivalent curcuit model with different structural parameters

3 结 论

本文针对MD CSTSV 结构, 利用多导体传输线理论和引入比例因子λ的环形介质层的复电容的计算公式分别提取了其单位长度等效R、L电学参数和单位长度近似G、C电学参数，并建立了相应的等效电路模型.在0.1～40 GHz 的频率范围内，通过等效电路模型仿真计算与基于HFSS 全波仿真得到的S参数结果之间的最大误差小于7%.因此，基于本文提出的求解方法所提取的单位长度RLGC 电学参数及相对应的等效电路模型可以准确地模拟MD CSTSV 结构的传输特性.