恐怖袭击下地铁隧道结构爆炸响应与防护对策

高金金，郭盼盼，马晶晶，汪亦显

（1.中国工程院战略咨询中心，北京 100088；2.合肥工业大学 土木与水利工程学院，安徽，合肥 230009；3.合肥市轨道交通集团有限公司，安徽，合肥 230601）

自世界上第一条地铁−伦敦大都会铁路于1863 年开通以来，地铁作为城市公共交通的重要组成部分，在缓解城市地面交通压力、促进经济社会发展方面发挥着不可替代的作用.截至目前，我国城市地铁运营总里程已超过8 000 km，稳居世界首位.然而，由于极端自然灾害、技术缺陷、恐怖主义等不可避免因素的存在，地铁的安全运营也面临着诸多威胁.其中，爆炸恐怖袭击由于破坏和杀伤力大、易发动、难防范等特点[1]，已成为地铁安全运营面临的最严重的威胁之一，极易造成巨大的人员伤亡和经济财产损失（表1），逐渐引起世界各国的高度重视.

表1 典型的地铁爆炸恐怖袭击事件Tab.1 Typical terrorist bombing attacks in metros

地铁爆炸恐怖袭击的防护是一项系统工程，涉及风险预测、后果评估、灾害预报、应急响应、风险应对、处治技术措施等多个方面[2].其中，爆炸冲击波荷载下隧道结构的安全可靠是保证地铁内部安全的基础和前提[3]，可以有效避免结构破坏带来更大的二次伤害和保障救援工作的开展.爆炸冲击波荷载下地铁隧道结构的力学响应是判断其是否处于安全状态的直接依据.因此，研究地铁隧道结构的爆炸响应及基于爆炸响应的防护措施对于有效减轻突发爆炸造成的破坏、伤亡和经济财产损失，并保证地铁安全运营具有重要意义.

隧道结构的爆炸响应是一个涉及到爆炸力学、损伤力学、流体动力学、结构动力学、波动理论等多学科交叉、多场耦合的复杂课题.目前，关于该课题国内外已取得了一定的研究进展.已有研究表明[4]，隧道结构爆炸响应与多种因素有关，例如爆炸当量、炸药与隧道结构的相隔距离、隧道埋深、炸药位置、隧道截面形状、隧道衬砌及其周围岩土体的物理力学特性.爆炸当量对隧道结构的影响研究所关注的响应参数主要包括隧道结构的位移[5]、压力[6]、应力[7]、应变[8]、加速度[9]、速度[10]等.PRASANNA 和BOOMINATHAN（2014）[11]的研究表明，随着炸药与隧道结构相隔距离的增大，作用于隧道结构上的外部爆炸压力强度减小，结构损伤减小.YU 等（2016）[12]指出，随着隧道埋深从6 m 增加到12 m，在内爆作用下圆形隧道拱顶处的有效塑性应变减小.FELDGUN 等（2014）[13]研究了矩形隧道在靠近地面的中心爆炸和偏心爆炸作用下壁面的压力分布，结果表明隧道衬砌在偏心爆炸作用下的最大峰值压力高于中心爆炸作用下的峰值压力.MOBARAKI 和VAGHEFI（2015）[14]研究发现，与圆形、箱形和拱形截面的隧道相比，半椭圆隧道由于其土体与隧道的接触区域最大，在相同的外部爆炸作用下，其损伤最小.现有关于衬砌材料性能对隧道爆炸响应影响的研究主要集中在衬砌刚度、强度、阻尼、脆性、厚度、衬砌材料类型、管片接头类型、管片数量等参数的影响上[15−19].隧道衬砌周围岩土体物理力学特性对隧道结构爆炸响应的影响研究所考虑的参数主要集中于岩土介质含水量、强度、刚度、密度、阻尼系数、波阻抗、侧压力系数等[20−25].

然而上述研究主要是针对公路隧道开展的，而对地铁隧道的关注略显不足.在实际工程中，常用的地铁隧道结构可分为两大类：一类是整体现浇钢筋混凝土结构；另一类是管片拼装结构.管片拼装隧道在盾构法施工方法中应用较多，其结构是由管片通过环向和纵向螺栓接头拼装而成.管片接头位置及类型对爆炸响应有重要影响，因此采用管片拼装的地铁隧道结构的爆炸响应比公路隧道中常见的整体现浇隧道结构的爆炸响应更加复杂[26].ZHAO 等（2016）[27]基于试验研究发现，在内爆炸荷载作用下，隧道管片接头处由于应力集中现象更容易发生开裂.KONESHWARAN（2014）[28]指出，对于低爆炸荷载，管片接头类型通过允许管片发生旋转的方式影响隧道结构响应，而对于高爆炸荷载，管片接头的转动效应无法发挥.王鹏飞（2022）[29]采用有限元法分析了管廊燃气舱内燃气爆炸对邻近地铁隧道动力响应的影响，揭示了埋置深度、天顶距、空间角度的影响效应.然而，地铁隧道爆炸响应的研究手段、结构动力响应、毁伤效应及防护对策还未得到充分研究.此外，目前也未见有关地铁隧道结构爆炸响应及防护研究现状的总结与展望，从而在一定程度上阻碍了地铁隧道防爆理论及防爆实践的发展与进步.

为进一步促进地铁隧道防爆设计理论及技术的发展与进步，本文综述了爆炸冲击波荷载下地铁隧道结构响应的最新进展，并展望了值得重视的未来发展及研究方向.研究成果对于地铁隧道防爆技术的研究与实践具有积极意义.

1 地铁隧道爆炸响应研究手段

1.1 足尺试验

足尺试验能够反映原型的真实结构尺寸特征，因此其结果最为可靠.足尺试验结果不仅可以揭示地铁隧道结构的真实爆炸响应及其机理，而且可为验证理论解和数值模型提供重要的数据支撑.然而，足尺试验具有成本高、周期长、可控性差、操作复杂、对专业技术要求高等缺点，因此基于足尺试验手段的地铁隧道结构爆炸响应研究十分稀少.

为研究中心装药和偏心装药2 种工况下的地铁隧道结构的爆炸响应，ZHAO 等（2016）[27]开展了2 组足尺试验，如图1 所示.在该试验中，竖直埋入土体中的地铁隧道结构均由四环衬砌组成（总长4.8 m），每环衬砌包括3 块A类管片、2 块B类管片、1 块K类管片.管片厚度为0.4 m，宽度为1.2 m，衬砌结构内径、外径分别为5.5 m、6.3 m.最大装药质量为20 kg（TNT 当量），起爆采用中心点燃法，炸药中心与隧道结构内表面的最小距离为0.8 m.偏心装药工况中（图1(d)），炸药位置根据南京地铁车厢几何特征的最不利条件确定.应变片贴在距离炸药最近和最远位置处的管片接头螺栓表面，以测量螺栓的塑性变形.

图1 地铁隧道结构爆炸响应足尺试验照片及示意图[27]Fig.1 Photograph and schematic diagram of full-scale tests on blasting response of metro tunnel structure[27]

足尺试验结果表明：①在中心装药和偏心装药爆炸冲击波荷载作用下，隧道管片结构的破坏主要集中在离炸药最近的管片接头区域，炸药所在的衬砌环的破坏最严重；② 在内爆炸冲击波荷载作用下，由于环向螺栓对管片外移的约束作用，应力集中现象发生于管片接头接触区；③ 管片主要发生径向扩张，而沿隧道轴线方向上的位移较小；④ 在偏心装药爆炸冲击波荷载作用下，隧道衬砌环的整体变形呈现椭圆形模式.

基于上述试验结果，可以发现该足尺试验方法考虑了地铁隧道结构的典型关键特征，例如管片接头、管片错缝拼装方式、管片尺寸、炸药位置等，因此基本上能够揭示出地铁隧道结构在内爆炸冲击波荷载下的典型破坏模式机理.然而，该方法存在几点主要缺陷：①作用于管片外壁上的土压力量值及其分布无法真实反映；② 没有考虑地铁车厢对爆炸冲击波传播与反射的影响效应；③竖直埋入土体中的地铁隧道结构的爆炸响应与实际工况存在一定差异；④有限长度下的边界效应对试验结果的影响无法消除.

1.2 理论解析法

理论解析法是进行地铁隧道结构抗爆分析、爆炸损伤评估和防护设计的重要手段.然而，目前关于地铁隧道结构爆炸响应方面的理论解析法极少[30−31]，这主要是由于：① 管片接头对隧道结构爆炸响应的影响很难在理论解析法中模拟；② 爆炸冲击波荷载的量值及加载速率极高，很难等效为静力荷载，且惯性力在瞬态分析中不可忽略.

LIU 等（2014）[30]基于土−结构动力相互作用的集中质量模型，提出了一种地表爆炸荷载作用下地铁隧道结构动力弹塑性分析的简化计算方法.该方法将管片简化为刚体，将管片接头简化为弹塑性铰，将周围土体视为黏弹性地基.根据该方法，单块管片的平动、转动位移满足的微分方程的最终形式为：

式中：xi(t)、yi(t)、θi(t)分别为管片水平位移、竖向位移、转角；mi为管片质量；t为起爆后的任意时刻；pxi(t)、pyi(t)分别为传递至管片外表面的爆炸荷载在x、y方向的投影；Mpi(t)为合力矩；Fki、Fki+1分别为当前位置处和下一位置处纵向管片间的相互作用力；F0为螺栓预加荷载；θsi为管片上某点相对于水平方向的夹角；θci为管片两端截面之间的夹角；fi、fi+1分别为当前位置处和下一位置处管片表面的滑动摩擦力；Qi、Qi+1分别为当前位置处和下一位置处管片与螺栓之间的作用力；Mi、Mi+1分别为管片两端面上作用的弯矩；Ii为管片的质量惯性矩；R0为管片半径.

该方法[30]能够考虑爆炸冲击波荷载下管片与接头螺栓间、管片与周围岩土体间的相互作用，同时也能反映围岩等级及接头刚度对地铁隧道结构爆炸响应的影响效应.然而，由于该方法不考虑管片变形（即将管片简化为刚体），因此高估了爆炸冲击波荷载下管片的最大速度和接头的最大水平位移.此外，该方法仅适用于爆炸源位于地铁隧道轴线对应的地表位置处的工况，因此其实用性有限.

HU 等（2018）[31]提出了一种统计等效连续薄壳模型，用于预测轴对称内爆炸荷载作用下的地铁隧道结构的动力响应.在该模型中，土体的作用采用仅抗压的单向线弹性文克勒土弹簧和波阻抗模拟，爆炸荷载采用经典的简化模型描述，方程求解采用欧拉显式法.该模型能够考虑管片接头对隧道结构整体刚度的弱化效应，且可给出接头位置处的应力集中量和应变集中量.然而该方法仅适用于内爆炸荷载为轴对称的工况.此外，由于该方法忽略了接头螺栓惯性作用，因此其精度有待进一步验证.

此外，上述两种理论解析法存在的最大的问题是没有考虑结构的失效.事实上，爆炸冲击荷载作用下隧道结构大多以失效破坏为主，较少数仅存在弹塑性变形.

1.3 数值模拟

与足尺试验、理论解析法相比，数值模拟在地铁隧道结构爆炸响应研究中的应用更加广泛.数值模拟克服了足尺试验的成本高、危险性大的缺点，解决了理论解析法难以考虑的管片接头效应的模拟问题，且能够考虑炸药、空气、结构与土体之间的完全耦合效应.地铁隧道结构爆炸响应的数值模拟研究涉及的技术问题主要包括：爆炸冲击波荷载的模拟；管片接头效应的考虑与模拟；材料模型、状态方程及其参数的确定.

1.3.1 爆炸冲击波荷载的模拟

常用的爆炸冲击波荷载的模拟方法主要包括：① 采用作用在地铁隧道结构内表面上的超压时程曲线经验函数描述爆炸冲击波荷载（简称经验法）[32−33]；②基于流固耦合算法模拟炸药爆炸过程及其产生的空气冲击波对隧道结构的作用效应（简称流固耦合 法）[34−38]；③使 用LOAD_BLAST 或LOAD_SEGMENT 关键字对地铁隧道结构内表面施加爆炸荷载（简称关键字法）[39−44].

经验法将爆炸荷载简化为一个随时间变化的节点力施加到地铁隧道结构上，可以大大节约计算资源.炸药起爆后，爆炸冲击波传播过程中会发生入射、透射、反射、绕射等现象，导致作用在结构表面的超压随时间呈振荡衰减趋势（如图2(a)）.李忠献等（2006）[32]将超压时程曲线进一步简化（如图2(b)），并基于此开展数值分析，得到的衬砌应力时程曲线与已有试验结果吻合较好.单生彪等（2016）[33]采用的超压时程曲线（图3）仅有一个峰值，可用指数型的时间滞后函数表示，给数值计算带来了极大便利，但与呈振荡衰减趋势的超压时程曲线差别较大.然而，经验法无法真实反映超压荷载在复杂结构表面上的空间分布特性及其随时间的变化规律，也无法考虑爆轰产物及碎片对结构的侵彻作用，其计算精度无法保证，因此仅适用于定性分析.

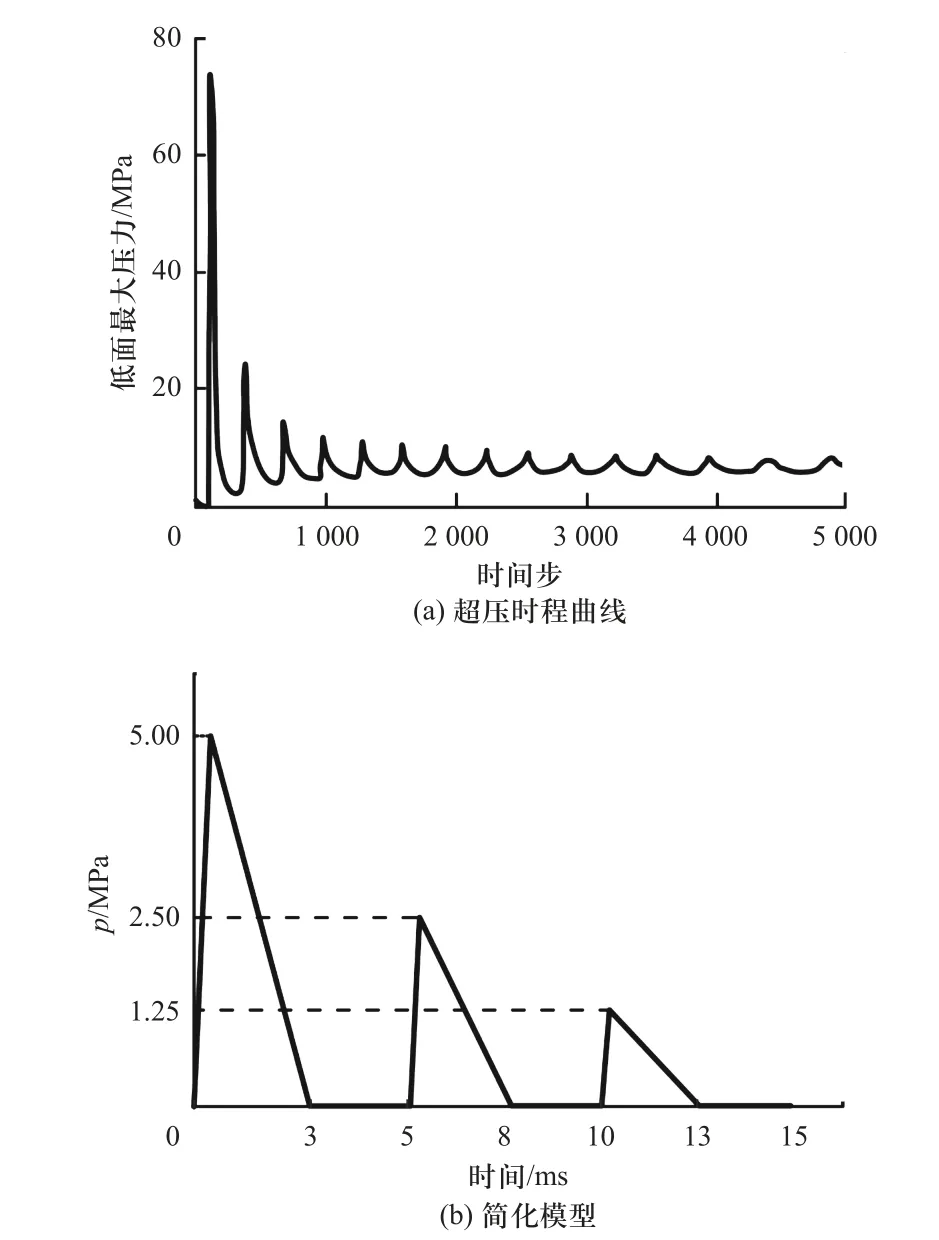
图2 超压时程曲线及其简化模型[32]Fig.2 Overpressure time history curve and its simplified model [32]

图3 炸药爆炸后0.1 s 内的时程荷载函数曲线[33]Fig.3 Time history load function curve within 0.1 s after explosive explosion [33]

流固耦合法通过建立“炸药−空气−(土体)结构”耦合模型，将爆炸产生的冲击波超压荷载以接触爆炸、流固耦合、共用节点等方式施加到隧道结构上，可以较为准确地模拟炸药爆炸产生的冲击波在介质中的传播过程及其对结构物的作用效应.然而，该方法所需的计算单元数量巨大，计算成本很高，也无法考虑爆轰产物及碎片对结构的侵彻作用.该方法适用于研究冲击波绕流、反射等作用对结构影响较大的地铁结构内爆炸响应问题.

关键字法通过定义装药量、引爆位置、起爆方式、起爆时间、模型迎爆面等参数模拟施加在结构上的爆炸荷载，因此不需建立炸药网格、空气网格，避免了繁琐复杂的ALE 耦合分析和欧拉计算过程，因此大大提高了计算效率.但该法不能考虑应力波叠加和冲击波绕射对隧道结构爆炸响应的影响，也无法考虑爆轰产物及碎片对结构的侵彻作用，因此适用于结构、受力简单且不考虑应力波叠加和冲击波绕射作用效果的计算问题.关键字法中的爆炸荷载P(t)可表达为

式中：Pr0、Ps0为反射、入射超压峰值；t为起爆后任意时刻；t0为正压作用时间；a、b分别为反射、入射压力衰减系数；θ为爆炸入射角.

1.3.2 管片接头效应的考虑与模拟

管片接头是影响地铁隧道结构爆炸响应的最重要的因素，也是使地铁隧道结构抗爆性能区别于整体现浇隧道结构抗爆性能的关键.因此，地铁隧道结构爆炸响应的研究应当着重考虑管片接头效应.然而，在一些地铁隧道结构爆炸响应的数值模拟研究中，隧道结构直接被简化为连续的圆筒状结构[45−50]（图4(a)），或者管片之间采用面面固连接触[51−52]，这种操作忽视了地铁隧道结构的典型特征，无法揭示地铁隧道结构在爆炸冲击波荷载作用下的破坏特征和灾变机制，因此其研究成果仅适用于整体现浇隧道结构.

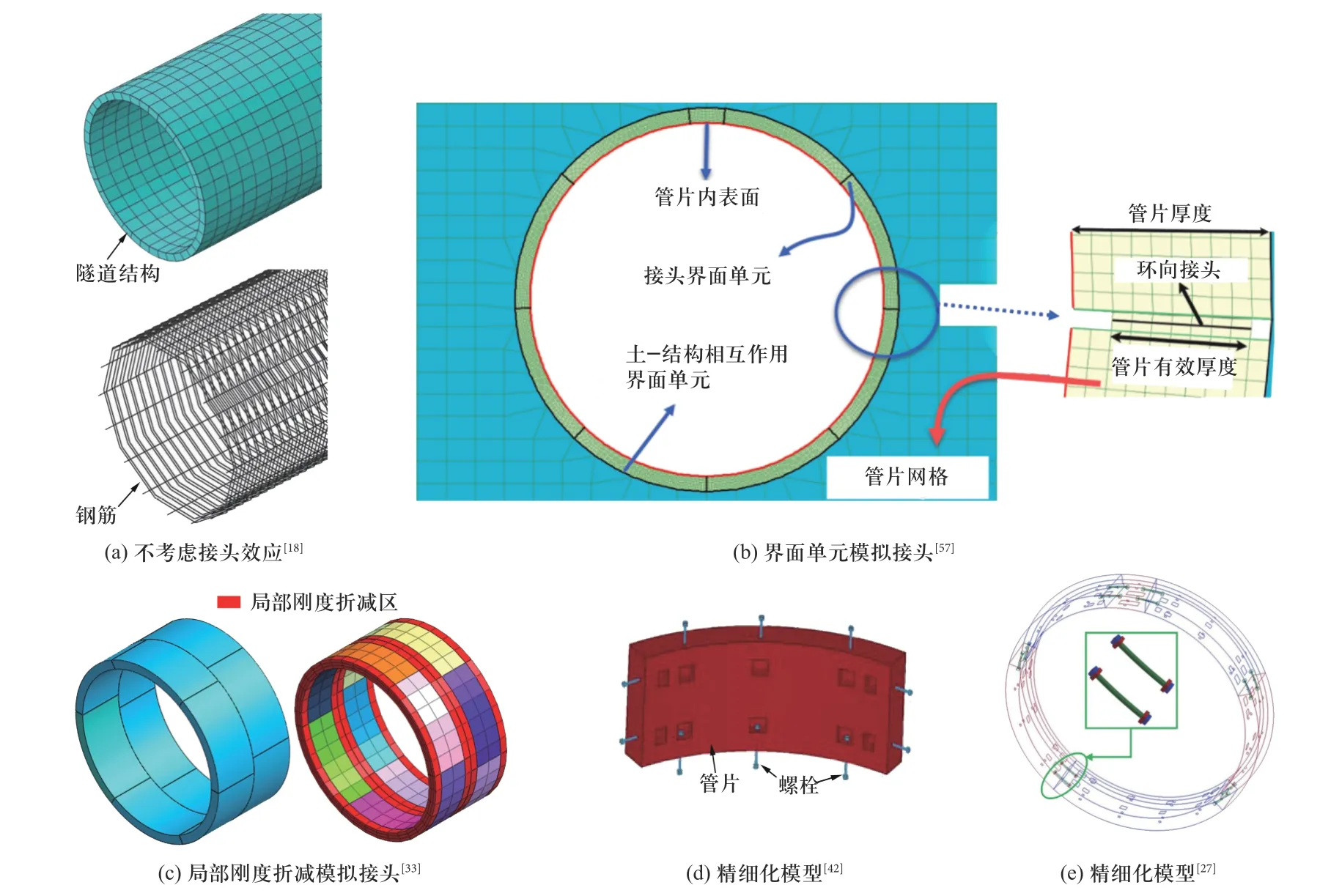
图4 管片接头效应模拟方法Fig.4 Method for simulating segment joint effect

管片接头效应的模拟方法主要包括：① 建立考虑管片与周围土体、管片与管片、管片与接头螺栓界面接触效应的精细化三维有限元模型[26,28,39,41−42,53−54]（图4(d)、4(e)）；② 采用刚度折减后的钢筋混凝土结构模拟管片接头[33]；③ 采用剪切弹簧和非线性扭曲弹簧模拟管片接头纵向、环向螺栓[55−56]（图4(c)）；④ 采用界面单元模拟管片接头的接触和转动行为[57]（图4(b)）.其中，考虑各种接触效应的精细化三维有限元模型尽管单元数量较多、计算成本较高，但能够反映出爆炸冲击波荷载下地铁隧道结构纵向接头的错台和环向接头的张开，且能够揭示管片接头螺栓的变形和破坏机理，因此其计算结果的精度更高，适用于重要工程的抗爆分析与优化设计.

1.3.3 材料模型、状态方程及其参数确定

选择合适的材料模型、状态方程及其参数是保证数值模拟结果有效性的基础.地铁隧道结构爆炸响应数值模拟研究中涉及的材料主要包括炸药、空气、土体、管片衬砌结构（包含混凝土、钢筋及接头螺栓）.表2 总结了LS-DYNA 模拟炸药、空气、土体及结构时常用的本构模型及炸药、空气的状态方程.

表2 LS-DYNA 模拟地铁隧道爆炸响应时采用的本构模型及状态方程Tab.2 Constitutive models and state equations used for simulating metro blasting using LS-DYNA

在LS-DYNA 中，高爆炸药材料模型与JWL 状态方程相结合以模拟一定当量炸药爆炸释放化学能量并在周围介质中形成爆炸冲击波压力的过程.JWL状态方程的6 个参数可基于使程序模拟结果逼近圆筒试验结果得到.空气采用空材料模型描述，空材料模型与线性多项式状态方程联合以模拟炸药爆炸产物流动的空腔.土体常用MAT_SOIL_AND_FOAM 模型模拟，该模型包含密度、弹性模量、泊松比、内摩擦角、黏聚力5 个参数.模拟混凝土材料的HJC 模型可综合考虑材料的高压效应、高应变率和大应变.随动硬化塑性模型可用于模拟混凝土和螺栓，当与MAT_ADD_EROSION 关键字联合使用时，可反映接头螺栓的断裂破坏形态.Winfrith 模型是基于OTTOSEN（1977）[58]提出的剪切破坏面建立起来的，通过嵌入裂缝宽度或断裂能，可以考虑应变率效应以及拉伸应变软化.

2 地铁隧道结构动力响应及毁伤效应

2.1 运动响应

2.1.1 位移

爆炸冲击波荷载下地铁隧道结构的位移响应受多种因素影响，包括接头模拟方法、炸药位置、炸药当量、爆心距离等.基于刚度折减法，单生彪等（2016）[33]采用Midas/GTS 有限元软件研究了接头模拟方法对内爆炸荷载下地铁隧道结构竖向位移和横向位移的影响效应，如图5 所示；其中“竖向”、“横向”以及后文涉及到的“径向”与“轴向”的定义如图6 所示.研究发现，竖向和横向位移均在起爆后0.015 s 时刻附近达到峰值，随后逐渐衰减，其原因主要为所施加的爆炸荷载在0.01 s 之前达到峰值，随后迅速衰减；刚度局部折减时的位移量值是刚度整体折减和不折减时的2 倍以上.可见，管片接头的存在使地铁隧道结构的位移响应更大.

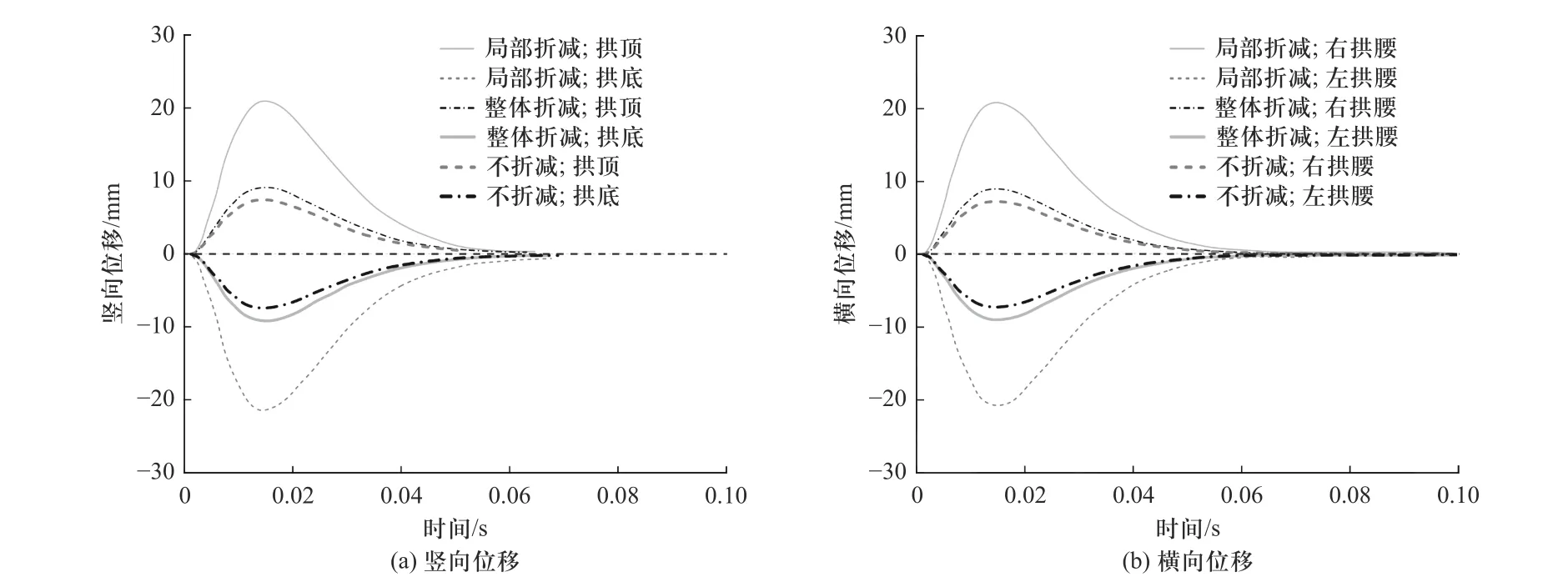
图5 基于刚度折减法的爆炸冲击波荷载下隧道结构典型位置位移响应[33]Fig.5 Stiffness-reduction-method based displacement response at typical locations of tunnel structure subject to blasting[33]

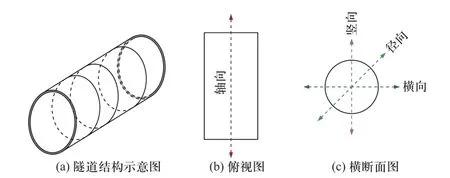
图6 隧道运动响应分析中所涉及方向示意图Fig.6 Schematic diagram of directions involved in analysis of tunnel motion response

管片接头对位移响应的影响如图7 所示.在20 kg TNT 偏心（距隧道底部1.1 m）爆炸荷载作用下，盾构隧道结构在接头部位发生了错动，且其最大径向位移量是整体隧道结构的2.79 倍.此外，盾构隧道管片环与环之间的错动随装药量增大、与爆心断面距离减小而增大；随着与爆心断面距离的增大，盾构隧道底部的竖向位移峰值的衰减速度大于整体隧道结构，当与爆心断面的距离增大至3 环管片宽度时，盾构隧道结构底部内表面的竖向位移峰值开始小于整体隧道结构.

图7 爆心断面隧道衬砌结构径向位移峰值示意图（单位：mm）[42]Fig.7 Schematic diagram of peak radial displacement of tunnel structure at detonation section (unit: mm)[42]

炸药位置及当量对地铁隧道结构位移响应有显著影响.当炸药位于地表时，与侧爆角度为30°、45°的工况相比，侧爆角度为15°的工况对应的地铁隧道结构的横向位移最大，隧道结构的径向位移随着侧爆角度增大而迅速衰减[45].当炸药位于隧道内部时，距隧道衬砌底部1.1 m 处的10 kg TNT 当量的炸药爆炸导致的结构最大竖向位移为8.5 mm[50]；然而，在田志敏等（2011）[44]的研究中（图8），距隧道衬砌底部1.1 m 处的40 kg TNT 当量的炸药爆炸导致的结构最大竖向位移仅为5.1 mm，这主要是由衬砌厚度不同造成的（前者为0.30 m，后者为0.65 m）.当炸药位置保持不变时（距结构底部1.1 m 处），爆炸当量由40 kg增大至220 kg 导致最大竖向位移由5.1 mm 增大至22.8 mm.当爆炸当量保持为220 kg 时，炸药距离隧道结构底部1.1、0.5、0 m 下的隧道结构底部最大位移分别为22.8、282、333 mm.可见，炸药与隧道结构底部的距离越小，隧道结构的位移响应越明显.

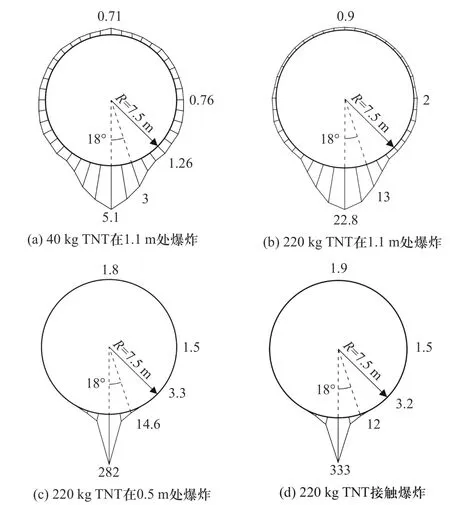
图8 爆心断面隧道径向位移峰值示意图（单位：mm）[44]Fig.8 Schematic diagram of peak radial displacement of tunnel at detonation section (unit: mm)[44]

2.1.2 速度及加速度

爆炸冲击波荷载下地铁隧道结构的速度及加速度响应主要受接头模型、炸药当量、炸药位置三种因素的影响.如图9 所示，当采用局部折减、整体折减、不折减接头模型时，隧道拱顶竖向速度峰值和右拱腰横向速度峰值均分别为2.8、1.2、0.9 m/s，拱底竖向速度峰值和左拱腰横向速度峰值均分别为−2.8、−1.2、−0.9 m/s，而两拱腰处的竖向速度以及拱底、拱顶处的横向速度均几乎为0.可见，地铁隧道结构不同位置处的速度响应在空间上呈上下及左右对称模式，其内在机制为荷载及结构对称导致的速度响应对称.隧道结构的速度响应除了具有空间效应外，也具有时间效应，其具体表现为：在采用3 种接头模型的工况中，随着爆炸时间的推进，隧道拱顶、拱底处的竖向速度及左拱腰、右拱腰处的横向速度均呈波峰逐渐衰减的波浪型演化；竖向及横向速度的第一个峰值均约发生于0.005 s 时刻，第二个峰值均约发生于0.025 s 时刻，随后逐渐衰减至0；竖向及横向速度的第二个峰值约为其第一个峰值的1/2，但方向是相反的，表明爆炸能量在隧道结构中的耗散速率较大.此外，采用不同接头模型时的隧道结构速度响应规律的对比表明，管片接头的存在使得爆炸冲击波荷载下地铁盾构隧道结构的速度响应大于整体式隧道，其主要原因是接头降低了隧道结构的整体性和刚度，从而更容易发生径向扩张变形.

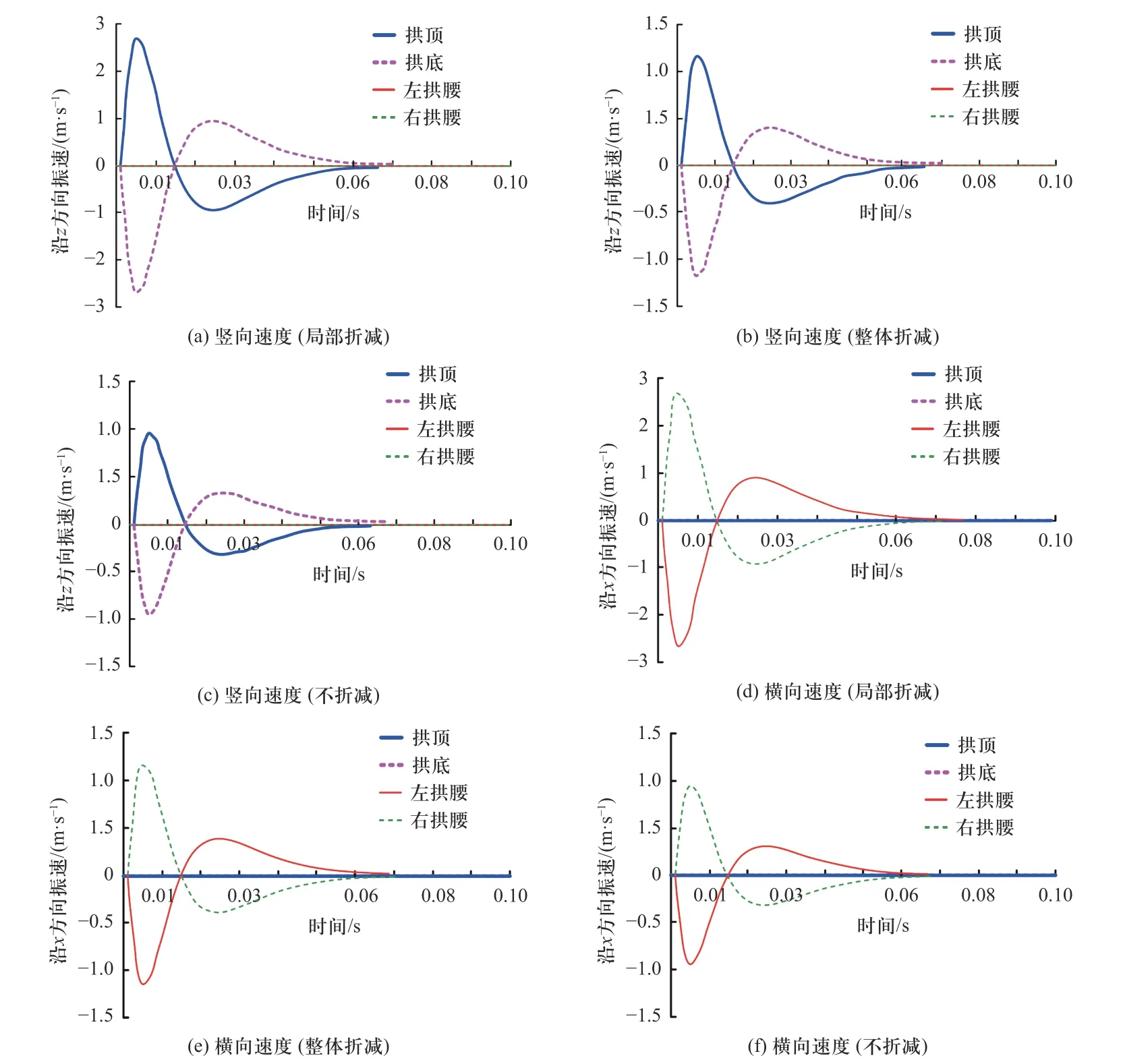
图9 接头模型对地铁隧道结构速度响应的影响[33]Fig.9 Influence of joint model on velocity response of metro tunnel structure[33]

炸药当量对地铁隧道结构速度响应的影响如图10 所示，其中炸药位于地表，侧爆角度为15°，隧道轴线埋深为15 m.由图可见，随着炸药当量的增大，拱顶竖向位移及左侧帮横向位移近似呈线性增加，且左侧帮横向速度的增速略大于拱顶竖向位移的增速；同一炸药当量下，左侧帮横向速度大于拱顶竖向速度.当炸药位于隧道正上方地表时[39]，100 kg 炸药当量下隧道拱顶和拱腰处的峰值加速度分别为357、−231 m/s2，300 kg 炸药当量下隧道拱顶和拱腰处的峰值加速度分别为672、317 m/s2.可见，炸药当量增大不仅提高了隧道结构的峰值加速度，而且改变了隧道结构拱腰处峰值加速度的方向.

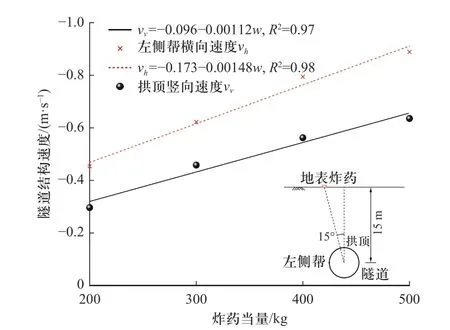
图10 炸药当量对地铁隧道结构速度响应的影响[45]Fig.10 Influence of explosive equivalent on velocity response of metro tunnel structure[45]

炸药可能位于地表、地层内部或隧道内部，当炸药位置固定时，地铁隧道结构不同部位具有不同的速度和加速度响应.针对10 kg TNT 当量炸药在距隧道结构底部1.1 m 处爆炸时的工况，图11 给出了爆心断面、距爆心4 m 处断面、距爆心8 m 处断面上隧道结构沿着横向和竖向的最大速度和最大加速度.由图可见，随着与爆心断面距离的增大，隧道结构横向和竖向的最大速度和最大加速度均不断减小.此外，炸药位置对隧道结构速度峰值出现的时间也有影响.例如，炸药位于隧道结构截面几何中心工况下结构竖向速度峰值出现的时间晚于炸药位于行车道板中部上缘工况下结构竖向速度峰值出现的时间[51].

2.2 内力响应

在爆炸冲击波荷载作用下，地铁隧道结构的内力响应包括管片内力响应和接头螺栓内力响应两层含义.当采用局部刚度折减法、整体刚度折减法、不折减法模拟管片接头效应时，管片在起爆后0.014 s的最大主应力云图如图12 所示[33].由图可见，局部折减时接头部位发生了明显的应力集中现象，且其最大主应力的量值大于整体折减和不折减时的最大主应力量值，表明地铁隧道结构接头部位是内力响应的薄弱部位，应重点关注；管片内壁上的最大主应力明显大于外壁上的最大主应力，这是由爆炸应力波向远处扩散过程中不断衰减造成的.

图12 不同接头模型工况下起爆后0.014s 时隧道结构最大主应力云图[33]Fig.12 Contours of maximum principal stress of tunnel structure at 0.014s after detonation under different joint model conditions [33]

在40 kg TNT 装药位于距隧道底部1.1 m 爆高处爆炸产生的冲击荷载作用下，地铁隧道结构接头螺栓的最大、最小主应力响应如图13 所示.可以看出，环向螺栓与纵向螺栓具有明显不同的受力状态.如图13(a)所示，环向螺栓（8.8 级M30）的最大、最小主应力为正值，表明其主要承受拉应力，其最大主应力在0.0015 s 时刻附近达到峰值700 MPa，超过了抗拉极限强度，因此发生了断裂破坏而丧失抗拉能力，最大、最小主应力降为0.如图13(b)所示，纵向螺栓（8.8 级M30）的最大主应力为正值，其峰值明显小于环向螺栓的最大主应力峰值，其最小主应力有正也有负，表明纵向螺栓既承受拉应力也承受压应力，但没发生断裂破坏.此外，螺栓的延性及强度也对地铁隧道结构的抗爆性能有重要影响.

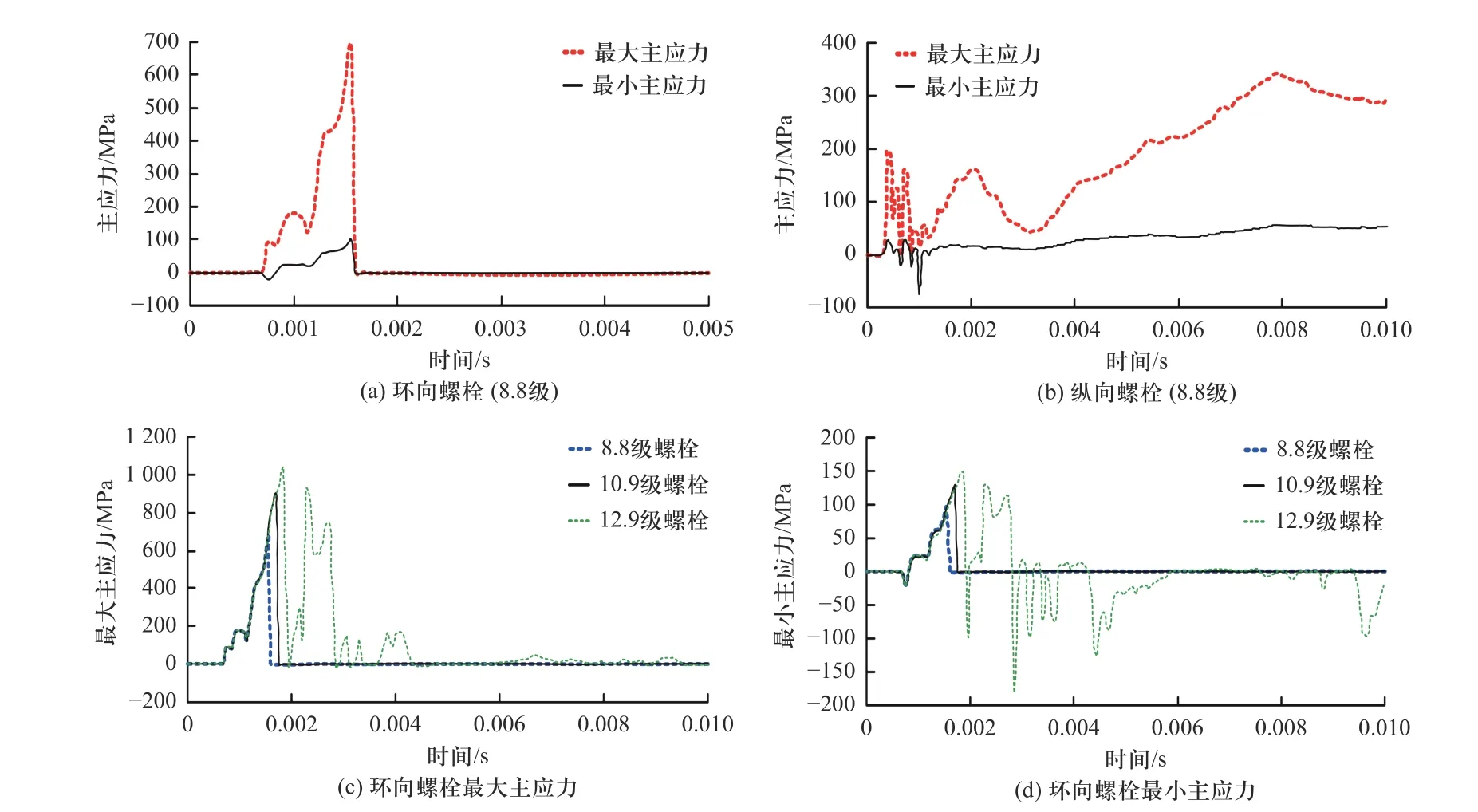
图13 地铁隧道结构接头螺栓主应力时程曲线[42]Fig.13 Principal stress time history curve of metro tunnel structural joint bolts[42]

图13(c)、13(d)分别对比了8.8、10.9、12.9 级环向螺栓的最大、最小主应力时程曲线.可见，8.8 和10.9 级螺栓均在0.002 s 前发生了拉断破坏，而12.9级螺栓未发生拉断破坏，表明接头螺栓的强度越高，盾构隧道的整体抗爆性能越强.此外，由图13(d)可见，12.9 级螺栓的最小主应力既有正值也有负值，不同于8.8 级螺栓的最小主应力仅为正值（图13(a)），表明环向螺栓的受力模式由8.8 级的纯受拉状态转变为12.9 级时的受拉受压组合状态.因此，提高螺栓强度也能改善环向螺栓的受力状态，从而降低了发生拉断破坏的风险.

2.3 破坏特征

爆炸冲击波荷载作用下，地铁隧道结构的破坏特征与管片力学参数、尺寸及拼装方式、爆炸当量、起爆位置、地层特性等多种因素相关.针对软土地层中采用通缝拼装方式的地铁区间隧道，邬玉斌（2011）[26]采用有限元法分析了该隧道管片及其连接螺栓在不同质量TNT 装药距隧道底部1.1 m 处爆炸时的破坏特征，如图14 所示.当TNT 装药量为20 kg 时，爆炸近区的隧道结构发生环缝开裂、纵缝错台的破坏特征（图14(a)），该特征表明管片接头是地铁隧道结构受到爆炸冲击波荷载作用时的最薄弱部位，其典型的破坏特征为环向接头张开、纵向接头错动.管片纵向接头错动量随装药量增加而逐渐增大，当装药量增大到一定程度之后（例如220 kg），位于隧道顶部的封顶块因管片纵向接头错动量过大可能会脱离于其他管片（图14(b)），从而可能造成严重的坍塌现象.爆炸冲击波荷载作用下，管片接头的张开或错动受到连接螺栓的限制作用，因此连接螺栓也会发生变形甚至破坏.当TNT 装药量为40 kg 时，如图14(c)所示，管片环向接头的张开导致环向螺栓发生拉断，管片纵向接头的错动导致纵向螺栓发生弯曲变形.当TNT 装药量增大至220 kg 时，纵向螺栓因管片纵向接头的错动量过大而同样发生拉断破坏（图14(d)），导致隧道管片封顶块发生脱落.

图14 内爆炸作用下地铁隧道管片及连接螺栓破坏特征[26]Fig.14 Failure characteristics of segments and connecting bolts in subway tunnel under internal explosion[26]

3 地铁隧道恐怖爆炸防护对策

城市地铁隧道一旦遭遇恐怖爆炸袭击，极易造成大量人员伤亡与经济损失，且会伴随恶劣的社会影响.因此，有必要针对地铁隧道恐怖爆炸袭击采取有效的防护对策，以避免或减轻地铁隧道恐怖爆炸袭击带来的损失和伤亡.

城市地铁隧道内恐怖爆炸的防护主要包含两个层面的涵义：一是采用措施降低地铁隧道内恐怖爆炸事故的发生概率，其目的是防止事故的发生；二是采取措施降低地铁隧道内恐怖爆炸事故的危害，其目的是降低已发爆炸事故的危害水平.下面从上述两层面简要论述地铁隧道恐怖爆炸防护对策.

3.1 降低恐怖爆炸事故发生概率的对策

防范恐怖主义和恐怖活动是每个公民的责任与义务.针对如何降低城市地铁隧道内恐怖爆炸袭击发生概率的课题，目前的主要对策包括以下几个方面：

① 面向社会定期开展反恐怖系列宣传教育活动，在广大人民群众中逐步形成自觉识别并抵制恐怖主义思想、积极配合有关部门反恐工作、踊跃举报涉恐可疑线索的社会风气；

② 严格执行爆炸危险品的安全监督管理制度，密切监控氯酸钾、硝化甘油、硝酸盐类物质等民用炸药原材料的市场流通；

③ 切实执行严密的地铁入口安检举措，保证充足的安检力量，不断提高安检人员及地铁运行管理人员的反恐素养及其对可疑人员的辨识能力；

④在地铁车站和隧道内关键部位配备用于探测爆炸物（器材）、阻爆、排爆的先进反恐装备和仪器，并持续改进已有技术与设备、研发新技术、新设备.

3.2 降低恐怖爆炸事故危害的对策

地铁隧道内发生恐怖爆炸事故所造成的危害主要体现在人员伤亡、隧道结构毁伤两个方面.因此，如何降低恐怖爆炸事故危害可从上述两个方面进行考虑.

恐怖爆炸袭击造成的人员伤亡事故等级与地铁管理服务人员应对事故能力、地铁乘客应急技能、应急救援力量等因素有关.为减轻人员伤亡，地铁管理服务人员应具备突出的应急疏通能力，其能力保障措施主要包括：①进一步提高应急疏通能力指标在地铁管理服务人员选拔、考核过程中的重要地位；②地铁管理服务人员应适时进行应急响应训练；③针对爆炸事故，地铁管理服务人员可积极开展应急教育宣传（例如，在出入口张贴宣传告示）.地铁乘客应积极参与演练，掌握必要的应急技能，这对于保障自身安全、减轻人员伤亡具有重要意义.此外，由公安、消防、医护以及社会救援力量组成的应急救援体系的迅速响应对于阻断爆炸事故的恶化、减轻受伤人员二次伤害具有重要作用.

恐怖爆炸冲击波荷载作用下隧道结构的毁伤效应直接受其抗爆能力控制.若地铁隧道结构抗爆能力不足，则无法承受恐怖爆炸冲击波效应，轻则造成结构碎片飞散伤人，重则造成隧道顶部坍塌，带来巨量经济损失与人员伤亡.提高地铁隧道结构抗爆能力的首要措施就是进行抗爆设计与抗爆加固设计.目前，我国新建地铁隧道的抗爆设计与实践以及已建地铁隧道的抗爆加固设计与实践仍处于初步发展探索阶段.

地铁隧道结构抗爆设计及抗爆加固设计可借鉴已经发展较为成熟的地上钢筋混凝土结构（建筑物）抗爆加固设计方法及研究成果，在结构材料、结构延性、结构受力特性、结构形式等的确定及选择方面应综合考虑抗爆性能与经济性的平衡.目前，地铁隧道结构抗爆防护的措施和方法主要包括：

① 在地铁隧道结构内壁贴装聚苯乙烯土工泡沫、发泡水泥基材料、泡沫铝、聚氨醋泡沫材料、玻璃钢蜂窝复合材料等具有良好抗爆吸能特性的新材料保护层，其防护原理为采用吸能材料吸收爆炸释放的能量，从而削弱爆炸冲击作用；

② 在地铁隧道结构内壁安装复合钢板，其防护原理为利用复合钢板出色的拉伸变形性能吸收爆炸释放的能量，从而提高隧道结构抗爆性能；

③ 采用配套用胶将凯夫拉（Kevlar）、玻璃纤维、碳纤维等高强度织物粘贴于地铁隧道结构表面，其防护原理为在不增加构件自重及体积的情况下有效封闭混凝土裂缝，并利用其优异的抗疲劳及减振性能提高隧道结构抗爆性能；

④采用特制的建筑结构胶将钢板粘贴于地铁隧道结构表面，其防护原理为在不增大构件截面尺寸的情况下提高构件承载力、刚度及延性；

⑤上述不同方法的组合使用.

4 未来发展及研究展望

基于已有技术研究文献以及笔者所在团队对该课题的长期研究与深入思考，笔者认为，恐怖爆炸冲击波荷载下地铁盾构隧道结构毁伤效应及防护对策的未来发展及研究工作中，以下几个方面的内容值得重视：

①地铁盾构隧道结构动力响应的研究手段需要进一步丰富和提升.目前，研究者们主要是采用数值模拟的手段开展研究，然而基于现场足尺试验、室内模型试验以及理论分析的研究还非常少见，因此应加强这方面的研究.特别地，室内模型试验（包括超重力离心模型试验和常重力缩尺模型试验）因其能够在相对安全和节约成本的条件下反映出地铁隧道结构的动力响应机理，具有较好的应用前景，但目前在相似比理论、相似材料选取、爆炸荷载模拟方法、管片接头的模拟等方面还需要进一步的研究与完善.此外，将数值模拟与机器学习相结合也是一个值得探索的有效研究手段.

②深入研究管片接头、地层特性、土与结构相互作用、管片间接触、地表超载、隧道埋深、隧道直径、管片厚度、爆源位置等重要参数对地铁盾构隧道爆炸响应的影响效应.

③考虑到爆炸恐怖袭击在时间和空间上的突发性和不可预知性，应加强多爆源同步和不同步起爆工况下的爆炸响应研究.多爆源工况的组合形式可以为：隧道内部不同位置组合；隧道内部、地层中不同位置组合；隧道内部、地层中、地表不同位置组合；地层中不同位置组合；地表不同位置组合；地表、地层中不同位置组合；地表、隧道内部不同位置组合.

④应进一步加强对爆炸冲击波荷载下地铁隧道结构塑性应变分布、结构损伤、裂缝分布、扩展及其演化规律的研究，并基于此开展长期稳定性、防渗性能、承受二次动荷载能力的评估与加固方面的研究.

⑤建议基于大量的数值分析和机器学习等手段的研究成果，提出能够考虑多种主要参数影响效应的简明实用经验公式，从而为爆炸冲击波荷载下地铁盾构隧道结构的抗爆设计结构优化及防护措施优化提供参考.

⑥目前的相关设计规范还暂未考虑可能发生的爆炸恐怖袭击对地铁盾构隧道结构安全与稳定的影响.但近年来发生在国外的地铁隧道爆炸恐怖袭击事件表明，结构安全是减少爆炸伤亡及经济损失的最基本的条件.因此，今后应加强该方面的概念、战略及理论设计，从而逐步将地铁隧道结构的抗爆设计与防护纳入到强制性规范中.

⑦进一步研发新型的爆炸物探测器材与技术，不断提高爆炸物探测技术的识别成功率及效率，并同时降低其使用成本.此外，排爆、阻爆技术还需进一步发展完善.

⑧进一步研发兼具抗爆吸能能力强、施工方便、经济环保等优势的地铁隧道结构爆炸防护新材料，并推广新材料在实际工程中的应用.

5 结 语

爆炸恐怖袭击是全人类的公敌，近年来在全世界范围内具有愈演愈烈的趋势.城市地铁隧道是重要的交通设施，在人们的日常生活中以及经济社会的发展中发挥着不可替代的作用，其目前的建设特别是在发展中国家的大中城市中的建设方兴未艾.城市地铁隧道由于其空间封闭性、人员密集、救援困难、抵御内部灾害能力弱等特点，更易成为极端分子开展爆炸恐怖袭击的对象，且一旦遭遇爆炸恐怖袭击，极有可能发生巨大的人员伤亡和经济财产损失.因此，地铁隧道的防爆问题逐渐引起世界各国研究者的重视，并取得了一定的研究成果.由于地铁隧道防爆的最基本的问题就是结构安全与稳定，因此爆炸冲击波荷载下地铁隧道结构的毁伤效应及防护对策成为了重要的研究课题.但由于研究手段的限制以及涉及的多场耦合现象及影响因素的复杂性，目前关于该方面的研究较少，且成果比较零散.

基于已有技术研究文献和本课题组的初步研究成果，作者团队对爆炸冲击波荷载下地铁盾构隧道结构的毁伤效应及防护对策研究进展进行了一定程度的归纳、总结与评述，并建议了几点值得重视的未来发展及研究方向，以期为我国恐怖袭击下城市地铁隧道爆炸毁伤效应研究与防护对策提供有益参考.