考虑斜坡约束的固定时间行星软着陆制导律设计

龚有敏，郭延宁，孙 悦，马广富，郭敏文，张海博

(1. 哈尔滨工业大学航天学院控制科学与工程系，哈尔滨 150001；2. 北京控制工程研究所，北京 100094)

0 引 言

随着航天技术的不断发展,各国也纷纷开展了深空探测任务,比如中国的天问一号火星探测器和美国的“毅力”火星探测器。随着深空探测任务的不断深入,火星采样返回和载人火星探测等任务也得到了广泛的关注。在未来开展采样返回等任务时,将探测器着陆到峡谷等危险地形更有利于采集到与水资源或者行星地质相关的样本。这就要求探测器能够具备在这些危险地形下安全着陆的能力。因此,研究能够实现精确软着陆并自主规避着陆过程的障碍的技术是极其重要的。在这些技术中,探测器的制导系统在保障探测器的安全着陆起到关键的作用,得到了广泛的研究[1-2]。

由于在阿波罗登月计划中的成功应用,阿波罗多项式制导[3]在过去的几十年内受到了学术界与工程界的广泛关注。阿波罗多项式制导的结构简单,易于在星载计算机上实现。为了满足更高的着陆性能要求,Lu[4-5]提出了增广的阿波罗式多项式制导和分数多项式制导,文献[5]中提出的分数多项式制导方法通过改变分数幂次和参数来改变着陆轨迹的曲率,具有规避障碍的潜能。

除此之外,现有的着陆制导方法可以分为计算最优制导[6-7]和反馈制导[8-10]两类。计算最优制导也叫作轨迹优化,这类方法是以燃料最优为出发点,通过求解最优化问题来得到控制加速度的数值解。这类方法中最具有代表性的是在文献[11]中提出的凸优化方法。近年来也有不少新的优化方法应用到着陆制导中,比如终端时间自由的凸优化方法[12]、协同优化方法[13]、多阶段凸优化方法[14]以及序列凸优化方法[15]。随着人工智能方法的发展,基于学习的优化方法也被用于求解最优着陆制导[16-17]问题。然而,计算优化制导方法得不到控制加速度的解析解,属于开环制导方法,鲁棒性差,依赖模型的准确度,而且需要进行大量的计算,增加了星载计算机的运算压力。为了提高系统的鲁棒性,获得解析的制导律形式,许多学者研究了反馈着陆制导方法。最有名的反馈制导方法是零控脱靶量/零控速度(zero-effort-miss/zero-effort-velocity,ZEM/ZEV)最优反馈制导[18-19],它是通过最小化整个系统能量来产生闭环的控制加速度指令。为了实现避障,Cui等[20]通过增加常值加速度段得到了可构建非凹着陆轨迹的ZEM/ZEV制导方法,该方法通过求解常值加速度的时间来实现避障。虽然该制导方法也适用于三维空间的着陆问题,但是该方法的推导仅针对二维平面,尚缺乏三维空间着陆问题的理论推导来严谨证明该制导方法在三维空间的有效性。Wang等[21]通过引入虚拟终端速度提出了两段ZEM/ZEV制导方法来实现避障。但是该方法需要通过求解优化问题来得到切换时间和虚拟终端速度。Zhang等[22]和Zhou等[23]等通过在性能指标中引入避障项对ZEM/ZEV制导律进行改进,避免了探测器与行星表面的碰撞,但这两个方法均未考虑行星表面凸起的障碍。除此之外,Gong等[24]通过构建阶梯形地形约束提出了基于预设性能的自主避障着陆制导方法,该方法需要提前获知障碍的精确信息。文献[25-27]采用势函数的方法设计了自主避障反馈着陆制导律,这些基于势函数得到的制导方法存在局部极小值的问题。

本文将着陆过程的自主避障作为主要研究问题。由于采用斜坡约束来实现避障具有不需要提前获知障碍的精确信息的优点,斜坡约束在许多计算最优制导算法中被用来约束轨迹以实现避障,但是现有的反馈制导中很少考虑斜坡约束。鉴于此,本文采用斜坡约束对着陆轨迹进行约束,研究满足约束的反馈制导律,实现自主避障精确软着陆。与现有方法相比,主要的创新点如下:

1) 研究了考虑斜坡约束的反馈制导问题,不仅满足了斜坡约束,还得到解析的控制加速度形式。此外,采用斜坡约束来约束着陆轨迹以实现避障无需提前获知障碍的精确信息;

2) 利用斜坡约束构建了一个新颖的非线性滑模面,既保证系统状态位于滑模面时是固定时间稳定的,又保证系统状态不会违反斜坡约束;

3) 通过设计反馈制导律,保证了滑模面能够在固定时间内收敛到0,并保持在滑模面上。在滑模面的收敛过程中,系统状态同样不会违反斜坡约束。

1 动力学模型与问题描述

1.1 动力下降段动力学模型

在动力下降过程中,探测器距离行星表面的高度较小(对于火星着陆而言,这个高度往往小于5 km),因此,在动力下降段中,可以忽略行星自转的影响,且可认为重力加速度是不变的。选取参考坐标系为与期望着陆点固连的非旋转坐标系,oz轴垂直行星表面向上,ox轴和oy轴位于行星水平面,构成右手坐标系。动力下降段的动力学模型为

(1)

1.2 斜坡约束

为了避免探测器在着陆过程中与行星表面凸起的障碍发生碰撞,可以采用斜坡约束对着陆轨迹进行约束。如果能保证着陆轨迹位于斜坡约束内,即可实现避障。在着陆任务中,可以先让探测器着陆到在期望着陆点的上方,然后再进行垂直着陆,例如火星科学实验室。因此,本文也是研究探测器着陆到期望着陆点的上方的虚拟着陆点,并采用如图1所示的斜坡约束对着陆轨迹进行约束,θ是斜坡角,zu是沿oz轴方向的单位矢量,h1为虚拟的着陆点高度,即虚拟着陆点的高度。

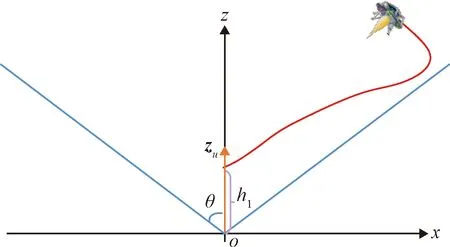
图1 斜坡约束Fig.1 Glide-slope constraint

根据图1可得斜坡约束的数学描述如下:

(2)

1.3 问题描述

在未来的行星探测任务中,为了获得更丰富的科学数据,可能会要求探测器能够精确着陆到较为复杂的地形,比如峡谷。为了保证探测器的安全,实现自主避障的精确软着陆成为需要解决的关键问题之一。因此,本文研究采用斜坡约束来约束着陆轨迹的行星探测器动力下降段精确软着陆反馈制导问题以实现自主避障。

2 考虑斜坡约束的反馈制导律设计

为了便于后续制导律的设计,本节首先给出本文用到的数学定义及基本引理。然后,再进行制导律设计与分析。

2.1 定义与引理

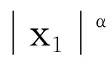
引理 1[28].考虑如下非线性系统

(3)

式中:f:U→Rn是连续函数。如果存在Lyapunov函数V(x)满足

(4)

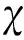
(5)

2.2 反馈制导律设计

为了避免探测器违反斜坡约束,根据式(2)定义的斜坡约束,设计着陆轨迹的约束边界函数为

(6)

求式(6)对r的梯度,可得

(7)

(8)

设计非奇异滑模面如下

s=μarctan(λe2+α1sigκ1(e1)+

(9)

式中:κ1>1,α1=diag(α1x,α1y,α1z)>0,β1=diag(β1x,β1y,β1z)>0,μ>0,k1>0。为了避免奇异,sc(e1)=[sc(e11),sc(e12),sc(e12)]T设计如下:

(10)

式中:0<γ1=p1/q1<1,η>0。为了保证滑模面的光滑性和连续性,参数l1和l2应该满足:l1=(2-γ1)ηγ1-1和l2=(γ1-1)ηγ1-2。

对式(9)求导可得

(11)

式中:ζ1,ζ2=diag(ζ21,ζ22,ζ23)的定义如下:

ζ1=κ1diag(|e11|κ1-1, |e12|κ1-1, |e13|κ1-1)

(12)

(13)

定理1.考虑式(1)所示的动力下降段动力学模型,和式(2)的斜坡约束,如果将滑模面设计为式(9),并将制导律设计为

(14)

证.1) 首先证明系统状态能够达到滑模面s并且滑模面s收敛的过程系统状态不违背斜坡约束

当s≠0时,由滑模面的定义(9)可知

β1sc(e1))-s

(15)

即

β1sc(e1))||+||s||

(16)

经上分析,只要能够证明滑模面在收敛过程是有界的,即可说明在滑模面收敛的过程中探测器的系统状态不会违反斜坡约束。

选取Lyapunov函数如下

(17)

求导,可得

-sTα2sigκ2(s)-sTβ2sigγ2(s)≤

-λmin(α2)||s||1+κ2+λmin(β2)||s||1+γ2=

(18)

式中:λmin(·)表示最小特征值。根据引理1可知,s满足固定时间稳定,而且收敛过程是有界的,即s收敛过程中不会违反斜坡约束。

2) 证明系统状态在滑模面上的收敛性并且系统状态沿着滑模面收敛的过程不会违反斜坡约束

如果系统状态位于滑模面上,即s=0,此时由式(9)有

(19)

左乘(λe2+α1sigκ1(e1)+β1sc(e1))可得

-μ(λe2+α1sigκ1(e1)+β1sc(e1))T×

arctan(λe2+α1sigκ1(e1)+β1sc(e1))

(20)

整理可得

arctan(λe2+α1sigκ1(e1)+β1sc(e1))-

(21)

选取Lyapunov函数为

(22)

求导可得

arctan(λe2+α1sigκ1(e1)+β1sc(e1))-

(23)

① 若|e1i|≥η,式(23)可写为

(24)

根据引理1可知,e1是固定时间稳定的。

② 若|e1i|<η,式(23)可写为

(25)

根据式(25)可知,此时系统状态也是稳定的。

进一步分析系统状态不会违反约束。当s=0且e1≠0时,由于

(26)

根据式(14)可知

(27)

进一步可知1/f2<∞,因此探测器的状态不会违反斜坡约束。

当s=0且e1=0时,由滑模面的定义可知,探测器的速度e2=0,说明探测器沿着滑模面滑动收敛到期望着陆点时,速度为0,即实现了精确着陆。

综上所述,采用所设计的滑模面和反馈制导律能够保证探测器在固定时间内精确着陆至期望着陆点,并且整个着陆过程中探测器不会违反斜坡约束,最终实现了自主避障。

注2.本文所设计的制导律要求探测器的初始状态是位于斜坡约束内的。

3 仿真校验

本节以火星探测器的动力下降段为例,分别在3.1节和3.2节给出仿真实例来校验所提算法的有效性。

仿真实例中,按照文献[11]选取探测器的参数,探测器的初始质量设置为m(0)=1 905 kg,火星表面的重力加速度为g=[0, 0, -3.711 4]Tm/s2,地球水平面的重力加速度为ge=9.807 m/s2,比冲为Isp=225 s。斜坡角为θ=60°,虚拟的期望着陆点高度为h1=5 m。

仿真中,制导律参数如表1和表2所示。

表1 制导律参数(一)Table 1 Parameters of the guidance law (Part 1)

表2 制导律参数(二)Table 2 Parameters of the guidance law (Part 2)

3.1 有效性校验

为了校验所提算法的有效性与正确性,本小节将考虑斜坡约束的制导律与去掉滑模面(9)中斜坡约束项推导得到的未考虑斜坡约束的制导律进行对比。未考虑斜坡约束的滑模面为

s=μarctan(λe2+α1sigκ1(e1)+β1sc(e1))

(28)

对应的未考虑斜坡约束的制导律为

(-(α2sigκ2(s)+β2sigγ2(s)))-

(29)

仿真结果如图2～图12所示。

图2 rx随时间变化曲线Fig.2 Time evolution of rx

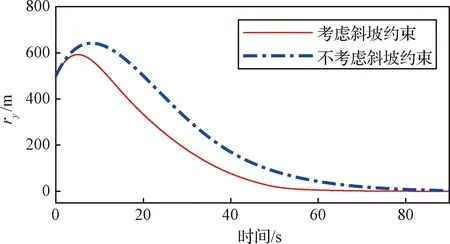
图3 ry随时间变化曲线Fig.3 Time evolution of ry

图4 rz随时间变化曲线Fig.4 Time evolution of rz

图5 vx随时间变化曲线Fig.5 Time evolution of vx

图6 vy随时间变化曲线Fig.6 Time evolution of vy

图7 vz随时间变化曲线Fig.7 Time evolution of vz

图8 ax随时间变化曲线Fig.8 Time evolution of ax

图9 ay随时间变化曲线Fig.9 Time evolution of ay

图10 az随时间变化曲线Fig.10 Time evolution of az

图11 三维空间着陆轨迹Fig.11 3D landing trajectory

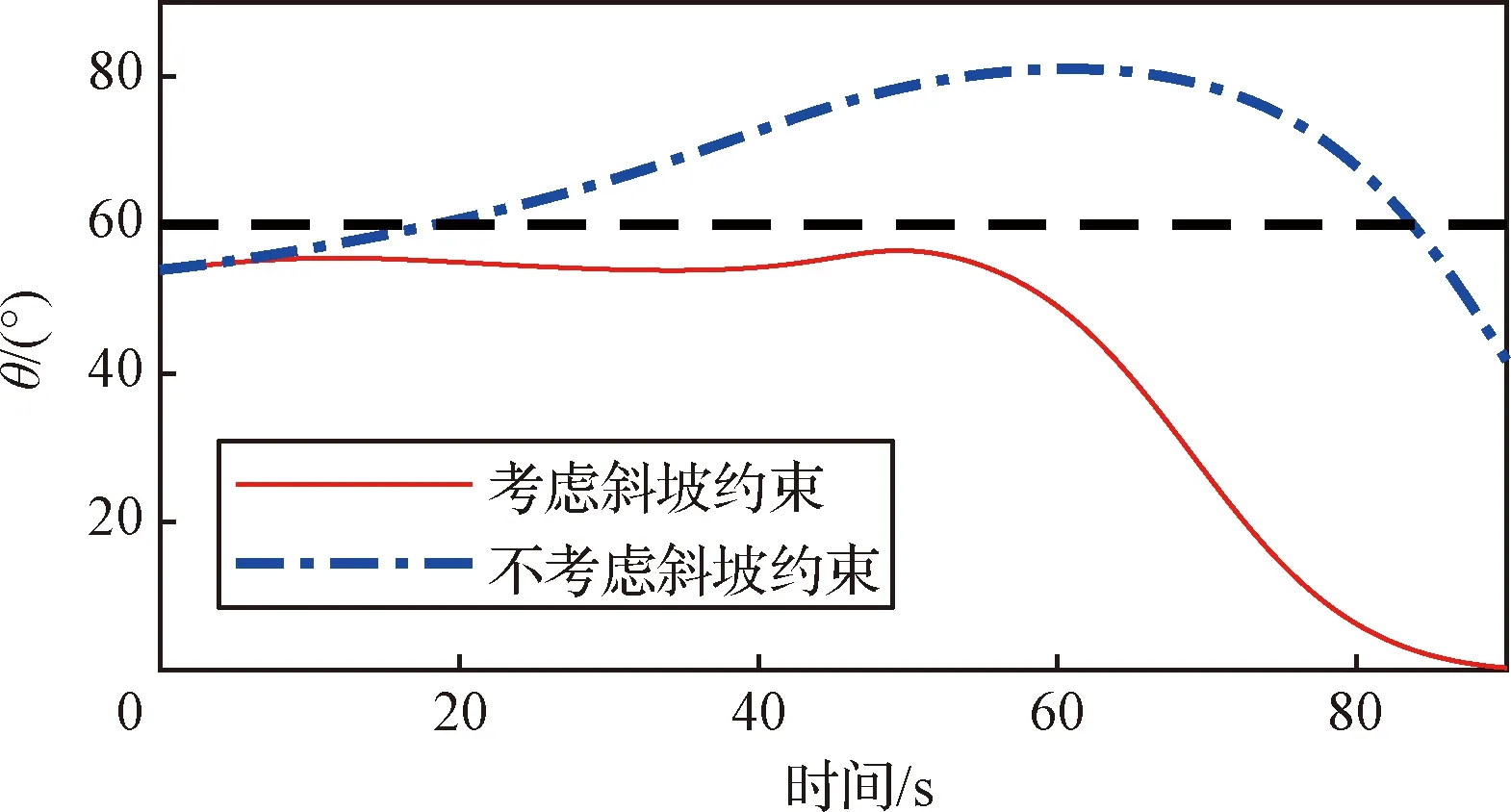
图12 斜坡角θ随时间变化曲线Fig.12 Time evolution of glide-slope angle θ

从图2～图7可以看出,采用所提的制导方法,探测器能够实现精确着陆。在斜坡约束项的作用下,考虑斜坡约束的制导算法使得探测器的横侧向运动以更快的速度向期望着陆点收敛,进而避免了探测器违反斜坡约束。

从控制加速度曲线图8～图10可以看出,考虑斜坡约束的制导律的控制加速度在大约45 s时开始增大,这是因为此时探测器距离斜坡约束较近,为了避免探测器违反斜坡约束,需要产生更大的控制加速度来控制探测器尽快远离斜坡约束。而未考虑斜坡约束的制导律的控制加速度在接近斜坡约束时没有施加额外的控制加速度来驱使探测器远离斜坡约束,进而违反了斜坡约束。从控制加速度曲线图8和图9可以看出,探测器横侧向运动的终端控制加速度为0,这意味着探测器在到达期望的虚拟着陆点时期望的俯仰角和横滚角为0。

从图11的三维着陆轨迹可以明显的看出,考虑斜坡约束的制导方法能够满足斜坡约束,实现自主避障,最终到达在期望的虚拟着陆点,而未考虑斜坡约束的制导方法会违反斜坡约束。同样,从图12所示的斜坡角θ的变化曲线也能明显看出,考虑斜坡约束的制导律能够的斜坡角始终满足斜坡约束的斜坡角,而未考虑斜坡约束的制导律在大约19 s时就已经违反了斜坡约束。

从仿真结果可以总结得到,在增加了斜坡约束项后,所提制导算法不仅能够保证探测器精确着陆到期望的着陆点,还能保证探测器在着陆的过程始终满足斜坡约束。

3.2 蒙特卡洛仿真

为了校验所提制导算法对初始状态偏差的鲁棒性,本小节进行500组蒙特卡洛仿真。探测器的初始状态如表3所示。仿真结果如图13～图16所示。

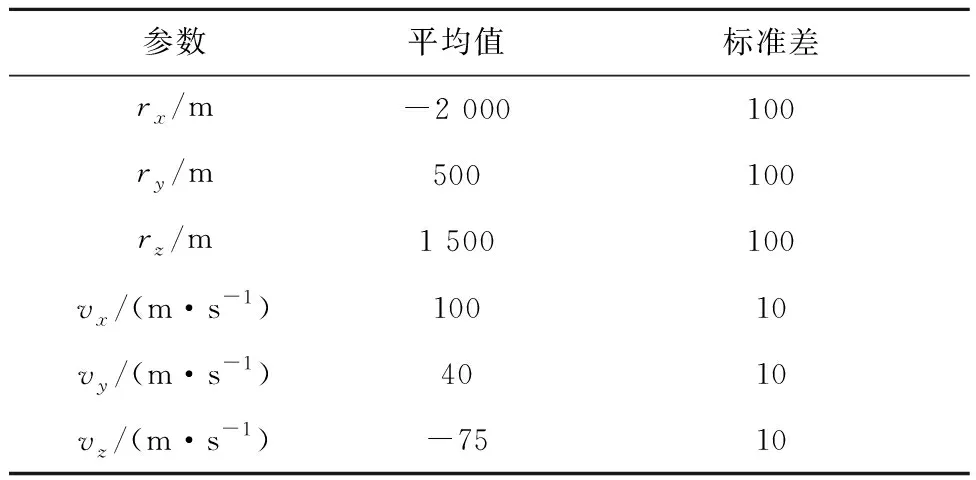
表3 蒙特卡洛仿真初值Table 3 Initial values of Monte Carlo simulations

图13 xoy平面的着陆误差Fig.13 Landing position errors on xoy plane

图14 着陆速度Fig.14 Landing velocities

图15 xoz平面着陆轨迹Fig.15 Landing trajectories on xoz plane

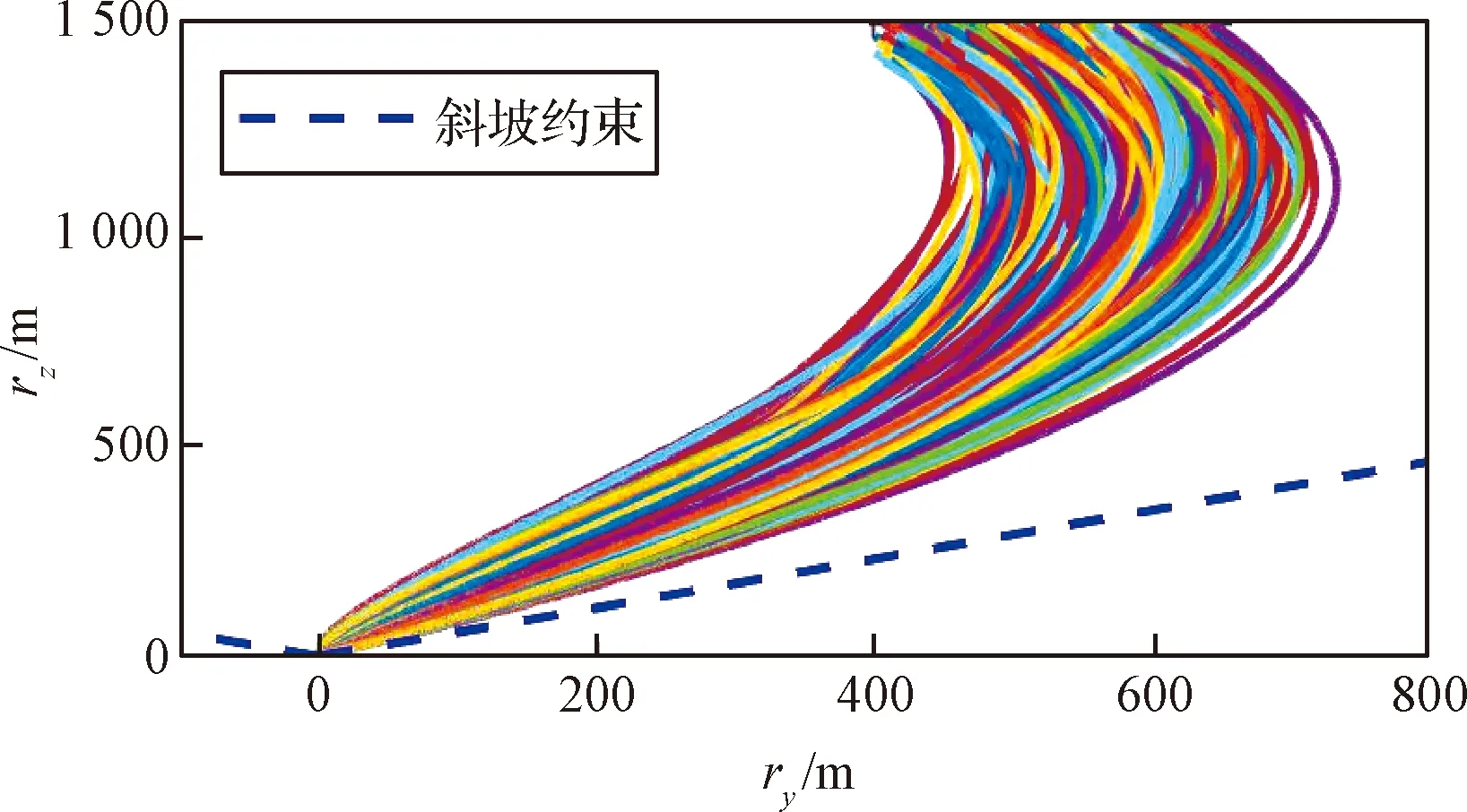
图16 yoz平面着陆轨迹Fig.16 Landing trajectories on yoz plane

根据图13和图14可以看出,在500组的蒙特卡洛仿真中,即使探测器的初始状态存在偏差,在所提出的制导算法作用下,探测器仍然能够以很小的速度精确着陆到期望的着陆点,且具有较高的着陆精度。

从图15和图16可以看出,在500组的蒙特卡洛仿真中,当存在初始状态偏差时,所提制导算法仍能保证探测器在着陆的过程不违反斜坡约束。从蒙特卡洛的仿真结果容易总结得到所提制导算法对初始状态偏差具有很强的鲁棒性。

4 结 论

本文研究了考虑斜坡约束的行星探测器动力下降段精确软着陆的固定时间滑模反馈制导律。通过在滑模面中引入斜坡约束,不仅能够保证系统状态沿着滑模面是固定时间稳定的,还能保证系统状态沿滑模面滑动收敛的过程不会违反斜坡约束。在上述滑模面的基础上,设计了精确软着陆反馈制导方法,保证滑模面的收敛过程是固定时间稳定的,而且在滑模面的收敛过程中探测器也不会违反斜坡约束。由于滑模面的趋近段和滑动段探测器均不会违反斜坡约束,保证了探测器始终满足斜坡约束,实现自主避障。通过数值仿真,校验了所提制导算法的有效性以及制导律对初值不确定性的鲁棒性。