非合作航天器相对运动估计的混合滤波器设计方法
2023-06-23张世源
卢 山,张世源
(1. 上海航天控制技术研究所,上海 201109;2. 上海市空间智能控制技术重点实验室,上海 201109)
0 引 言
近年来,中国航天领域的在轨服务任务日趋频繁,对于空间非合作目标,如故障或失效的飞行器、空间垃圾等的相对导航技术研究是当下的热点。对非合作目标的相对姿态、相对位置等信息进行精确的滤波估计,是实现在轨服务任务的基础,直接影响控制和制导的精度[1]。
为了体现追踪航天器与目标航天器间相对姿态与相对位置耦合的实时效应,提升相对状态估计的精度,文献[2-4]建立了非合作航天器相对运动的轨道-姿态的一体化滤波模型。这一类模型直接将量测设备获取的原始特征点的光学信息用于相对状态的估计,使状态变量维度过高(超过30维),在现有星上计算机的硬件能力下难以实现实时解算。本文考虑在非合作目标质心位置未知的情况下,将追踪航天器上量测设备输出的目标航天器形心的信息引入滤波方程,建立了追踪航天器与目标航天器相对运动的轨道-姿态的一体化滤波模型。相较以往研究中提出的模型,该模型的形式更加简洁且便于计算,并具有以下特点:状态方程由轨道相对运动模型与姿态相对运动模型构成,轨道相对运动模型为线性,姿态相对运动模型为非线性,且轨道与姿态相互解耦;观测方程为非线性,且与轨道相关的状态变量和与姿态相关的状态变量相互耦合。
利用上述模型进行非合作航天器相对状态量的估计属于非线性滤波问题。文献[5]提出了一种混合阶球面单形-径向容积卡尔曼滤波器(Mixed-degree spherical simplex-radial cubature Kalman filter,MSSRCKF)。MSSRCKF结合了三阶球面单形规则和五阶径向规则,使得算法能够以接近容积卡尔曼滤波器(Cubature Kalman filter,CKF)[6]的计算复杂度获得接近高阶CKF(High-degree CKF,HCKF)[7]的五阶精度,适用于高维度的强非线性系统。但由于本文建立的非合作航天器相对运动一体化滤波模型的状态方程中包含部分线性项,当使用非线性滤波器对模型全局进行处理时,部分计算成本将被浪费。文献[8-11]针对状态方程为非线性、观测方程为线性的情况,将非线性滤波器的时间更新公式与线性滤波器的量测更新公式相结合,使滤波器能够对模型中的线性与非线性模块分别采用相对应的滤波方式,提高了计算效率。文献[12]使用Rao-Blackwellized粒子滤波器对状态方程部分状态变量为线性、线性项与非线性项相互作用的系统模型进行估计,实现了非线性滤波算法采样点数量的降维。但上述研究均无法用于解决状态方程中线性项与非线性项相互解耦、观测方程中线性项与非线性项相互耦合这一更为复杂的情况。针对上述问题,本文通过在时间更新公式中加入线性项与非线性项之间互协方差矩阵的更新,将适用于线性系统的卡尔曼滤波器(Kalman filter,KF)[13]与MSSRCKF进行了融合,提出了线性-非线性混合卡尔曼滤波器(Linear-nonlinear hybrid Kalman filter,L-NLKF)。该滤波器能够对一个滤波方程中的线性与非线状态变量分别采用不同的滤波方式进行处理,在保证估计精度的同时,显著降低了计算量。
1 航天器相对运动的轨道-姿态一体化滤波模型
坐标系定义如下:
OI-XIYIZI:地心惯性坐标系FI。原点OI为地心,XI位于赤道平面内,指向春分点,ZI沿地球自转轴方向,向上为正,YI轴与XI轴和ZI轴构成右手直角坐标系。
OO-XOYOZO:第二轨道坐标系FO。原点OO位于航天器质心,ZO轴指向地心,XO轴在轨道平面内垂直于ZO轴指向航天器飞行方向,YO轴与XO轴和ZO轴构成右手直角坐标系。根据该定义可以分别得到追踪星第二轨道坐标系FCO与目标星第二轨道坐标系FTO。
OB-XBYBZB:本体坐标系FB。原点OB位于航天器质心,XB轴沿航天器主惯量轴指向前,ZB轴垂直于XB轴指向下,YB轴与XB轴和ZB轴构成右手直角坐标系。根据该定义可以分别得到追踪星本体坐标系FCB与目标星第二轨道坐标系FTB。
1.1 轨道相对运动模型
由于目标航天器为非合作,其轨道角速度未知,故将轨道相对运动模型投影在坐标系FCO中。假设追踪星在近距离捕获阶段轨道半径不发生较大改变,其轨道角速度n近似为常数。记坐标系FCB中两星质心的相对位置矢量为ρ=[x,y,z]T,线性化后的目标星质心相对追踪星质心的相对轨道动力学方程表示为
(1)
式中:wx,wy,wz为摄动力和模型误差引起的激励噪声。
由于非合作航天器的质心位置未知,而形心位置可以通过激光雷达数据建立的三维点云得到,故建立目标星形心坐标系FTF,其三轴指向与坐标系FTB一致。将两星的相对位置、相对速度以及目标星质心在坐标系FTF下的坐标(a,b,c)作为状态量,建立状态方程
(2)
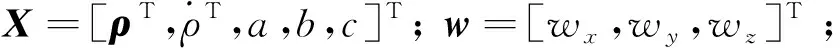
(3)
(4)
(5)
经离散化后的状态方程表示为
Xk+1=ΦXk+Γwk
(6)
式中:Φ∈R9×9为系统的状态转移矩阵;Γ∈R9×3为系统的干扰矩阵。
1.2 姿态相对运动模型
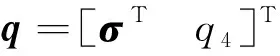
(7)
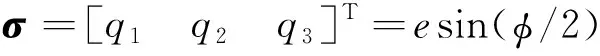
由单位四元数表示的相对姿态运动学方程为
(8)
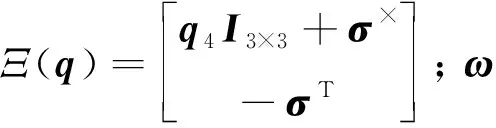
ω=ωIC-ωIT
(9)
式中:ωIC和ωIT分别为追踪星和目标星相对于坐标系FI的角速度。
坐标系FCB下追踪星相对目标星的姿态动力学方程为
(10)
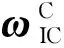
1.3 状态空间模型
1) 状态方程:
根据上述建立的相对运动模型,状态向量x定义为
(11)
得到具有加性噪声的连续非线性动态系统
(12)
式中:w为零均值高斯白噪声,协方差为Q;F(x)为关于状态向量x的非线性函数,可结合式(2)、(8)、(10)得到。
易知,此处轨道与姿态的相关状态量是解耦的。由于连续非线性动态系统不适用于计算机数值仿真,本文采用四阶龙格-库塔法[15]对其进行离散化处理。
2) 观测方程:
对于非合作目标的测量,星上量测设备输出的是坐标系FTF与单机测量系之间的相对位置与相对姿态信息。假设单机测量系与坐标系FCB重合,用rzx表示目标星质心在坐标系FTF中的坐标(a,b,c);rld为激光雷达的测量值,由追踪星质心指向目标星形心;rCT为两星质心连线(追踪星指向目标星)。上述矢量存在几何关系如下
(13)
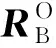
建立观测方程
(14)
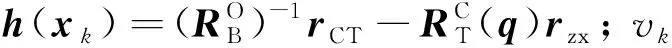
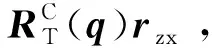
2 混合阶球面单形-径向卡尔曼滤波器
考虑如下的离散非线性动态系统
(15)
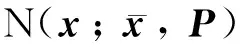
为了提高滤波精度以及降低计算复杂度,文献[5]将3阶球面单形积分准则与5阶径向积分准则相结合,提出了一种混合阶球面单形—径向容积卡尔曼滤波器(MSSRCKF)。MSSRCKF具有优异的非线性滤波性能。在维度较高的非线性系统中,MSSRCKF滤波精度接近于具有五阶泰勒精度的HCKF,而计算时间仅与CKF相当,适用于非合作航天器相对运动的轨道-姿态一体化滤波模型。
MSSRCKF的求积节点设置为:
(16)
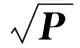
(17)
对应的权重系数为:
(18)
1) 时间更新
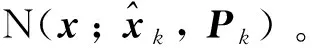
(19)
2) 量测更新
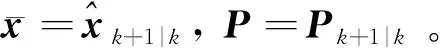
(20)
3 线性-非线性混合卡尔曼滤波器
式(12)为本文建立的非合作航天器相对运动模型的状态方程,其中F(x)由式(2)、(8)、(10)构成。式(2)为描述航天器轨道相对运动的线性方程,式(8)和(10)为描述航天器姿态相对运动的非线性方程,且式(2)与式(8)、(10)中的状态变量相互解耦。使用MSSRCKF进行滤波估计时,在式(19)所示的时间更新步骤中,该算法将对式(2)、(8)、(10)中包含的全部状态变量按式(16)所示的求积节点设置要求进行确定性采样。
确定性采样法是对服从高斯分布的状态变量经过非线性变化后的分布情况进行近似估计的方法[16]。由于式(2)为线性,服从高斯分布的状态变量通过该方程后的分布仍服从高斯分布,其均值和方差可直接由线性卡尔曼滤波公式求得。使用MSSRCKF的确定性采样法对式(2)进行处理时,并不会提高对应状态变量的估计精度,反而会对计算成本造成浪费。
针对上述问题,本文将应用于线性系统的KF与MSSRCKF进行了融合,提出了线性-非线性混合卡尔曼滤波器(Linear-Nonlinear Hybrid Kalman Filter,L-NLKF)。
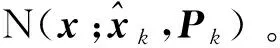
(21)
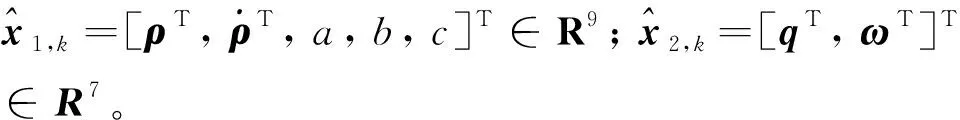
过程噪声wk也相应划分为w1,k∈R9与w2,k∈R7,对应的协方差矩阵分别为Q1,k∈R9×9与Q2,k∈R7×7。根据状态变量的划分情况以及协方差矩阵的性质,对协方差矩阵Pk进行分块
(22)
式中:P1,k∈R9×9为x1,k的协方差矩阵;P2,k∈R7×7为x2,k的协方差矩阵;P12,k∈R9×7为x1,k与x2,k的互协方差矩阵。
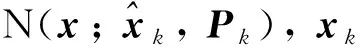
(23)
式中:f(·)由式(5)和(7)得到。
由于L-NLKF主要针对轨道-姿态一体化滤波模型中状态方程的特殊非线性形式进行设计,只需对MSSRCKF算法的时间更新方式进行改进,故本节仅给出L-NLKF算法时间更新的计算步骤:
1) 利用KF进行线性状态预测
(24)
2) 利用MSSRCKF进行非线性状态预测
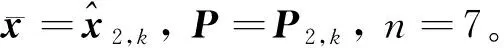
(25)
3) 利用卡尔曼滤波器进行x1,k协方差矩阵更新
P1,k+1|k=ΦP1,kΦT+Q1,k
(26)
4) 利用MSSRCKF进行x2,k协方差矩阵更新
(27)
5)x1,k与x2,k的互协方差矩阵的更新
互协方差矩阵P12,k的更新是L-NLKF算法的关键,本文将给出较为详细的推导过程。

P12,k|k+1=E[(x1,k+1|k-Ex1,k+1|k)(x2,k+1|k-
(28)
(29)
(30)
(31)
(32)
通过这种方式便可将高斯分布的加权二重积分问题转换为如式(30)所示的高斯分布的加权一重积分,并能够使用确定性采样的数值方法进行近似计算。式(30)中:ηi,k与ωi分别为求积节点与对应的权重。若对式(30)中的求积节点ηi,k重新进行求解,在增加了计算量的同时,由于一部分求积节点将被矩阵Θ1与Θ2归零,其中包含的分布信息将被浪费,且余下未被归零的求积节点不再能够完整的描述状态量的分布情况,使得滤波精度下降。
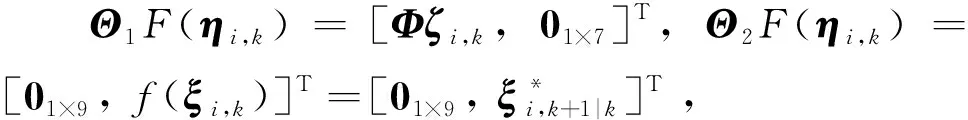
(33)
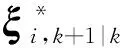
对x1,k进行确定性采样时,求积节点ζi,k应满足条件如下:
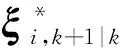
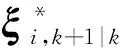
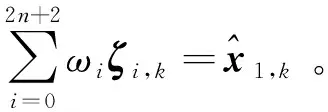
(34)
④ζi,k应满足协方差等式
(35)
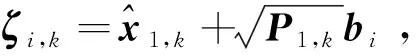
(36)
其中条件③、④为使ζi,k的前二阶矩与x1,k一致,以保证求积精度。根据上述条件,本文设置求积节点如式(37)所示。需要注意的是,满足上述条件的求积节点不唯一,本文选择其中的一种情况进行设置。当bi的解析表达式难以直接得到时,可以将bi中元素设为未知数,结合上述条件利用计算机求解多元非线性方程,得到bi的数值解。
(37)
6) 合并线性项与非线性项
(38)
(39)
4 仿真校验
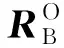

表1 航天器参数设置Table 1 Spacecraft parameter setting
滤波时长设置为120 s,步长为1 s;使用均方根误差(RMSE)来各滤波算法的精度。
(40)
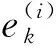
共进行NM=100次蒙特卡洛仿真,并将相对姿态四元数的计算结果转换为欧拉角,分别记为偏航角ψ、俯仰角θ、滚转角φ。滤波器估计误差对比如图1-图5所示。
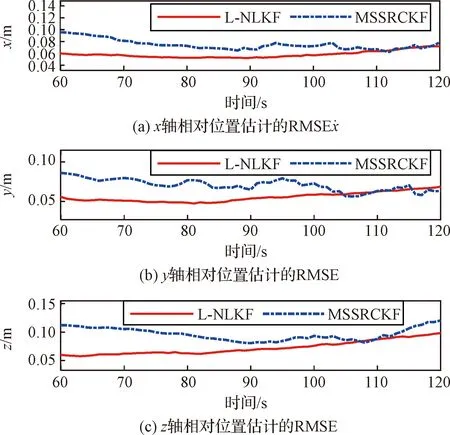
图1 相对位置估计的RMSEFig.1 RMSE of the relative position estimation
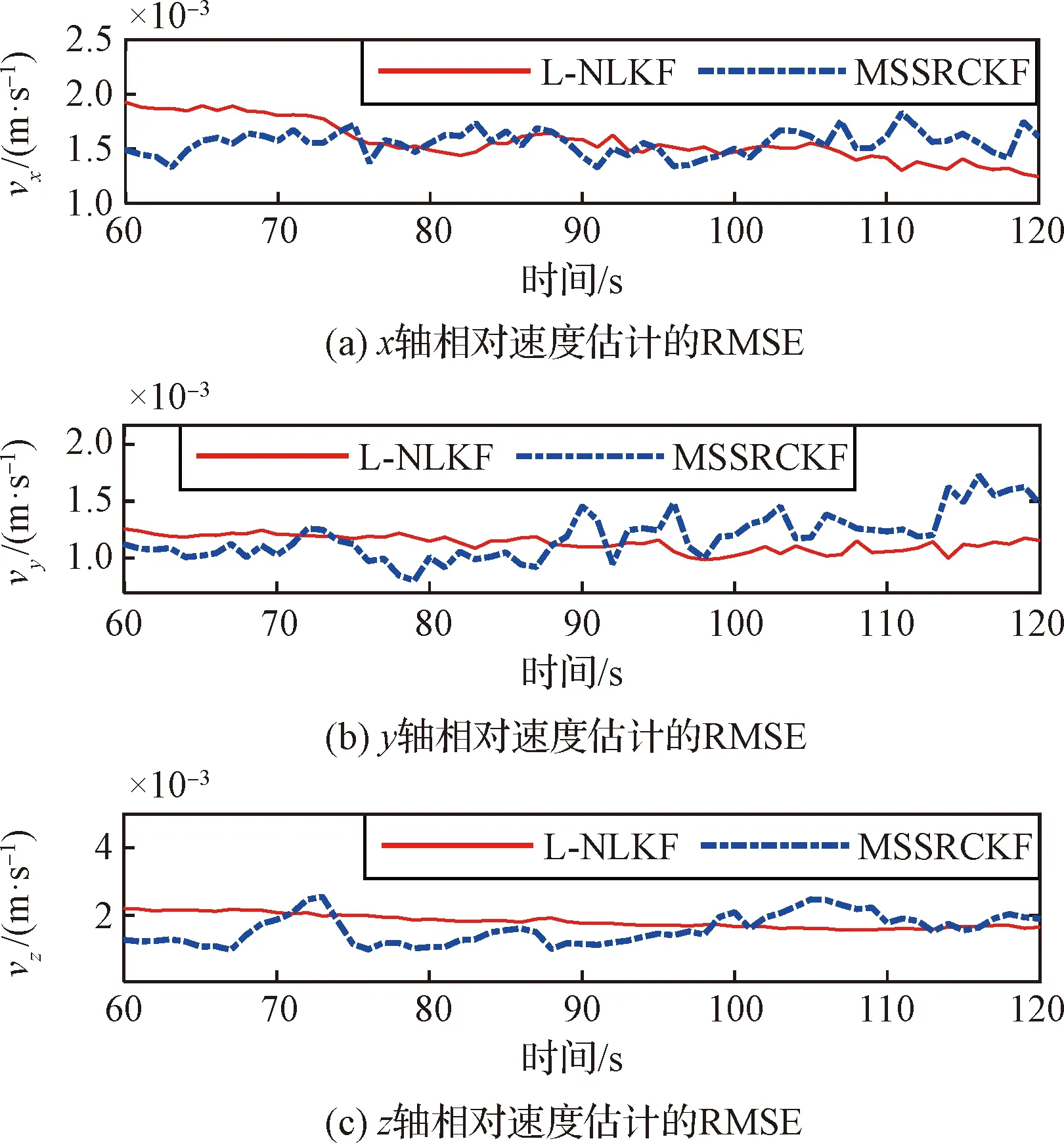
图2 相对速度估计的RMSEFig.2 RMSE of the relative velocity estimation
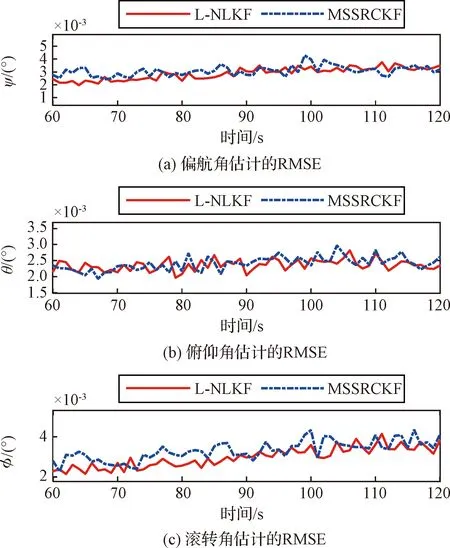
图4 相对姿态估计的RMSEFig.4 RMSE of the relative attitude estimation
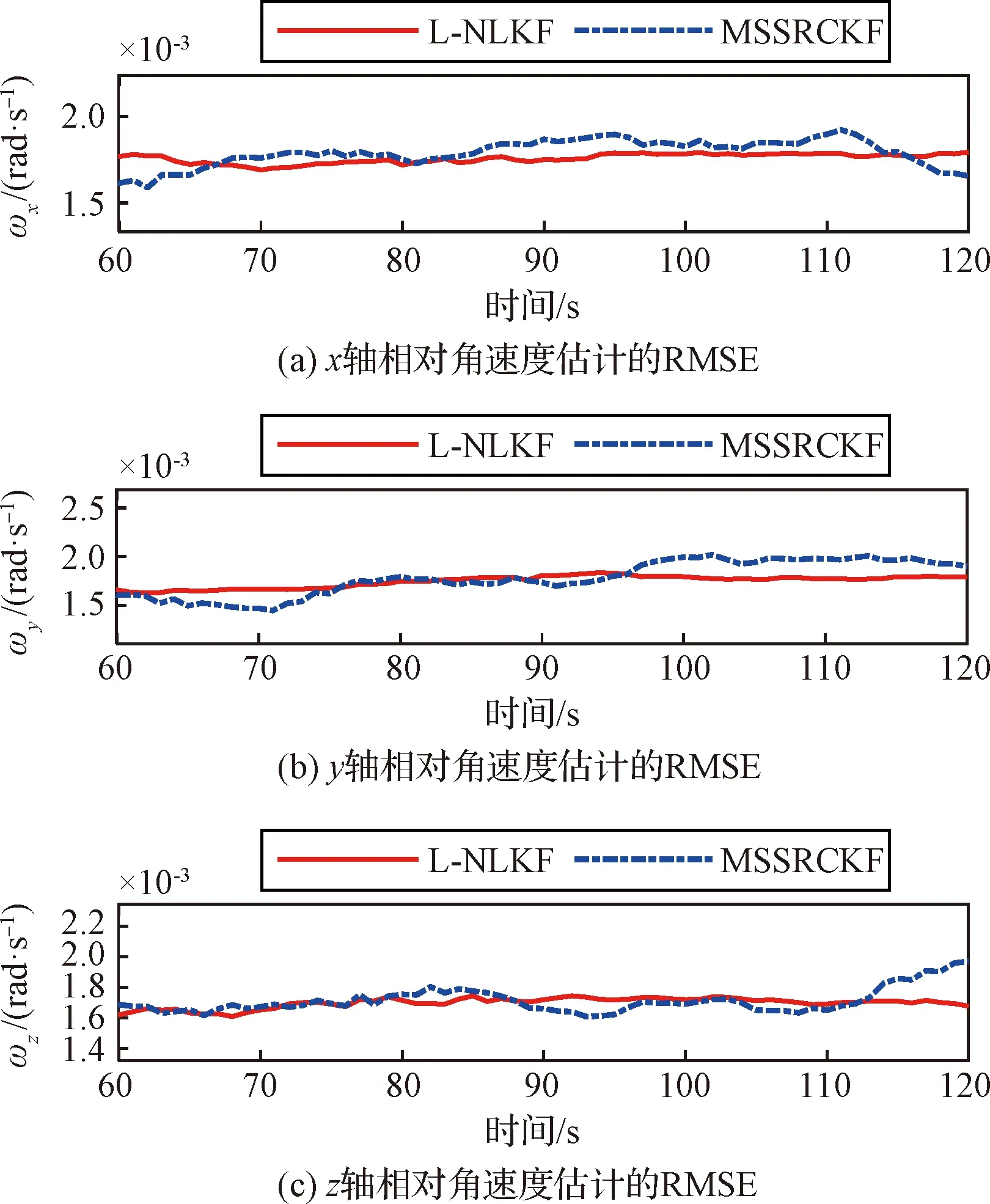
图5 相对角速度估计的RMSEFig.5 RMSE of the relative angular velocity estimation
由图可知,L-NLKF与MSSRCKF误差收敛后的RMSE基本一致。
为了定量描述滤波算法在总体上的精度,定义航天器相对位置、相对速度、目标质心位置与相对角速度的平均RMSE(Time-averaged RMSE,TARMSE),如式(41)所示
(41)
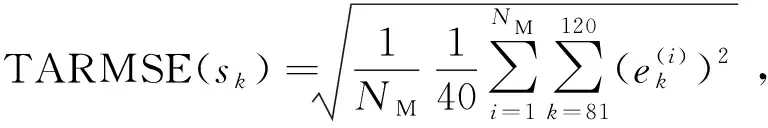
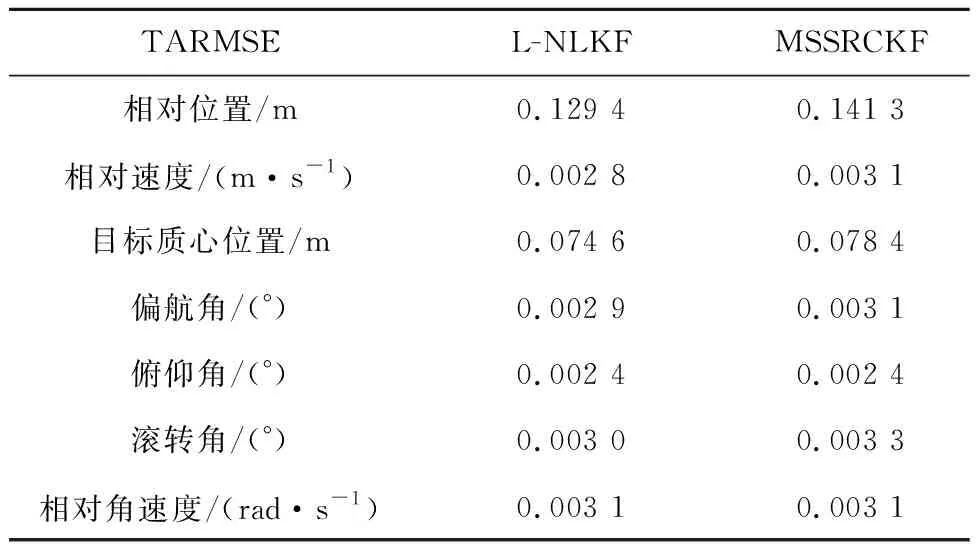
表2 滤波算法性能比较(情况1)Table 2 Performance comparison of filtering algorithms(case 1)
由于航天器间相对角速度的大小对滤波估计的影响较大,考虑目标快速旋转情况,将相对角速度初值扩大100倍,即ω0=[1.32,1.32,2.64]T×10-1rad/s,其余初值不变,再进行一组蒙特卡洛仿真。统计结果如表3所示。
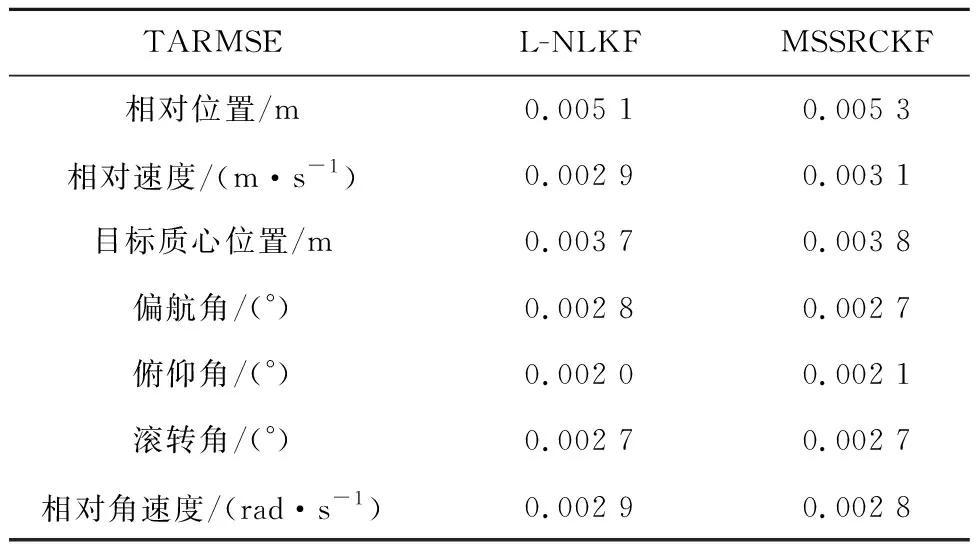
表3 滤波算法性能比较(情况2)Table 3 Performance comparison of filtering algorithms(case 2)
对比表2、表3可知,与航天器间相对角速度接近于零(无相对转动)相比,目标快速旋转时,相对位置与目标形心位置的估计精度显著提升。这是由于目标快速旋转时,目标形心与质心的偏差矢量也在追踪航天器的观测中发生明显变化,即更易对相关状态变量进行测量。
定义滤波器单步平均运算时间为
(42)
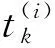
计算得到L-NLKF的单步平均运算时间为1.2 ms;MSSRCKF的单步平均运算时间为2.2 ms,即L-NLKF的单步计算时间仅是MSSRCKF的55%。结合表2、3中的数据可知,在非合作目标相对追踪航天器低速、高速旋转的两种情况下,L-NLKF均能在保证估计精度的基础上,大幅缩短计算时间。
5 结 论
本文提出了L-NLKF算法,进行了理论推导,提高了计算效率。主要工作包括以下几个方面:
1) 根据星上量测设备获取的目标形心的相对位置与相对姿态信息,建立了非合作航天器相对运动的轨道-姿态一体化模型。相较以往的研究,该模型维度较低、更加便于计算。
2) 针对非线性滤波过程中,状态方程包含部分线性项的问题,将KF与MSRRCKF进行了融合,提出了L-NLKF。该算法能够对状态方程中的线性项与非线性项分别用不同的滤波方法进行处理,同时利用分块的方式降低矩阵运算的维度显著提升了计算效率。
3) 航天器相对运动的仿真实验对比表明,本文提出的L-NLKF在保证了滤波精度的前提下,计算时间明显少于MSSRCKF。
