地面多目标快速响应任务轨道设计

张海洋，张 刚

(哈尔滨工业大学航天学院卫星技术研究所，哈尔滨 150001)

0 引 言

快速响应空间技术旨在对用户指定的目标点进行快速、及时的成像观测,以提高空间情报能力。比如,当某地发生地震、森林火灾等自然灾害时,响应卫星需要在较短的时间内,快速到达受灾点上方,为救灾工作提供地面图像信息支撑[1-2]。

为提升对应急任务的空间响应能力,可利用在轨航天器轨道机动,调整其星下点轨迹,实现对指定目标点的过顶访问,根据机动方式不同,可分为连续推力[3-5]和脉冲机动[6-9]两类。然而,由于应急任务的突发性和目标点位置的随机性,若给定的时间区间内,目标点超出在轨航天器机动能力的可达范围[10],则无法通过轨道机动实现访问任务。此时,需要快速组装、发射新的响应卫星,同时需要进行响应轨道设计。

一般空间轨道设计任务往往追求对整个地面空间的覆盖,以地面覆盖率、空间分辨率等作为优化指标[11-12]。此外,为保证重访或相同的光照条件等特性,常采用回归轨道[13-14]、太阳同步轨道[15]等。与一般的轨道设计任务相比,面向快速响应任务的轨道设计具有应急性、短暂性、局部性等特点,通常只要求在一段时间内对用户指定的地面目标点进行详细侦察。然而,受响应卫星自身狭窄视幅宽的限制(例如,法国Pleiades卫星,成像幅宽仅为20 km,对应赤道上经度范围0.18°),要求设计轨道的星下点轨迹能够精确经过目标点。此外,对于快速响应任务,若将目标点设置为发射场,则响应卫星在发射后无需轨道机动可直接进入设计轨道,从而对其它地面目标进行访问(如文献[16]提出的近地快速覆盖轨道),这可以大大减少应急任务的响应时间。

对于单个给定的地面目标点,Li等[17]提出了一种回归轨道设计方法,其星下点轨迹能够在升轨段和降轨段对目标点进行交替访问,从而缩短重访时间。对于两个地面目标,文献[18-19]分别提出了在入轨后单个轨道周期和多个轨道周期内访问目标点的回归轨道设计方法。上述研究均考虑了J2摄动的影响且设计的轨道都为圆轨道。然而,圆轨道在具有所有目标访问高度一致这一优点的同时,也由于设计变量少,限制了访问目标的个数。对于3个地面目标,Abdelkhalik[20]提出了二体模型下两种椭圆轨道的设计方法,并指出对于任意3个地面目标,存在多条访问轨道。然而,文献[20]中没有考虑回归约束,设计的轨道仅能访问目标点一次。

总之,目前在根据指定地面目标点设计航天器轨道的研究中,只有针对3个目标点单次访问,或两个及以下目标点多次重复访问的轨道设计方法。考虑到响应卫星的发射成本较高,若能够在单次发射任务中同时访问更多的目标,能够大大提升工作效率,降低任务成本。

本文提出了一种面向多目标快速响应任务的轨道设计方法。通过该方法设计轨道的星下点轨迹能够精确通过用户给定的地面目标,实现对4个地面目标点的多次重复访问,或对5个地面目标点的单次访问。本文考虑J2摄动的影响。

1 问题描述与分析

假设在初始时刻为t0的某次应急响应任务中,用户指定了n个地面目标,其位置信息以地心经、纬度的形式给出,记为(λk,φk),k=1,2,…,n。航天器在t时刻的轨道六根数用ξt=[a,e,i,Ωt,ωt,ft]表示,分别为半长轴、偏心率、倾角、升交点赤经、近地点角距和真近点角,ut=ωt+ft为参数纬度幅角。现需要求解初始时刻对应的ξt0,使航天器的星下点轨迹能够在tk时刻精确通过第k个地面目标,并在一定时间内实现对n个目标点的全部访问。

在本问题中,对于每个地面目标点的访问,均存在经度和纬度两个等式约束,因此,n个目标点共有2n个等式约束。假设航天器初始时刻在第1个目标点(如发射站)上方,则待求的未知量为初始时刻的轨道六根数ξt0=[a,e,i,Ωt0,ωt0,ft0]和对其余n-1个目标点的访问时刻tk,k=2,…,n,即n个目标点共有5+n个未知变量。

由上述分析可知,5个地面目标可确定响应卫星的轨道,未知数和等式约束个数均为10,存在离散的解。此外,若要求设计轨道为回归轨道(相应增加一个等式约束,详见第2节),则4个地面目标可确定响应卫星的轨道,未知数和等式约束个数均为9,同样存在离散的解。

虽然该问题易于定性分析,但无论对于5个地面目标单次访问问题中的10个未知数,或4个目标重复访问问题中的9个未知数,在求解过程中均面临着初始猜测难以选择的问题。因此,若能通过理论推导将初始问题进行降维简化处理,减少约束方程和未知量的个数,将大大减小问题的求解难度,这一过程将在后续进行具体推导和介绍。

2 目标访问约束

航天器在轨运动会受到各种摄动力的干扰,从而使轨道偏离二体运动,本文考虑地球扁率摄动即J2摄动的影响。J2摄动会导致轨道根数发生长期漂移和周期震荡,忽略其中周期项的影响,航天器轨道参数的漂移率可由线性J2模型[21]得到为

(1)

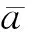
星下点是航天器位置矢量在地球表面的投影,可由轨道参数和格林尼治平衡星时角计算得到。航天器在tk时刻的星下点可表示为地心经、纬度(λ,φ)[21],即:

(2)

φ(tk)=arcsin(sinisinutk)

(3)

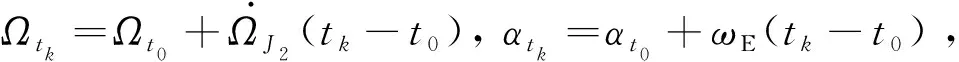
本文要求航天器的星下点轨迹能够精确通过指定的地面目标,因此,对于位置信息为(λk,φk)的第k个目标点,其访问约束可表述为

λ(tk)-λk=

(4)

φ(tk)-φk=arcsin(sinisinutk)-φk=0

(5)

注意,星下点轨迹是航天器在轨运动和地球自转运动的合成,当航天器运行至与目标点k同一纬度时,对应的参数纬度幅角utk可由式(5)求解得到为

(6)

式(6)中的两个值分别对应升轨段访问和降轨段访问。当参数纬度幅角确定后,对应的访问时刻tk与初始时刻t0之间的时间差可通过开普勒方程[21]计算得到为

(7)

式中:Nk为访问圈数;Mt0和Mtk分别为初始时刻和访问时刻的平近点角。在tk时刻航天器与目标点处于同一纬度φk(如图1所示),此时,仅需满足经度约束λ(tk)-λk=0。将式(7)代入式(4),整理可得:

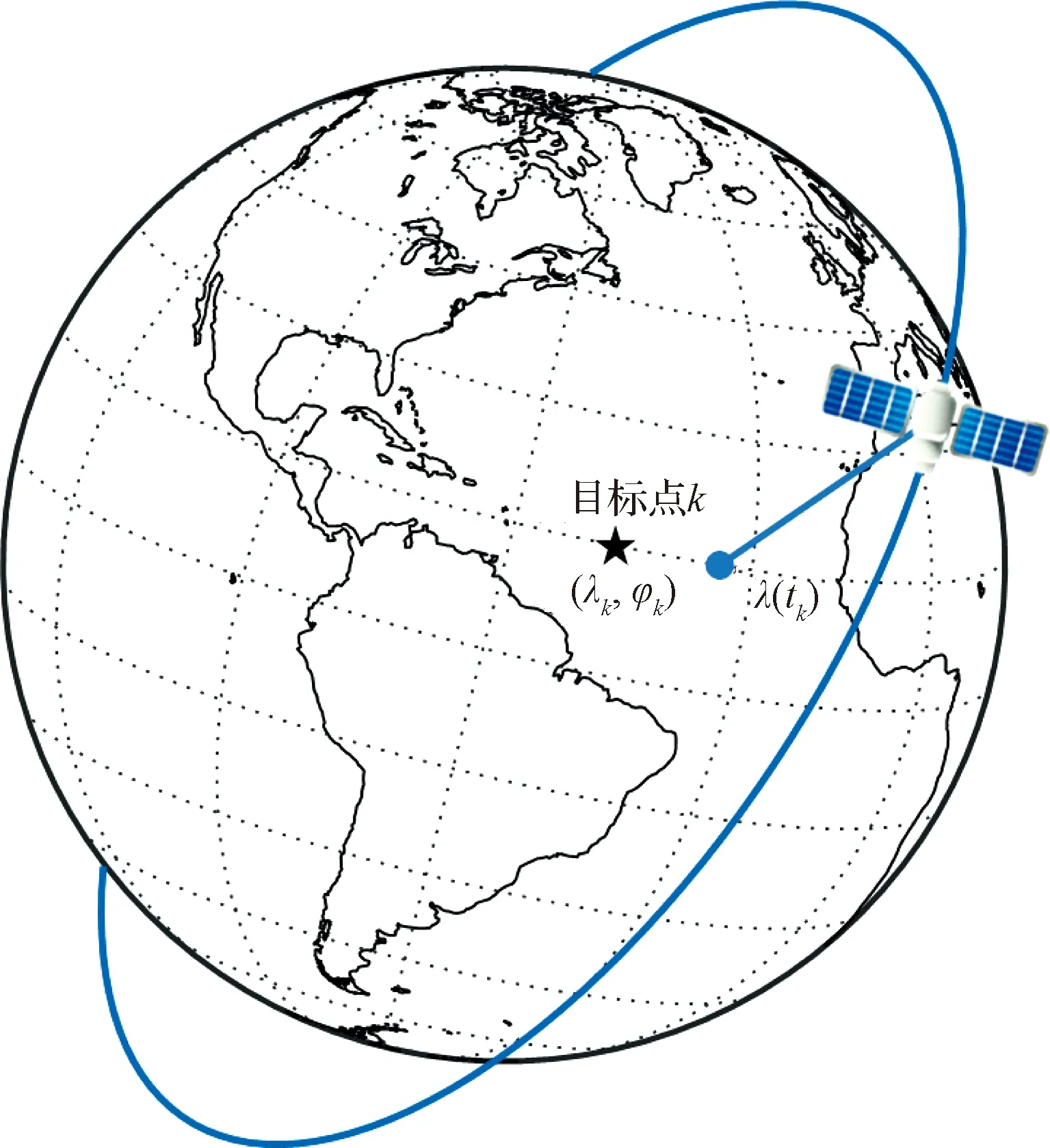
图1 航天器与目标点处于同一纬度Fig.1 A spacecraft at the same latitude as the target point

λ(tk)-λk=

(8)

值得注意的是,为保证初始时刻航天器在第一个目标点上方,初始时刻的参数纬度幅角ut0还需满足

(9)

综上所述,5个地面目标单次访问问题可表述为5个式(8)约束(式中k=1,2,3,4,5)和1个式(9)约束,未知量为初始时刻的轨道六根数。未知量和约束方程个数相等,存在离散的解,该结论与第1节一致,即5个目标可确定响应卫星的轨道。

若要求航天器能够实现对目标点的重复访问,设计轨道还需满足回归约束

NTnod=DTE

(10)

式中:N和D为互质的整数,表示航天器在经过D个恒星日运行N圈后星下点轨迹开始重复,从而实现对目标点的重访;Tnod为航天器的交点周期,TE为地球相对于轨道面旋转一圈的时间间隔,二者表达式为

(11)

在回归约束下,4个目标点重复访问问题可表述为4个式(8)约束、1个式(9)约束和1个式(10)约束,未知量为初始时刻的轨道六根数。未知数和约束方程个数相等,同样存在离散的解,结论与第1节一致,即在回归约束下4个目标即可确定响应卫星的轨道。

注意,为避免赘述,后续设计流程中的公式仅显示升轨访问,若有目标点选择在降轨段访问只需根据式(6)、(8)、(9)进行相应调整即可。

3 假设倾角已知下其余轨道元素设计流程

由第2节分析可知,5个目标单次访问问题和4个目标重复访问问题均可表示为六维非线性方程组的求解问题。为避免直接求解六维非线性方程组时初始猜测难以选择的问题,本节先假设轨道倾角已知,通过解析或数值方法依次对其他轨道参数进行求解。

3.1 参数纬度幅角和升交点赤经求解

假设轨道倾角i已知,由式(6)可知,轨道倾角需满足sini≥sinφk,即i∈[|φk|max,π-|φk|max]。由于初始时刻航天器在目标点1上方,有t1=t0,初始时刻的参数纬度幅角ut0可直接由式(9)解析得到。

将t1=t0代入目标点1的访问约束方程[式(8),k=1],可得到设计轨道的升交点赤经为

Ωt0=αt0+λ1-arctan(cositanut0)

(12)

下面对其余目标点的访问圈数进行估计。当倾角i和升交点赤经Ωt0均确定后,航天器的轨道平面即确定,当轨道面扫过目标点(λk,φk)时,有[22]:

(13)

令sinβg1, cosβg2,通过四象限反正切计算得到β,对应的格林尼治平恒星时角为αtk=Ωt0+β。由此,转移时间可由格林尼治平恒星时角之差与地球自转角速度估计得到[22],为

(14)

式中:d表示在第d天过顶访问。对第k个目标的访问圈数可由下式计算得到

(15)

3.2 偏心率和近地点角距求解

分别联立对第2、3个目标和对第3、4个目标的访问约束方程[式(8),k=2,3和k=3,4],消去设计轨道的平均角速度和J2摄动下轨道的漂移,可得到如下F1和F2两个非线性方程

(16)

(17)

式中:Ωt0,αt0和λk均为已知量;圈数Nk在式(15)估计的区间内遍历搜索得到;utk可通过式(6)计算得到;平近点角Mtk可通过对应的偏近点角计算得到为[21]

Mtk=Etk-esinEtk

(18)

偏近点角与真近点角之间的关系为[21]

(19)

而真近点角ftk=utk-ωtk≈utk-ωt0,此处忽略了J2摄动对近地点角距的影响[23]。当参数纬度幅角utk已知时,平近点角Mtk仅与偏心率e和近地点角距ωt0有关。因此,方程组F1和F2中仅含有未知量偏心率e和近地点角距ωt0,求解方程组的零点即对应设计轨道的e和ωt0。

二维非线性方程组可通过牛顿迭代求解,迭代公式为

(20)

(21)

令x表示ωt0或e,有

(22)

式中:

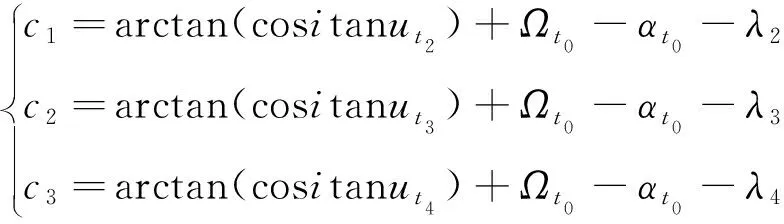
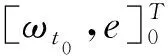
首先,通过对偏心率一阶泰勒展开,式(19)中偏近点角可近似为[8]

Etk≈ftk-esinftk

(23)

由此,式(18)中平近点角可近似为

Mtk≈ftk-2esinftk≈(utk-ωt0)-2esin(utk-ωt0)

(24)

然后将式(24)代入式(16),可将偏心率e表示为只关于近地点角距ωt0的函数,

(25)

式中:

将式(25)代入式(17),可得到只含有近地点角距ωt0的一维非线性方程,可通过数值方法(如二分法、割线法等)求解其零点得到ωt0的初值,代入式(25)即可得到偏心率e的初值。

将初始猜测代入式(20)求得ωt0和e的精确解后,初始时刻的真近点角为ft0=ut0-ωt0。

3.3 半长轴求解

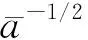
(26)

式中:

(27)

当仅存在4个目标点,而无其他约束条件时,可给定一个大于所有目标点纬度的倾角i,其余初始时刻的5个轨道要素可通过上述步骤依次求解,其中参数纬度幅角、升交点赤经分别通过式(9)、(12)解析得到;偏心率和近地点角距通过式(20)牛顿迭代数值求解得到;半长轴通过求解七次多项式,即式(26)数值得到。求得的轨道参数可实现对4个目标点的单次访问。

4 轨道倾角求解

本节将在上一节的基础上,对轨道倾角进行设计,以满足回归约束,或更多目标点的访问约束。

4.1 4个目标重复访问回归轨道设计

若仅给定4个目标点,则可在第3节的基础上,对倾角i进行设计,使设计的轨道满足式(10)的回归轨道约束,从而实现对目标点的重复访问。首先根据任务需求,人为选定回归天数D和圈数N,在此基础上,对于一个给定的倾角i,其他5个要素均可通过第3节计算得到。因此,式(10)可看作仅含有倾角i的一维非线性方程。在倾角的取值区间内,通过一维搜索求解其零点,得到回归约束下的倾角i,然后代入第3节,更新得到其余5个轨道要素。

注意,在第3.1节的访问圈数的计算中,当N和D给定后,轨道半长轴的初始猜测可由式(10)在二体模型下直接计算得到:

(28)

至此,t0时刻6个轨道要素全部求解完成,完成4个目标回归轨道设计。

4.2 5个目标单次访问轨道设计

若给定5个目标点,同样可先假设倾角i已知,其他5个要素均可通过第3节计算得到,实现对前4个目标点的访问。由此第5个目标点的访问约束

λ(t5)-λ5=arctan(cositanut5)+Ωt0-αt0-λ5+

(29)

也可看作仅含有倾角i的一维非线性方程。在倾角的取值区间内,通过一维搜索求解其零点,得到满足5个目标访问约束下的倾角i,然后代入第3节,更新得到其余5个轨道要素。

至此,t0时刻6个轨道要素全部求解完成,完成五个目标单次访问轨道设计。

4.3 整体设计流程

对于每个地面目标,均有升轨段访问和降轨段访问两种访问弧段,见式(6)、(8)、(9),具体可根据任务需求进行选择。当地面目标无特定访问弧段要求时,n个目标共有2n种访问弧段组合,对于给定的目标访问弧段组合,每个目标访问圈数的取值区间可由式(15)估计得到,遍历取值区间内所有圈数组合,即可得到当前访问弧段组合下的所有解,算法流程图如图2所示。

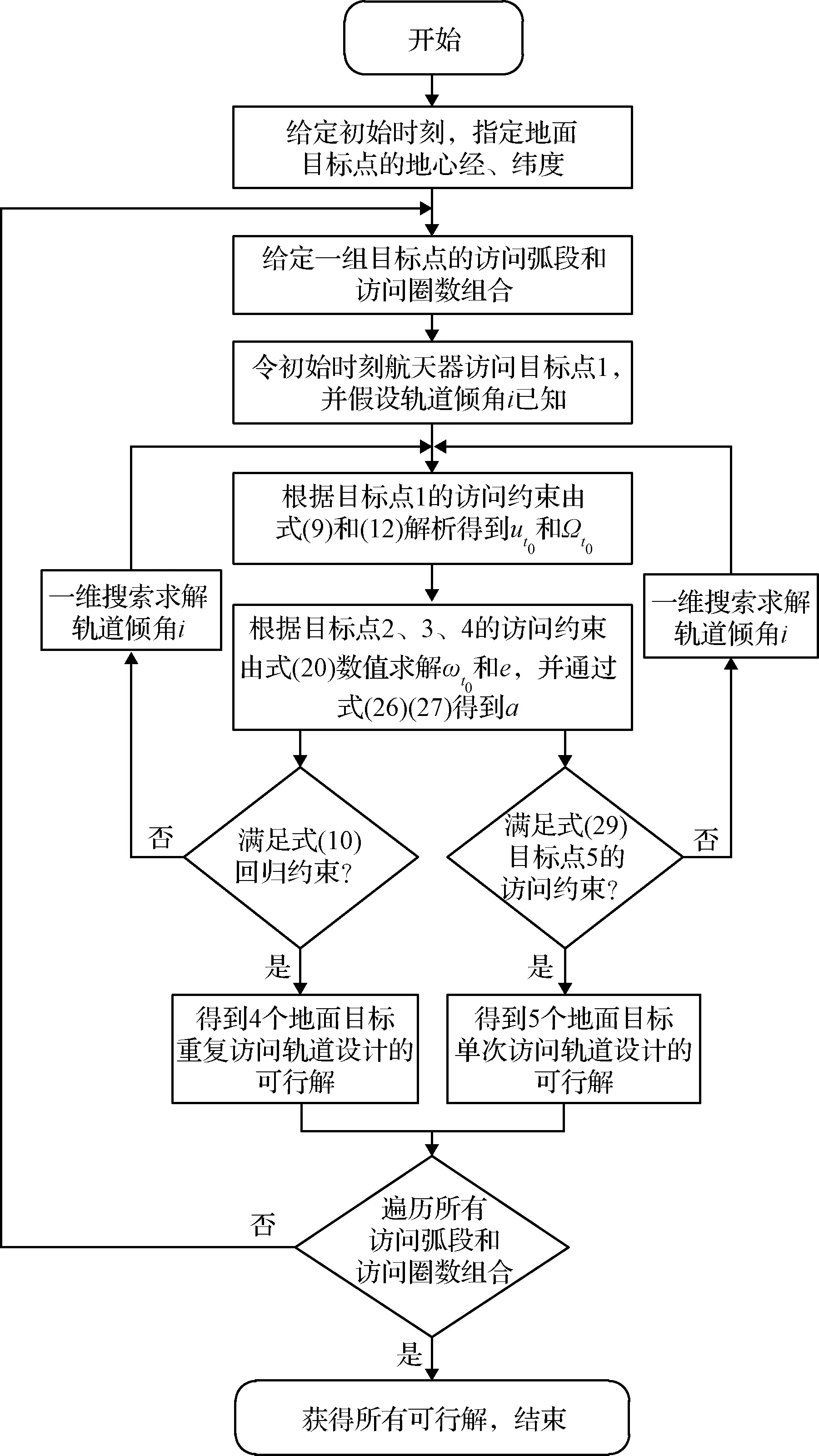
图2 轨道设计算法流程图Fig.2 Flow chart of the orbit design algorithm

对于每一组给定的访问弧段和访问圈数组合,4个目标重复访问问题和5个目标单次访问问题都被转化为关于倾角的一维非线性方程求根问题。一维非线性方程可通过一维搜索求解其零点。具体而言,首先将倾角在[|φk|max,π-|φk|max]内离散,通过网格法搜索得到倾角的可行区间(注意,在某些给定倾角处,其它轨道参数无解或不符合实际,如轨道高度过低撞地等,非线性方程无意义)。接下来,通过分段黄金分割搜索得到区间内所有的极值点,若两个相邻极值点处的函数值异号,则之间一定存在解,进一步通过割线法精确求解方程零点。

5 仿真校验

本节提供了几个算例来校验文章所提方法的有效性。初始时刻设置为2022年1月1日00∶00∶00,对应的格林尼治平恒星时角为αt0=1.756 3 rad,用户指定地面目标点的地心经、纬度如表1所示。现要求设计航天器的轨道,实现在一天内对表1中前4个目标,或全部5个目标的访问,且当只有前4个目标时,设计轨道应为回归轨道。

表1 用户指定目标点的地心经、纬度Table 1 Longitudes and latitudes of user-specified target points

算例中动力学模型为非线性J2摄动模型,忽略其他摄动项的影响。轨道递推过程利用Runge-Kutta-Fehlberg (RKF78)数值计算得到,积分过程中相对误差和绝对误差(“RelTol”和“AbsTol”)都设置为10-12。

5.1 4个目标重复访问轨道设计

为实现4个地面目标重复访问,将轨道设置为天回归轨道,回归圈数的取值范围限制为N=8∶16,对应半长轴取值范围约为[RE+200 km,RE+4 200 km]。注意圈数取值过小会导致轨道半长轴过大。通过所提方法,遍历所有升、降轨和圈数组合后,共得到5组可行解,初始时刻对应的轨道参数如表2所示。在表2的访问弧段列中,Ak和Dk分别表示第k个目标在升轨段和降轨段访问。第一组解7天内的星下点轨迹如图3所示,图中五角星表示指定的地面目标点,可见设计轨道保持了良好的回归特性。

表2 4个地面目标重复访问轨道参数(回归周期1天)Table 2 Orbital elements for revisiting four ground target points (revisit period is one day)

图3 四个目标重复访问的星下点轨迹Fig.3 Ground tracks revisiting four ground target points

对于每组解,用户指定目标在第一天内的访问时刻以及对应的经度差如表3所示,其中Δtk=tk-t0为访问时刻与初始时刻的时间差,Δλk=λ(tk)-λk为访问时刻与目标点的经度差,k=1,2,3,…。由于航天器初始时刻在目标点1上方,其访问时刻和对应的经度差均为0。仿真结果表明,通过所提方法设计的轨道,其星下点轨迹能够准确经过指定的目标点,完成访问任务,访问时刻设计轨道和目标点之间的经度差不超过0.12°,该误差主要由线性和非线性J2模型之间的偏差导致。

表3 4个地面目标点的访问时刻及经度差Table 3 Visit moments and longitude difference for four ground target points

5.2 5个目标单次访问轨道设计

对于5个目标单次访问轨道设计,遍历所有升、降轨和圈数组合后,共得到3组解,初始时刻对应的轨道参数如表4所示。其中第二组解在一天内的星下点轨迹如图4所示。

表4 5个地面目标单次访问轨道参数Table 4 Orbital elements for a single visit to five ground target points

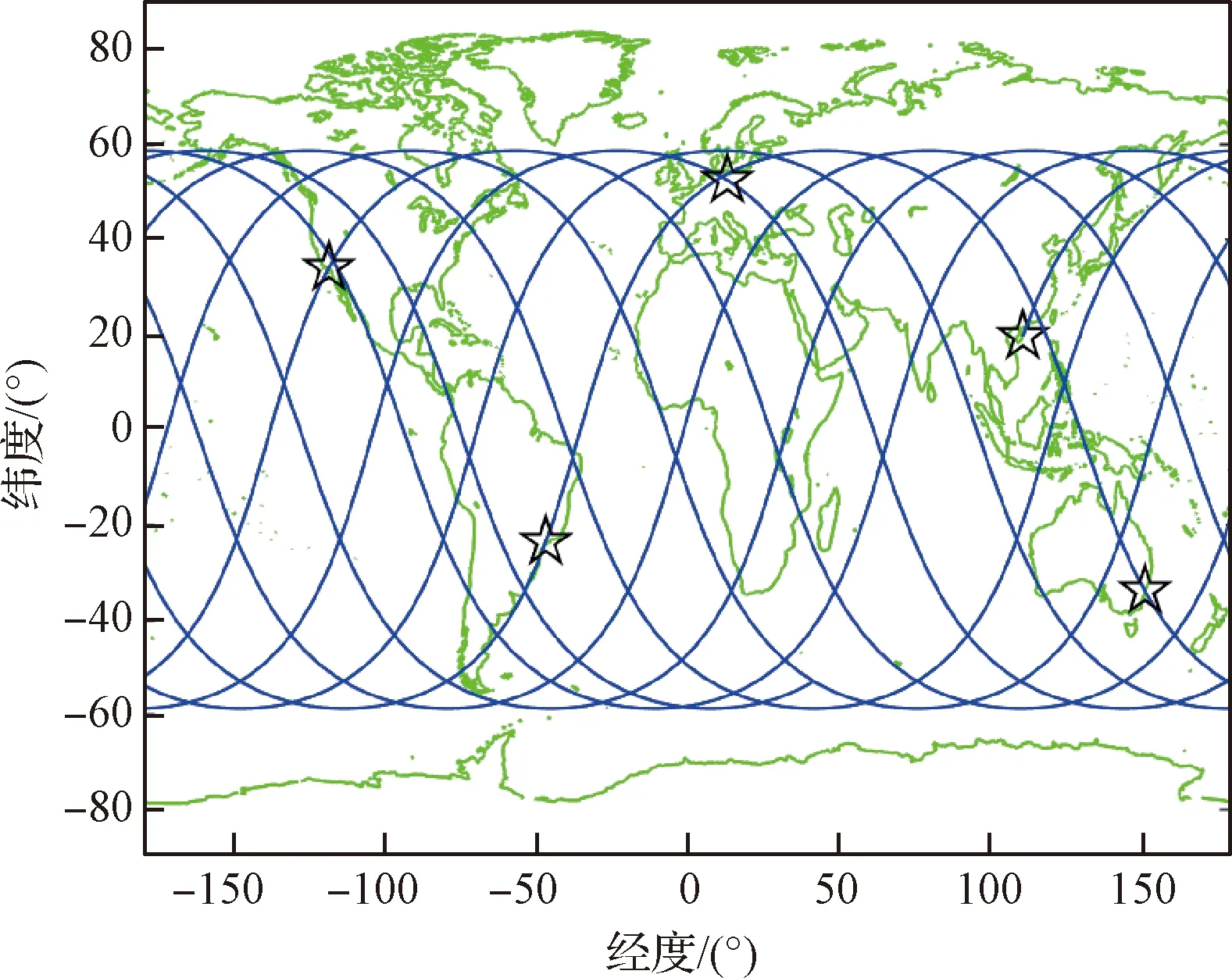
图4 5个目标单次访问的星下点轨迹Fig.4 Ground tracks for a single visit to five ground target points

对于每组解,用户指定目标点的访问时刻以及对应的经度差如表5所示。仿真结果表明,通过所提方法设计的轨道,其星下点轨迹能够在一天内精确经过指定的5个地面目标,完成访问任务,访问时刻设计轨道和目标点之间的经度差不超过0.09°,该误差同样主要由线性和非线性J2模型之间的偏差导致。

表5 5个地面目标点的访问时刻及经度差Table 5 Visit moments and longitude difference for five ground target points

5.3 随机目标点可行解的分布

对于4个目标点重复访问任务或5个目标点单次访问任务,由于约束方程个数和自变量个数相等,对于任意给定的目标点,可能存在无解的情况。本小节将在给定范围内随机选取4个或5个目标点,为上述两种任务各提供1 000次蒙特卡洛仿真,用以分析可行解存在的概率。

本小节将在表1中各目标经度±10°和纬度±10°的范围内随机选择新的目标点。任务初始时刻不变,所有目标点的访问时间仍限制在一天内,且遍历所有升、降轨和访问圈数组合。对于4个目标点重复访问任务,仍选择天回归轨道,回归圈数的取值范围限制为N=8∶16,对应轨道半长轴的取值范围约为[RE+200 km,RE+4 200 km]。两种任务在1 000次蒙特卡洛仿真中可行解的分布如图5所示。

图5 1 000次蒙特卡洛仿真中可行解的分布Fig.5 Distribution of feasible solutions in 1 000 times of Monte Carlo simulations

仿真结果表明,对于给定范围内随机指定的4个或5个目标点,两种任务无解的概率分别为13.7%和13.0%;大部分情况下可行解的个数在1到4个之间,概率分别为71.1%和81.2%。对于4个目标重复访问任务,有两个可行解的概率最大,为22.9%;对于5个目标单次访问任务,有一个可行解的概率最大,为27.0%。值得注意的是,若所有目标点均在某一集中区域内,受圈数限制,两种任务在一天内无解的概率会增大,此时可通过放宽访问时间要求(如可在两天或多天内实现全部访问)等来增大求解概率。

6 结 论

本文通过分析地面目标点访问约束和轨道参数之间的关系,给出了J2摄动下4个地面目标重复访问和5个地面目标单次访问轨道设计方法。在假设轨道倾角已知的前提下,其余5个轨道参数通过4个目标点的访问约束依次解析、或数值求解得到;然后利用回归约束或第5个目标点的访问约束,将轨道设计问题转换为只含有倾角的一维非线性方程,并通过数值方法求解。仿真算例表明,对于4个目标重复访问和5个目标单次访问轨道设计,均有离散的解,通过该方法设计轨道的星下点轨迹能够精确经过用户指定的目标点,访问时刻与目标点之间的经度差不超过0.12°,验证了方法的有效性。