海上浮标新型原子钟磁光阱数值模拟和参数优化

李嘉昕　陈海军　冯进军　吴启航

摘要：为了实现长时间实时采集并实时传输特定海域的海洋环境噪声、温度和深度等信息，需要提高浮标电子舱中原子钟自主守时的能力。本文基于蒙特卡洛方法对纵向冷却与推射分离的二维磁光阱（two-dimensinal magneto-optical trap with hollow cooling and pushing，2D-HP MOT）产生冷铯原子束的过程进行数值模拟。选取1×108个均匀分布且速度满足麦克斯韦-玻尔兹曼分布的原子，利用龙格-库塔法求解铯原子的运动方程，得到原子束通量和磁光阱系统各项参数的关系。对磁场梯度、蒸气压、横向冷却光、中空光的相关参数进行优化。模拟结果显示优化后的原子束通量达到3.1×1011个/s。该方法能够方便快捷地优化2D-HP MOT系统的参数，为新型浮标的工程化设计提供理论指导。

关键词：浮标； 磁光阱； 铯原子； 冷原子束

中图分类号：  U644.43+3文献标志码：  A

Numerical simulation and parameter optimization of novel

atomic clock magneto-optical trap for offshore buoys

LI Jiaxin1， CHEN Haijun1， FENG Jinjun1， WU Qihang2

（1. National Key Laboratory of Science and Technology on Vacuum Electronics，

Beijing Vacuum Electronics Research Institute， Beijing 100015， China;

2. Merchant Marine College， Shanghai Maritime University， Shanghai 201306， China）

Abstract： To realize the long-time real-time collection and real-time transmission of marine environmental noise， temperature and depth information in specific sea areas， it is necessary to improve the punctuality of the buoy electronic cabins atomic clock. Based on Monte Carlo method， the process of generating a cold cesium atomic beam by a two-dimensional magneto-optical trap with hollow cooling and pushing （2D-HP MOT） is numerically simulated. The hundred million uniformly distributed atoms with velocities satisfying the Maxwell-Boltzmann distribution are selected， and the equations of motion of the cesium atoms are solved by the Runge-Kutta method to obtain the relationships between the atomic flux and the parameters of the magneto-optical trap system. The parameters related to the magnetic field gradient， vapor pressure， transversely cooling beam， and hollow beam are optimized. The simulation results show that the optimized atomic flux reaches 3.1×1011 atoms/s. This method can conveniently and quickly optimize the parameters of the 2D-HP MOT system and provide theoretical guidance for engineering design of new buoys.

Key words： buoy; magneto-optical trap; cesium atom; cold atomic beam

0 引 言

近几年随着国际政治经济形势风云变幻和我国科技的高速发展，南海等海域大批GPS浮标全部更换成了北斗浮标，极大地提高了我国船舶的航运、航行安全性。不过现有的一些浮标确实存在如不能同步采集数据、传输慢、不守时等问题［1-2］。浮标电子舱由电池组和电子功能模块两部分组成，常开电源模块用来给系统值班控制电路和原子钟模块供电。原子钟模块在浮标系统下水前与北斗系统进行对时，一旦模块内部的自守时时间与北斗标准时间校准完毕，模块将依靠内部的原子钟补偿系统进行自守时，时间的保持能力小于1 ms。［3-4］

浮标电子舱原子钟模块充分利用了冷原子束具有的通量高、速度分布窄、横向速度小和准直性高等特性。冷原子束被广泛应用于原子频标［5-6］、玻色爱因斯坦凝聚（Bose-Einstein condensate，BEC）［7-8］、光谱学［9-10］等研究领域。磁光阱是实现中性原子冷却的重要手段，可以从气室里做无规则运动的原子中连续提取冷原子束。基于磁光阱技术的冷原子束源提取有多种不同的方案，例如二维磁光阱［11-12］（2D magneto-optical trap， 2D MOT）方案、增强型2D MOT（2D+ MOT）方案［13-14］、纵向冷却与推射分离的2D MOT（2D MOT with hollow cooling and pushing，2D-HP MOT）方案［15］等。2D MOT結构简单，采用四束横向的冷却光和四级型磁阱对原子进行横向冷却，在纵向（原子束出射方向）没有外加激光和磁场。SCHOSER等［12］利用该方案获得的铷原子束通量达到6×1010个/s，纵向平均速度为50 m/s，速度分布的半高全宽（full width at half maximum， FWHM）为75 m/s。2D+ MOT的磁场结构与2D MOT的基本一样，纵向增加冷却光能进一步降低原子束的速度。WANG等［13］采用2D+ MOT方案得到的铯原子束通量为3.6×1010个/s，纵向平均速度为7.3 m/s，FWHM为1 m/s。与2D+ MOT不同，2D-HP MOT在纵向使用同轴排布的中空冷却光和推射光，原子的纵向冷却由对射的中空光束实现，原子的推射由一束微弱的窄高斯光完成。黄家强［15］利用该方案得到的铯原子束通量达到2.6×1010个/s，纵向平均速度为6.8 m/s，FWHM为2.8 m/s，发散角为13×10-3 rad。

基于磁光阱技术产生的冷原子束具有连续性，应用于原子频标系统时，能够提高频标系统的频率稳定性。相较于其他磁光阱方案，2D-HP MOT采用独立调控的推射光控制冷原子的出射，通过减小推射光的功率降低纵向泄漏激光对频标系统造成的光频移，因此更适用于频标系统。在原子频标中，更高的原子束通量可以得到更高的信噪比，频率稳定度更高［16］。目前2D-HP MOT方案在原子束通量方面还有进一步提高的空间，因此通过优化该系统参数提高原子束通量具有重要的意义。

本文采用蒙特卡洛方法对浮标电子舱原子钟模块2D-HP MOT系统产生冷铯原子束的过程进行数值模拟，得到原子束通量随横向冷却光失谐量、磁场梯度变化的规律。着重分析中空光失谐量、中空光光强和蒸气压强对原子束通量的影响。根据模拟结果，优化2D-HP MOT各项参数提高原子束通量，并得到最佳参数下的原子束通量和纵向速度分布。

1 2D-HP MOT仿真模型

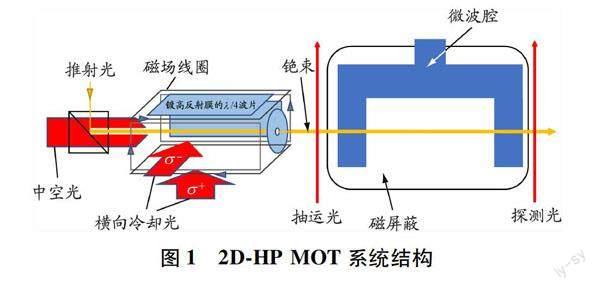
2D-HP MOT系统结构如图1所示，两对反亥姆霍兹线圈在横向（XY平面方向）产生梯度磁场，在纵向（Z方向）上的磁场强度为零。两对σ+-σ－组态的圆偏振光在横向上交汇形成冷却区域，其中σ+光可由σ－光经镀高反射膜的λ/4波片获得。在纵向上，镀高反射膜的λ/4波片中心有个小孔，中空光束经波片反射形成冷却光场，低速原子在推射光的作用下通过小孔形成原子束。铯原子的横向冷却由横向冷却光与梯度磁场构成的2D MOT完成。铯原子纵向冷却和推射分别由对射的中空光束和推射光实现，两束激光在空间上分离、互不干扰。

在数值模拟中，设定横向冷却光为45 mm×20 mm的矩形光束，频率负失谐于铯原子循环跃迁（62S1/2F=4→62S3/2F′=5）频率。设定中空光的参数：外径为15 mm，内径为4 mm，频率负失谐于铯原子循环跃迁频率。推射光的直径为3 mm，与循环跃迁频率共振。用于原子束出射的小孔直径设置为1 mm。

分别利用龙格-库塔法和解析解法求解该阻尼谐振子方程，结果如图2所示：时间步长为50 μs时，两种解法的结果存在偏差;时间步长为10 μs时，龙格-库塔法的计算结果是准确的，后续计算采用该时间步长。

在磁光阱中原子在从受力（式（11））减速到从小孔射出的过程中，可能会与背景气体中的高速原子碰撞而逃逸出阱。单位时间原子发生碰撞的概率［15］可以表示为

式中：vrms为背景气体中原子的均方根速度；σ为原子碰撞截面面积；nb为原子数密度；τ为阱中原子寿命；kB为玻尔兹曼常数;T为磁光阱内部的温度。

在模拟过程中，铯原子和激光每隔10 μs作用1次。原子运动至冷却区外则被视作原子与真空室壁发生碰撞，从而被从程序的模拟样本中去掉。在每个步长模拟中，需要根据原子的碰撞概率判断原子是否发生碰撞。原子在模拟时间为Δt时碰撞概率为pcoll=Δt/τ，并产生一个随机数ε∈（0，1），如果pcoll>ε则视作原子发生碰撞。当原子通过小孔后，即认为原子已经形成原子束从小孔射出，不再受激光作用。统计能够通过小孔形成原子束的原子数量，求出其占模拟样本数的比例η，计算出原子束通量［20］

3 模拟结果分析

考虑程序运行的时间和模拟结果的准确性，选择1×108个原子进行模拟。仿真综合考虑了磁场梯度、横向冷却光的失谐量、中空光的失谐量、中空光的光强、蒸气压等5项参数对原子束通量的影响，获得了各项参数的最优值。为了能够直观清晰地展现原子束通量与各项参数之间的关系，将模拟结果分为磁场梯度与通量的关系、横向冷却光失谐量与通量的关系、中空光参数和蒸气压与通量的关系等3个部分，交换各项参数的顺序对最终的优化结果没有影响。图3显示了原子束通量随磁场梯度的变化规律。随着磁场梯度增大，磁光阱阱深增加，俘获能力增强，原子束通量提高。当梯度过大时，只有离Z轴较近的原子能被减速，通量反而减少。为验证仿真结果的可靠性，与文献［21］的实验结果进行比较。该文献研究的是铷（Rb）原子，与本文模拟的铯原子能级不同，因此两者的最佳磁场梯度不同，但总体趋势一致。根据模拟结果，当磁场梯度为1×10-3 T/cm时原子束通量达到最大。

图4为原子束通量与横向冷却光失谐量的关系。模拟结果显示，当失谐量为-2.0Γ时原子束通量最大，原子束通量的变化趋势与文献［22］中的一致。该文献研究的是铯原子束，磁光阱结构与2D-HP MOT结构有所不同，但两者的最佳失谐量相差不大。模拟结果显示，当冷却光失谐量增大时，对应的磁光阱俘获速度增大，原子束通量增加。当冷却光失谐量超过-2.0Γ且继续增大时，散射力减小，原子束通量反而下降。

当推射光为共振光时，微弱的光强就能产生很高的原子束通量［12］。结合上述分析，当磁场梯度为1×10-3 T/cm，横向冷却光失谐量为-2.0Γ、光强为4 mW/cm2，推射光失谐量为0、光强为0.1 mW/cm2时，模拟得到中空光光强、中空光失谐量、蒸气压与原子束通量的关系，如图5所示。从图中可以看出，当蒸气压为6×10-5 Pa时，原子束通量较高，蒸气压继续增大会导致慢速原子与背景气体的碰撞概率增大，碰撞可能会导致被俘获的原子脱离原子束，从而使原子束通量下降。圖6为蒸气压为6×10-5 Pa时原子束通量与中空光光强的关系。模拟结果显示：原子束通量在中空光光强增大至5 mW/cm2时达到饱和;其后随着光强继续增大，原子束通量不会明显提高;在光强为5 mW/cm2、中空光失谐量为-2.5Γ时原子束通量最大。

根据优化的参数（磁场梯度为1×10-3 T/cm、蒸气压为6×10-5 Pa、横向冷却光失谐量为-2.0Γ、中空光失谐量为-2.5Γ、中空光光强为5 mW/cm2）模拟2D-HP MOT产生冷铯原子束的过程，见图7。一小部分原子在磁光阱的作用下聚集到中心线上，从小孔中出射形成原子束。图8为所得原子束的纵向速度分布的模拟结果，其速度分布可以用高斯线型拟合。原子束的平均纵向速度为8.0 m/s，FWHM为3.2 m/s，原子束通量达到3.1×1011个/s。优化原子束通量可以提高浮标电子舱原子钟模块的工作性能，使浮标系统与北斗系统的对时更加准确。

4 結 论

对浮标电子舱原子钟模块的2D-HP MOT制备冷铯原子束进行数值模拟，得到原子束通量与各项参数的关系，并通过优化设计参数使原子束通量能够达到1011数量级，从而进一步提高原子钟的频率稳定度。将模拟结果与相关文献的实验结果进行比较，验证了该数值模拟方法的准确性。通过模拟可以高效地对2D-HP MOT系统的各项参数进行优化，并提高浮标与原子钟补偿系统在测量海洋环境背景噪声时的自守时能力，对恶劣海况下新型浮标的工程化设计和仿真具有理论指导意义。

参考文献：

［1］陈新刚， 喻鹏， 刘大钢. 基于自持式剖面浮标的目标电场探测方法研究［J］. 中国造船， 2020， 61（增刊1）： 31-38.

［2］李松， 石敏， 栾经德， 等. 舰船轴频电场信号特征提取与检测方法［J］. 兵工学报， 2015， 36（增刊2）： 220-223.

［3］王科明， 韦俊霞. 一种海洋环境噪声测量浮标系统设计［J］. 声学与电子工程， 2017（4）： 13-15.

［4］孙强， 张伽伟， 喻鹏. 基于海洋浮标的电场干扰特性分析及信号检测方法［J/OL］. 兵工学报： 1-10（2022-07-14）.http：//kns.cnki.net/kcms/detail/11.2176.TJ.20220713.1743.004.html.

［5］DOMENICO G D， DEVENOGES L， JOYET A， et al. Uncertainty evaluation of the continuous cesium fountain frequency standard FOCS-2［C］//2011 Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum （FCS） Proceedings. IEEE， 2011： 1-5. DOI： 10.1109/FCS.2011.5977825.

［6］WANG H， IYANU G. MOT-based continuous cold Cs-beam atomic clock［C］//2010 International Frequency Control Symposium. IEEE， 2010： 454-458. DOI： 10.1109/FREQ.2010.5556290.

［7］LIN Y J， PERRY A R， COMPTON R L，et al. Rapid production of 87Rb Bose-Einstein condensates in a combined magnetic and optical potential［J］. Physical Review A， 2009， 79（6）： 063631. DOI： 10.1103/PhysRevA.79.063631.

［8］ROBERT A， SIRJEAN O， BROWAEYS A， et al. A Bose-Einstein condensate of metastable atoms［J］. Science， 2001， 292： 461-464. DOI： 10.1126/science.1060622.

［9］ANDEREGG L， AUGENBRAUN B L， BAO Y C， et al. Laser cooling of optically trapped molecules［J］. Nature Physics， 2018， 14： 890-893. DOI： 10.1038/s41567-018-0191-z.

［10］HOSTETTER J， PRITCHARD J D， LAWLER J E， et al. Measurement of holmium Rydberg series through magneto-optical trap depletion spectroscopy［J］. Physical Review A， 2015， 91： 012507. DOI： 10.1103/PhysRevA.91.012507.

［11］KELLOGG J R， SCHLIPPERT D， KOHEL J M， et al. A compact high-efficiency cold atom beam source［J］. Applied Physics B， 2012， 109： 61-64. DOI： 10.1007/s00340-012-5220-5.

［12］SCHOSER J， BATR A， LW R， et al. Intense source of cold Rb atoms from a pure two-dimensional magneto-optical trap［J］. Physical Review A， 2002， 66： 023410. DOI： 10.1103/PhysRevA.66.023410.

［13］WANG H， BUELL W F. Velocity-tunable magneto-optical-trap-based cold Cs atomic beam［J］. Journal of the Optical Society of America B， 2003， 20（10）： 2025-2030. DOI： 10.1364/JOSAB.20.002025.

［14］CHAUDHURI S， ROY S， UNNIKRISHNAN C S. Realization of an intense cold Rb atomic beam based on a two-dimensional magneto-optical trap： experiments and comparison with simulations［J］. Physical Review A， 2006， 74： 023406. DOI： 10.1103/PhysRevA.74.023406.

［15］黄家强. 冷铯原子微波频标新方案探索与研究［D］. 北京： 清华大学， 2016.

［16］王义遒， 王庆吉， 傅济时， 等. 量子频标原理［M］. 北京： 科学出版社， 1986： 318-322.

［17］JAMES F. Monte Carlo theory and practice［J］. Reports on Progress in Physics， 1980， 43： 1145. DOI： 10.1088/0034-4885/43/9/002.

［18］METCALF H J， VAN DER STRATEN P. Laser cooling and trapping［M］. Springer， 1999： 24-26.

［19］王义遒. 原子的激光冷却与陷俘［M］. 北京： 北京大学出版社， 2007： 295-297.

［20］WOHLLEBEN W， CHEVY F， MADISON K， et al. An atom faucet［J］.The European Physical Journal D， 2001， 15： 237-244. DOI： 10.1007/s100530170171.

［21］MLLER T， WENDRICH T， GILOWSKI M， et al. Versatile compact atomic source for high-resolution dual atom interferometry［J］. Physical Review A， 2007， 76： 063611. DOI： 10.1103/PhysRevA.76.063611.

［22］CAMPOSEO A， PIOMBINI A， CERVELLI F， et al. A cold cesium atomic beam produced out of a pyramidal funnel［J］， Optics Communications， 2001， 200： 231-239. DOI： 10.1016/S0030-4018（01）01643-1.

（編辑 贾裙平）

收稿日期： 2022-02-15

修回日期： 2022-10-18

作者简介： 李嘉昕（1998—），男，浙江台州人，硕士研究生，研究方向为量子频标器件，（E-mail）1245821291@qq.com；

陈海军（1979—），男，北京人，研究员，硕士，研究方向为量子频标器件，（E-mail）e1412225@163.com