基于Lyapunov理论考虑不确定扰动的船舶自适应跟踪控制

张强　李昊洋　孟祥飞　胡宴才　张树豪

摘要：针对受外界干扰的欠驱动船舶轨迹跟踪问题，提出一种自适应有限时间轨迹跟踪控制方法。通过设计自适应律逼近外部扰动的上界，结合有限时间控制理论设计轨迹跟踪控制律，再运用Lyapunov稳定性理论验证系统整体的稳定性。利用MATLAB进行对比仿真实验，验证此方法的有效性。实验结果表明：该控制方法的跟踪精度较高，跟踪误差较小，且可以快速收敛到一个零附近的有界区间，实现了欠驱动船舶有限时间的轨迹跟踪，为船舶安全航行和智能船舶研究提供参考。

关键词：欠驱动船舶； 轨迹跟踪； 有限时间； 自適应控制

中图分类号：  U664.82文献标志码：  A

Lyapunov theory-based adaptive tracking control for ships considering uncertain disturbances

ZHANG Qiang， LI Haoyang， MENG Xiangfei， HU Yancai*， ZHANG Shuhao

（School of Navigation and Shipping， Shandong Jiaotong University， Weihai 264200， Shandong， China）

Abstract： An adaptive finite time trajectory tracking control method is proposed to solve the trajectory tracking problem of underactuated ships affected by external interference. An adaptive law is designed to approximate the upper bound of external disturbances， the trajectory tracking control law is designed by the finite time control theory， and the Lyapunov stability theory is used to verify the stability of the overall system. The effectiveness of the method is verified by comparative simulation experiments using MATLAB. The experimental results show that， the tracking accuracy of the control method is higher， the tracking error is smaller， and it can quickly converge to a bounded interval near zero. It realizes the finite time trajectory tracking of underactuated ships， which provides reference for the safe navigation of ships and the research on intelligent ships.

Key words： underactuated ship; trajectory tracking; finite time; adaptive control

0 引 言

船舶轨迹跟踪控制是航海技术领域的一个重要研究方向。该研究不仅有助于推动船舶自动化、智能化的发展，而且能够提高船舶的航行安全，提升船舶运营效率，降低成本［1］。齐迹等［2］设计了船舶航向自适应控制器，解决了复杂环境下船舶航向保持控制效果差的问题，保证了航行安全。李轾［3］通过对全驱动系统与欠驱动系统的比较发现，虽然欠驱动系统设计复杂，但其诸多优势更适用于工程实践。当前船舶航行环境日益复杂，易产生船舶航迹偏离等问题，而船舶偏离预期的航迹可能导致运营效率降低或者发生碰撞危险［4-5］。控制船舶在有限时间内跟踪到预期轨迹，也是保障船舶航行安全的重要方面。王泰琪［6］设计了全驱动船舶的固定时间轨迹跟踪控制器，使船舶在短时间内跟踪到安全轨迹上。在船舶自动靠泊时，按照设计轨迹进行靠泊，不仅可以提高靠港效率而且可以降低碰撞码头的风险［7］。因此，研究欠驱动船舶自适应有限时间轨迹跟踪控制问题具有重要意义。

目前，科研工作者对欠驱动船舶的轨迹跟踪控制问题进行了大量研究。文献［8-11］指出实际的欠驱动系统需考虑所处环境的干扰以及动力学模型不匹配问题。为解决环境干扰问题，李荣辉等［12］设计了基于自抗扰控制的欠驱动船舶轨迹跟踪控制方案，通过仿真实验验证了方法的有效性。为解决动力学模型不匹配问题，李欧雪等［13］提出一种逆动力学自适应控制设计方法，解决了欠驱动船舶在非完整约束下和模型不匹配情况下的轨迹跟踪控制问题。QU等［14］为无人水面艇设计了一种指数跟踪控制方案，同时解决了环境干扰和系统不确定性问题。然而，上述对干扰处理的控制算法太过复杂。利用自适应控制解决干扰问题会更简便有效。张成举等［15］运用反步法，结合自适应控制，提出一种非线性鲁棒轨迹跟踪控制方法。DAI等［16］运用动态面方法，提出一种不确定扰动下船舶自适应神经网络跟踪控制方案。SUN等［17］利用比例积分滑模控制和反步法设计了一种鲁棒自适应轨迹跟踪法。刘杨［18］设计了一种以非线性混合神经网络来稳定自适应控制的方法。这些研究结合了自适应控制技术，但没有考虑到轨迹跟踪的时间问题。对于有限时间轨迹跟踪控制的研究，胡明月等［19］提出一种基于指令滤波器的有限时间轨迹跟踪控制方案，ZHU等［20］设计了一种输入饱和条件下基于单参数学习的欠驱动船舶有限时间跟踪控制方案。众多的欠驱动船舶轨迹跟踪控制研究表明，目前对船舶轨迹跟踪控制的限时问题关注较少。若能结合自适应控制，对欠驱动船舶在有限时间内进行轨迹跟踪控制，则可以大大提高船舶航行的效率并且减少事故的发生。

受以往研究成果启发，本文以欠驱动船舶自适应有限时间轨迹跟踪控制为研究点，与未采用有限时间控制的方案作对比。基于有限时间理论，设计控制律进行轨迹跟踪控制，并设计自适应律逼近干扰上界来抵抗干扰的影响，实现欠驱动船舶自适应有限时间轨迹跟踪控制。运用Lyapunov理论证明该控制系统的稳定性，通过仿真验证控制方案的合理性和有效性。

1 船舶运动数学模型

假定水面船舶处于xOy平面内，欠驱动船舶跟踪控制的三自由度数学模型［21］如下：

4 仿真研究

为验证设计的控制器在不同轨迹下的通用性和有效性，以挪威科技大学的Cybership 2船模作为被控对象，进行圆形和梯形两组仿真对比实验。该船总长L=1.255 m，质量m=23.8 kg，其他参数见文献［27］。

参考文献［24］中的仿真对比实验方法，将设计控制方案与未采用有限时间控制的方案进行仿真对比。对比方案的虚拟控制律、控制律和自适应律分别如下：

在模型参数mu、mv、mr均为未知的条件下，同时对设计控制律和对比控制律采用同样的模型参数和控制器系数，设置参数k11=0.1，k12=0.1，k21=0.2，k22=0.1，k31=0.2，k32=0.05，k41=0.4，k42=0.05，ω～u=0.01，ω～r=0.02，ζ=0.05，γu=0.1，λu=1，γr=0.01，λr=1。

在期望轨迹为参考轨迹的情况下，将有限时间设计控制律与未采用有限时间的对比控制律作对比。采用的期望圆形轨迹仿真方程如下：

圆形轨迹下，船舶的初始位置和初始速度为（x0，y0，ψ0，u0，v0，r0）=（0，10 m，0，0，0，0）。

船舶在平面内的圆形轨迹对比见图2。设计控制律的轨迹（实线）在坐标（19 m，9 m）附近跟踪上期望轨迹（虚线），而对比控制律的轨迹（点划线）在坐标（24 m，18 m）附近才跟踪上期望轨迹。在两种控制方案都跟踪上期望轨迹之后，设计控制律的轨迹更靠近期望轨迹，跟踪效果优于对比控制律。

对船体所处位置坐标（x，y）的跟踪情况见图3。在x轴方向上，两种控制律的曲线都在6 s左右跟踪上期望曲线，设计控制律的曲线更接近期望曲线。在y轴方向上，设计控制律的曲线在20 s左右跟踪上期望曲线，而对比控制律的曲线在40 s左右跟踪上期望曲线，设计控制律的曲线更贴近期望曲线。在设计控制律下，船舶在有限时间内跟踪上期望的位置，设计控制律的跟踪效果都更加接近期望，设计方案优于对比方案。

船舶在航行时的前向速度u和艏摇角速度r随时间变化的对比曲线见图4。对于前向速度u和艏摇角速度r，兩种控制律的跟踪曲线在50 s前都出现了较大波动，其原因是：轨迹跟踪是从船舶速度为零开始的，而开始时船舶速度是突变的。在50 s左右跟踪曲线趋于稳定，设计控制律的曲线比对比控制律的曲线更贴近期望曲线，设计控制律的跟踪效果更好。

跟踪轨迹的位置误差见图5。对于x轴跟踪误差，两种控制律的误差曲线都在25 s左右趋于稳定，稳定之后设计控制律的曲线更靠近零值（呈直线），误差不再变化，而对比控制律的误差在（-0.3 m，+0.3 m）范围内波动；对于y轴跟踪误差，对比控制律的曲线在60 s左右趋于稳定，设计控制律的曲线在25 s左右趋于稳定，曲线更靠近零值，误差更小；对于艏摇角跟踪误差，对比控制律的曲线在20 s左右趋于稳定，设计控制律的曲线在10 s左右趋于稳定，曲线更靠近零值，误差更小。跟踪轨迹的速度误差见图6：设计控制律的速度误差曲线波动更小，误差更接近零值。综上可知，设计控制律的跟踪效果更优。

控制输入的对比曲线见图7。两种控制律下的控制输入随着时间的变化都趋于有界，相较于设计控制律，对比控制律下的控制输入曲线有着更剧烈的波动。控制波动越剧烈，说明控制效率越低，因此设计控制律的控制性能更佳。

采用的梯形轨迹仿真方程如下：

梯形轨迹下，船舶的初始位置和初始速度为（x0，y0，ψ0，u0，v0，r0）=（0，10 m，0，0，0，0）。

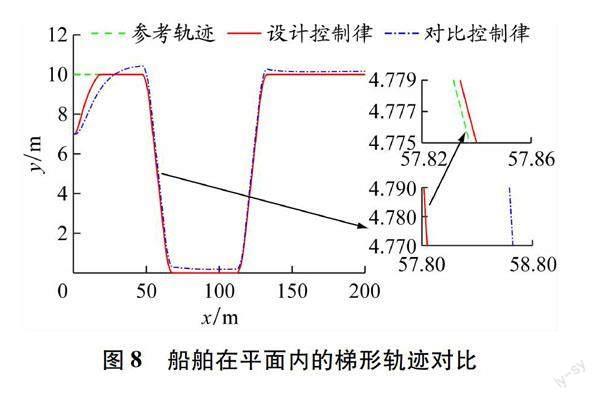
船舶在平面内的梯形轨迹对比见图8。设计控制律的轨迹（实线）在坐标（15 m，10 m）附近跟踪上期望轨迹（虚线），而对比控制律的轨迹（点划线）在坐标（50 m，10 m）附近才跟踪上期望轨迹。当两种控制律都跟踪上期望轨迹后，设计控制律的轨迹更靠近期望轨迹，跟踪效果相较于对比控制律的更好。

对船体所处位置的坐标（x，y）跟踪情况见图9。在x轴方向上，两种控制律的曲线几乎都在0 s跟踪上期望曲线，设计控制律的曲线更接近期望曲线；在y轴方向上，设计控制律的曲线在20 s左右跟踪上期望曲线，而对比控制律的曲线在50 s左右跟踪上期望曲线，且设计控制律的曲线更贴近期望曲线。设计控制律下的船舶可以在有限时间内跟踪上期望的位置，设计控制律的跟踪效果更加接近期望，表明设计控制律的跟踪效果更佳。

船舶在航行时的前向速度u和艏摇角速度r随时间变化的对比曲线见图10。对于前向速度u和艏摇角速度r，两种控制律的曲线都在5 s左右跟踪上期望曲线；对比两种控制律下的跟踪曲线，设计控制律的跟踪曲线比对比控制律的跟踪曲线更贴近期望曲线，设计控制律的跟踪效果更好。

跟踪轨迹的位置误差见图11。对于x轴跟踪误差：对比控制律的曲线在40 s左右趋于稳定，设计控制律的曲线在20 s左右趋于稳定；稳定之后设计控制律的曲线呈直线，误差不再变化，且误差更小，而对比控制律的误差曲线还存在极小的波动。对于y轴跟踪误差，对比控制律的曲线在50 s左右趋于稳定，设计控制律的曲线在20 s左右趋于稳定，曲线更靠近零值，跟踪精度更高。对于转艏角跟踪误差，对比控制律的曲线在10 s左右趋于稳定，设计控制律的曲线在5 s左右趋于稳定，误差更小。跟踪轨迹的速度误差见图12。设计控制律的速度误差曲线波动更小，误差更接近零。综上可知，设计控制律的跟踪效果更好。

控制输入的对比曲线见图13。两种控制律下的控制输入随着时间的变化都趋于有界，相较于设计控制律，对比控制律的控制输入曲线有着更剧烈的波动。控制波动越剧烈，说明控制难度越高，控制效率越低，因此设计控制律的控制性能更佳。

由两组仿真实验的结果可知：设计的有限时间轨迹跟踪控制方案在不同的跟踪轨迹下，在各方面都表现出了良好的性能；设计控制律的各参数曲线都能比对比控制律的更早跟踪上期望曲线，误差更稳定，误差范围更小；设计方案相较于未采用有限时间控制的方案具有更多的优势。

5 结论与展望

针对欠驱动船舶提出一种考虑外界干扰的自适应有限时间轨迹跟踪控制方法。首先，通过设计自适应律对外部干扰的最大估计值进行逼近，设计控制律使轨迹跟踪的各参数误差趋于零；然后，运用Lyapunov稳定性理论证明系统稳定性；最后，对两组不同轨迹进行仿真实验，结果表明船舶轨迹跟踪误差和速度跟踪误差收敛速度更快，误差收敛到接近于零的一个极小的范围内（可以忽略不计），验证了该控制系统的有效性，即能够保证实际航行中的欠驱动船舶在有限时间内跟踪上期望轨迹。当前全球船舶数量急剧增加，自适应有限时间控制方案不仅可以运用于自动靠泊解决航道拥堵问题，还可以运用于船舶避碰，从而减少事故的发生。目前对船舶控制的研究大部分直接针对船舶行驶时的推进力和转弯扭矩，后续研究拟将螺旋桨和舵机的传动模型结合到推进力和转弯扭矩的设计中，以便该方法的推广应用。

参考文献：

［1］蒲进菁， 刘涵， 江云华， 等. 无人船现状及发展趋势综述［J］. 海洋信息， 2020， 35（1）： 6-11. DOI： 10.19661/j.cnki.mi. 2020.01.002.

［2］齐迹， 李建民， 李伟. 船舶航向自适应控制系统研究［J］. 航海技术， 2022， 44（1）： 37-41.

［3］李轾. 两种欠驱动系统的非线性控制方法研究［D］. 济南： 山东大学， 2020.

［4］冯哲， 张燕菲. 基于PID算法的船舶航迹自动控制方法［J］. 舰船科学技术， 2018， 40（6A）： 34-36. DOI： 10.3404/j.issn.1672-7649.2018.6A.012.

［5］陈延辉， 宫蕾. 先验地理信息辅助下船舶避碰轨迹规划模型构建［J］. 舰船科学技术， 2021， 43（8A）： 22-24. DOI： 10.3404/j.issn.1672-7649.2021.8A.008.

［6］王泰琪. 全驱动船舶固定时间轨迹跟踪控制方法研究［D］. 哈尔滨： 哈尔滨工程大学， 2019.

［7］刘新召. 基于最优轨迹规划的船舶自动靠泊控制研究［D］. 大连： 大连海事大学， 2020.

［8］FOSSEN T I， BERGE S P. Nonlinear vectorial backstepping design for global exponential tracking of marine vessels in the presence of actuator dynamics［C］//Proceedings of the 36th Conference on Decision and Control. IEEE， 1997， 5： 4237-4242. DOI： 10.1109/CDC.1997.649499.

［9］DU J L， HU X， KRSTIC＇ M， et al. Dynamic positioning of ships with unknown parameters and disturbances［J］. Control Engineering Practice， 2018， 76： 22-30. DOI： 10.1016/j.conengprac.2018.03.015.

［10］李宗宣， 卜仁祥， 范藝. 结合速度和干扰观测的船舶路径跟踪模型预测控制［J］. 上海海事大学学报， 2021， 42（1）： 19-25. DOI： 10.13340/j.jsmu.2021.01.004.

［11］秦朝宇， 李伟， 宁君， 等. 基于非奇异终端滑模的船舶航迹跟踪自抗扰控制［J］. 上海海事大学学报， 2016， 37（3）： 13-17. DOI： 10.13340/j.jsmu.2016.03.003.

［12］李荣辉， 李铁山， 卜仁祥. 欠驱动水面船舶航迹跟踪自抗扰控制［J］. 大连海事大学学报， 2013， 39（2）： 5-8.

［13］李欧雪， 周宇生. 欠驱动无人船的运动控制设计［J］. 重庆工商大学学报（自然科学版）， 2021， 38（4）： 23-29. DOI： 10.16055/j.issn.1672-058X.2021.0004.004.

［14］QU Y H， XIAO B， FU Z Z， et al. Trajectory exponential tracking control of unmanned surface ships with external disturbance and system uncertainties［J］. ISA Transactions， 2018， 78： 47-55. DOI： 10.1016/j.isatra.2017. 12.020.

［15］张成举， 王聪， 曹伟， 等. 欠驱动USV神经网络自适应轨迹跟踪控制［J］. 哈尔滨工业大学学报， 2020， 52（12）： 1-7. DOI： 10.11918/201905049.

［16］DAI S L， HE S D， LIN H. Transverse function control with prescribed performance guarantees for underactuated marine surface vehicles［J］. International Journal of Robust and Nonlinear Control， 2019， 29（5）： 1577-1596. DOI： 10.1002/rnc.4453.

［17］SUN Z J， ZHANG G Q， QIAO L， et al. Robust adaptive trajectory tracking control of underactuated surface vessel in fields of marine practice［J］. Journal of Marine Science and Technology， 2017， 23： 950- 957. DOI： 10.1007/s00773-017-0524-0.

［18］刘杨. 欠驱动水面船舶的非线性自适应控制研究［D］. 大连： 大连海事大学， 2010.

［19］胡明月， 于双和， 李云云， 等. 基于指令滤波的全状态约束海洋水面船舶有限时间轨迹跟踪控制［J］. 南京理工大学学报， 2021， 45（3）： 271-280. DOI： 10.14177/J.CNKI.32-1397N.2021.45.03.003.

［20］ZHU G B， MA Y， HU S L. Single-parameter-learning-based finite-time tracking control of underactuated MSVs under input saturation［J］. Control Engineering Practice， 2020， 105： 104652. DOI： 10.1016/j.conengprac.2020.104652.

［21］DENG Y J， ZHANG X K， IM N， et al. Model-based event-triggered tracking control of underactuated surface vessels with minimum learning parameters［J］. IEEE Transactions on Neural Networks and Learning Systems， 2019， 31（10）： 4001-4014. DOI： 10.1109/TNNLS.2019.2951709.

［22］WANG F， CHEN B， LIU X P， et al. Finite-time adaptive fuzzy tracking control design for nonlinear systems［J］. IEEE Transactions on Fuzzy Systems， 2017， 26（3）： 1207-1216. DOI： 10.1109/TFUZZ.2017.2717804.

［23］HUANG Y， JIA Y M. Adaptive fixed-time six-DOF tracking control for noncooperative spacecraft fly-around mission［J］. IEEE Transactions on Control Systems Technology， 2018， 27（4）： 1796-1804. DOI： 10.1109/TCST. 2018.2812758.

［24］ZHANG Q， ZHANG M J， YANG R M， et al. Adaptive neural finite-time trajectory tracking control of MSVs subject to uncertainties［J］. International Journal of Control Automation and Systems， 2021， 19（6）： 2238-2250. DOI： 10.1007/s12555-020-0130-5.

［25］POLYCARPOU M M. Stable adaptive neural control scheme for nonlinear systems［J］. IEEE Transactions on Automatic Control， 1996， 41（3）： 447-451. DOI： 10.1109/9.486648.

［26］吴文涛， 古楠， 彭周华， 等. 多领航者导引无人船集群的分布式时变队形控制［J］. 中国舰船研究， 2020， 15（1）： 21-30. DOI： 10.19693/j.issn.1673-3185.01734.

［27］SKJETNE R， FOSSEN T I， KOKOTOVIC＇ P V. Adaptive maneuvering with experiments for a model ship in a marine control laboratory［J］. Automatica， 2005， 41： 289-298. DOI： 10.1016/j.automatica.2004.10.006.

［28］張强. 船舶自动靠泊简捷非线性鲁棒控制［D］. 大连： 大连海事大学， 2018.

（编辑 贾裙平）

收稿日期： 2021-10-15

修回日期： 2022-04-14

基金项目： 国家自然科学基金（51911540478）；山东省重点研究发展计划（2019JZZY020712）；山东省研究生教育教学改革研究项目（SDYJG19217）；山东交通学院博士生科研创业基金及山东交通学院攀登研究创新团队计划（SDJTUC1802）

作者简介： 张强（1982—），男，山东潍坊人，船长，教授，博士，研究方向为船舶、机器人运动与控制，（E-mail）zq20060054@163.com

*通信联系人。（E-mail）yancaihu@126.com