模型与数据双驱动的失眠脑电alpha节律研究

李 强,潘 敏,成 波

(1.安康学院 数学与统计学院,陕西 安康 725000;2.西北大学 医学大数据研究中心,陕西 西安 710127)

睡眠是诸多脑功能状态中的一种,是指大脑意识相对丧失、自主的肌肉活动消失、受适当刺激可完全恢复到清醒时的生理功能的一种自主行为[1]。睡眠占据了人一生近1/3的时间,在生理功能调节、记忆巩固、脑内代谢物清除以及生长发育等方面起着至关重要的作用。良好的睡眠有助于人们提高工作和学习效率,保持身心健康。根据R-K睡眠评估准则[2],睡眠状态主要分为非快速眼动状态(non-rapid eye movement,NREM)和快速眼动状态(rapid eye movement,REM)。两种状态下大脑的放电活动是截然不同的,表现为脑电节律之间存在的显著差异(见表1)。这些脑电节律的正常发放有助于维护睡眠稳定性[3-5]。

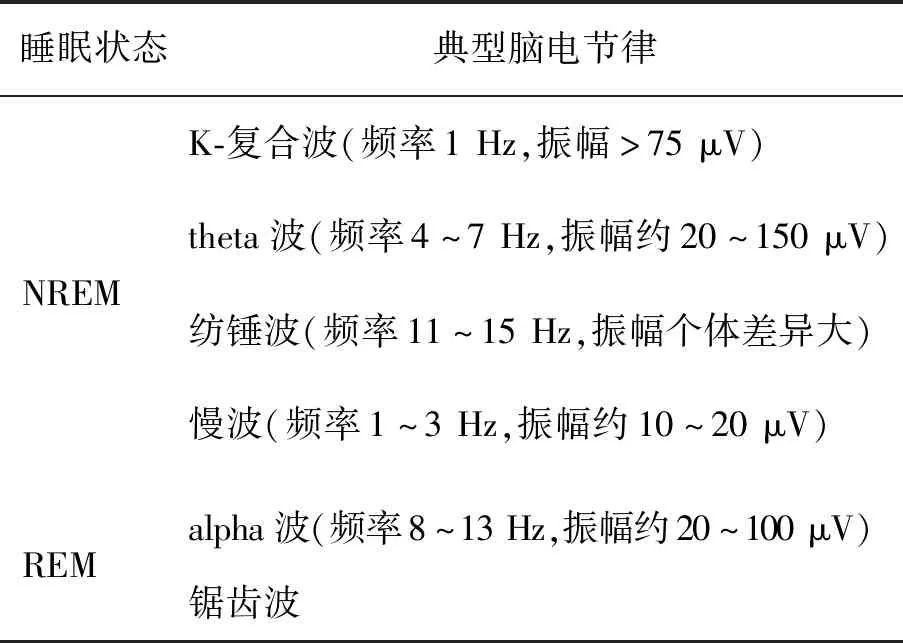
表1 NREM状态和REM状态分别对应的典型脑电节律Tab.1 The typical EEG rhythms during NREM and REM

睡眠障碍是指睡眠量和质的异常,或在睡眠过程中发生某些临床症状(如梦行症)[6]。失眠是最常见且发病率极高的一种睡眠障碍,以入睡困难、睡眠维持困难及早醒等为主要特征,且每周至少发生3次并持续3个月以上[7]。尽管失眠在短期内不会直接威胁到人们的生命安全,但如果任由病情发展,会给患者带来一系列并发疾病(如精神类疾病、心脑血管疾病、代谢性疾病等),甚至导致死亡。研究表明,临床上一些失眠患者在睡眠REM阶段,会出现明显的脑电alpha节律活动增强现象[8]。这一发现对于通过调节alpha节律的发放来控制失眠患者的病情发展具有重要的指导意义。然而,关于这一现象发生的内在机制目前尚不清楚。

作为一类基于生物物理基础的数学模型,神经计算模型(neural computational model,NCM)为探索、解释及验证大脑内各类生理病理现象的内在机制提供了一种有效途径[9]。NCM主要采用数学理论与方法对大脑内在生理病理机制进行建模,进而通过神经环路重建的方式来模拟电信号的产生、演变及传导等神经活动过程。神经集群模型是一类应用极为广泛的宏观神经计算模型,它将功能相似、结构相近的神经元看作为一个整体(即神经元集群),并通过描述神经元集群的平均特性来反映其整体放电行为[10-11]。典型的神经集群模型包括Jansen模型[12]、Wendling模型[13]、Liley模型[14]、Suffczynski模型[15]等。其中,Liley模型结构简单且已成功应用于模拟NREM与REM睡眠状态转迁及对应的脑电节律[16-17]。

鉴于上述分析,本文将从计算神经科学的角度出发,结合Liley神经计算模型与临床失眠脑电数据,探索失眠患者在REM期典型放电节律的发生机制。首先,设计一种基于马尔可夫蒙特卡洛的Liley模型关键参数的自动选择与估计方法;其次,结合失眠患者脑电数据,确定影响alpha节律发放的模型关键参数,并据此给出失眠患者REM期脑电alpha节律活动增强的机制假设。

1 Liley神经计算模型

2002年,Liley等人通过考虑大脑皮层上神经元之间的兴奋性与抑制性连接,提出了一个用于研究哺乳动物大脑电活动中alpha节律发放机制的神经计算模型(简称为Liley模型)。本节将对Liley模型的拓扑结构与数学建模过程进行概述。

Liley模型包括两个神经元集群:兴奋性神经元集群(E)与抑制性神经元集群(I),其拓扑结构如图1所示。其中,集群E与I之间存在相互作用,且均存在自反馈作用以及来自丘脑的外部输入(分别记为Pee、Pei)。图1中黑色实线箭头表示由兴奋性神经递质谷氨酸AMPA受体所介导的兴奋性投射作用;黑色实线圆点表示由抑制性神经递质γ氨基丁酸GABA受体所介导的抑制性投射作用。

图1 Liley模型的拓扑结构Fig.1 The topological structure of Liley model

Liley模型的数学建模过程主要从以下3个方面来阐述。

1)突触后膜电位的数学刻画。

突触后膜电位I(t)由突触响应函数h(t)与突触传入的兴奋性和抑制性脉冲(采用平均脉冲发放速率Q(t)刻画)的卷积得到,即

(1)

式中:

h(t)=Γγ·te1-γt,t≥0

(2)

式中:Γ表示突触后膜电位的最大幅值;γ表示突触后膜电位的指数衰减时间尺度。

(3)

进一步,可转化为如下二阶微分方程来进行求解

(4)

2)胞体膜电位的数学刻画。

采用突触后膜电位I(t)的加权和刻画胞体膜电位V(t),即

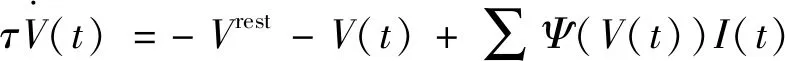
(5)

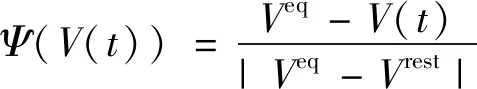
3)平均脉冲发放速率的数学刻画。

由Sigmoid函数S(·)作用于胞体膜电位V(t),则可得平均脉冲发放速率Q(t),即

(6)

式中:Qmax为集群的最大脉冲发放速率;θ为发放阈值;σ为Sigmoid函数的梯度。

Liley模型中电活动的传导过程主要由两个计算模块来完成:“平均脉冲发放速率-胞体膜电位”计算模块(记为Q-V)与“胞体膜电位-平均脉冲发放速率”计算模块(记为V-Q),如图2所示。在第1个计算模块中(蓝色虚线),脉冲输入Q(t)基于式(4)转换为突触后膜电位I(t),然后由式(5)得到胞体膜电位V(t);在第2个计算模块中(红色虚线),胞体膜电位V(t)基于式(6)转换为平均脉冲发放速率Q(t)。

图2 Liley模型中电活动的传导过程Fig.2 The detailed transformation of electrical activities in Liley model

Liley模型的数学表达见式(7),模型输出为兴奋性神经元集群的胞体膜电位Ve。Liley模型中所有参数的生理学含义、参考取值及单位见表2[14,18-19]。

Γeγeee(NeeSe(Ve)+Pee(t)),

Γiγiee(NieSi(Vi)+Pie(t)),

Γeγeie(NeiSe(Ve)+Pei(t)),

Γiγiie(NiiSi(Vi)+Pii(t))

(7)

表2 Liley模型的参数取值及其生理学含义Tab.2 The parameters of Liley model and their physiological description

2 模型关键参数的自动选择与估计方法

在Liley模型中,对模型行为影响较大的参数称为模型关键参数。如何从众多模型参数中自动选择出关键参数并对其进行分析,显然对于理解模型行为具有重要意义。本节给出一种数据驱动的模型关键参数的自动选择与估计方法,具体步骤可总结为如下算法1。

算法1给定脑电信号S,记θ=(θ1,θ2,…,θN)为模型参数,其中N为参数的总个数。

记π(θj)(j=1,2,…,N)为第j个参数的先验分布,采用马尔科夫蒙特卡洛算法估计参数θj的后验分布,即

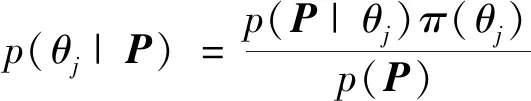
(8)

其中

(9)

式(8)～(9)的更多细节可见文献[19-20]。

步骤2选择模型关键参数。首先,针对每一参数θj,计算其后验样本的均方根偏差

(10)

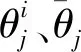
进一步,为了比较不同参数样本内部的离散程度,计算参数θj后验样本的相对均方根偏差

(11)

式中:θjmax、θjmin分别表示参数θj可取的最大值与最小值。显然,RRMSDθj的值越小,参数θj后验分布范围相对更集中,即从脑电数据S中所获得的信息越多。

(12)

3 实验结果及分析

3.1 脑电数据集

本文所使用的脑电数据来自于Kermanshah医科大学睡眠障碍研究中心临床采集的失眠脑电数据集[21]。该数据集的具体信息见表3。

上述数据集中,每30 s脑电片段的睡眠状态评估结果均由睡眠专家根据AASM准则[22]进行了标注。针对健康受试者与失眠患者,分别随机选取450个REM睡眠期的30 s单通道脑电片段,并计算其功率谱。所选脑电通道为F4[23]。图3(a)和图3(b)分别展示了所选健康受试者和失眠患者的脑电片段对应的频谱图。从图中黑色椭圆圈标记处可以看出,相比于健康受试者,失眠患者脑电alpha节律所在频段(8～13 Hz)对应的功率谱值较大,这也验证了失眠患者REM期脑电alpha节律活动增强的结论。

图3 不同受试者脑电片段的频谱图Fig.3 The EEG spectrograms of different subjects

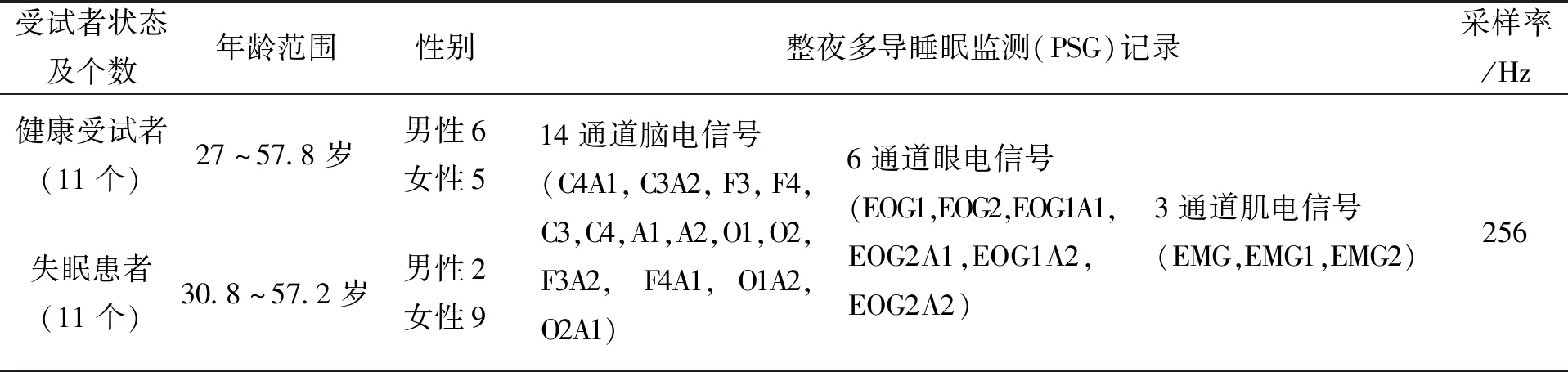
表3 Kermanshah医科大学睡眠障碍研究中心临床采集的失眠脑电数据集的具体信息Tab.3 Detail information of EEG data from the Sleep Disorder Research Center in Kermanshah University of Medical Sciences

3.2 影响脑电alpha节律活动的模型关键参数选择及其分析

本小节基于上述所得脑电片段的功率谱,结合本文所提算法1,确定影响脑电alpha节律活动的模型关键参数及其最优取值。

首先,以一个脑电片段为例对以上过程进行说明。图4(a)展示了来自“失眠患者1”的REM期10 s脑电片段,主要表现为alpha节律的发放。采用该脑电片段估计Liley模型中22个参数的后验分布,并对每个参数后验分别计算相对均方根偏差(RRMSD)。进而对RRMSD按照从小到大的顺序进行排序,并选择排序前5%(这里将算法1中的参数q%设置为5%)的参数作为模型关键参数。图5展示了所得的参数后验分布(红色)、先验分布(蓝色)及参数后验样本的RRMSD。从图中紫色椭圆圈标记处可以看出,参数γi后验分布范围相对更小,对应的RRMSD值最小(RRMSDγi=0.012)。由此说明,参数γi从该数据中获得了更多信息,对于调节alpha节律活动具有重要作用,即为模型关键参数。

其次,随机选取80个来自失眠患者的REM期30 s脑电片段,计算所有模型参数后验样本的RRMSD值,所得结果如图6所示。可以看出,相比于其他参数,参数γi后验样本的RRMSD值整体较小(图中红色框标记处所示)。由此可见,参数γi确为对脑电alpha节律活动影响最大的关键参数。结合其生理学含义,可以得出:抑制性突触活动强度的变化可以影响失眠患者脑电alpha节律活动。

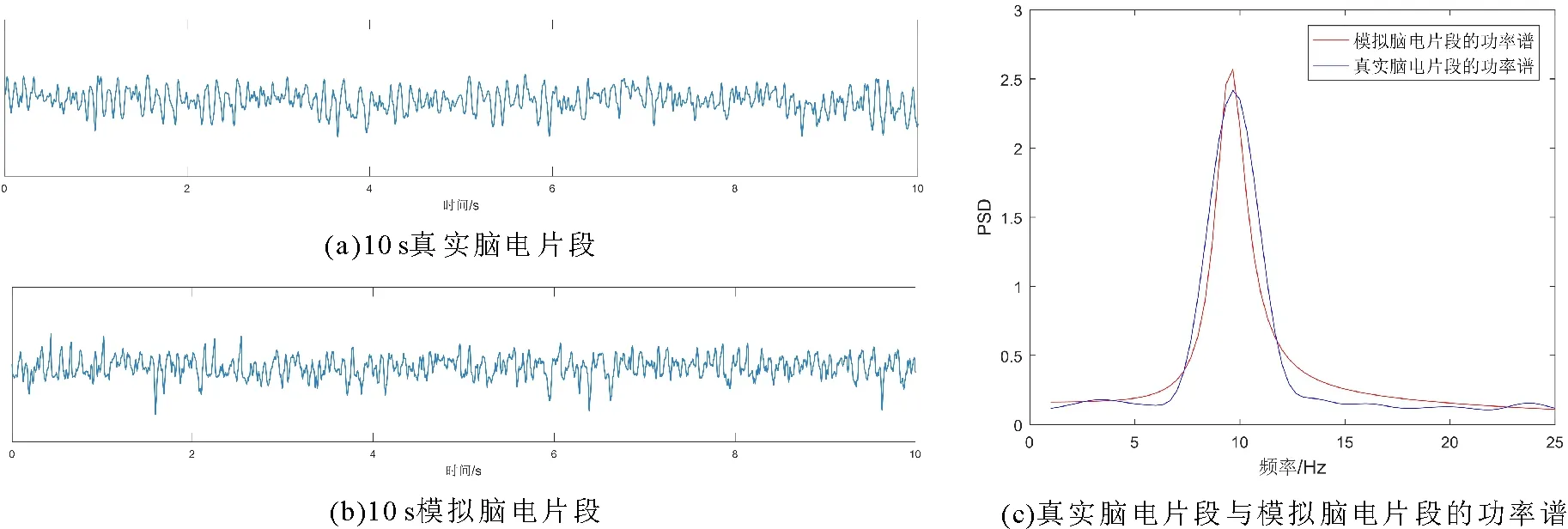
图4 脑电片段及功率谱Fig.4 The EEG segments and power spectra

图5 模型参数的后验分布(红色)、先验分布(蓝色)及参数后验样本的相对均方根偏差(RRMSD)Fig.5 The posterior (red color) and prior marginal (blue line) distributions of each model parameter and the RRMSD values of parameter posterior samples

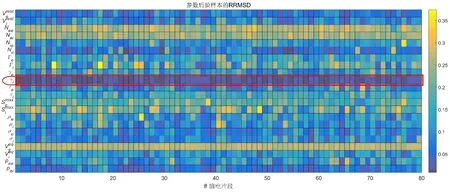
图6 80个脑电片段对应的参数后验样本的相对均方根偏差(RRMSD)Fig.6 The RRMSD values of parameter posterior samples obtained from 80 EEG segments

3.3 失眠患者脑电alpha节律活动增强的机制假设

本小节面向健康受试者与失眠患者,分别根据其脑电片段估计对应的参数γi最优取值,并据此分析比较二者之间的差异性,进而给出失眠患者脑电alpha节律活动增强的一种机制解释。

随机选取80个来自健康受试者的REM期30 s脑电片段以及80个来自失眠患者的REM期30 s脑电片段。图7展示了由这些脑电片段所得到的参数γi最优取值的箱线图。从图中可以看出,相比于健康受试者,由失眠患者脑电片段得到的参数最优值整体偏高,即抑制性突触后膜电位的衰减速率是增加的,进而抑制性突触活动的强度是下降的。基于此,本文给出一种机制假设:抑制性突触活动强度的降低可诱导失眠患者REM期脑电alpha节律活动的增强。

图7 参数γi最优估计值的箱线图(由健康受试者与失眠患者脑电数据确定)Fig.7 Box plots of the optimized values of parameter γi(obtained from EEG data of healthy subjects and patients with insomnia)

4 结语

本文从计算神经科学的角度出发,结合Liley神经计算模型与临床失眠脑电数据,对失眠患者REM期脑电alpha节律活动增强现象进行了内在机制上的解释。具体地,设计了一种基于马尔可夫蒙特卡洛的Liley模型关键参数的自动选择与估计方法;采用临床采集的失眠患者脑电数据,通过数值实验验证了所提方法的有效性,确定了影响alpha节律发放的模型关键参数,并据此给出了失眠患者REM期脑电alpha节律活动增强的机制假设:抑制性突触活动强度的降低会诱导alpha节律活动的增强。所得结论对于通过调节alpha节律的发放来改善失眠患者睡眠质量并控制病情发展,具有一定的指导作用和临床价值。