半区间上 D.H.Lehmer问题余项的一种均值
2023-06-21刘晓莹徐哲峰
刘晓莹,徐哲峰
(西北大学 数论及其应用研究中心,陕西 西安 710127)
设q>2和a是两个整数,且(a,q)=1。对每一个满足1≤b≤q的整数b,存在唯一的c满足
对于q=p为奇素数和a=1,D.H.Lehmer建议研究Q(1,p)的值或者至少给出它的一些非平凡结论[1]。对D.H.Lehmer提出的问题,Zhang W P[2]证明了
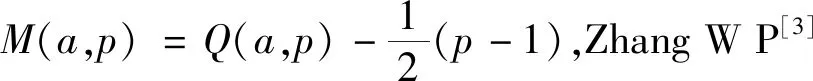
Xu Z F等[4]研究了余项M(a,p)的一种均值,证明了下面的渐近公式
而如果非负整数s≠2,3,4,有
由此揭示了完整区间上D.H.Lehmer问题,即经典D.H.Lehmer问题余项相消性随参数s的不同有着非常显著的变化。
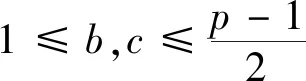
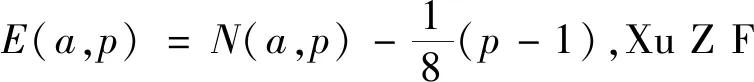
与文献[4]中关于完整区间上D.H.Lehmer问题余项类似,本文讨论半区间上D.H.Lehmer问题余项的一种均值,给出了定理1。
定理1设p≥3为素数,则有渐近公式
对于非负整数s≠0,1,3,4,有
其中,Ο常数只依赖于任意小的正数ε,而Οε常数依赖于ε和s。
从定理1的结论来看,对于不同的参数s,半区间上D.H.Lehmer问题余项的这种双参数均值的主项各不相同,但均不为0。而文献[4]中对于完整区间上D.H.Lehmer问题余项的相同形式的均值仅在s=2,3,4时其主项不为0,s取其他非负整数时主项均为0。从这些结论可以看出,这两种区间上D.H.Lehmer问题余项的相消性有显著的差异。
1 若干引理
为方便定理1的证明,本节先给出7个引理。
引理1设p为奇素数,则对满足(a,p)=1的任意正整数a,有
E(a,p)=
式中
证明过程可参考文献[6]中的引理7.1。
引理2设p为素数,m≥0为任意给定的整数,则有
和
证明过程可参考文献[6]中的引理4.3。
引理3设q>4为一个奇数,χ为模q的原特征且满足χ(-1)=-1。则有
证明过程可参考文献[6]中的引理1.6。
引理4设q≥5为奇整数,χ为模q的原特征且满足χ(-1)=1,则下述等式成立。
式中,χ4表示模为4的原特征。
证明过程可参考文献[6]中的引理1.4。
引理5设q和r是满足q≥2和(r,q)=1的整数,有如下性质
和
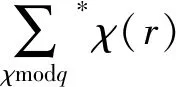
证明过程可参考文献[7]中的引理 3。
引理6设q>2为奇整数,m≥0为一个给定的整数,则对任意满足Res>1的复变量s,有恒等式
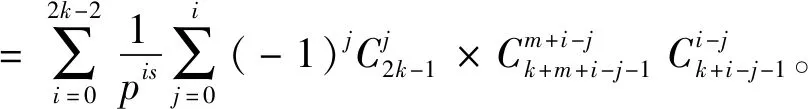
证明过程可参考文献[6]中的引理2.5。
引理7设q>2为奇整数,χ为模q的特征,χ4表示模为4的原特征,则下述渐近公式成立。
特别地,当q=p为素数且k=2时,有
和
证明设τk(n)[8-10]表示k次除数函数(即方程n1,n2,…,nk=n的所有正整数解的个数),则对任意参数q≤N M1+M2+M3+M4 (1) 分别估计式(1)中的每一项,利用引理5可得 则有 对前面3种情形,有估计式 及 结合引理6,可以得到 因为(q,2)=1, 所以有 Οs(qε) (2) 类似地,可得 (3) 则从式(1)~(3)可以得到 (4) 结合估计[11] 由Cauchy不等式,可得 则有 类似地,有 引理7得证。 首先,利用引理1~4,可得 (2+χ(2)-χ(4))2× Ο(p)。 当s≥6时, Ο(p)。 注意到 其次,利用引理2和引理7,则有 当s=3时,有 12χ(4)+4χ(8)]|L(1,χ)|4- Ο(p) 和 类似地,当s=0,1,4时,可得 和 而当s=2,5时,可得 定理1证毕。 本文主要研究了半区间上 D.H.Lehmer问题余项E(a,p)在不完整区间上的一种均值分布性质。利用E(a,p)与Dirichlet L-函数的关系以及Dirichlet L-函数的一些均值性质,得到对于不同的参数s,半区间上D.H.Lehmer问题余项的这种双参数均值的主项各不相同,但均不为0,再结合文献[4]中的结论可以看出,这两种区间上D.H.Lehmer问题余项的相消性有显著的差异。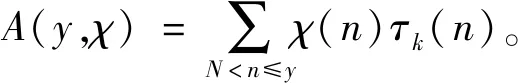
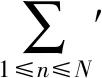
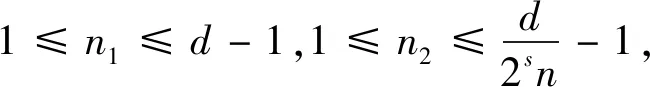
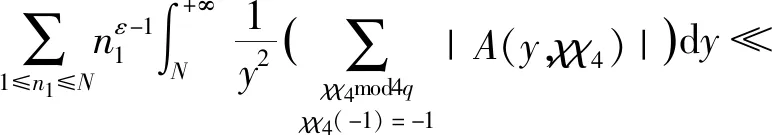
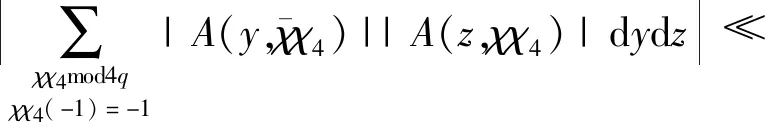
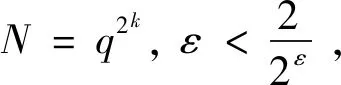
2 定理1的证明
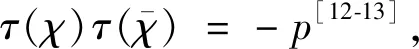
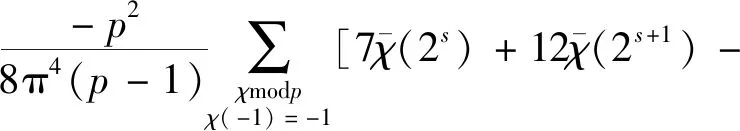
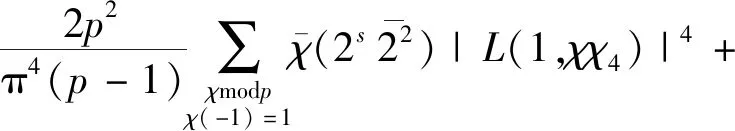
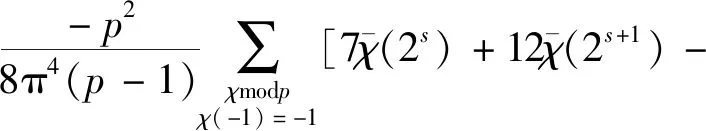
3 结语
