基于正多胞体空间扩展滤波的时变参数系统辨识方法
2020-07-15王子赟刘子幸纪志成
王子赟,张 帅,王 艳,刘子幸,纪志成
(1.江南大学物联网应用技术教育部工程研究中心,江苏无锡 214122;2.江南大学轻工过程先进控制教育部重点实验室,江苏无锡 214122)
1 引言
系统辨识是控制领域学者们持续关注的一个热点问题[1-3].随着科技的发展和系统应用领域的延伸,系统的复杂性越来越高,导致噪声的不确定性已无法采用传统辨识方法中对噪声的既有概率假设进行描述,其本质在于实际系统中的噪声往往是不可测量的,无法直接用假定的概率分布函数来准确表述,诸如最小二乘法[4]、极大似然法[5]等经典算法应用在实际系统中,往往会出现无法辨识或辨识效果不佳等现象.更广泛的情况是,系统的噪声满足有界性,仅能从集合与空间图形的角度分析噪声对系统带来的影响,噪声的概率分布情况未知[6].
集员辨识方法假定参数模型和附加有界误差,进而计算参数的可行解集,确保获得的测量集和所考虑的系统不确定性兼容.在研究系统建模问题时,系统参数的可行解集可以被视为一个多面体,其中多面体的顶点可以由模型结构、测量值和有界噪声准确求解,多面体可由其顶点表述[7-9].同时,在多面体方法的基础上也可以用多面体锥方法描述参数可行解集[10].因为在多面体中所有参数都可以使得系统正常运行,因此这类方法也被称为参数可行解集的精确描述法.然而,虽然精确描述方法可以准确表述参数可行解集,但是其计算量过大,在计算过程中,多面体顶点未知且顶点个数会无规律增加或减少,在计算多面体顶点时,也会随着参数维数的增加而变得相当复杂.为了减少计算负担,需要用近似参数可行解集包裹参数可行解集,其中近似参数可行解集的集合有椭球[11-13]、全对称多胞体[14-16]和正多胞体[17-18]等,这类方法也被称为近似描述方法.相比于精确描述,近似描述计算很简单,却也带来参数可行解集宽松的缺点.在近似描述中,椭球空间描述法因其与卡尔曼滤波的相似性且具有良好性能,近年来受到学者们的广泛关注[19].然而,椭球空间描述法一直存在精度不高、保守性强的缺陷.相比而言,采用正多胞体进行可行集描述,迭代过程计算简单且图形规则.虽然在集员辨识框架中,辨识时不变系统参数的方法和理论已日趋成熟,但跟踪有界误差设置中的时变参数问题仍存在很多不足,例如全对称多胞体法中无法确保包裹k时刻相交区域的全对称多胞体为最小全对称多胞体[20],正多胞体法中扩展系数选择参数变化最大值,无法达到扩展系数选取最优化[21],文献[22]中更新步骤繁琐和文献[23]中H矩阵维数增加使得计算量增加,所以辨识时变参数主要问题在于如何扩展参数可行解集和降低计算量,确保在每一步的变化过程中参数可行解集包含变化后的全部可行参数解.与时不变参数集员辨识过程相似,但此类递归算法仍然没有最优扩展参数可行解集.
本文提出一种基于正多胞体空间扩展滤波的有界时变参数辨识方法.相比于可行解集对应的其他空间结构类型,正多胞体的形状更加规则,且各边都垂直或平行于坐标轴,可以清晰展示在跟踪参数变化时参数可行集的移动状况.相比于文献[24],本文优化了扩展系数的选取,不是通过求取参数变化的最大值简单确定扩展系数,而是通过构造扩展系数方程,求解前k步扩展系数最优解得到,同时在辨识过程中,动态更新正多胞体约束条件.相比于文献[25],本文提出的方法在求解正多胞体时仅需要求解少量参数的线性规划问题,在扩展系数确定后,再确定每一步正多胞体约束条件,使得扩展后的正多胞体包含变化后的参数,减少了计算多面体顶点的繁琐步骤,从而降低了运行过程的计算量.
2 问题描述
线性参数模型可以写成以下回归向量形式:
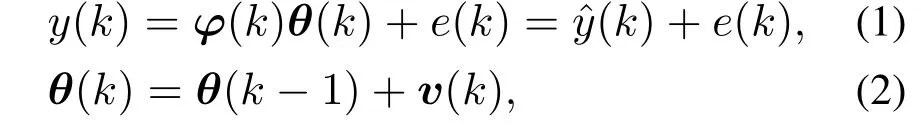
在本文中,满足模型(1)的全部可行参数采用正多胞体空间结构包裹,其约束条件可表示为

其中:A0∈Rn×nθ,b0∈Rn.式(2)定义了时变参数θ的变化上界取决于γ.按照γ的取值,系统(1)存在3种分类情况:
1) 时不变参数情况,γ=0;
2) 有界时变参数情况,0 <γ <∞;
3) 无界时变参数情况,γ=∞.
在本文中,主要研究有界时变参数系统中的参数辨识问题,即0 <γ <∞.通过在时不变参数系统约束条件下构造扩展系数方程,将参数可行解集在扩展之后包含参数变化的最优解γ作为最终扩展系数,而不是简单地选取θ变化的最大值作为扩展系数,从而优化了扩展系数的选取过程,解决了当前正多胞体辨识时变参数保守性高和多面体辨识时变参数计算复杂度高的缺陷.
3 正多胞体空间描述
定义1描述近似参数可行集的正多胞体O:

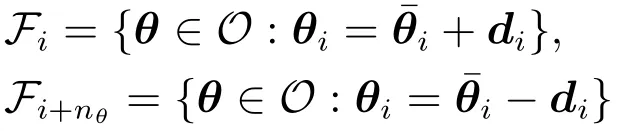
为正多胞体O的一对结构面.
可以看出,正多胞体由约束条件Θ决定,通过求解2nθ个线性规划方程可以得到包裹参数可行解集的最小正多胞体O*(Θ).


其中:Θ(k)为2nθ个约束条件可行解集的交集;ei表示nθ维单位矩阵的第i列,i=1,2,…,nθ.通过求解线性规划方程可以得到第k步每个参数的上下界,从而得到最紧致正多胞体其中:

4 基于正多胞体空间扩展滤波的时变参数辨识方法
若γ=0,即系统处于时不变状态,有θ(k)=θ,此时系统的不确定性仅表现在未知但有界的噪声.因此,对于每一时刻k,由测量值和回归向量φ(k)得到包含参数空间的一个超平面带Fk,
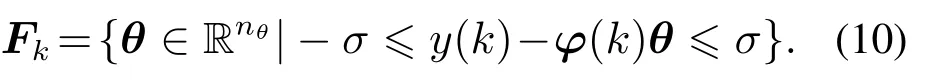
第k步正多胞体由前k-1时刻超平面带和初始正多胞体相交得到

其中:Θk为第k步多面体为第k步包裹多面体的正多胞体.与求解时不变系统参数不同的是,在求解时变参数时,需要改变约束条件来扩大正多胞体,否则正多胞体无法包含参数变化状态下的可行解,导致辨识错误或者误报为空集.本文通过扩展系数扩展约束条件,进而放大扩展正多胞体,最终达到扩展参数可行解集的目的,扩展后的正多胞体和多面体分别表示为记前k-1步扩展,第k步不扩展正多胞体和多面体分别为
定义2Fi|k(i≤k)是第k时刻在第i时刻的基础上扩展超平面带,

其中Δi|k是由于从时刻i到k的参数变化引起的输出估计的偏差界限,且有

在系统参数时变状态下,考虑到参数变化上界γ,有

注1由式(10)和式(12),可以得到Fk|k=Fk,即参数可行解集相同.
第k步非扩展的正多胞体由前k-1时刻扩展超平面带和初始正多胞体相交得到
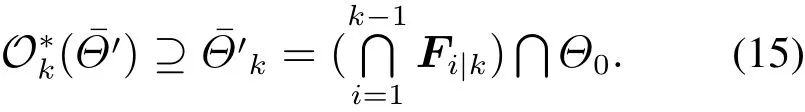
推论1假设k总是辨识的最后一步,已知

分别是在Rn上的多面体和正多胞体,那么C(k)⊕v(k)无意义,则k时刻参数可行集C(k)满足

其中:

证假设有θ∈C(k-1)⊕v(k-1),将存在α∈C(k-1)和‖βi‖1≤‖vi(k-1)‖1,其中βi,vi(k-1)分别表示β,v(k-1)的第i个元素,所以θ=α+β,从而得知

当i=k时,θ只需满足第k步超平面带,无需扩展;当i <k时,|AAA|<(k-i)‖φ(i)‖1,其中|AAA|表示矩阵AAA的行范数,φ(i)表示A的第i行向量,矩阵A和b随步数增加自动更新,得到式(17).所以可以得到θ∈¯C.而且因为α∈C,那么一定存在α∈ooo*(C),因此

证毕.
当γ=0时,第k步正多胞体约束条件表示为
2018年6月15日,在河南省郑州市郑东新区,位于七里河南路与康平路交叉口的宏光意中大厦配楼同文酒店的门前人潮涌动。所有的来宾都满怀期待地迈向二楼,在两侧摆满祝贺花篮的大厅正中是一面墙,墙上呈现河南著名书法家王澄所题的“国学博览馆”五个行楷大字。这一天是宏光集团公司历时5年,由王澄呕心沥血、殚精竭虑担纲策划,开创国学博览馆开馆揭幕的大喜之日。

依据推论1中式(17)和定义2中式(14),当i=k时,Δi|k=0,当γ >0时,第k时刻非扩展正多胞体约束条件:是从1到k-1时刻扩展情况下Ak的行数.

第k时刻扩展正多胞体约束条件为

其中:

ak;i是矩阵Ak的第i行,Δbk-1;i是Δbk-1的第i个值.此时,式(24)可以看作一个关于γ的线性规划方程,其余参数可由系统测量值和初始定义正多胞体获得,因此γ满足线性规划方程:

其中:f=(0,…,0,1),x=(θTγ)T,长度为nθ+1.当前k时刻所有γk得到后,最终的扩展系数

图1描述了相同情况下扩展正多胞体和非扩展正多胞体的变化趋势,虚线包裹区域代表扩展正多胞体,实线包裹区域代表无扩展正多胞体,黑线包裹区域代表初始正多胞体,因为在扩展多胞体情况下,约束超平面带变宽,可以看出扩展正多胞体尺寸更大,以便包含时变参数.
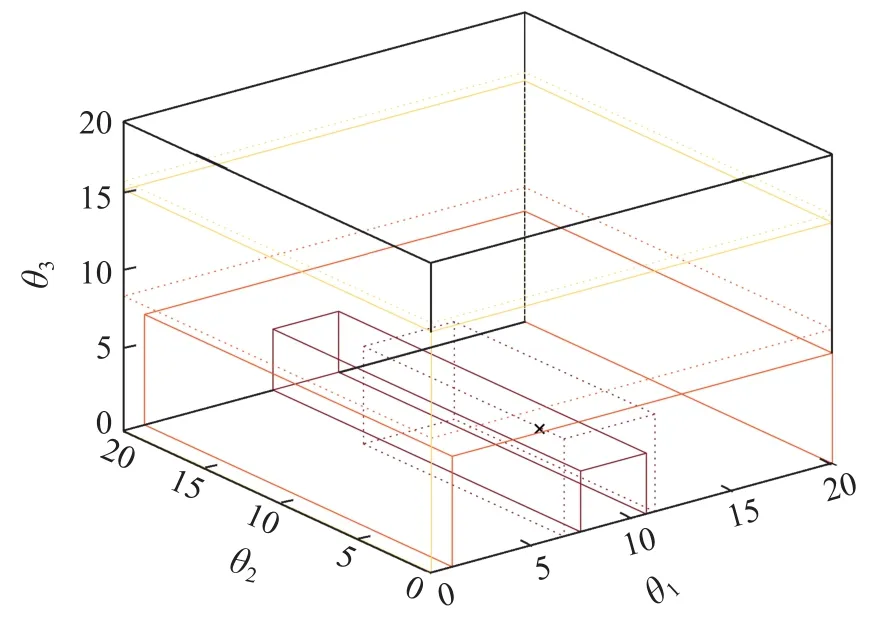
图1 正多胞体空间扩展变化情况Fig.1 The space variation of the extended orthotope
基于正多胞体空间扩展滤波的时变参数辨识方法算法步骤:
步骤1定义辨识步数为L,定义初始正多胞体,得到初始约束条件A0θ≤b0,γ0=0;
步骤2根据输入数据u(k),测量数据y(k)和回归向量φ(k)构造第k步非扩展正多胞体约束条件,
步骤4更新γ值,γ=max(γ,γk).当k=L时得到最大扩展系数γ,同时重置k=1,否则设置k=k+1,返回第2步;
步骤5由式(25)更新扩展正多胞体约束条件
步骤6分别取i=1,2,…,nθ,求解正多胞体顶点,
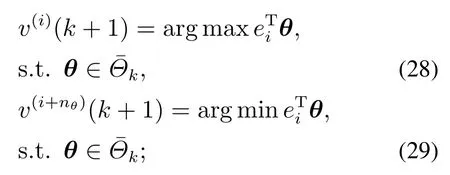
步骤7构造扩展正多胞体

其中:

步骤8置k=k+1,返回第5步;当k=L时,算法结束.
5 仿真分析
例1考虑下列线性参数模型:
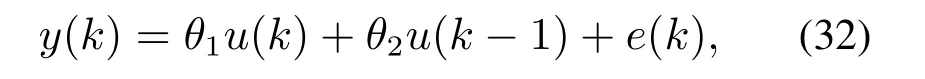
其中:θ1,θ2为待辨识的时变参数,其真实的变化情况分别为

e(t)为未知但有界噪声,取输入信号u(t)∈U[-5,5],系统噪声e(t)∈U[-0.3,0.3].为比较跟踪参数变化的情况,定义欧氏距离Δθ=其中θ为参数变化时的真实值,ˆθ为时变参数估计值[26].
采用本文方法辨识参数变化值时效果如图2-3所示.
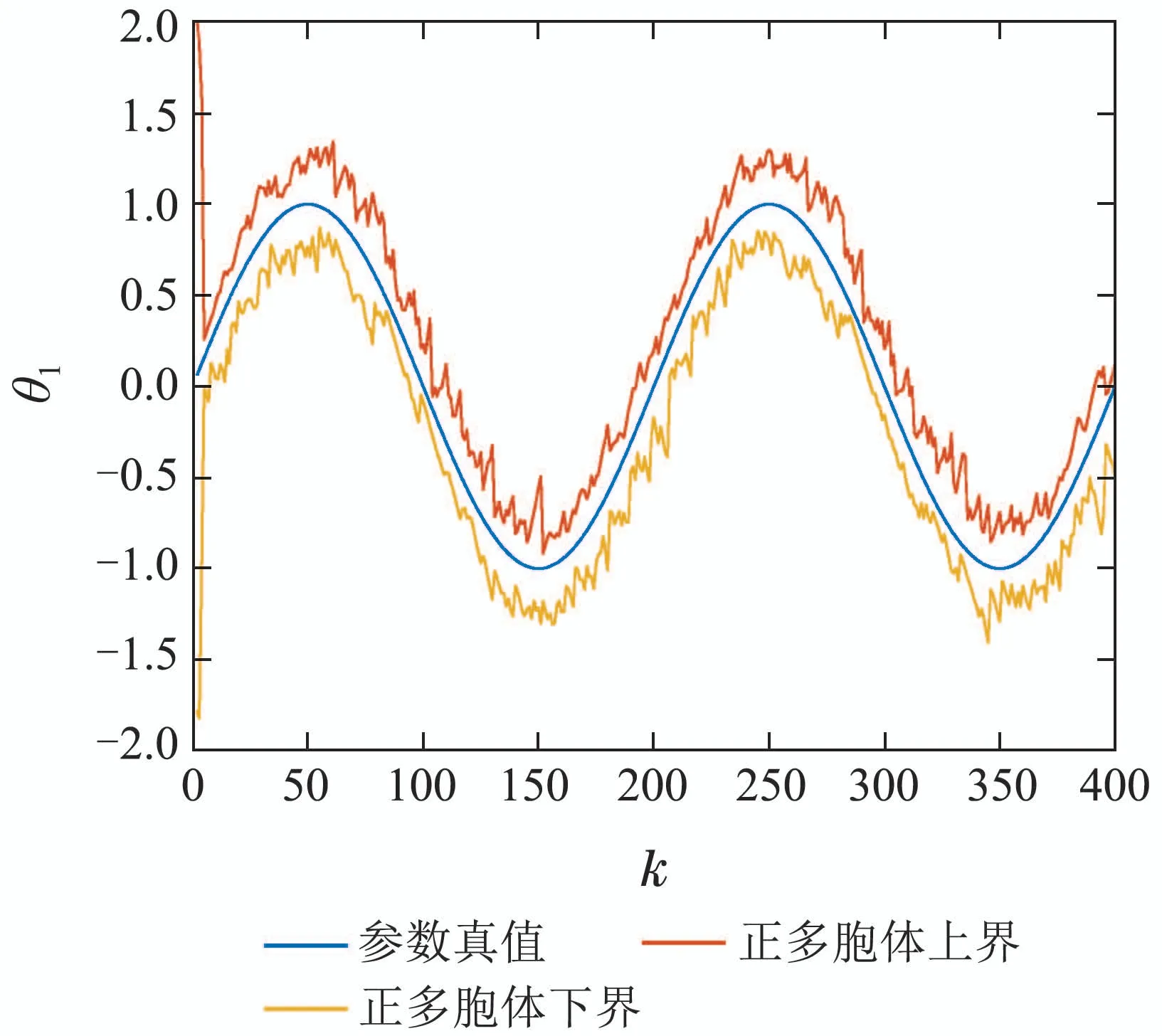
图2 参数θ1辨识曲线Fig.2 Identification curve of parameter estimate θ1
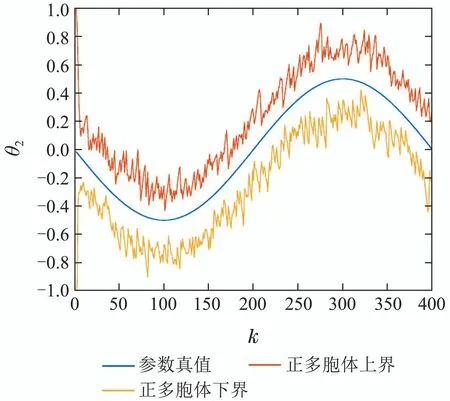
图3 参数θ2辨识曲线Fig.3 Identification curve of parameter estimate θ2
从图2-3可以看出,基于正多胞体空间扩展滤波的有界时变参数算法能够有效辨识时变参数,参数真值一直位于正多胞体上下界范围内,随着参数变化,正多胞体估计值跟踪变化,具有很好的效果.
接下来设置参数θ1不变,参数θ2=-0.5×sin(π×k×0.01),与文献[24]中选择参数变化最大值作为扩展系数方法和文献[25]中多面体方法比较的仿真结果如图4-5所示.
从图4-5均可看出,正多胞体方法和多面体方法可行参数解集上下界相同,最大值正多胞体上下界要明显大于其余两种方法,且正多胞体的中心值相较多面体的中心值和参数变化最大值方法更加贴近真实参数点.与两种方法比较的对比分析仿真结果分别如图6-7所示.
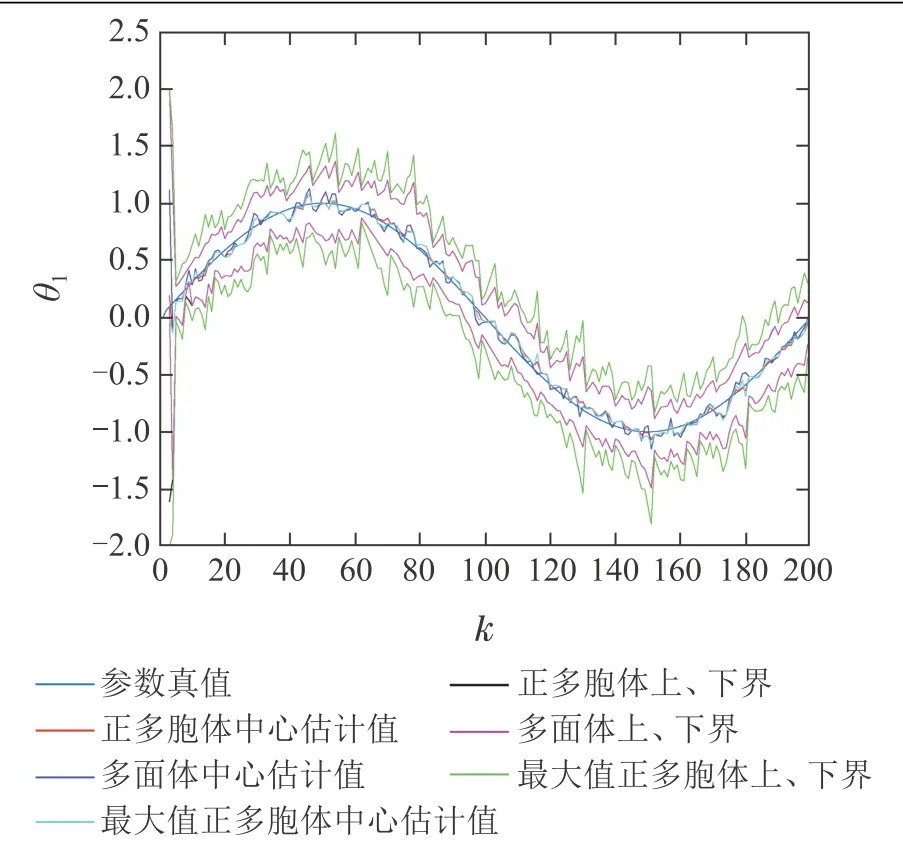
图4 正多胞体和多面体辨识时变参数θ1比较情况Fig.4 Comparison of time-varying parameter estimate θ1 between orthotopic and polyhedral based algorithms

图5 正多胞体和多面体辨识时变参数θ2比较情况Fig.5 Comparison of time-varying parameter estimate θ2 between orthotopic and polyhedral based algorithms
图6中,本文在k=50~140范围内间隔15步取正多胞体和多面体数据,记号“x”表示当前时刻参数真值,记号“o”表示当前时刻正多胞体中心估计值,记号“*”表示当前时刻多面体中心估计值,记号□表示最大值正多胞体中心估计值.图6中,不同颜色下标准矩形包裹区域实线表示正多胞体,点划线表示最大值正多胞体,矩形内图形包裹区域表示多面体.可以看出正多胞体中每个参数的最大和最小值是根据准确描述可行参数解集的边界上下限确定,所以基于正多胞体空间扩展滤波方法和基于多面体的空间扩展滤波方法在辨识时变参数时上下界一致.就辨识精度而言,图6中的正多胞体中心估计值更接近参数真值,反映出基于正多胞体空间扩展滤波方法针对时变参数变化可以做到更有效的跟踪.从图7中可以看出,在以欧式距离为依据判断算法优劣的过程中,考虑到时变参数系统中参数每一时刻都在变化,估计值也会随着参数变化而时刻跳动,所以在误差分析曲线中,误差曲线并不是逐渐减小最终趋于不变,但是在误差分析过程中,基于正多胞体空间扩展滤波方法的估计误差要比基于多面体空间扩展滤波方法更小.

图6 正多胞体和多面体辨识过程中递归演化Fig.6 Recursive evolution by the orthotopic and polyhedral algorithms

图7 正多胞体和多面体误差曲线对比Fig.7 Comparison of error curves by the orthotopic and polyhedral algorithms
例2为了进一步验证基于正多胞体空间扩展滤波方法解决有界时变参数系统辨识问题的有效性,下面采用风力发电机浆距子系统作为仿真示例进行分析.
在风力发电机系统中,浆距子系统是控制桨叶和浆距角的重要组成部分,如图8所示.其结构模型为[27]
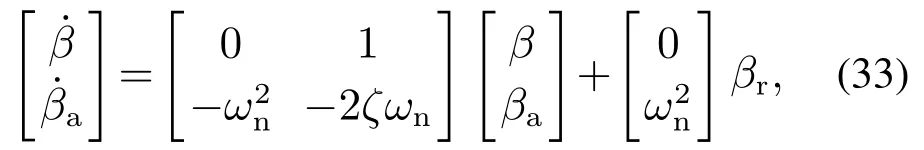
其中:β和βa分别为浆距角和角速度大小,βr为浆距参考值,ζ和ωn分别为阻尼系数和系统自然频率,ζ和ωn会随着液压的变化而变化,主要是由于主线压力下降,液压系统中所考虑的故障可能导致参数动态变化.这种动态变化是标称值0.6 rad/s和0.9 rad/s之间的阻尼系数的变化以及3.42 rad/s和标称值11.11 rad/s之间的系统自然频率的变化[28].将桨距子系统数学模型(33)近似为二阶系统[29]

其中:y=β,u=βr.为了满足参数在规定区间内动态变化,将阻尼系数和自然频率的变化分别设置为

据文献[27]取采样时间为Ts=0.01 s,对该闭环系统离散化为A(z)y(t)=B(z)u(t)+e(t).根据离散化条件,A(z),B(z)均为多项式,其中:
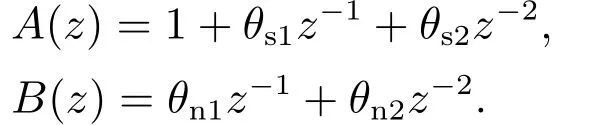
为了验证所提算法跟踪参数变化的有效性,在参数变化过程中,分析B(z)多项式对应的待辨识参数并描述参数辨识效果和正多胞体演化情况,并取输入u(t)∈U[-25,25],噪声e(t)∈U[-0.01,0.01].同时与文献[24]中选择参数变化最大值作为扩展系数进行对比,比较结果如图9-10所示.

图8 风力发电机系统Fig.8 Wind turbine system
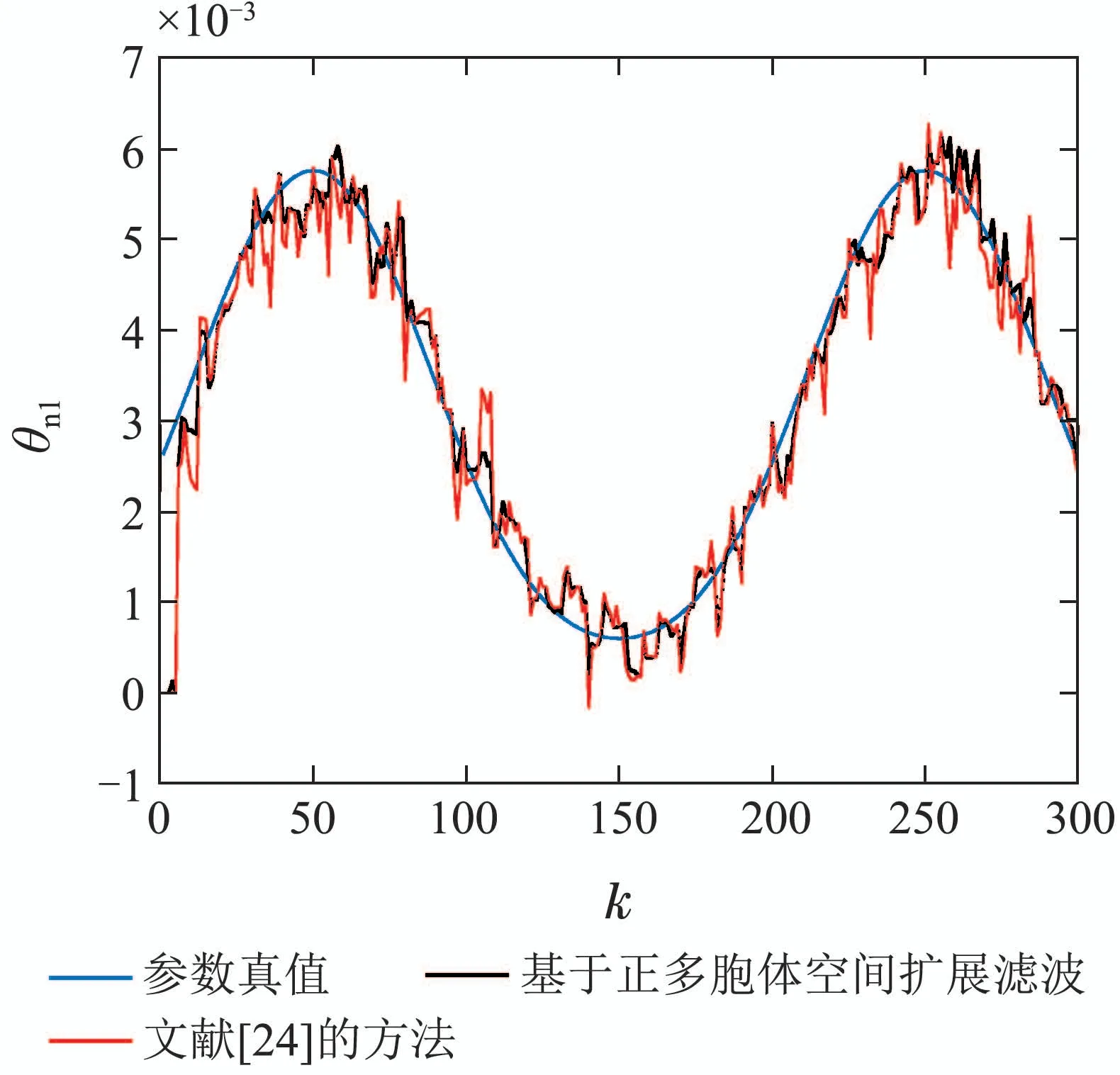
图9 扩展系数不同时参数估计θn1比较Fig.9 Comparison of parameter estimates θn1 when the expansion coefficients are different

图10 扩展系数不同时参数估计θn2比较Fig.10 Comparison of parameter estimates θn2 when the expansion coefficients are different
从图9-10中可以看出,采用本文方法和文献[24]提出的方法分别求解扩展系数,都能有效地跟踪时变参数变化情况.相比而言,本文提出的基于正多胞体空间扩展的滤波方法辨识过程更平滑,受噪声扰动的影响更小,优于文献[24]提出的选择参数变化最大值作为扩展系数方法.
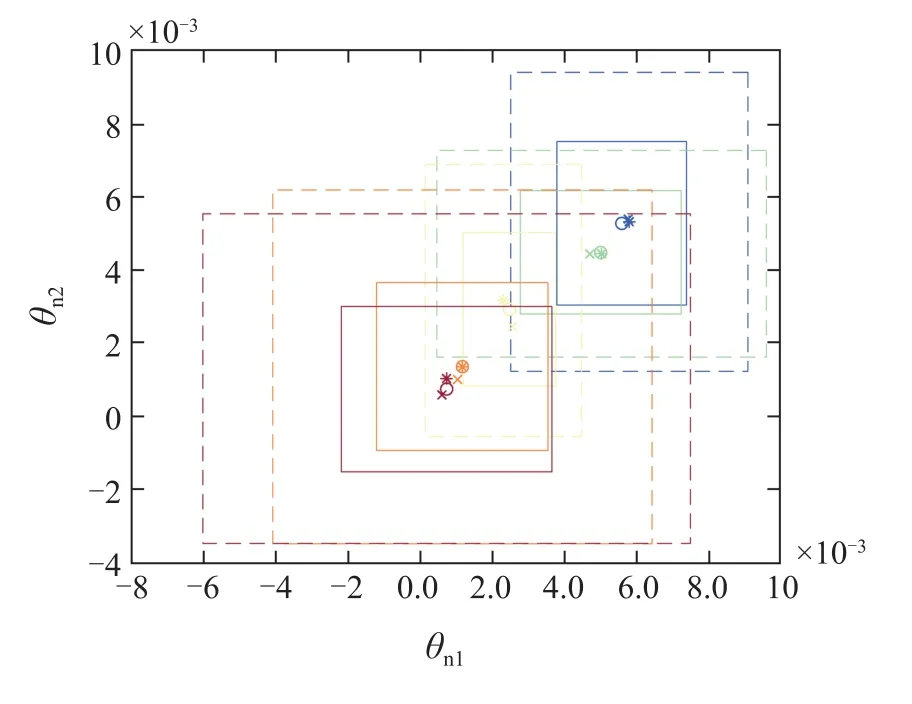
图11 扩展系数不同下的正多胞体递归演化Fig.11 Recursive evolution of orthotopes with different expansion coefficients
此外,图11中在k=50~150之间间隔25步取不同扩展系数正多胞体数据,记号“x”表示当前时刻参数真值,实线包裹区域和记号“o”分别表示当前时刻线性规划扩展系数正多胞体和正多胞体中心估计值,虚线包裹区域和记号“*”表示当前时刻选择参数变化最大值扩展系数正多胞体和正多胞体中心估计值.可以看出基于线性规划的正多胞体要更紧致,因此算法保守性更低,中心估计值也更靠近参数真值.
6 结论
本文基于正多胞体滤波过程,结合线性规划求解参数扩展系数,提出了一种时变线性系统参数辨识算法,在给定的噪声和参数变化上下界的条件下,仅依据测量值和系统观测值求得扩展系数最优解.本文所提出的正多胞体空间扩展滤波方法在辨识时变参数过程中,利用正多胞体的空间扩展和移动描述了辨识过程,同时在计算过程中,通过求解有限个线性规划问题得到紧致的正多胞体,计算步骤简单.此外,本文通过数值仿真和风力发电机的浆距子系统为例分别进行仿真,可以直观看出该方法辨识有界时变参数的可行性和有效性.
