关于一类poly-Dedekind DC和的研究

马元魁,罗玲玲,KIM Taekyun,2,李红泽

(1.西安工业大学 基础学院,陕西 西安 710021;2.光云大学 数学系,韩国 首尔 139-701;3.上海交通大学 数学科学学院,上海 200240)

关于Dedekind和以及各种类似和式的研究在解析数论、模形式、特殊函数理论、代数数论、组合几何、拓扑学以及算法复杂性研究中占有举足轻重的位置,并和Dedekind函数的转化公式、类数、格点问题、DirichletL-函数的特殊值问题、群在流形上的作用以及随机数生成器等问题密切相关。

Apostol研究了推广的Dedekind和,把Dedekind和中第一类Bernoulli函数替换成任意Bernoulli函数,并得到了一个互反公式[1-2]。

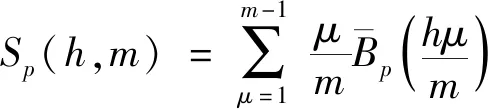
(1)

式中,[x]表示不超过x的最大整数。

作为Apostol广义Dedekind和的推广,Kim 等研究了用第二类poly-Bernoulli 函数定义的poly-Dedekind和[3]。 Ma Y K等研究了用poly-

Bernoulli 函数定义的poly-Dedekind和[4]。

(2)

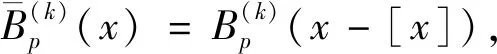
Kim研究了Dedekind DC和[5]

(h,m∈N)

(3)

Ma Y K等研究了poly-Dedekind DC和,把Dedekind DC 和中Euler函数替换成用polyexpo-

nential函数定义的poly-Euler函数[8]。

(4)

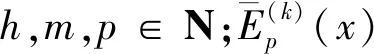
Simsek研究了Dedekind DC 和的三角函数表示,并得到了它与其它一些函数或者和式的关系[6],如Clausen函数、polylogarithm函数、Hurwitzζ函数、Hardy-Berndt 和等。此外,Bayad和Simsek研究了推广的Apostol-Dedekind-Rademacher和,推广了经典的Dedekind-Rademacher和,可以用Jacobi模形式、余切函数或Barnes多重zeta函数的特殊值表示[9]。他们证明了这些和式满足互反关系,并能从中推导出一些著名的互反关系。本文的目的是探索与模形式、ζ函数以及三角和等有关的新的形式的和。

本文进一步推广了Dedekind DC 和,研究了 poly-Dedekind DC 和,用polylogarithm函数定义poly-Euler函数,并证明它满足互反关系。

(5)

式中:m,h,p∈N;m≡1(mod 2);h≡1(mod 2);k∈Z。

当k=1时,此互反公式退化成Dedekind DC和的互反公式(见推论 2)。

mpTp(h,m)+hpTp(m,h)=2(mh)p-1×

式中:m,h,p∈N;m≡1(mod 2);h≡1(mod 2)。

1 预备知识

首先回顾一些符号和定义。已知Euler多项式定义如下[1-19]

(6)

式中,En=En(0)称为Euler数。

由式(6)可以得到[1-19]

(7)

由式(6)还可以得到En(1)+En=2δ0,n,(n≥0),δn,k表示Kronecker符号。

由式(6)可以推出

(n∈N)

(8)

已知polylogarithm函数定义为[10-11]

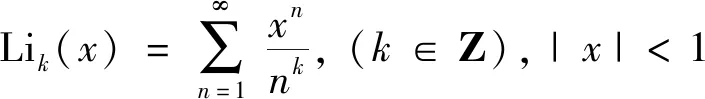
(9)

当k=1时,Li1(x)=-log(1-x)。

设n是非负整数,第二类Stirling数定义为[10,12]

(10)

2 由poly-Euler 函数定义的poly-Dedekind DC 和

对每一个整数k,定义poly-Euler多项式如下

(11)

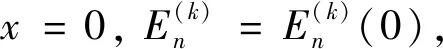
(12)

把Dedekind DC和中Euler函数替换成用polylogarithm函数定义的poly-Euler函数,定义poly-Dedekind DC和为

(13)

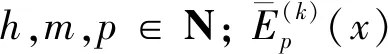
由式(11) 有

(14)

因此,可得

(15)

另一方面,

(16)

因此,由式(15) 和式(16)可得如下定理。

定理1对于任意n∈N,有

令k=1,由定理1可得如下推论。

推论1对于任意n∈N,有

式中δn,k表示Kronecker符号。

接下来的引理同文献[8]中的引理1、引理2、定理7及定理8。

引理1对于p,s∈N且s

引理2对于p∈N,有

引理3对于m∈N且m≡1 (mod 2),p≡1 (mod 2)且p>1,有

引理4对于h,m,p∈N且(h,m)=1,m≡1 (mod 2),有

对于d∈N且d≡1 (mod 2),有

(17)

因此,由式(17) 可以得到如下定理。

定理2对于k∈Z,d∈N且d≡1 (mod 2),n≥0,有

S2(n-j+1,l)。

对于m,h∈N且m≡1(mod 2),h≡1(mod 2),由式(13)和定理2,有

(-1)p-j+1+v+l2p-j+

(-1)p-j+1+μ+l2p-j=

(-1)p-j+1+v+l2p-j+

(-1)p-j+1+μ+l2p-j=

(-1)p-j+1+l2p-j(-1)μ+v×

(18)

因此,由式(18)可以得到poly-Dedekind DC和的互反公式如下。

定理3对于m,h,p∈N,k∈Z且m≡

1 (mod 2),h≡1 (mod 2),有

(-1)p-j+1+l2p-j(-1)μ+v×

当k=1,由推论1可知,以上定理可以退化成Dedekind DC和的互反公式。

推论2对于m,h,p∈N且m≡1 (mod 2),h≡1 (mod 2),有

mpTp(h,m)+hpTp(m,h)=

3 结语

Dedekind和及其推广是由Bernoulli函数及其推广定义的,Dedekind DC 和及其推广是由Euler函数及其推广定义的,而且它们都满足互反关系。作为Dedekind DC和的进一步推广,本文研究了 poly-Dedekind DC和,由polylogarithm函数定义了 poly-Euler函数,并证明了它满足互反关系。