复杂开曲面的鲁棒布尔运算
2020-03-19刘凯正刘利刚
刘凯正, 刘利刚
(中国科学技术大学数学学院,安徽 合肥 230026)
在计算几何、计算机辅助设计及计算机图形学等领域中,布尔运算是一种构造实体的常用方法。网格的布尔运算在19世纪80年代被提出,后续的研究主要集中在提升算法的效率与准确性方面。而本文提出的布尔运算算法,在兼顾效率与精度的同时,拓宽了布尔运算的适用范围。
在布尔运算发展的早期,由于二叉空间分割(binary space partition,BSP)树内在的空间划分性质,有很多基于 BSP树的算法被提出。但这类算法有2个明显的缺点:一是有很多无必要的分割,如图1所示,当图1(a)的多边形转为BSP树时,边d被分为d1和d2,若未有其他边与边d相交,就没有必要做分割;二是不能对多个模型同时进行运算。基于 BSP树的布尔运算算法一般是先将其中一个模型转为BSP树,再将另一个模型转为BSP树并将其转为多边形结构,然后插入最初的 BSP树中,并根据布尔运算的类型提取多边形。所以该类布尔运算一次只能对2个模型进行运算,如果有多个输入,将会导致严重的性能问题。由于这2个问题均源于 BSP树本身,难于做改进,所以现在已鲜有人基于BSP树来研究布尔运算。

图1 将多边形转为BSP树
网格布尔运算是求交运算,所以最近很多算法都未借助复杂的数据结构,而是直接求出网格的相交元素。其难点在于正确归类揉合所有输入网格所划分的空间区域。所以现有的大量布尔运算算法对输入有严格要求,如不能有空洞、不能是非流形、不能有退化的三角形及不能有自交等。近些年随着布尔运算的发展及完善,这些限制条件已逐步被移除。但现有的大多数算法均要求输入是能作为实体模型边界表示的封闭网格,而在实际应用中,输入的大多为有边界边的开网格,并希望能对其进行运算。如图2所示,2个开圆环面A和B按图2(c)摆放,并进行布尔并运算,希望能得到如图2(d)所示的封闭圆环面。为此本文提出了一种能适用于开网格的布尔运算算法。
基于 BSP树的算法对于网格每一个面片都是根据其法向分出内外,这种只做局部考虑的特性允许输入是开网格。但正是因为没有从整体上考虑网格所划分的空间区域,所以会得到与期望不符的结果。如图3所示,输入2个抛物面,对其分别进行布尔交与布尔并运算,基于 BSP树的布尔运算不仅不能保证输出的是封闭网格(图 3(d)),而且从图3(c)和(d)可以看出不符合A∩B⊆A∪B的逻辑。而本文算法则不会引起类似的错误。

图2 2个非封闭圆环面做并运算

图3 本文算法与基于BSP树算法的比较
布尔运算中有大量的求交计算,普通的浮点运算极易导致数值上的错误,从而可能引起输出网格顶点位置错误及拓扑混乱等一系列问题。为此,很多关于布尔运算的文献用大量篇幅去阐述如何避免数值错误的方法。但实际上,求交运算只需要用到加减乘除4种运算,且于有理数域上封闭。此外,常见的保存网格的OBJ文件及OFF文件均用3个有限位的小数去表示顶点在R3中的位置,所以其属于Q3。CGAL的几何库实现了一种运算核EPECK,且能在有理数域上进行无损计算(如果所有参与的运算在有理数域上封闭,如加减乘除满足条件,而sin及sqrt等则不满足)。而本文算法的实现正是采用了此运算核,因此不会引起任何数值上的问题。
1 相关工作
自文献[1-3]提出关于网格的布尔运算后,有大量工作对其进行了完善及发展。如文献[4]提出基于GPU栅格化的多边形布尔运算,该方法能快速计算,但在进行栅格化时会有精度丢失。文献[5-6]提出了基于 BSP树的布尔运算,后续有很多研究者对此做了大量完善及扩充。文献[7]基于BSP树,用平面作为整个算法构建的基本元素,将点用3个平面相交来表示,这样不用显式求出交点,从而避免了浮点运算可能引起的错误。而文献[8]在文献[7]的基础上,提出用八叉树将空间分成多个区域;然后只在有相交产生的区域局部建立BSP树,较文献[7]算法的效率有显著提高。但基于 BSP的算法均有一个明显的缺点:在建 BSP树时会将多边形转为平面,而平面的无界特性会使得在划分空间区域的过程中做多余的分割,过度加细。
CGAL库是一个众所周知的开源几何库[9],其布尔运算在鲁棒性方面仍然代表最高水准。并实现了一种运算核:EPECK,通过该运算核,能在有理数域上做无损计算。为了保证算法的鲁棒性,本文采用了该运算核。但 CGAL中的布尔运算需要将输入转为Nef多边形[10-11],这是一种复杂的数据结构,运行时会占用大量内存,在效率方面也不尽人意。此外,对输入也有苛刻的要求,例如不能有空洞,只能具有一个连通分支等。所以 CGAL库中的布尔运算虽然具有最高水平的精度,但性能表现不佳。
文献[12]提出将网格沿着交线分成不同的流形块,最后输出的网格是流形块拼装的结果。而文献[13]在文献[12]的基础上提出胞体的概念,并通过计算胞体的环绕数来判定胞体相对于输入网格的内外关系。文献[13]中的算法已集成在 libigl库中[14],但其只适用于封闭网格,无法计算开网格所形成的胞体的环绕数。本文通过添加虚拟流形块用于封闭胞体,进而正确判断内外关系。该算法适用于更多类型的网格,网格可以是封闭也可以是非封闭的,可以有多个连通分支,可以有空洞。而布尔运算是一种构造实体的方法,所以本文算法可以保证最后输出的一定是实体或者空集。
2 流形及环绕数
首先介绍一些有关拓扑流形网格的概念[15]。对于网格的任意顶点v,可用N(v)表示网格中共享顶点v的所有三角形形成的邻域。如果N(v)中所有三角形按序排列且使得序列中所有 2个相邻三角形都共享一条以顶点v为端点的边,则将顶点v叫做流形顶点。如果网格中的一条边e恰好被2个三角形共享或者只属于某个单个三角形,则将边e叫做流形边。如果边e只属于一个三角形,将边e叫做边界边。如果网格中所有的顶点和各边都是流形的,则网格也是流形的。
对于任意一个网格,若其中一个子网格恰好为一个流形,则可将其称为流形块(patch)[13],将流形块围成的封闭区域叫胞体(cell)。
为了便于观看和阐述,图 4给出了二维的情形,读者可类比到三维情形。图4(a)中不同颜色的曲线段表示流形块,图4(b)中不同颜色的区域表示胞体。

图4 流形块和胞体
对于二维空间,定义点p关于闭的利普希茨曲线C的环绕数(winding number)为当沿逆时针走完曲线C时绕点p的圈数[16]。不失一般性,可令点p=0。此时环绕数w(p)为

如图5所示,点P0的环绕数为-1,点P1的环绕数为1,而点P2环绕数为0。

图5 环绕数
同样地,如果点p∈R3,S为闭的利普希茨曲面,则令点p关于S的环绕数为

点p关于S的环绕数是一种有符号的整数,反映了S包围点p的层数。从离散的观点看,如果M={fi}为封闭网格,其中fi为三角形;令Ωi(p)为三角形fi关于点p的有向空间角度[16],则

如果三角形f的3个定点分别为:v0,v1,v2,令a=v0-p,b=v1-p,c=v2-p,a=||a||,b=||b||,c=||c||,则[16]
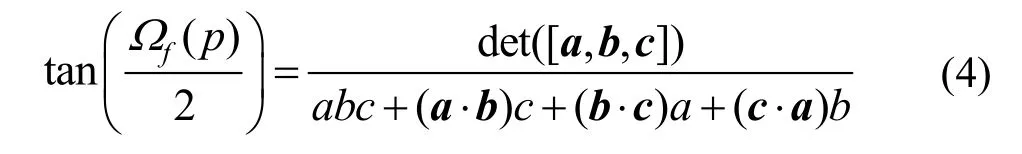
其后的布尔运算算法会用一种巧妙的方式求胞体的环绕数,不会用到复杂的式(4)。
3 本文算法
对于输入的n个网格 {Mi}i∈{1,…,n}(为方便阐述,令n=2,即输入为A和B2个网格,为更具一般性,以开网格为例,如图 6所示),须满足如下条件:在经过步骤1解决自交问题后,检测每条非流形边ab,令count表示与ab相关的一个整数,初始时为0。然后找到所有共享ab边的三角形,若ab边在此三角形中的顺序恰好为“ab”,则count加 1,若顺序为“ba”,则count减 1。若所有非流形边所对应的count均为0,则是有效输入。
本文算法流程如下:
输入:网格A和B。
输出:布尔运算得到的网格。
步骤1.合并A和B,并解决自交问题;
步骤2.划分流形块并删除含边界的流形块;
步骤3.标记胞体;
步骤4.建立虚拟流形块;
步骤5.计算胞体的环绕数;
步骤6.根据环绕数输出网格。
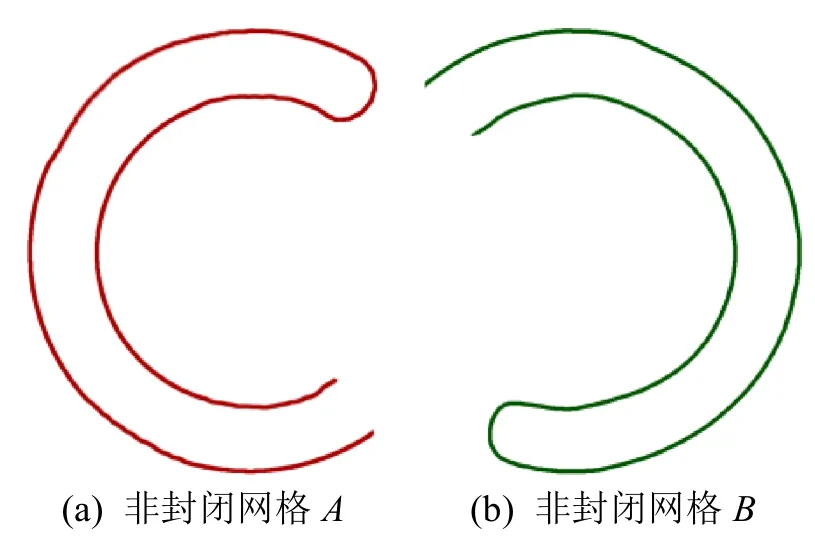
图6 输入网格
对于任意网格M,可用V(M)={v1,v2,···,vr}表示M的r个顶点,用F(M)={f1,f2,···,fs}表示M的s个面。
3.1 标记流形块及胞体
步骤1.将A和B合并到一张网格M0上。此过程只是纯粹地将V(A)和V(B)以及F(A)和F(B)进行集合并操作。此时M0可能会有自交。M0中每个三角形对应一个平面,P为所有平面形成的集合。那么,对于任意平面p∈P,可找出所有与此平面相交的元素,这些元素可能是三角形、线段或点。将所有这些元素作为限制条件,在平面P上进行二维的带约束的 Delaunay三角化(constrained Delaunay triangulation,CDT)。记C(M0)为CDT之后的所有三角形形成的集合。对于三角形f∈C(M0),如果f被F(M0)中某个三角形所包含,则保留,否则舍弃。将所有保留的三角形所形成的网格记作M1。M1与M0相比,V(M0)⊂V(M1),且任意f∈F(M1)一定被某个f′∈F(M0)所包含。所以M1是对M0的加细,M1不包含任何相交的三角对,并且没有丢失或改变M0的任何形状信息。如图7所示。

图7 解决自交问题
步骤 2.为了确认M1中的每个三角形所在的流形块,可采用宽度优先搜索算法,通过遍历每个三角形f∈F(M1),然后检查f的每条边e,如果e为流形边,则将包含e的另一个三角形f′与f归在同一个流形块。如图8所示,用不同颜色来区分流形块。
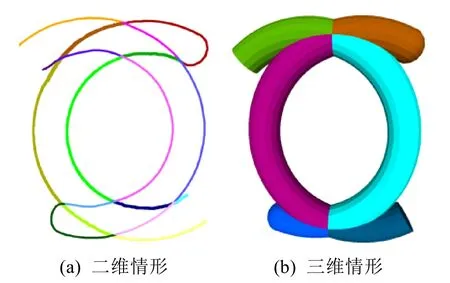
图8 划分流形块
本文算法允许输入是开网格,而开网格并不具有决定一个唯一实体的完备信息。修补开网格的方法,即使其成为一个封闭的网格。采取不同的修补算法可得到不同的被修补的网格,从而影响最终布尔运算的结果。本文算法则是通过所有输入去决定开网格所代表的实体模型。其并不是一成不变的,而是随着输入的变化而变化。如图9所示,一个抛物面与不同的网格做布尔运算,其潜在所表达的实体模型是不同的。至于具体用哪些流形块来修补,则是通过步骤 5建立虚拟流形块来计算胞体环绕数决定的,而这一步仅仅是将包含边界边的流形块舍去,如图10所示。

图9 根据所有输入决定开网格所代表的实体

图10 去掉包含边界边的流形块
步骤3.为了标记胞体,首先遍历网格M2中的每条边,如果这条边为非流形边(共享此条边的三角形个数大于2),此时共享此边的每个三角形必定属于不同的流形块。这样,就可知流形块之间的相邻关系。三角形3个顶点的排列顺序指定了其法向的方向,因为流形块中所有三角形的法向是一致的,所以可将其中任意一个三角形的方向记作此流形块的正方向。每个流形块p与2个胞体相邻,将p正方向对应的胞体记作C+(p),负方向记作C-(p)。以每条非流形边e为轴心,按逆时针方向排列共享该条边的三角形,得到循环序列Sf(e)。而每个三角形fi∈Sf(e)对应一个流形块pi,从而得到一个对应的流形块序列Sp(e)={···,pi,pi+1,···}。对于任意一对相邻的流形块pi,pi+1∈Sp(e),令胞体pi与pi+1等同。如图11(a)箭头所示2个流形块,左边记为p0,右边记为p1,那么按照先前的叙述则应C_(p0)=C_(p1)。如果M2是连通的,则此时所有胞体已被标记。
如果M2有多个连通分支,则对于M2的任意一个连通分支T,可将所有与T相邻的胞体中包含无穷远处的胞体记作该连通分支的外胞体O(T)。对于任意异于T的连通分支T′,找到T′中到T距离最短的点v(T,T′)。如果v(T,T′)不位于T′的外胞体且位于T的外胞体,则可将T′加入到候选集合A(T)中,找到A(T)中距离T最短的分支T0,同时将T0中包含v(T,T0)的胞体与O(T)等价。最后再将所有未做等价的外胞体等价,并标注所有胞体,如图11所示。

图11 标记胞体
3.2 建立虚拟流形块
步骤 4.因为输入的网格可能是非封闭的,文献[13]中计算环绕数的方法并不适用。如图 12所示,当从外胞体穿过流形块p进入胞体C时,因为p∈A却∉B,所以按照文献[13]胞体C关于B的环绕数应与外胞体的环绕数相同,而外胞体的环绕数为0,但胞体C的关于B的环绕数应为1。基于上述原因,本文建立虚拟流形块来封闭胞体的具体规则如下:

图12 穿过p计算C的环绕数
对于任意一个胞体C,用P(C)表示所有与C相邻的流形块的集合。对于任意流形块p∈P(C),用(p)表示p所在的初始输入网格,并令(C) ={(p)|p∈P(C)}。那么对于任意M0∈(C)且M0≠(p),总存在流形块p0使得(p0) =M0。如果p0的负方向刚好指向C,则可新建一个虚拟的流形块p′=p。如果p的正方向指向C,则翻转p′使得p′的负方向指向C。最后,令p′所在的输入网格为M0,即(p′)=M0。如图13所示。建立虚拟流形块的算法可用如下伪代码表示:

图13 建立虚拟的流形块
ForpinP(C):
Ifp0的负方向指向C:
p′=p
Ifp的正方向指向C:
翻转p′

3.3 计算环绕数
步骤5.首先,将连接无穷远处的胞体关于任何网格的环绕数记为0。假定胞体C的环绕数W(C)已知,用P(C,C′)表示从胞体C到胞体C′需要穿过的流形块的集合。对于任意p∈P(C,C′),如果穿过p且从正方向到负方向,则W(C′)加上1,否则减去1。
如图14所示,假定已知胞体C0关于网格A的环绕数WA(C0)=0,关于B的环绕数为WB(C0)=1。需要计算C1关于A和B的环绕数WA(C1)和WB(C1)。从C0到C1需要穿过3个流形块,其中一个属于网格A(红色,记为p0),2个属于网格B(绿色,记为p1和p2)。穿过p0为从正方向到负方向,所以WA(C1) =WA(C0)+1=1。而穿过p1为从负方向到正方向,穿过p2为从正方向到负方向,所以WB(C1)=WB(C0)+(- 1 )+ 1 =1。

图14 计算环绕数
3.4 输出结果
步骤 6.计算完所有胞体的环绕数后,可以根据得到的环绕数及布尔运算的类型决定保留、翻转或舍弃f∈M2。最后保留的三角形形成最终的输出网格。
当一个胞体C关于输入网格M的环绕数大于0,则表示胞体C在M的内部,否则在外部。当进行A-B布尔运算时,希望保留那些在A内部但在B外部的胞体。所以对每个胞体有如下保留规则:
当进行布尔并时:

当进行布尔交时

当进行布尔减时

每一个流形块p与2个胞体相邻,当2个胞体同时保留或舍弃时,则流形块p不能作为输出实体的边界,所以应舍弃。因此,当一个流形块若被保留,则其相邻的2个胞体必须有互斥的保留属性。流形块保留的具体规则为舍弃(s,s)、翻转(s,n)、保留(n,s)、舍弃(n,n),其中s为保留胞体,n为舍弃胞体,括号内第一个值为p正方向胞体是否保留,第二个值为p负方向胞体是否保留。
4 实验结果
实验在Ubuntu19.04下进行的。实验所采用的CPU是Intel i5 6500,算法由C++实现,使用的C++编译器为g++8.3。
对于有边界的非封闭网格,也能像实体一样进行布尔运算。图15为对2个有边界(已用绿色标出)的网格进行交并差后的结果。

图15 非封闭网格的布尔运算
通过布尔运算可做一些有趣的事情,如图 16所示,让塑像A和抛物面B做布尔并后,就像是给塑像加上了一顶帽子。
图17同Campen的算法[8],将不同分辨率的塑像网格旋转90°并与原网格做布尔并。本文算法能得到拓扑良好的输出,且未产生任何非流形边。由于文献[8]未能公布源码,所以只能在不同的实验配置下进行效率上的比较。其所用的 CPU为 i7 2.67 GHz,本文所用的CPU为i5 3.2 GHz。本文选取了3种不同分辨率的网格,三角面片的个数分别为200 K,400 K及800 K,旋转90°后与自身做布尔并,最终各自的算法的所需时间见表1。从表1中可以看出,本文算法相较于Campen的算法,节省了约一半时间。

图16 给塑像加上帽子

图17 2个塑像的并

表1 本文算法与Campen算法的比较(s)
为了进一步测试本文算法的效率性,与3个著名的布尔运算开源库CGAL,Cork[17]及CARVE[18]做比较(表2)。为此,构造了面数分别为4 K,24 K,240 K及950 K的球面做布尔并运算。QuickCSG能对多个输入快速进行布尔运算[19],由于只是发布了一个预编译好的二进制文件,并未公布源码,在使用该文件进行测试时,发现极易崩溃,所以此次未能将其列入到比较中。从表2中可以看出CGAL库在效率上存在严重不足,当网格面数过多时,程序会直接崩溃;Cork库在面数较少时,性能最佳,当面数较多时,效率上有明显下降;而CARVE库则始终能高效计算;本文算法虽然在面数较少时,效率上逊于 CAEVE及 Cork,而当面数较多时,几乎与CARVE一样高效。虽然从实验数据上看,本文算法在效率上与CARVE相比并无优势,但有一个不可忽略的事实——本文算法采用了CGAL的EPECK运算核。而根据文献[20]表明,这将会导致比浮点运算慢 4~5倍。所以实际上,本文算法在架构上是优于 3种算法的。另外,只有本文算法允许输入开网格,而其他算法只能被应用到封闭网格。

表2 本文算法与3个开源库进行比较(s)
为了进一步测试本文算法的鲁棒性,构造了一张复杂的球面。如图18(a)所示,其不仅非封闭(边界已用绿色标出),而且有很多褶皱和沟壑;在图18(b)中画出了特征边,且非常不光滑。3DSMAX是一款专业的建模软件,所集成的布尔运算允许输入是开网格。采用3DS MAX对2张球面做布尔并时,其无法处理如此复杂的情形,抛出了运行错误:Invalid Boolean。而本文算法能得出正确的布尔并的结果,如图 18(c)所示。本文已将代码公布在 GitHub上(https://github.com/liukaizheng/GeneralBoolean.git)。
5 结 束 语
本文提出一种基于三角网格的布尔运算方法。通过建立虚拟流形块,可准确计算每个胞体的环绕数,进而合理判断一般网格的内外关系。因此,相比许多其他算法,本文算法能应用到更多类型的网格上,允许输入是开网格、允许有空洞、多个连通分支及自交等。此外,采用CGAL库中的EPECK运算核,能无损计算布尔运算所产生的相交元素,保证了算法的鲁棒性。经过多次实验表明,本文算法是一种鲁棒的且适用广的布尔运算算法。

图18 非封闭球面的布尔并

图19 包含相交元素的三角形
但本文算法也有一些不足之处。在算法的实现过程中,对于步骤1中三角化前的输入未做预处理。如图19所示,对这样一个包含相交元素的三角形进行三角化时,本文输入的是边AB,BC,CA,DE及AF。没有将AB分成AE及AC,也没有预先算出AF及DE的交点,而是交由 CGAL的CDT函数去做的。所以三角化函数不仅需要计算交点,而且还会生成多余的退化三角形AEC及三角形BFC等,随后还需将这些三角形过滤掉。如果进行预处理,会有效提升效率,所以在将来的工作,将考虑解决该问题。另外,在每个平面上进行三角化的工作是相互独立的,这为并行计算提供了可能,所以,后续也会考虑用GPU进行加速。
