考虑需求可拆分的共享单车调度优化研究

张建同 戴倩楠 丁烨

摘 要：   研究考虑需求可拆分的共享单车调度优化问题为可拆分单商品取送货TSP问题，考虑一辆调度车，允许调度车多次访问各站点，每次满足站点的部分需求，即允许对站点的需求进行拆分。首先，考虑到调度车容量限制，统筹安排调度车行驶路径和调度车在每个站点的取车量、送车量，使得企业的运营成本达到最优。其次，提出了一种改进的变邻域搜索算法求解上述问题，使算法在陷入局部最优解时改变邻域结构，扩大搜索范围，以此提升算法跳出局部最优解的能力，加快收敛速度。最后，用数值实验验证了算法的有效性。研究结论拓展了可拆分单商品取送货问题的相关理论，并为共享单车企业的实际运营提供决策支持。

关键词：  共享单车；路径规划；需求可拆分；改进变邻域算法

中图分类号：  F 572

文献标志码：   A

Optimization of Distribution of Ofo BikesConsidering Split-Demand

ZHANG Jiantong DAI Qiannan DING Ye

（School of Economics and Management， Tongji University， Shanghai 200092， China）

Abstract：  This research studies the static bike rebalancing problem considering split-demand which can be viewed as split-demand one-commodity pickup and delivery traveling salesman problem， considering a shunting vehicle， where multiple visits are allowed to be performed at each node， i.e.， the demand for nodes is allowed to be split. The capacity limitation of the shunting vehicle is considered， and the driving path of the shunting vehicle and the amount of the vehicle fetching and delivering at each station are generally arranged， so as to make the operation cost of the enterprise optimal. Secondly， an improved variable neighborhood search algorithm is proposed to solve the problem above， when the algorithm falls into the local optimal solution， the neighborhood structure is changed and the search range is expanded， so as to improve the algorithms ability to jump out of the local optimal solution and speed up the convergence speed. Finally， numerical experiments verify the effectiveness of the algorithm. This research expands the relevant theories of split-demand one-commodity pickup and delivery traveling salesman problem， and provides decision support for the actual operation of bike-sharing companies.

Key words：  free-floating sharing bike；vehicle routing problem；split-demand；improved variable neighborhood search algorithm

作为“共享经济”领域最热的一类产品，共享单车的出现很好地解决了城市出行的“最后一公里”问题。目前共享单车进入稳步发展阶段，后续市场竞争模式从增量竞争转向存量竞争，从扩张转为精细化运营。当前共享单车市场处于稳定期，而随着碳中和、健康出行等倡议以及用户逐渐适应市场，共享单车的用户规模将有一个上升空间。与此同时单车供需不匹配的问题也日益凸显，企业在各大城市投放的共享单车量已超过理论上的需求量，然而调查显示，共享单车的潮汐现象严重。在工作日早高峰时段，交通枢纽吸引了大量的车辆停靠，严重影响周围的交通通行，这些单车在平峰时段处于暂时闲置状态，并且造成了局部地区车辆不足的问题；在晚高峰时段单车向各个居民区流动，导致交通枢纽的共享单车供不应求。该现象其实是供与求在时间、空间上不相匹配的问题。这就要求共享单车企业进行有效的调度操作。

在共享单车调度的过程中，调度车从调度中心出发，逐个访问站点，并且根据站点的需求进行取送货操作，最后返回调度中心。由于在实际中会出现站点单车的需求量超过调度车最大承载量的情况，因此允许调度车多次访问站点满足需求更符合实际。共享单车企业需统筹安排调度车的行驶路径及其在每个站点取送的单车数量，以減少时间和路程的浪费。

基于企业实际运营特征，以上调度问题可定义为考虑需求可拆分的共享单车调度优化问题（Static Bike-sharing Rebalancing Problem Considering Split-demand， SBRPSD）。该问题假设各站点的需求量，调度车在各站点间的行驶时间、服务时间确定并已知，考虑一辆调度车，允许调度车对每个站点进行多次访问，即允许对各站点的需求进行拆分，通过确定一条可行的调度车路径和调度车在每个站点的取车量、送车量使得目标函数达到最优。SBRPSD松弛了单商品取送货TSP问题（One Commodity Pickup-and-Delivery TSP， 1-PDTSP）中各站点仅允许调度车访问一次的约束，使得每个站点的取车量、送车量在模型中也作为决策变量呈现。决策变量的增加意味着 SBRPSD 问题的解空间比传统的 VRP 问题更大，因此比传统的车辆路径问题（VRP）更为复杂，属于NP-hard问题。

共享单车兴起于半世纪之前，近十年时间在世界范围内开始流行起来。起初的形式是有桩式共享单车（Station-Based Bike Sharing，SBBS）。Chemla等对有桩式共享单车调度问题进行了详细的描述，初次建立数学模型，并用分支定界算法进行求解，其中通过用禁忌搜索算法基于一定的规则得到上界，通过求解松弛问题得到下界，并用随机生成的算例验证了模型及算法的有效性。Raviv等首次提出需求部分满足的概念，他们指出，在实际情况中由于调度时间的限制以及存在供不应求的可能性，完全满足需求很难实现，因此提出以最小化总惩罚成本和总调度成本的加权和为目标函数的两个数学模型，其中一个模型不允许各站点暂存自行车、被调度车多次访问，而另一个模型允许，并对两个模型的求解结果进行对比。DellAmico为该问题建立了 4 个混合整数规划模型，用分支定界算法分别对它们进行求解，并对比结果。Erdogan通过将普通整数变量转换为二元变量建立整数规划模型，并通过计算实验发现站点可以暂存自行车的公共自行车调度问题比不能暂存的更易求解。

随着时代的發展进步，有桩式公共自行车演变成了无桩自由式共享单车（Free-Floating Bike Sharing，FFBS）。Pal等旨在高效地解决静态再平衡问题，提出了一种具有变邻域下降算法的混合嵌套大邻域搜索，在算例验证中，提出所用算法优于禁忌搜索算法，并且能够处理与 FFBS 和 SBBS 相关的规模不断增加的静态重新平衡问题，同时在合理的 CPU 时间内可获得高质量的解决方案。Schuijbroek基于先聚类后路径规划的思想，建立了基于聚类问题的混合整数规划模型，该模型将多调度车问题为单调度车问题进行求解，并提出相应的启发式算法进行求解。Hernandez-Perez描述了一种元启发式算法，它用一组站点代表每个客户，每个站点都与潜在访问相关联，将每个客户需求分解为与其站点相关的部分需求，并用变邻域搜索解决单一商品取送货旅行商问题。Polat等提出了一个混合整数数学优化模型和一个基于扰动的邻域搜索算法，并结合经典的节约启发式算法，计算结果表明，与文献报道的方法相比，所提出的方法对一些著名的基准问题产生了更优的解，对其余的测试问题产生了相当好的解。Cruz和Ho等都在算法上取得了突破。

综上，共享单车调度优化问题的模型已有大量研究， 但是考虑需求可拆分的相关问题研究较少。并且，改进的变邻域搜索算法在共享单车调度优化问题方面的应用研究较少。因此，本研究考虑需求可拆分的共享单车调度优化问题，允许调度车在每个站点执行多次访问，并设计一种改进的变邻域搜索算法，使算法在陷入局部最优解时改变邻域结构，更换搜索范围，以此提升算法跳出局部最优解的能力，加快收敛速度，数值实验验证了算法的有效性。

1 模型建立

1.1 问题定义

SBRPSD定义如下：考虑一组有限的节点，假设节点之间的距离（或成本）已知。若某节点单车过多需要调度车运走，则该节点具有负需求，为取货点；若某节点单车过少需要补充，则该节点具有正需求，为送货点。假设有一辆有容量限制的车辆从调度中心出发分别访问各节点并根据节点需求取、送单车后再返回节点，各节点至少被访问一次，至多被访问两次，选择合适的路径并满足节点的需求。重置目标可分为完全重置和部分重置，完全重置要求所有节点的单车存量对于需求量，考虑到完全重置的运营成本过高，因此目标函数中除了考虑最小化行驶距离，同时要考虑最小化未满足需求的惩罚成本。根据问题定义，对模型进行如下假设：

1）调度中心只有一个，调度中心、节点的坐标位置和需求已知且固定，不考虑运输中交通状况的影响。

2）每个节点至少访问一次，至多访问两次。

3）调度车服务时的载重不可超过其最大承载量。

4）调度车从调度中心出发并最终返回调度中心，且服务开始前和结束后调度车的载重均为0。

1.2 数学模型

定义G=（V，A）为一个完全图。V={0}∪（VC）表示网络节点集合，其中0表示调度中心；VC=∪i∈I Vi表示调度车对各站点的访问节点，I={1，…，n}表示站点集合，Vi={i1，i2 }，i∈I表示调度车对站点i的第一次访问和第二次访问；A={（v，w）│v∈V，w∈V，v≠w}表示网络中的弧集；对于SV，δ+（S）={（v，w）│v∈S，wS}，δ-（S）={（v，w）│vS，w∈S}。

模型变量及参数的含义为：

Ca：给定弧a=（v，w），调度车从节点v到节点w的路径成本。

φ：节点需求未满足的惩罚成本。

pi：调度开始前节点i的单车数量。

p′i：调度结束后节点i期望的单车数量。

di：di=p′i-pi，表示节点i的需求，di>0表示节点i需要运来di辆单车（对应于送货点），di<0表示节点i运走di辆单车（对应于取货点），假设∑i∈Idi =0。

Q：调度车的最大承载量。

决策变量为：

xa：0-1变量，若调度车经过弧a时为1，否则为0。

yv：0-1变量，当路径访问节点v时为1，否则为0。

fa：非负变量，调度车经过弧a时的载重。

gv：整数变量，调度车在节点v取货量（gv<0）或送货量（gv>0）。VP={v|gv<0}表示取货点集合，VD={v|gv>0}表示送货点集合。

SD1PDTSP的数学模型可以表示为：

min∑  α∈A ca xa+φ∑  i∈I |di-gi1-gi2| （1）

s.t.

yi1=1，i∈I （2）

y0=1 （3）

∑a∈δ+（v）xa=∑a∈δ- （v）xa=yv， v∈V （4）

∑a∈δ+ （S）xa≥yv+yw-1， SV，v∈S， w∈V＼S （5）

∑a∈δ-（v）fa-∑a∈δ+（v）fa=gv， v∈V （6）

0≤fa≤Qxa， a∈A （7）

pi+gi1≥0， v∈V （8）

pi+gi1+gi2≥0， v∈V （9）

yv，xa∈{0，1}， v∈V，a∈A （10）

其中：式（1）是本文的目标函数，它由调度工作的固定成本、运输成本以及惩罚成本组成；式（2）（3）确保每个节点均被调度车访问；式（4）表示车辆流平衡约束；式（5）确保路径连通；式（6）表示调度车在节点v取走（或投放）的数量等于调度车离开节点v后的载重减去调度车到达节点v前的载重；式（7）确保了调度车装载量非负且小于调度车最大承载量；式（8）、（9）确保各节点的单车存储量大等于0，并且确保各节点的第一次访问先于第二次访问。

2 算法

2.1 算法原理和实现步骤

变邻域搜索算法（VNS）的基本思想是通过局部搜索算法求得局部最優解，利用不同的动作构成的邻域结构进行交替搜索，在集中性和疏散性之间达到很好的平衡。它能够在当前邻域中找到最优解，又能跳出当前邻域寻找更好的解，然而变邻域搜索算法存在收敛速度慢的问题，解的质量依赖合适的邻域结构集合。

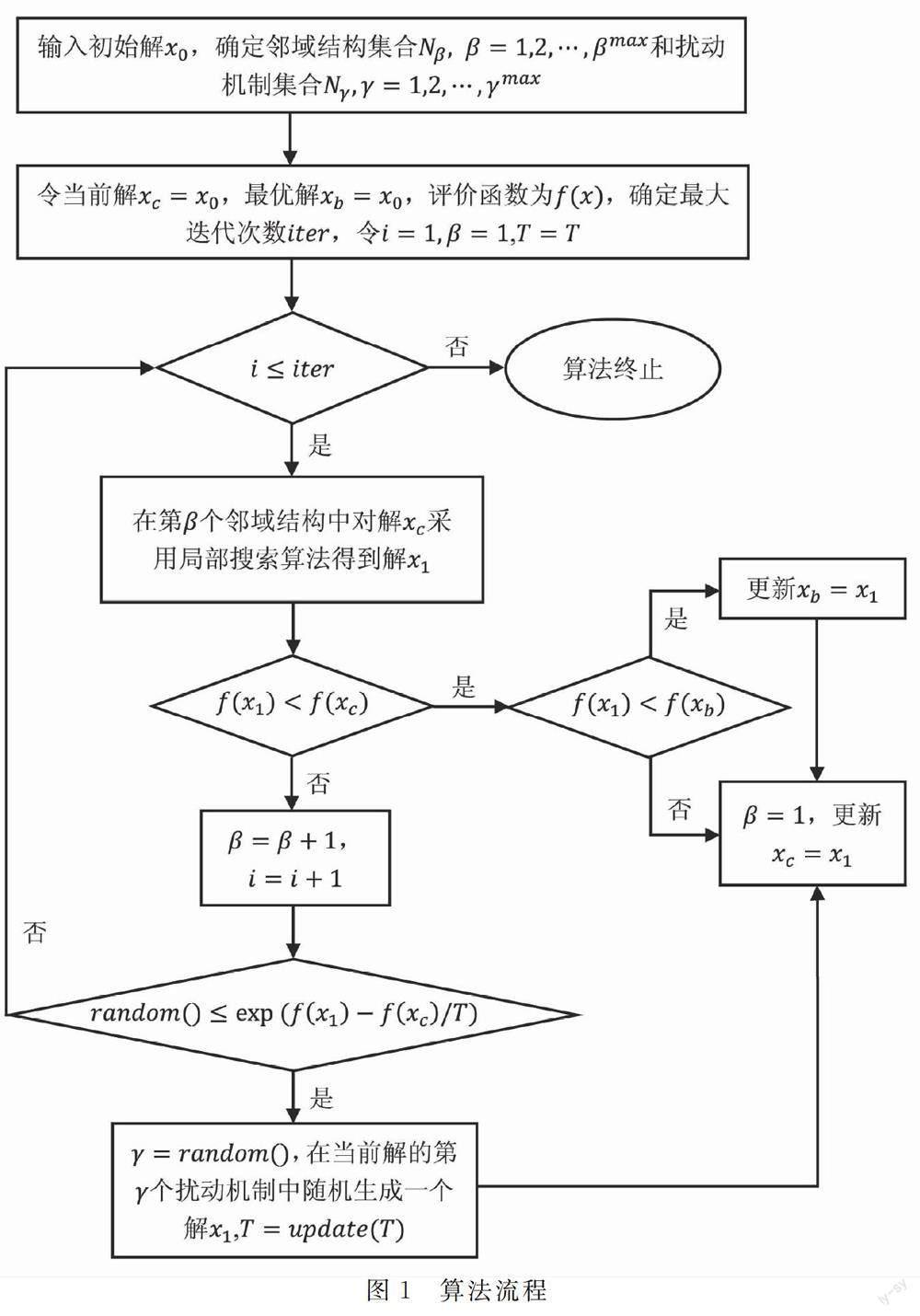
为提升算法扰动性，本文提出改进变邻域搜索算法（IVNS），在传统邻域结构的基础上，结合局部搜索和扰动机制，并且引入模拟退火算法的解接受准则， 以一定概率接受较差的解。算法的具体流程见图1。首先随机生成一个初始解。接下来，连续应用局部搜索、扰动机制，直到满足停止标准。也就是说，当前解在某个邻域结构中无法找到更好的解时以一定的概率激活扰动机制，从而跳出局部最优。

2.2 拆分节点需求（SplitVertex）

本文引入了一个名为SplitVertex的过程，对需求未完全满足的节点进行额外访问。具体来说分别选择了取货和送货情况下最不平衡的节点i和j，并且有两种添加方式：（i）在节点j之后添加弧（j，i） 和（i，j）；（ii）在节点i之后添加弧（i，j）和（j，i）。

图2通过例子祥细地描述了该过程，其中17号节点和9号节点是最不平衡的。17号节点初始有20辆单车，需要取走10辆，即一个取货点，而9号节点初始没有车，需要送来10辆，即一个送货点。图2（a）给出了一个可行的解决方案，然而节点的需求没有得到满足，因为17号节点只取走了4辆自行车，9号节点送来了4辆自行车。图2（b）显示了一种改进的解决方案，添加弧（9，17）和（17，9）后可以观察到，第二次访问是对第一次访问的补充，满足了两个节点的需求：车辆在9号节点送来1辆，其余7辆在17号节点取走，现已平衡，最后通过送来6辆自行车满足9号节点的需求。

2.3 邻域结构集合和扰动机制设计

2.3.1 邻域结构集合设计

在局部搜索过程中，初始解和扰动解可以通过基于变邻域下降（VND）的过程得到改进。VND系统地检查不同类型的邻域，如果邻域产生一个更好的解，那么更新当前解并且从第一个邻域开始继续搜索，否则将在下一个邻域进行搜索，当所有邻域都无法完善当前解时，该过程结束。

本文共设计5个邻域结构，具体如下：（1）Swap，交换两个节点的序列；（2）Reinsertion，移除一个节点，将其重新插入序列的其他位置；（3）Or_opt2，移除两个连续的节点，将其重新插入序列的其他位置；（4）Suppression，移除节点的第二次访问；（5）SplitVertex，拆分节点需求。表1详细地展示了初始解为0-8-7-1-5-3-4-2-6-2-9-0时每个邻域结构的过程，为便于说明，省略了取送货操作值以及车辆负载。例如，初始解在Suppression邻域结构中移除节点2的第二次访问，得到了新的解0-8-7-1-5-3-4-2-6-9-0。

表1详细地展示了邻域结构的组成过程，其中初始解为0-8-7-1-5-3-4-2-6-2-9-0。

2.3.2 扰动机制设计

每当算法进入扰动机制时，随机选择以下两种机制：（1）Or_opt3——移除三个连续的节点，将其重新插入序列的其他位置；（2）Suppression——移除节点的第二次访问。

2.4 解接受规则

为进一步平衡算法的收敛速度与扰动性，引入模拟退火算法的解接受准则，以一定概率接受较差的解，在某个邻域结构中无法找到更好的解时以一定的概率激活扰动机制，从而跳出局部最优，扰动机制激活的频率随着迭代次数的增加而降低。假定当前解xc经过VND得到x1，当f（x1）>f（xc）时，以一定概率接受x1。初始状态为T0，冷却系数为θ，温度更新为T=T0，其中0<θ<1，θ越接近0温度下降越快，反之越慢。

2.5 算法终止准则

由于变邻域搜索算法与其他现代优化算法一样，并不能保证找到问题的全局最优解，所以需要另外给出终止条件来停止搜索。常用的终止准则有设置最大迭代次数、设置终止温度Tf、设置当前最优解保持不变的最大迭代次数等。本文采用的方法是设置当前最优解保持不变的最大迭代次数，即如果当前的最优解在迭代了设定值次数后还没有找到更好的解，那么认为算法收敛，并终止算法。

3 数值实验仿真

3.1 测试环境

本文算法测试采用C++编码通过Visual Studio Code实现，在主频3.2Ghz、内存8G的计算机上进行。

3.2 测试算例

为测试算法的有效性，本文结合共享单车实际运营情况， 采用以下方法生成算例。节点坐标在［-100，100］范围内随机生成，调度车容量为20，节点需求为［-35，35］范围内的整数，并且所有节点的需求之和为0。对于节点规模，考虑三类：小规模的节点数为30，中等规模的节点数为50，大规模的节点数为100。每个规模各有10个算例，命名为A～J。

3.3 参数设定及参数寻优

改进变邻域算法的初始状态T0取值范围可参照模拟退火算法，一般取1000、2000、3000、4000等，温度更新函数中的冷却系数θ一般取0. 9、0. 95、0. 98等，当前最优解保持不变的最大迭代次数iter根据问题类型的不同可取200至2000不等。

为了更合理地设置算法的参数，本文通过对节点规模为30的十个算例的计算进行参数寻优。首先，令iter=500，冷却系数θ= 0. 95，取T0为1000、2000、3000、4000，计算结果如表2所示，当T0=3000时，算法求得的最优值最小且运行时间较短，所以取T0=3000。其次，令T0=3000，iter=500，取θ为0.9、0. 95、0.98，计算结果如表3所示，当θ=0.95时，算法求得的最优值最小，因此取θ=0.95。最后，在以上参数给定的基础上，取iter为500、1000、1500，计算结果如表4所示，当iter=1500时所得最优值最小，因此取iter=1500。

3.4 算法有效性检验

为验证改进变邻域算法的有效性，本文将IVNS算法与传统VNS算法进行对比实验。其中，VNS的扰动机制与IVNS相同，VNS 算法的局部搜索过程对扰动机制中产生的当前解分别进行局部搜索，采用Swap算子或Or-opt2算子，其余参数设置相同。

本文运用IVNS和VNS分别对上述30个算例进行求解，两种算法对每个算例进行10轮求解，结果如表5、表6所示。其中，表5展示了两种算法对30个算例的求解结果最优值及其对应 CPU 时间，表6展示了两种算法对30个算例求解结果的平均值及标准差。

通过表5求解结果比较可知，IVSN算法求得的最优值优于VNS算法，IVNS求解中型算例速度很快，但当算例规模扩大到100时求解时间急剧增加，可见算法扰动性的增加一方面能提高解的质量但同时也花费了更久的CPU时间，但仍在可接受的范围内，可见IVSN算法可以在合理的时间内求得高质量的解。此外，通过表5求解结果比较可知，IVNS算法的平均值和标准差都更优，说明使用IVNS能够更稳定地获得更优的解。

4 结语

本文对共享单车调度优化问题模型进行扩展，松弛了站点仅访问一次这一条件，允许拆分站点的需求使调度车能够对站点进行两次访问，令问题更具实际意义，拓展了共享单车调度优化问题理论研究，并为共享单车企业管理运营提供决策支持。本文还设计一种改进变邻域算法，将模拟退火算法的解接受准则引入其中，以增强算法扰动性、扩大搜索范围跳出局部最优解，并在后续的数值实验中验证了该算法的有效性和稳定性。同时，本文研究的问题及采用的方法还有待提升。一方面，该模型可扩展到多辆车、时间窗限制等，也可考虑将其中的站点作为中转站使其暂时超过或不满足其需求；另一方面，改进变邻域搜索算法在本文中起到了良好的作用，但仍可以尝试与其他方法如启发式算法、机器学习等结合，以更好地求解该问题。

参考文献：

［1］  王涵霄.考慮维修的共享单车调度优化研究［J］. 工业工程与管理， 2019，24（2）：31-37.

［2］ CHEMLA D. Bike sharing systems： solving the static rebalancing problem［J］. Discrete Optimization， 2013，10（2）： 120-146.

［3］ RAVIV T， TZUR M， FORMA I A. Static repositioning in a bike-sharing system： models and solution approaches［J］. EURO Journal on Transportation and Logistics， 2013，2（3）： 187-229.

［4］ DELL′AMICO M. The bike sharing rebalancing problem： mathematical formulations and benchmark instances［J］. Omega-International Journal of Management Science， 2014（45）： 7-19.

［5］ ERDOGAN G. An exact algorithm for the static rebalancing problem arising in bicycle sharing systems［J］. European Journal of Operational Research， 2015， 245（3）： 667-679.

［6］ PAL A， ZHANG Y. Free-floating bike sharing： solving real-life large-scale static rebalancing problems［J］. Transportation Research Part C-Emerging Technologies， 2017（80）： 92-116.

［7］ SCHUIJBROEK J. Inventory rebalancing and vehicle routing in bike sharing systems［J］. European Journal of Operational Research， 2017，257（3）： 992-1004.

［8］ HERNANDEZ-PEREZ H.  Heuristic algorithm for the split-demand one-commodity pickup-and-delivery travelling salesman problem［J］. Computers & Operations Research， 2018（97）： 1-17.

［9］ POLAT O. A perturbation based variable neighborhood search heuristic for solving the vehicle routing problem with simultaneous pickup and delivery with time limit［J］. European Journal of Operational Research， 2015，242（2）： 369-382.

［10］ CRUZ F. A heuristic algorithm for a single vehicle static bike sharing， rebalancing problem［J］. Computers & Operations Research， 2017（79）： 19-33.

［11］ HO S C， SZETO W Y. A hybrid large neighborhood search for the static multi-vehicle bike-repositioning problem［J］. Transportation Research Part B-Methodological， 2017（95）： 340-363.

［12］ 張建同，丁烨. 变邻域模拟退火算法求解速度时变的VRPTW问题［J］. 运筹与管理，2019，28（11）：77-84.

［13］ 徐东洋，李昆鹏，郑飘，等. 多车场多车型多品类供需未匹配与可任意拆分取送货车辆路径问题优化［J］. 管理学报，2020，17（7）：1086-1095.