基于单元整体教学设计的实践研究

金国年

［摘  要］ 文章以“三角形”单元教学为例，提出如下教学策略：研究一个三角形的基本要素、性质时，注重研究方法的迁移，进行教学内容之间的横向连续和不同年级的纵向递进相结合的整体单元设计；研究两个三角形的关系时，注重自上而下的整体式学习，建构图形知识学习的整体框架性结构；在全等三角形的基本构图中，注重知识的有机融合，凸显多单元融合的整体教学设计.

［关键词］ 单元整体；三角形；单元教学设计

？摇《义务教育数学课程标准（2022年版）》指出：“在数学教学中要重视单元整体教学设计：改变过于注重以课时为单位的教学设计，推进单元整体教学设计，体现数学知识之间的内在逻辑关系，以及学习内容与核心素养表现的关联.  ［1］ ”单元整体教学设计要整体分析数学内容本质和学生认知规律，合理整合教学内容，分析“主题—单元—课时”的数学知识和核心素养主要表现，确定单元教学目标，并落实到教学活动的各个环节，整体设计，分步实施，促进学生对数学教学内容的整体理解与把握，逐步培养学生的核心素养  ［2］ . 本文将基于单元整体教学设计的视角，以北师大版七年级下册“三角形”为例，探索三角形单元教学的课时设计，从而更好地体现数学知识之间的内在逻辑关系，真正促进学生核心素养的形成.

单元内容教学分析

北师大版七年级下册“三角形”包括两部分内容：一是理论知识，即三角形的基本要素及基本性质；二是实践运用，即三角形全等的条件和三角形全等的应用. 学习这部分内容之前，学生在“相交线与平行线”的学习中已对图形有一定的认识，形成了较好的几何直观与推理能力，这都为三角形知识的学习做了良好的铺垫. 三角形是初中数学第一个系统研究的几何图形，因此本节课的学习方法对后续几何图形的研究有着十分重要的指导作用. 基于以上分析，实施本单元的教学时，教师需要着重解决下面几个问题：（1）使学生掌握用数学的方法和思维去研究几何图形；（2）在探索三角形全等条件的过程中，如何更好地发展学生的空间观念和几何直观；（3）如何将三角形性质的研究迁移到后续四边形的研究，体现不同年级的纵向递进整体单元设计；（4）如何将全等三角形的研究迁移到相似三角形的研究，建构图形知识学习的整体框架性结构.

单元整体教学建议

“三角形”包括两大内容：一是研究一个图形的基本要素，二是研究两个图形（即全等三角形）之间的关系. 这两部分相互衔接，由静态到动态. 教师进行教学设计时，要把重点放在“让学生对三角形知识点形成整体认知，充分理解不同知识点之间的关联性，使不同教学内容之间建构成一个有机整体”上. 教学本单元时，教师可参考如下教学建议.

1. 研究一个三角形的基本要素、性质时，注重研究方法的迁移，进行教学内容之间的横向连续和不同年级的纵向递进相结合的整体单元设计

对于几何图形的学习，初中数学主要研究三角形和四边形的性质. 对于一个图形性质的研究，首先要研究它的基本要素. 图形的基本要素主要围绕两个关系展开：一是边与角的关系，二是图形内部特殊线段（如角平分线、中线、高）的关系. 这里的关系包括数量关系和位置关系. 三角形是多边形中最简单的图形，也是初中数学第一个系统研究的几何图形，如果教师能在本单元的教学过程中有效地整体渗透研究一个图形性质的方法，那么学生在以后的学习中便能自觉地将本单元的知识与其他同类知识贯通. 学生对本单元知识的掌握程度直接影响后续几何图形的学习，所以教师进行单元教学设计时，既要体现教学内容之间的横向连续，也要体现不同年级的纵向递进.

2. 研究两个三角形的关系时，注重自上而下的整体式学习，建构图形知识学习的整体框架性结构

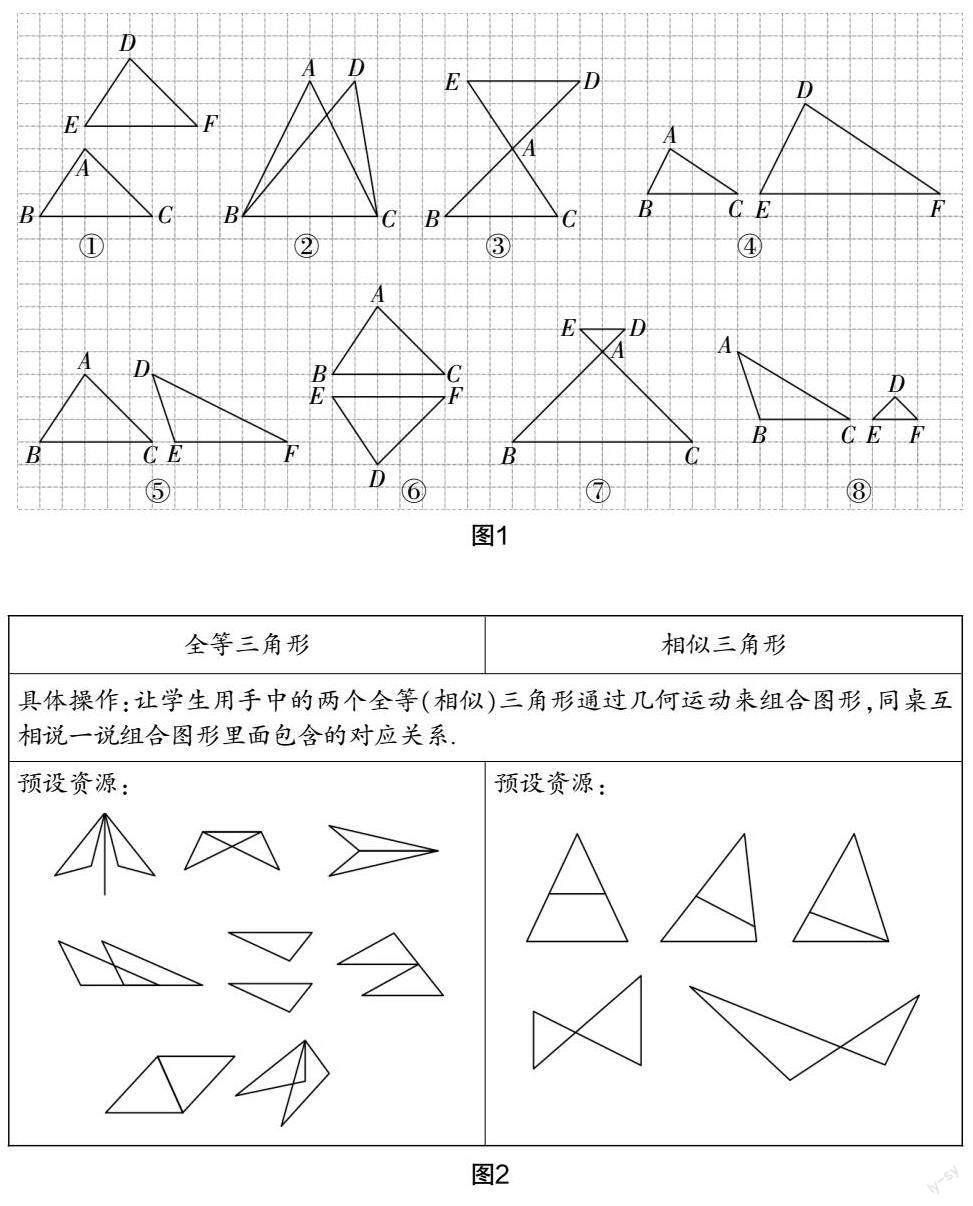
北师大版教材对于两个三角形的关系（全等三角形）的概念的引出，采取的方式是先学习全等图形的概念，从而类比得到. 但是，对于两个三角形之间的关系，我们不仅仅只学习全等关系. 所以为了更好地让学生形成图形知识学习的整体框架性结构，教师进行教学设计时应采用自上而下的整体教学设计，即帮助学生从整体角度理解两个三角形之间的不同关系，包括以下几种（如图1所示）：（1）全等关系，即形状相同，大小相等；（2）等积关系，即形状不同，大小相等；（3）一般关系，即形状不同，大小不等，这种关系一般不研究；（4）相似关系，即形状相同，大小不等  ［3］ .

当学生对分类有整体把握之后，教师再引导学生学习下位概念，即全等三角形和相似三角形. 自上而下的整体性设计可以帮助学生对教学内容形成结构化认识，这样的学习是整体式的，而不是片段式、零碎的或点状的，能使学生的知识点形成整体性框架. 从全等三角形的学习到相似三角形的学习，学生能形成三角形知识学习的整体框架性结构.

3. 在全等三角形的基本构图中，注重知识的有机融合，凸显多单元融合的整体教学设计

等学生掌握了不同类型的三角形的性质和判定后，教師可以通过学生感兴趣的活动来开展教学，如从运动的角度看待不同三角形之间的关系，激发学生对教学内容的兴趣和积极参与度，同时对全等三角形和相似三角形的基本构图有进一步的认识  ［3］ ，如图2所示.

整体教学设计可以使学生直观地、整体地认识变化前后图形之间的关系及图形的变换，能帮助学生从点状学习调整为整体学习，能提升学生的想象能力，且能较好地向学生渗透数学模型思想方法. 将全等三角形、相似三角形和图形变换三个教学内容整合、融合起来，凸显了“整体性”，形成了多单元的整体教学设计.

单元整体教学实践

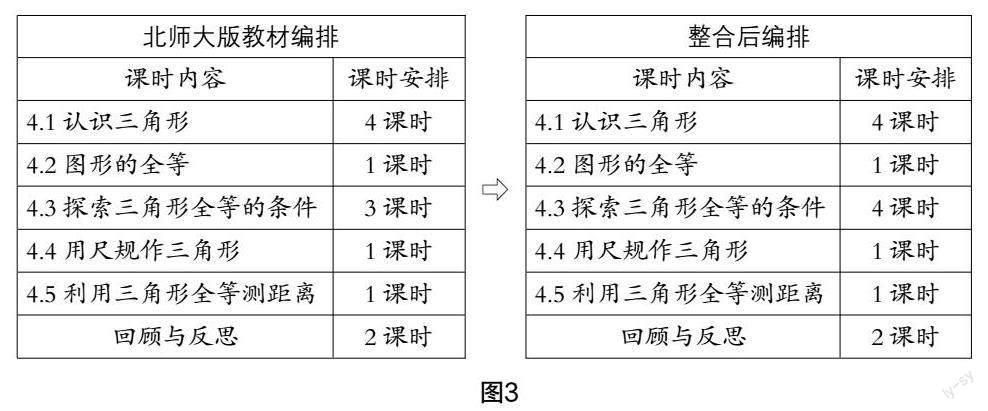
在北师大版教材的编排中，“三角形”这一单元共12个课时，为了更好地让学生对三角形形成整体认识，教师教学时可将12个课时整合成13个课时，具体安排如图3所示.

结合教学建议和课时编排，下面对“三角形”单元教学内容的整合后编排进行说明：

在“4.1 认识三角形”中，总课时不变，但对第3课时和第4课时进行了整合，改变了教材中第3课时学习角平分线与中线的概念与性质，第4课时学习高的概念与性质的编排方式. 整合后“4.1 认识三角形”第3课时和第4课时的安排为：第3课时整体学习角平分线、中线以及高的相关知识，因为这三条线是三角形内部的特殊线段，教师可引导学生先从整体上认识并能自觉地进行对比分析；第4课时则一起探究内部三条特殊线段的性质. 这样的整体设计有利于学生的认知结构化，凸显了整体框架性结构.

在“4.2 图形的全等”中，教材采取的方式是先学习全等图形的概念，再通过类比得到全等三角形的概念和性质. 设计教学时，我们主张让学生先从上位概念出发，认识全等三角形，也就是说，让学生先从整体上理解两个三角形可能存在的关系——全等关系、等积关系、一般关系、相似关系. 学生对上位概念有了一定的认识之后，再开始学习下位概念，即全等三角形. 这样能让学生的知识组块化、群集化，这也是我们所强调的整体框架性结构.

在“4.3 探索三角形全等的条件”中，教材采用3个课时探究两个三角形全等的判定定理. 整合后的编排，是将这一节变为4个课时：前两个课时整体探究三角形全等的4个判定定理，后两个课时在具体的问题解决中对判定定理进行灵活运用. 值得注意的是，整合后探究三角形全等的判定定理时要具有开放性，教师要鼓励学生自主探究，因此课堂上前两个课时对4个判定定理的探究是随机的，即第1个课时教师鼓励学生随机探究出2个判定定理，第2个课时教师鼓励学生探究出另外两个判定定理. 这样可以改变学生本节课学习了哪个判定定理，就只会用那个判定定理进行解题的固化思维，凸显了学习三角形全等判定的整体框架性结构.

在“回顾与反思”的第2个课时中，教师要加深学生对全等三角形基本构图的认识. 在这部分学习中，教师要引导学生自主梳理知识框架，并独立画出框架图，要让学生基于对相关重点知识的理解和掌握，对图形进行组合，如旋转、平移或翻折两个全等三角形，从而加深学生对全等三角形基本构图的认识和理解，使学生从整体上认识图形的变换，并领悟其中渗透的数学模型思想方法.

反思

“单元整体教学设计”是近几年伴随新课标出现的一个热点问题，如何合理整合教学内容，并在教学过程中贯彻执行，从而真正提升学生的素质和能力，值得我们一线教师重点探究. 上文提到的单元整体设计，不仅注重学习方法的迁移，体现横向连续的单元整体设计，同时注重知识的有机融合，体现不同年级的纵向递进，能让学生更好地建构知识学习的整体框架性结构.

參考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］吴亚萍.  中小学数学教学课型研究［M］. 福州：福建教育出版社，2014.

［3］ 何春迎. 运用“长程两段”策略实现整体教学设计的思考［J］. 中学数学研究（华南师范大学版），2020（08）：13-16.