十字形伞开伞充气过程数值仿真研究

谢淮 刘宇 王臻 昌飞

十字形伞开伞充气过程数值仿真研究

谢淮 刘宇 王臻 昌飞

（北京空间机电研究所，北京 100094）

十字形降落伞是航空航天减速领域常用的伞型，开伞充气过程是其工作过程中较为复杂的一个阶段。为了研究十字形伞开伞充气过程中的动力学特性，文章基于任意拉格朗日-欧拉方法对十字形伞开伞过程进行流固耦合仿真计算，并将计算结果与风洞试验结果进行对比。对比发现：仿真计算得到的十字形伞稳态外形与试验结果一致，且仿真获得的降落伞气动载荷历程曲线与试验结果基本相符，载荷呈现出随着开伞过程逐渐增大，在开伞结束达到最大值后略有降低并逐渐稳定的趋势。仿真结果还表明，在十字形伞开伞过程中，伞衣的最大应力点位于伞臂的中心区域，充气顺序的先后会影响伞臂的应力分布，降落伞稳定后伞衣应力呈对称分布。文章采用的仿真方法能较好地模拟十字形伞开伞充气的动力学过程，得到的伞衣应力分布特点及影响因素可为十字形伞的设计与优化提供参考。

十字形降落伞 计算流固耦合动力学 开伞 充气

0 引言

降落伞是目前航空航天领域应用最广泛的减速手段[1-2]，根据伞衣结构形式的不同，可以分为平面圆形伞、方形伞、带条伞、环帆伞以及十字形降落伞等。相较于其他伞形，十字形降落伞具有工艺简单、稳定性好、开伞动载小等优点，其独特的结构使得它在高空高速降落和复杂的气象条件下表现出色，成为众多型号任务的理想选择[3-4]，被广泛用于军事空投、紧急救援、探测器着陆以及科学实验等领域。

由于十字形伞具有独特的设计特点和广泛的应用背景，对其力学特性进行深入研究具有重要意义[5]。在降落伞方案设计中，充气过程中的力学特性[6]，包括充气时间、气动力变化以及伞衣载荷变化是需要考虑的关键因素[7]。相较于高成本的试验手段[8-10]，仿真计算方法是目前研究降落伞开伞过程动力学的有效手段[11]。

流固耦合是降落伞开伞过程仿真的核心问题，因为降落伞伞衣材料为柔性结构，同时具有透气性，这使得降落伞开伞过程流固耦合处理及其困难[12]。目前应用于降落伞开伞计算的流固耦合仿真方法有CFD-MSD（Computational Fluid Dynamics-Mass Spring Damper）方法[13]、DSD/SST（Deforming-Spatial- Domain/Stabilized Space-Time）方法[14]及浸入边界法（Immersed Boundary Method，IBM）[15]等，但是这些方法均具有局限性：CFD-MSD方法侧重于伞衣外形的计算，无法得到结构应力信息；DSD/SST方法侧重于外部流场的数值计算，难以对充气阶段进行研究；IBM侧重于固体的响应，对流场的细节计算不够精确。近些年来，商业软件LS-DYNA的流固耦合方法可以克服以上方法的缺点，满足降落伞仿真的需要，因此被广泛应用于亚声速降落伞、超声速降落伞等降落伞仿真领域[16-19]。在LS-DYNA的流固耦合（Fluid-Structure Interaction，FSI）方法中，流场单元通过任意拉格朗日-欧拉（Arbitrary Lagrange-Euler，ALE）方法进行求解，降落伞单元通过拉格朗日法进行求解，最后通过罚函数方法对流场及伞衣之间的相互作用力进行耦合计算。

本文基于ALE/FSI方法对十字形伞开伞过程进行仿真计算，并将计算结果与风洞试验结果进行对比，验证仿真模型的正确性，在此基础上分析十字形伞开伞过程中载荷变化以及伞衣内的应力分布变化的特点，从而能够更深入地理解十字形伞开伞过程动力学特性，为其设计和应用提供更准确的指导。

1 研究方法

1.1 ALE方法

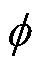
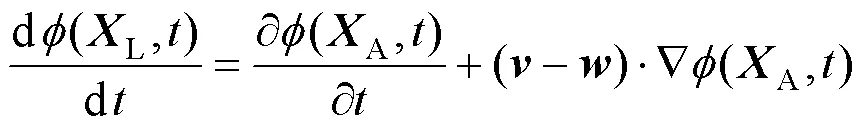
式中L为拉格朗日描述下的质点坐标；A为ALE描述下的质点坐标；和分别为质点运动速度和相应的ALE坐标点运动速度。由式（1）可以看出，当=时，有L=A，公式转变为拉格朗日形式；当=0时，右边第一项为0，公式转变为欧拉形式。

基于ALE方法的N-S方程可表示为

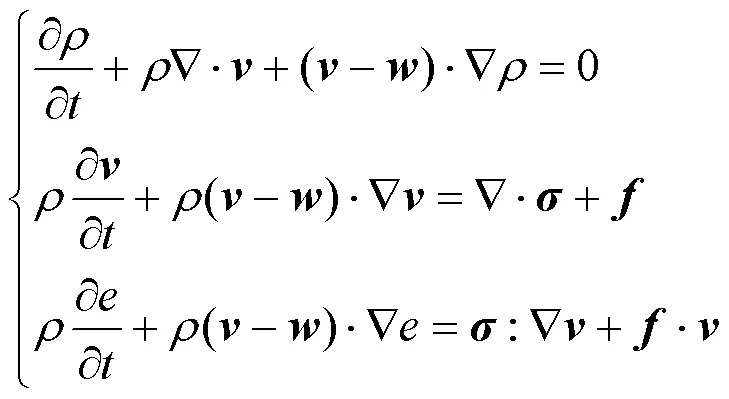
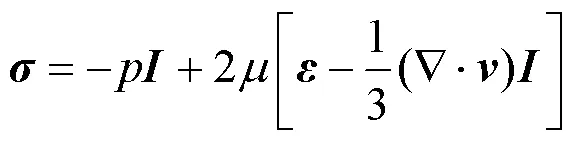
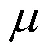
通过算子分裂的方法[23]，式（2）可以分为两步求解：拉格朗日步和输运步。首先通过一个显式有限元方法实施拉格朗日步，在该过程中网格点随流体质点运动，即在方程中令=。拉格朗日步的方程为

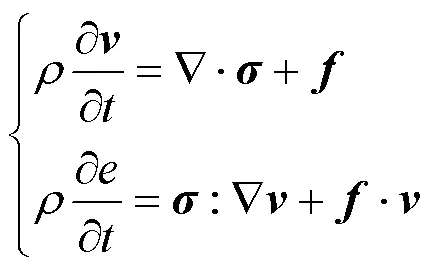
质量方程也可以通过拉格朗日法求解，但是在此可使用更简便和精确的方法

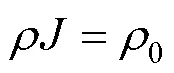
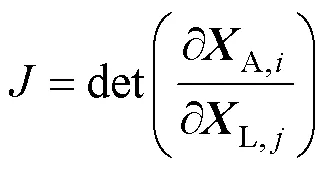
式中A,i表示矢量的第个分量，L,j表示矢量的第个分量，由于A和L均为三维矢量，故=1,2,3,=1,2,3。

接下来实施输运步，网格进行运动，质量、动量和能量均因网格运动而产生通量。在本文中，考虑网格运动回初始构型位置，即完整的ALE过程完成后网格保持不变，因此输运步的方程可表示为

1.2 结构控制方程

降落伞结构为柔性连续介质，其控制方程为

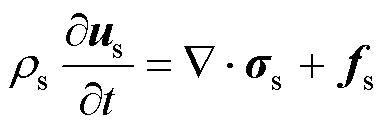
1.3 罚函数方法

在流固耦合问题中，流体与固体之间的相互作用是通过模拟两者之间的相互影响来实现的。其中一种常用的方法是罚函数方法。在罚函数法中，为了模拟接触力的相互作用，在接触节点处使用一个类似于弹簧的力模型。在该力模型中，假设存在两个接触节点，引入一个假想的“弹簧”，它对两个节点施加的力大小相等，方向相反。这个“弹簧”的作用类似于一个力的传递媒介，使得节点之间的接触力可以相互传递。当一个节点施加力到弹簧上时，弹簧会将等大、相反方向的力传递给另一节点。这种模拟接触力的处理方法实施简单，可以使得节点之间的接触行为在流固耦合问题的模拟中得到有效的考虑，同时保证了计算过程中动量及能量的守恒性。

在本文中用罚函数方法来解决两个问题：伞衣表面的相互接触（自接触）和气体与伞衣表面的接触（流固耦合）。

1.3.1 伞衣自接触

当未充满状态下伞衣受来流与伞绳共同作用发生变形时，伞衣单元之间会发生相互接触，本文使用单面接触算法模拟这一现象。以二维情况为例，定义穿透距离1为一个单元节点（Slave）与面（Master）之间的垂直距离，则

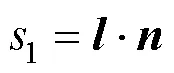
式中为面上一点到节点的矢径；为面法向量。由1的定义可知，当1= 0时，节点与面发生接触，当1<0时，节点与面发生穿透。

当穿透发生时，定义约束力1为

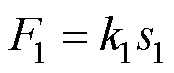
式中1为刚度系数。

1.3.2 流固耦合

在流固耦合模型中，流体单元为三维ALE实体单元，伞衣单元为二维拉格朗日壳单元，流体单元与伞衣单元之间同样通过罚函数法耦合来传递作用力。当拉格朗日单元与ALE单元之间相对运动时，将拉格朗日单元节点视为从节点，不考虑网格运动的ALE描述与拉格朗日描述的单元节点坐标相等，考虑网格运动后可进行计算得到主节点，定义穿透位移2为

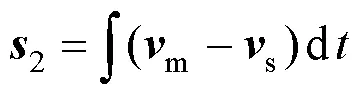
式中m，s分别为主节点及从节点运动速度。耦合的作用力定义为

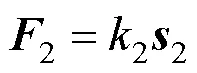
式中2为耦合刚度系数。

1.4 伞衣透气性方程

织物透气量对伞衣充气过程影响很大，而在充气过程中随着伞衣的内外压力差变化，织物透气量也产生变化。伞衣的透气速率与伞衣两侧压差的关系可由经验公式表示为[24]

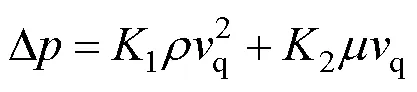
2 数值计算模型

2.1 研究对象

根据试验任务，本文仿真计算所使用十字形伞外形尺寸如图1所示。降落伞的材料选用织物透气性参数为1=35.4和2=5.29×106/m的锦丝绸。

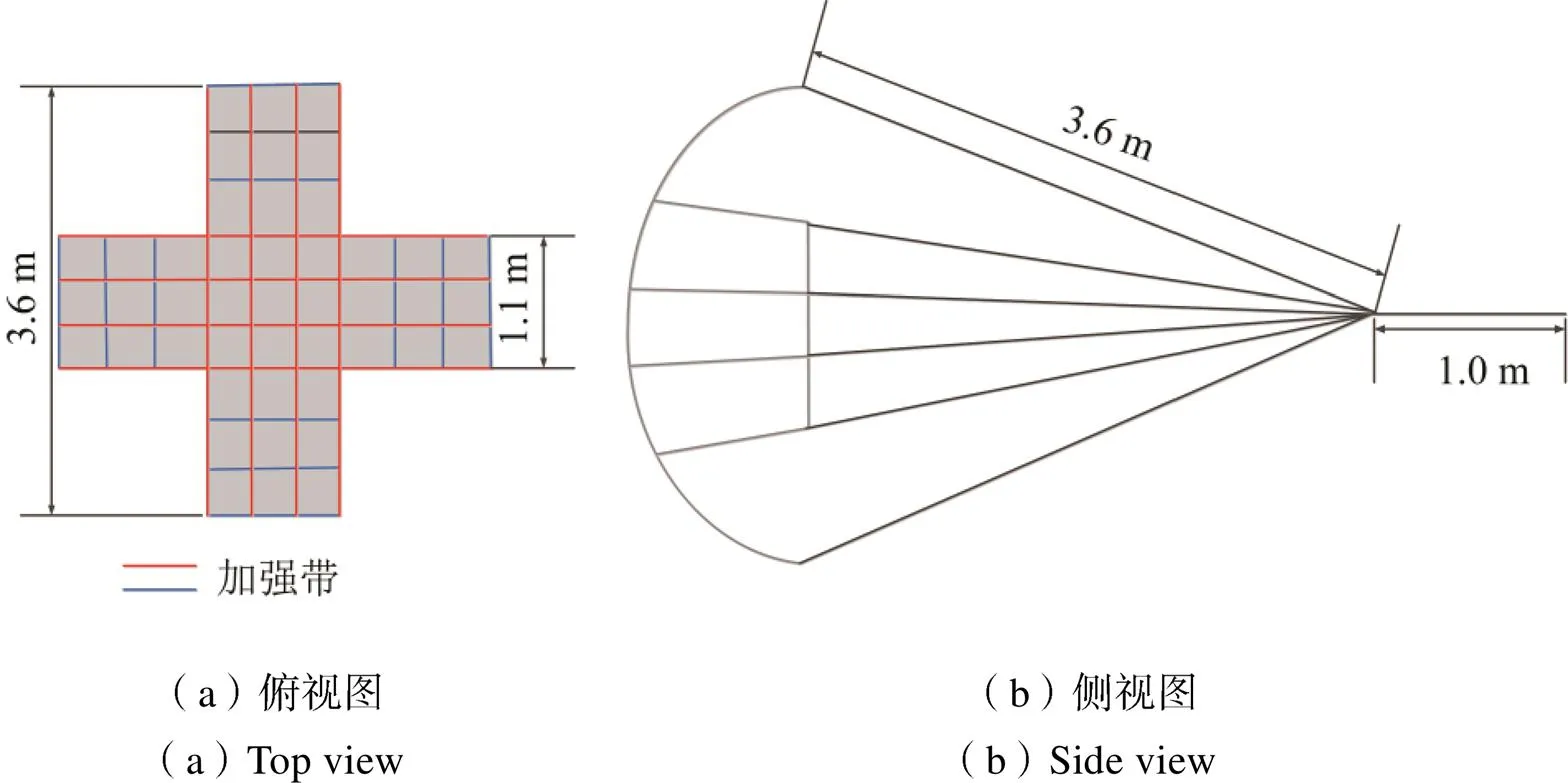
图1 十字形伞外形示意

为降低模型复杂度，作以下基本假设：不考虑前体的影响，连接绳一端为伞绳集束点，另一端固定于流场中；伞衣部分只考虑加强带，其余部件忽略；流场为亚声速不可压缩流场，且为理想气体的稳态定常流动；不考虑伞绳与流场之间的相互耦合；伞衣为各向同性材料。降落伞部件结构参数见表1。

表1 降落伞部件结构参数

Tab.1 Structural parameters of parachute components

2.2 网格划分

2.2.1 降落伞网格

本文通过动力学方法建立降落伞初始模型，如图2所示。首先建立十字形伞平面模型，伞衣为四边形单元，伞绳为线单元（见图2（a））；然后将伞衣中点固定，对连接绳一端施加远离伞衣的位移载荷，在伞绳作用下，降落伞伞衣将以十字形折叠（见图2（b））。为了保证展开后伞绳长度一致，初始时刻部分伞绳呈折线状态。

图2 十字形伞网格模型

2.2.2 流场网格

为了与试验风洞尺寸一致，从而方便与试验结果进行对比，将流场区域设置为六面体，尺寸为18 m×8 m×6 m。流场网格为六面体单元，在降落伞处对网格进行了十字形加密，总单元数为1.7×106个，如图3所示。

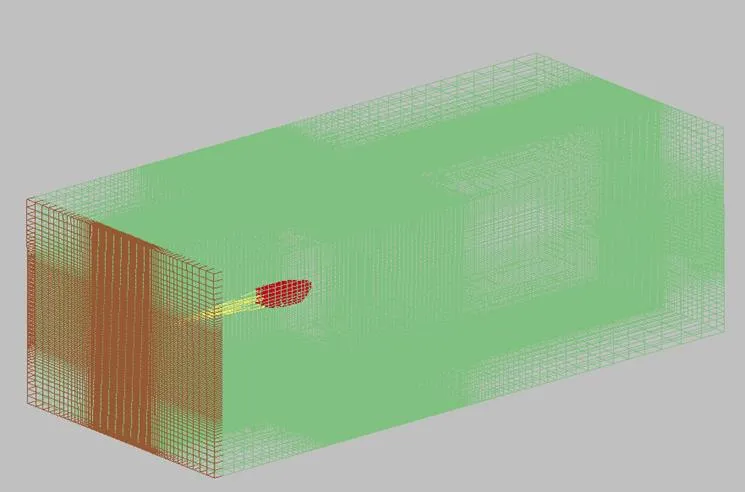
图3 流场网格示意

3 开伞过程仿真

3.1 工况设置

在建立数值计算模型的基础上，为了使仿真计算结果更加接近十字形伞实际工作过程中的状态，同时方便与已有的风洞试验结果进行对比，本文设置以下计算工况：来流速度40 m/s，气体密度1.35 kg/m3，温度258 K；流场除入口外，其余壁面均为无反射边界。此工况下获得的仿真结果具有一定的代表性，可以反映十字形伞开伞充气过程的动力学规律。

3.2 仿真结果分析

3.2.1 稳态外形

十字形伞充气过程结束后进入稳态阶段，截取稳态阶段伞衣状态并与风洞试验照片进行对比，如图4所示，可见稳态阶段仿真所得十字形伞外形与试验所得基本一致，说明本文采用的数学模型及数值方法能够较好地模拟十字形伞实际工作状况，结果具有可靠性。

图4 仿真与风洞试验的稳态伞衣外形对比

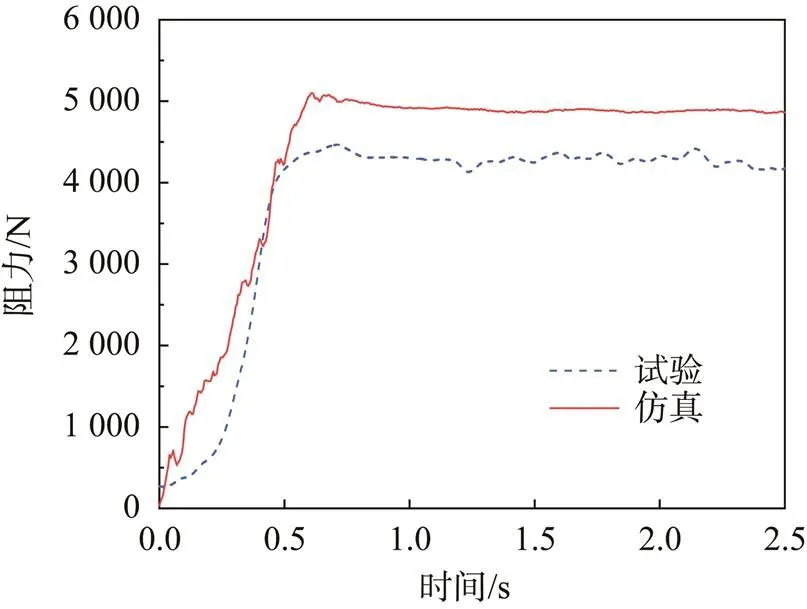
图5 仿真与风洞试验的气动载荷曲线对比

3.2.2 载荷历程

提取连接绳末端所受拉力，以此表征降落伞所受气动载荷。图5为十字形伞开伞过程载荷变化仿真结果与试验结果的对比，由图可知，气动载荷在开伞过程中逐渐增大，达到峰值后略有降低，随后趋于稳定，载荷值在一定范围内波动，仿真结果与试验结果的趋势一致。

定义开伞载荷达到最大值的时刻为开伞过程结束时刻，由图5可得开伞时间仿真结果约为0.66 s，试验结果约为0.72 s，误差为8.3%；降落伞最大载荷仿真结果为5 070 N，试验结果为4 466 N，误差为13.5%；降落伞充气稳定后阻力随时间的平均值仿真结果约为4 868 N，试验结果约为4 278 N，误差为13.8%。仿真获得的3项结果均与试验值存在一定误差，原因可能是仿真中没有考虑湍流的影响，误差均在工程可接受的合理范围内。

3.2.3 伞衣应力

为了分析开伞充气全过程伞衣内的应力变化，在图6中分别展示了充气过程中（=0.47 s）、载荷达到最大值时刻（=0.66 s）及降落伞稳定阶段（=2.0 s）三个不同时刻伞衣的有效应力分布情况。图中红色区域即为应力集中区域，可见无论是充气阶段还是稳定阶段，应力最大点都位于伞衣臂中心附近区域。

图6 不同时刻伞衣应力分布

图7为十字形伞4个伞臂中心点（1～4）有效应力随时间变化的曲线。由图可知，在0.66 s之前即充气过程中，由于4个伞衣臂张开先后顺序不同，4个伞衣臂中心点有效应力虽然均为上升趋势，但并不是同步上升，结合图6（a）可知各伞衣臂的应力分布也不同；在0.66 s时降落伞充气完成，载荷达到最大值，4个伞衣臂中心点的有效应力值几乎同时上升到最大值；0.66 s以后即降落伞稳定后，各伞衣臂中心点的有效应力值在达到最大值后均略有降低并趋于稳定，结合图6（c）可知伞衣应力分布趋于稳定，且呈现对称分布状态。

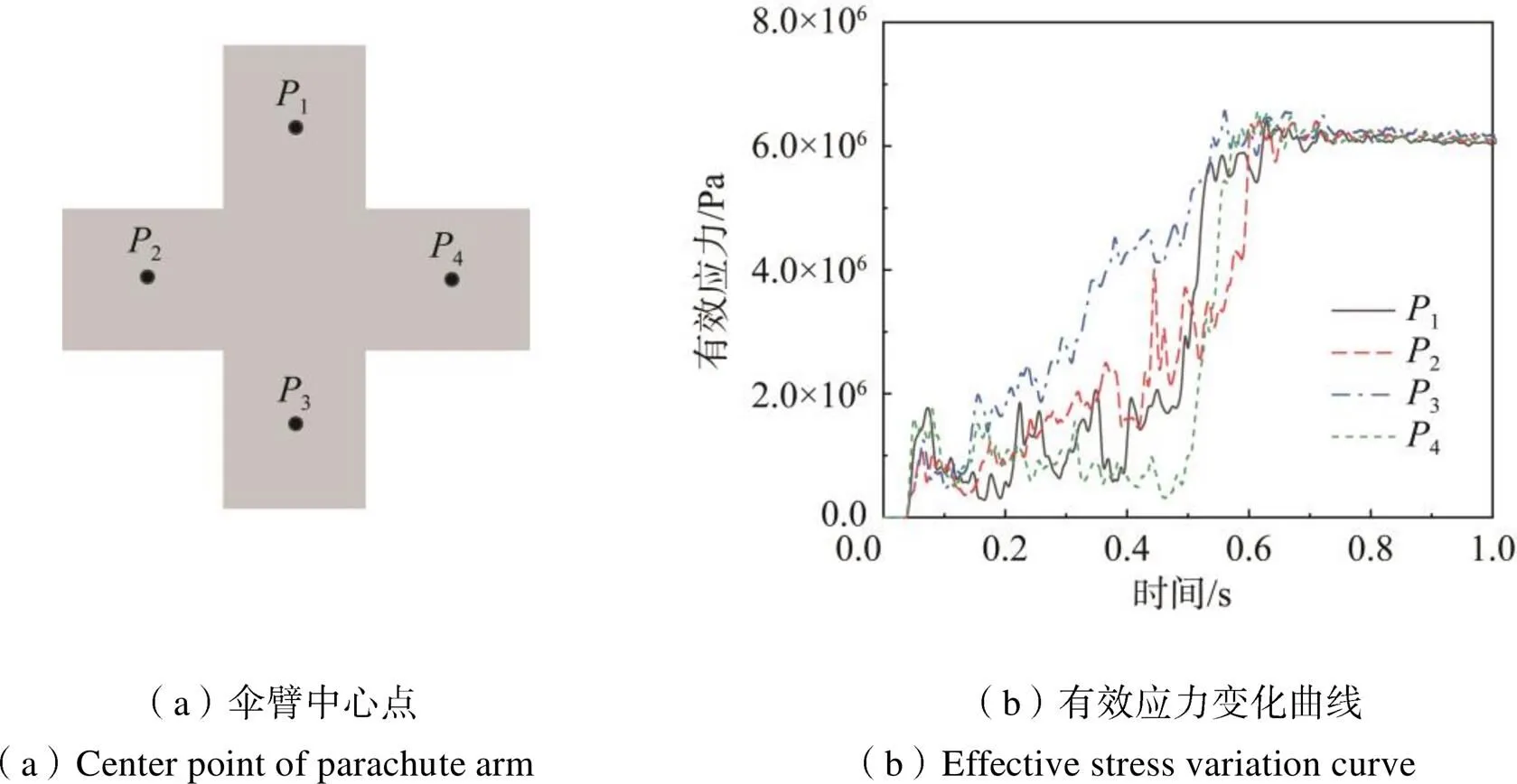
图7 伞臂中心点有效应力变化历程

4 结束语

本文基于流固耦合方法对十字形降落伞开伞充气过程进行了仿真。在本文的计算模型中，通过ALE方法求解流场N-S方程，通过拉格朗日方法求解降落伞结构变形，通过罚函数方法处理流场与降落伞之间的流固耦合及伞衣之间接触。

仿真结果与风洞试验结果进行对比分析，发现十字形伞充气后的稳态外形仿真结果与试验基本一致，且开伞过程中载荷变化曲线与试验结果基本吻合，证明了仿真方法的适用性与准确性。

仿真结果表明，十字形伞伞衣的最大应力点总是位于伞臂的中心位置，但不同伞臂的应力分布受充气先后顺序的影响；在降落伞达到稳定状态后，伞衣的应力分布呈现对称分布。

本文的仿真计算方法可作为试验手段的有效补充。通过对十字形伞伞衣应力分布情况的分析可以认识到开伞过程中存在的应力分布不均现象，有助于避免降落伞因应力集中而发生失稳或破坏，可为十字形伞优化改进提供参考。但是本文的模型未考虑湍流等因素的影响，仿真结果仍然存在一定误差，未来可在本文工作的基础上优化计算模型，以提高仿真的精度。

[1] 王利荣. 降落伞理论及应用[M]. 北京:宇航出版社, 1997: 102-104. WANG Lirong. Parachute Theory and Application[M]. Beijing: China Astronautic Publishing House, 1997:102-104. (in Chinese)

[2] 贾华明, 杨霞, 李少腾, 等. 环帆伞技术与发展综述[J]. 航天返回与遥感, 2021, 42(3): 41-51. JIA Huaming, YANG Xia, LI Shaoteng, et al. Overview of the Technology and Development of Ringsail Parachute[J]. Spacecraft Recovery & Remote Sensing, 2021, 42(3): 41-51. (in Chinese)

[3] 韩雅慧, 杨春信, 肖华军, 等. 十字形伞的实验研究进展及展望[J]. 兵工自动化, 2013, 32(3): 3-8, 20. HAN Yahui, YANG Chunxin, XIAO Huajun, et al. Development History and Expectation of Cross Parachute[J].Ordnance Industry Automation, 2013, 32(3): 3-8, 20. (in Chinese)

[4] 喻东明, 马啸民, 杨品. 亚声速条件下十字形伞充满时间系数的解算方法及仿真验证[J]. 南京航空航天大学学报, 2021, 53(2): 177-181. YU Dongming, MA Xiaomin, YANG Pin. Solution of Inflation Coeffcient of Cruciform Parachute Under Subsonic Conditions and Simulation Verification[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2021, 53(2): 177-181. (in Chinese)

[5] 贾华明, 李健. 收口十字形降落伞充气过程动力学建模与仿真[J]. 航天返回与遥感, 2012, 33(5): 16-23. JIA Huaming, LI Jian.Modeling and Simulation of Inflation Process Dynamics of Reefed Cruciform Parachute [J]. Spacecraft Recovery & Remote Sensing, 2012, 33(5): 16-23. (in Chinese)

[6] 贾贺, 包进进, 荣伟. 设计参数及大气参数对降落伞充气性能的影响[J]. 航天返回与遥感, 2020, 41(3): 28-36. JIA He, BAO Jinjin, RONG Wei. The Design and Atmospheric Parameters Influences on Parachute Inflation Performance[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(3): 28-36. (in Chinese)

[7] 荣伟. 航天器进入下降与着陆技术[M]. 北京: 北京理工大学出版社, 2018 RONG Wei. Spacecraft Entry, Decent and Landing Technology[M]. Beijing: Science Press, 2018. (in Chinese)

[8] 王立武, 房冠辉, 李健, 等. 降落伞超声速低动压高空开伞试验[J]. 航天返回与遥感, 2020, 41(3): 1-9. WANG Liwu, FANG Guanhui, LI Jian, et al. The Experiments of Parachute Deployment at Supersonic and Low Dynamic Pressure Condition[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(3): 1-9. (in Chinese)

[9] 余莉, 明晓, 胡斌. 降落伞开伞过程的试验研究[J]. 南京航空航天大学学报, 2006, 38(2): 176-180. YU Li, MING Xiao, HU Bin.Experimental Investigation in Parachute Opening Process[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2006, 38(2):176-180. (in Chinese)

[10] 余莉, 腾海山, 明晓. 利用七孔探针对降落伞流场的试验测量研究[J]. 南京航空航天大学学报, 2007, 39(5): 65-70. YU Li, TENG Haishan, MING Xiao. Seven-hole Probe Measurement on Parachute Flow Field[J]. Journal of Nanjing University of Aeronautics & Astronautics,2007, 39(5): 65-70. (in Chinese)

[11] CAO Y, NIE S, WU Z. Numerical Simulation of Parachute Inflation: A Methodological Review[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2019, 233(2): 736-766.

[12] 包文龙, 贾贺, 薛晓鹏, 等. 开“窗”结构对环帆伞稳态气动性能的影响[J]. 航天返回与遥感, 2022, 43(1): 1-11. BAO Wenlong, JIA He, XUE Xiaopeng, et al. The Influence of the‘Windows’Structure on the Steady-state Aerodynamic Performance of Ringsail Parachute[J]. Spacecraft Recovery & Remote Sensing, 2022, 43(1): 1-11. (in Chinese)

[13] STEEVES E C, BENNEY R J, STEIN K R. A Computational Model that Couples Aerodynamic and Structural Dynamic Behavior of Parachutes during the Opening Process: NASA-ADA264115[R]. Washingtong DC: NASA, 1993.

[14] STEIN K, BENNEY R, TEZDUYAR T, et al.Fluid-structure Interactions of a Cross Parachute: Numerical Simulation[J]. Computer Methods in Applied Mechanics & Engineering, 2001, 191(6/7):673-687.

[15] KIM Y, PESKIN C S. 3-D Parachute Simulation by the Immersed Boundary Method[J]. Computers & Fluids, 2009, 38(6): 1080-1090.

[16] TUTT B, TAYLOR A. The Use of LS-DYNA to Simulate the Inflation of a Parachute Canopy[C]// 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, May 23-26, 2005, Munich, Germany.

[17] GAO X, ZHANG Q, TANG Q. Numerical Modelling of Mars Supersonic Disk-gap-band Parachute Inflation[J]. Advances in Space Research, 2016, 57(11): 2259-2272.

[18] COQUET Y, BORDENAVE P, CAPMAS G, et al. Improvements in Fluid Structure Interaction Simulations of Parachutes Using LS-Dyna®[C]// 21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, May 23-26, 2011, Dublin, Ireland.

[19] 贾贺, 荣伟, 陈国良. 基于LS-DYNA软件的降落伞充气过程仿真研究[J]. 航天器环境工程, 2010, 27(3): 367-373. JIA He, RONG Wei, CHEN Guoliang. The Simulations of Parachute Inflation Process by Using LS-DYNA[J]. Spacecraft Environment Engineering, 2010, 27(3): 367-373. (in Chinese)

[20] 高兴龙. 基于ALE方法的开缝降落伞充气过程研究[J]. 航天返回与遥感, 2013, 34(1): 13-20. GAO Xinglong. A Study on the Slots-parachute Inflation Based on ALE Method[J].Spacecraft Recovery & Remote Sensing, 2013, 34(1), 13-20. (in Chinese)

[21] ZHAO M, ZHANG S, ZHANG Z, et al. Modeling and Simulation of Supersonic Parachute Inflation in Mars Environment[C]// Proceedings of the 21st International Conference on MMESE, October 23-25, 2021, Beijing, China. Singapore: Springer, 2022: 445-451.

[22] HIRT C W, AMSDEN A A, COOK J L. An Arbitrary Lagrangian–Eulerian Computing Method for All Flow Speeds[J]. Journal of Computational Physics, 1997, 135(2): 203-216.

[23] BENSON D J. Computational Methods in Lagrangian and Eulerian Hydrocodes[J]. Computer Methods in Applied Mechanics & Engineering, 1992, 99(2/3): 235-394.

[24] LINGARD J, UNDERWOOD J. The Effects of Low Density Atmospheres on the Aerodynamic Coefficients of Parachutes[C]// 13th Aerodynamic Decelerator Systems Technology Conference, May15-18, 1995, Clearwater Beach, FL, USA.

Numerical Simulation Study of Cruciform Parachute Deployment and Inflation Process

XIE Huai LIU Yu WANG Zhen CHANG Fei

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

The cruciform parachute is a commonly used parachute design in the field of aerospace deceleration，and the deployment and inflation stage is a complex stage of its operation. In order to study the dynamics characteristics of cruciform parachute deployment and inflation process, this paper employs the arbitrary Lagrangian-Eulerian method to carry out the fluid-structure interactionsimulation calculations on the deployment process of a cruciform parachute. The computed results are compared with wind tunnel test results. The comparison shows that the simulated steady-state shape of the parachute is consistent with the experimental results, and the simulated aerodynamic load history curve of the parachute is largely in agreement with the test results. The load exhibits a gradual increase during the deployment process, reaching its maximum value after the completion of the deployment, followed by a slight decrease and gradual stabilization. The simulation results also show that, during the cruciform parachute deployment process, the maximum stress point of the canopy is located in the central region of the canopy arms, and the inflation sequence affects the stress distribution along the arms. After the parachute stabilizes, the canopy stress exhibits a symmetrical distribution. The simulation method employed in this study effectively simulates the dynamic process of cruciform parachute deployment and inflation, and the characteristics of canopy stress distribution and influencing factors can provide valuable insights for the design and optimization of cruciform parachutes.

cruciform parachute; fluid-structure interaction (FSI); deployment; inflation

V445

A

1009-8518(2023)03-0032-09

10.3969/j.issn.1009-8518.2023.03.004

谢淮，男，1976年生，2006年获国防科技大学管理科学与工程专业硕士学位，高级工程师。主要研究方向为航天器进入、减速与着陆技术。E-mail：xh7603@hotmail.com。

2023-01-06

工业和信息化部重点实验室开放基金（KLAECLS-E-202004）

谢淮, 刘宇, 王臻, 等. 十字形伞开伞充气过程数值仿真研究[J]. 航天返回与遥感, 2023, 44(3): 32-40.

XIE Huai, LIU Yu, WANG Zhen, et al. Numerical Simulation Study of Cruciform Parachute Deployment and Inflation Process[J]. Spacecraft Recovery & Remote Sensing, 2023, 44(3): 32-40. (in Chinese)

（编辑：陈艳霞）